文档内容
武汉市 2024 届部分学校高三年级九月调研考试
数学试卷参考答案及评分标准
选择题:
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B C D B A C C B ABD BC AD ACD
填空题:
13. − 4 0 14. (x+1)2+(y−2)2 =5 15. 4−2ln2 16.(1)
12 14
;(2)
19
[ 4 − ( −
12
) n ]
解答题:
17.(10分)解:
(1)由题意, 2 S
n
= ( n + 2 ) ( a
n
− 1 ) , 2 S
n + 1
= ( n + 3 ) ( a
n + 1
− 1 ) .
两式相减得: 2 a
n + 1
= ( n + 3 ) a
n + 1
− ( n + 2 ) a
n
− 1 ,
即(n+1)a =(n+2)a +1.
n+1 n
此时
a
n
n+ + 12 =
n
a
n+
1
+
( n + 1
1)
( n + 2 )
,
a a 1 1
即 n+1 = n + − .
n+2 n+1 n+1 n+2
a +1 a +1
有 n+1 = n ,所以数列
n+2 n+1
{
a
n
n
+
+
1
1
} 是常数列. …………5分
(2)取 n = 1 ,有 2 a
1
= 3 ( a
1
− 1 ) ,解得 a
1
= 3 .
a +1 a +1
由(1)可得: n = 1 =2,所以
n+1 1+1
a
n
= 2 n + 1 .
a
n
1a
n + 1
=
( 2 n + 1
1)
( 2 n + 3 )
=
12
(
2 n
1
+ 1
−
2 n
1
+ 3
) .
所以 T
n
=
12
(
13
−
15
+
15
−
17
+ . .. +
2 n
1
+ 1
−
2 n
1
+ 3
) =
12
(
13
−
2 n
1
+ 3
) =
6 n
n+
9
. …………10分
18.(12分)解:
(1)由正弦定理得:2sinAcosB=2sinC−sinB.
2sinAcosB=2sin(A+B)−sinB,
2 s i n A c o s B = 2 s i n A c o s B + 2 c o s A s i n B − s i n B ,即2cosAsinB=sinB.
又 s i n B 0
1
,故cosA= .
2
所以A= . …………6分
3
(2)ABC面积 S =
12
b c s i n A =
12
( a + b + c ) r .
代入 a = 7
和A= ,整理得:
3
b c = 2 ( b + c ) + 1 4 .①
由余弦定理: a 2 = b 2 + c 2 − 2 b c c o s A ,得:b2+c2−bc=49.
bc−14
即(b+c)2 −3bc=49,代入①,得:( )2 −3bc=49.
2
解得:bc=40.
1
所以S = bcsinA=10 3. …………12分
219.(12分)解:
(1)由题意,第一组的频率/组距为:
1
10
− m − 0 .0 4 − 0 .0 2 5 − 0 .0 1 = 0 .0 2 5 − m .
样本平均数的估计值为: 1 0 [ ( 0 .0 2 5 − m ) 5 5 + m 6 5 + 0 .0 4 7 5 + 0 .0 2 5 8 5 + 0 .0 1 9 5 ] = 7 4 .5 + 1 0 0 m .
样本中位数的估计值为: 7 0 + 1 0
0 . 0 5
0
−.
0
04 . 0 2 5
= 7 6 . 2 5 .
所以 7 4 . 5 + 1 0 0 m = 7 6 . 2 5 ,解得: m = 0 . 0 1 7 5 . …………6分
(2)总的成绩优秀人数为: 2 0 0 1 0 ( 0 .0 2 5 + 0 .0 1 ) = 7 0 .
得到列联表为:
测试成绩
性别 合计
优秀 不优秀
男生 45 65 110
女生 25 65 90
合计 70 130 200
χ 2 =
2 0 01 1 (0 4 5 9
0
6 5
7
−0 2 51 3 60 5 ) 2
=
2 66 09 03
3 . 7 5 3 . 8 4 1 .
所以根据小概率值 0 . 0 5 = 的独立性检验,认为男生和女生的优秀率没有差异. …………12分
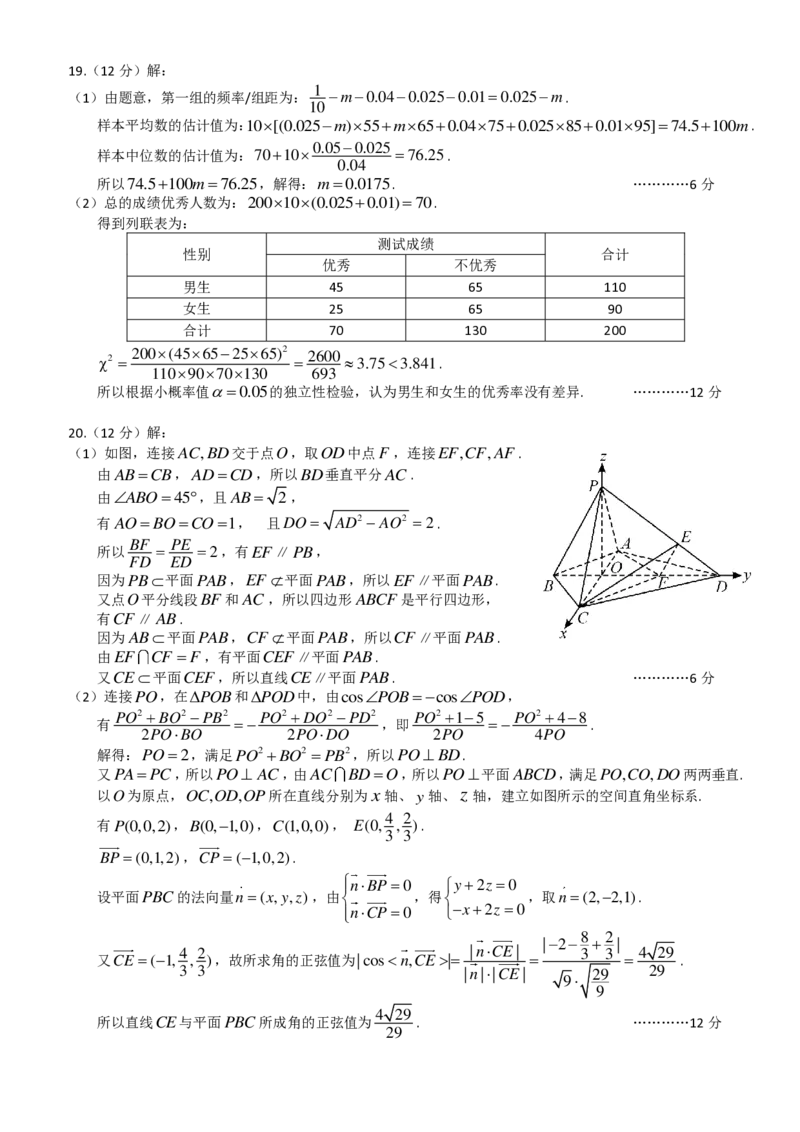
20.(12分)解:
(1)如图,连接 A C , B D 交于点 O ,取 O D 中点 F ,连接 E F , C F , A F .
由 A B = C B , A D = C D ,所以 B D 垂直平分 A C .
由ABO=45,且AB= 2,
有 A O = B O = C O = 1 , 且DO= AD2 −AO2 =2.
所以
BF FD
=
PE ED
= 2 ,有EF∥ P B ,
因为 P B 平面 P A B , E F 平面 P A B ,所以EF∥平面 P A B .
又点 O 平分线段 B F 和 A C ,所以四边形 A B C F 是平行四边形,
有 C F ∥AB.
因为 A B 平面 P A B , C F 平面 P A B ,所以 C F ∥平面 P A B .
由EF CF =F,有平面 C E F ∥平面 P A B .
又CE平面 C E F ,所以直线 C E ∥平面 P A B . …………6分
(2)连接PO,在POB和POD中,由 c o s P O B = − c o s P O D ,
PO2 +BO2 −PB2 PO2 +DO2 −PD2 PO2 +1−5 PO2 +4−8
有 =− ,即 =− .
2POBO 2PODO 2PO 4PO
解得:PO=2,满足PO2 +BO2 =PB2,所以 P O ⊥ B D .
又 P A = P C ,所以 P O ⊥ A C ,由 A C B D = O ,所以PO⊥平面ABCD,满足 P O , C O , D O 两两垂直.
以O为原点,OC,OD,OP所在直线分别为 x 轴、 y 轴、z 轴,建立如图所示的空间直角坐标系.
有P(0,0,2), B ( 0 , − 1 , 0 ) , C ( 1 , 0 , 0 ) , E ( 0 ,
43
,
23
) .
B P = ( 0 , 1 , 2 ) , C P = ( − 1 , 0 , 2 ) .
设平面PBC的法向量n=(x,y,z),由
n
n
B
C
P
P
=
=
0
0
y+2z =0
,得 ,取n=(2,−2,1).
−x+2z =0
8 2
|−2− + |
4 2 |nCE| 3 3 4 29
又CE =(−1, , ),故所求角的正弦值为|cosn,CE |= = = .
3 3 |n||CE| 29 29
9
9
4 29
所以直线CE与平面PBC所成角的正弦值为 . …………12分
2921.(12分)解:
(1)由题意, | A B |= 2 a = 4 ,得: a = 2 .
a2 −b2 3
离心率e= = ,得:
a 2
b = 1 .
所以椭圆 E 的标准方程为
x4 2
+ y 2 = 1 . …………3分
(2)设 C ( x
C
, y
C
) , D ( x
D
, y
D
) .
点 A ( − 2 , 0 ) ,直线 A T
1 1
的方程为y = (x+2),即
2 t+2
x = 2 ( t + 2 ) y − 2 .
与椭圆方程联立得: ( t 2 + 4 t + 5 ) y 2 − 2 ( t + 2 ) y = 0 ,解得: y
C
=
t
22 (
+
t +
4 t
2
+
)
5
.
点B(2,0),直线 B T 的方程为x=2(t−2)y+2.
与椭圆方程联立得: ( t 2 − 4 t + 5 ) y 2 + 2 ( t − 2 ) y = 0
−2(t−2)
,解得:y = .
D t2 −4t+5
三角形面积比
S
S
C
A
D
B
T
T
=
1212
| C
| A
T
T
| |
| |
D
B
T
T
|
|
s
s
i n
i n
C
A
T
T
D
B
=
|| CA TT ||
|| DB TT ||
=
y
C
12
−
−
12
0
y
D
12
−
−
12
0
= ( 2 y
C
− 1 ) ( 2 y
D
− 1 )
又因为 S
A B T
=
12
4
12
= 1 ,
所以 S
C D T
= ( 2 y
C
− 1 ) ( 2 y
D
− 1 ) = (
t 2
4+ t +4
t
8+
5
− 1 ) (
t
−2 4− t4 +t 8+
5
− 1 ) =
( t 2
(
+
t 2
5
−
) 2
3
−
) 2
1 6 t 2
.
由题意,
( t 2
(
+
t 2
5
−
) 2
3
−
) 2
1 6 t 2
=
1
17
,整理得t4 −6t2 +8=0,解得:t2 =2或t2 =4.
又由点T 在椭圆内部,故 t 2 = 2 ,即 t = 2 . …………12分
22.(12分)解:
(1) m = n = 0 时, f ( x ) = x 2 e x .
f '( x ) = ( x 2 + 2 x ) e x = x ( x + 2 ) e x .
令 f '( x ) = 0 ,得 x = − 2 或x=0.
当x−2或 x 0 时, f '( x ) 0 , f ( x ) 单调递增;
当 − 2 x 0 时, f '( x ) 0 , f(x)单调递减.
综上所述: f ( x ) 在 ( − , − 2 ) 和 ( 0 , + ) 上单调递增,在 ( − 2 , 0 ) 单调递减. …………5分
(2) f '(x)=[x2 +(m+2)x+m+n]ex.
令 f '(x)=0,得 x 2 + ( m + 2 ) x + m + n = 0 .
由题意, x
1
, x
2
是关于x的方程 x 2 + ( m + 2 ) x + m + n = 0 的两个实根.
所以 x
1
+ x
2
= − ( m + 2 ) ,x x =m+n.
1 2
由x2 +(m+2)x +m+n=0,有
1 1
x
1
2 = − ( m + 2 ) x
1
− m − n .
所以 f ( x
1
) = ( x
1
2 + m x
1
+ n ) e x1 = ( − 2 x
1
− m ) e x1 ,将m=−x −x −2代入,
1 2
得 f(x )=(x −x +2)ex 1,同理可得: f(x )=(x −x +2)ex 2 .
1 2 1 2 1 2
f(x )− f(x ) (x −x +2)ex 2 −(x −x +2)ex 1 (x −x −2)ex 2 −x 1 +(x −x +2)
所以 2 1 = 1 2 2 1 =− 2 1 2 1 .
ex 2 −ex 1 ex 2 −ex 1 ex 2 −x 1 −1令x −x =t(t 0),上式为
2 1
−
( t − 2 ) e
e
t
t
+
− 1
( t + 2 )
.
(t−2)et +(t+2)
设g(t)=− (t 0),此时
et −1
g ( t ) = −
t ( e
e
t
t
+
−
1
1
)
+ 2 .
g '( t ) = −
e 2 t
(
−e
t
2− t e1 t
)
−2 1
.
记 h ( t ) = e 2 t − 2 t e t − 1 , h '( t ) = 2 e t ( e t − t − 1 ) .
记(t)=et −t−1, t 0 时, '( t ) e t 1 0 = − , ( t ) 单调递增,所以 ( t ) ( 0 ) 0 = .
所以h'(t)0,h(t)单调递增,h(t)h(0)=0.
所以 g '( t ) 0 , g ( t ) 在 ( 0 , + ) 单调递减.
又 t 2 = ( x
2
− x
1
) 2 = ( x
2
+ x
1
) 2 − 4 x
1
x
2
= m 2 − 4 n + 4 .
此时 t 2 = ( a + b + 2 ) 2 − 4 ( a 2 + b 2 + 2 ) + 4 = − 3 a 2 − 3 b 2 + 2 a b + 4 a + 4 b .
t 2 = − 3 a 2 + ( 2 b + 4 ) a − 3 b 2 + 4 b = − 3 ( a −
b +3 2
) 2 −
83
b 2 +
1 63
b +
43
−
83
b 2 +
1 63
b +
43
= −
83
( b − 1 ) 2 + 4 4 .
当且仅当 a −
b +3 2
= 0 且 b − 1 = 0 ,即 a = b = 1 时,t2取到最大值 4 ,即t的最大值为2.
所以
f ( x
e
2x
)
2
−
−
f
e
(
x1
x
1
) −4
的最小值为g(2)= . …………12分
e2 −1