文档内容
专题 13 立体几何的空间角与空间距离
及其综合应用小题综合
考点 十年考情(2015-2024) 命题趋势
考点1 异面直
2022·全国新Ⅰ卷、2021·全国乙卷、2018·全国
线所成角及其
卷
应用
2017·全国卷、2016·全国卷、2015·浙江卷
(10年6考)
2024·全国新Ⅱ卷、2023·全国乙卷、2022·浙江
考点2 线面角 卷
要熟练掌握几何法和向量法求解
及其应用 2022·全国甲卷、2022·全国新Ⅰ卷、2018·浙江
空间角与空间距离,本节内容是
(10年4考) 卷
新高考卷的常考内容,要熟练掌
2018·全国卷、2018·全国卷、2018·全国卷
握方程思想求值,需强化巩固复
2023·北京卷、2023·全国乙卷、2023·全国新Ⅱ
考点3 二面角 习.
卷
及其应用
2022·浙江卷、2019·浙江卷、2018·浙江卷
(10年6考)
2017·浙江卷、2015·浙江卷
考点4 点面距
及其应用 2019·全国卷
(10年1考)
考点01 异面直线所成角及其应用
1.(2022·全国新Ⅰ卷·高考真题)(多选)已知正方体 ,则( )
A.直线 与 所成的角为 B.直线 与 所成的角为
C.直线 与平面 所成的角为 D.直线 与平面ABCD所成的角为
【答案】ABD
【分析】数形结合,依次对所给选项进行判断即可.【详解】如图,连接 、 ,因为 ,所以直线 与 所成的角即为直线 与 所成
的角,
因为四边形 为正方形,则 ,故直线 与 所成的角为 ,A正确;
连接 ,因为 平面 , 平面 ,则 ,
因为 , ,所以 平面 ,
又 平面 ,所以 ,故B正确;
连接 ,设 ,连接 ,
因为 平面 , 平面 ,则 ,
因为 , ,所以 平面 ,
所以 为直线 与平面 所成的角,
设正方体棱长为 ,则 , , ,
所以,直线 与平面 所成的角为 ,故C错误;
因为 平面 ,所以 为直线 与平面 所成的角,易得 ,故D正确.
故选:ABD
2.(2021·全国乙卷·高考真题)在正方体 中,P为 的中点,则直线 与 所成的
角为( )
A. B. C. D.
【答案】D
【分析】平移直线 至 ,将直线 与 所成的角转化为 与 所成的角,解三角形即可.【详解】
如图,连接 ,因为 ∥ ,
所以 或其补角为直线 与 所成的角,
因为 平面 ,所以 ,又 , ,
所以 平面 ,所以 ,
设正方体棱长为2,则 ,
,所以 .
故选:D
3.(2018·全国·高考真题)在正方体 中, 为棱 的中点,则异面直线 与 所成
角的正切值为
A. B. C. D.
【答案】C
【分析】利用正方体 中, ,将问题转化为求共面直线 与 所成角的正切值,
在 中进行计算即可.
【详解】在正方体 中, ,所以异面直线 与 所成角为 ,
设正方体边长为 ,则由 为棱 的中点,可得 ,所以 ,
则 .故选C.
【点睛】求异面直线所成角主要有以下两种方法:(1)几何法:①平移两直线中的一条或两条,到一个平面中;②利用边角关系,找到(或构造)所求角
所在的三角形;③求出三边或三边比例关系,用余弦定理求角;
(2)向量法:①求两直线的方向向量;②求两向量夹角的余弦;③因为直线夹角为锐角,所以②对应的
余弦取绝对值即为直线所成角的余弦值.
4.(2017·全国·高考真题)已知直三棱柱 中, , , ,则异
面直线 与 所成角的余弦值为
A. B. C. D.
【答案】C
【详解】如图所示,补成直四棱柱 ,
则所求角为 ,
易得 ,因此 ,故选C.
平移法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面问题化归为共面问题
来解决,具体步骤如下:
①平移:平移异面直线中的一条或两条,作出异面直线所成的角;
②认定:证明作出的角就是所求异面直线所成的角;
③计算:求该角的值,常利用解三角形;
④取舍:由异面直线所成的角的取值范围是 ,当所作的角为钝角时,应取它的补角作为两条异
面直线所成的角.求异面直线所成的角要特别注意异面直线之间所成角的范围.
5.(2016·全国·高考真题)平面 过正方体ABCD—A B C D 的顶点A, ,
1 1 1 1
, ,则m,n所成角的正弦值为
A. B. C. D.
【答案】A
【详解】试题分析:如图,设平面 平面 = ,平面 平面 = ,因为 平面
,所以 ,则 所成的角等于 所成的角.延长 ,过 作 ,连接
,则 为 ,同理 为 ,而 ,则 所成的角即为 所成的角,
即为 ,故 所成角的正弦值为 ,选A.【点睛】求解本题的关键是作出异面直线所成的角,求异面直线所成角的步骤是:平移定角、连线成形、解
形求角、得钝求补.
6.(2015·浙江·高考真题)如图,三棱锥 中, ,点 分
别是 的中点,则异面直线 所成的角的余弦值是 .
【答案】
【详解】如下图,连结 ,取 中点 ,连结 , ,则可知 即为异面直
线 , 所成角(或其补角)易得 ,
, ,
∴ ,即异面直线 , 所成角的余弦值为 .
考点:异面直线的夹角.考点02 线面角及其应用
1.(2024·全国新Ⅱ卷·高考真题)已知正三棱台 的体积为 , , ,则 与
平面ABC所成角的正切值为( )
A. B.1 C.2 D.3
【答案】B
【分析】解法一:根据台体的体积公式可得三棱台的高 ,做辅助线,结合正三棱台的结构特征求
得 ,进而根据线面夹角的定义分析求解;解法二:将正三棱台 补成正三棱锥
, 与平面ABC所成角即为 与平面ABC所成角,根据比例关系可得 ,进而可求正
三棱锥 的高,即可得结果.
【详解】解法一:分别取 的中点 ,则 ,
可知 ,
设正三棱台 的为 ,
则 ,解得 ,
如图,分别过 作底面垂线,垂足为 ,设 ,
则 , ,
可得 ,
结合等腰梯形 可得 ,
即 ,解得 ,
所以 与平面ABC所成角的正切值为 ;解法二:将正三棱台 补成正三棱锥 ,
则 与平面ABC所成角即为 与平面ABC所成角,
因为 ,则 ,
可知 ,则 ,
设正三棱锥 的高为 ,则 ,解得 ,
取底面ABC的中心为 ,则 底面ABC,且 ,
所以 与平面ABC所成角的正切值 .
故选:B.
2.(2023·全国乙卷·高考真题)已知 为等腰直角三角形,AB为斜边, 为等边三角形,若二
面角 为 ,则直线CD与平面ABC所成角的正切值为( )
A. B. C. D.
【答案】C
【分析】根据给定条件,推导确定线面角,再利用余弦定理、正弦定理求解作答.
【详解】取 的中点 ,连接 ,因为 是等腰直角三角形,且 为斜边,则有 ,
又 是等边三角形,则 ,从而 为二面角 的平面角,即 ,
显然 平面 ,于是 平面 ,又 平面 ,
因此平面 平面 ,显然平面 平面 ,直线 平面 ,则直线 在平面 内的射影为直线 ,
从而 为直线 与平面 所成的角,令 ,则 ,在 中,由余弦定理得:
,
由正弦定理得 ,即 ,
显然 是锐角, ,
所以直线 与平面 所成的角的正切为 .
故选:C
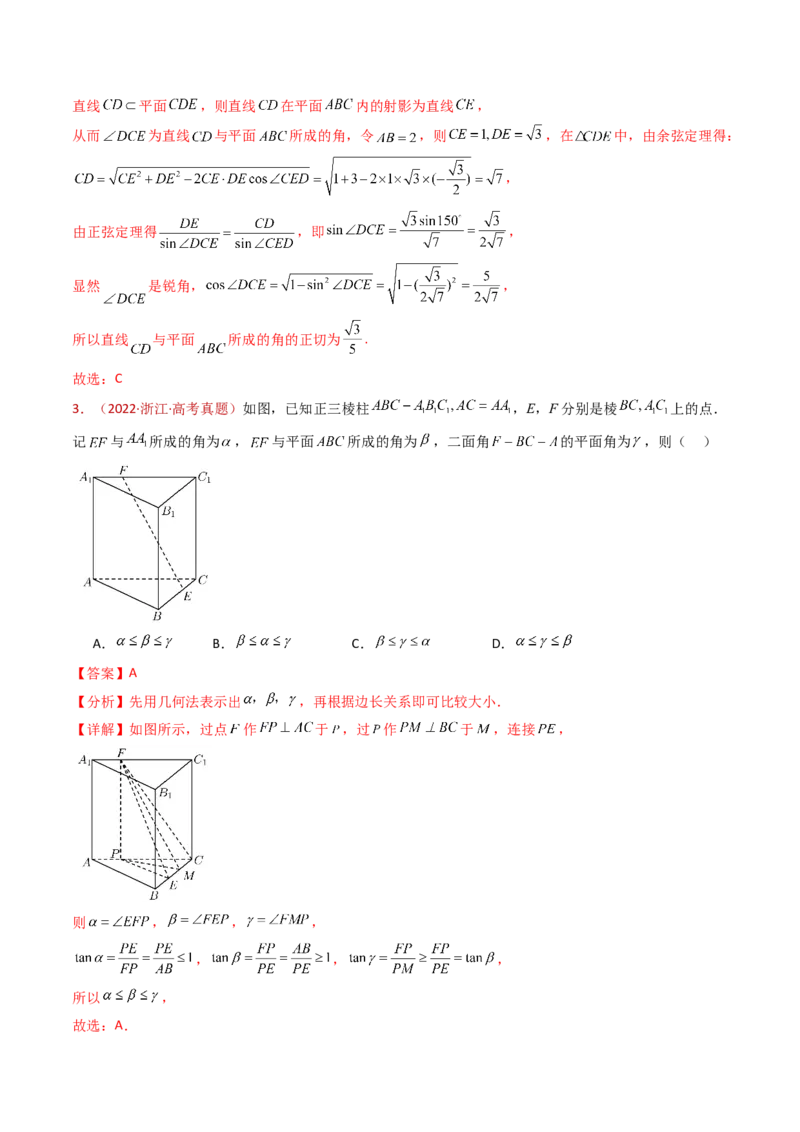
3.(2022·浙江·高考真题)如图,已知正三棱柱 ,E,F分别是棱 上的点.
记 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角为 ,则( )
A. B. C. D.
【答案】A
【分析】先用几何法表示出 ,再根据边长关系即可比较大小.
【详解】如图所示,过点 作 于 ,过 作 于 ,连接 ,
则 , , ,
, , ,
所以 ,
故选:A.4.(2022·全国甲卷·高考真题)在长方体 中,已知 与平面 和平面 所成
的角均为 ,则( )
A. B.AB与平面 所成的角为
C. D. 与平面 所成的角为
【答案】D
【分析】根据线面角的定义以及长方体的结构特征即可求出.
【详解】如图所示:
不妨设 ,依题以及长方体的结构特征可知, 与平面 所成角为 ,
与平面 所成角为 ,所以 ,即 , ,解得
.
对于A, , , ,A错误;
对于B,过 作 于 ,易知 平面 ,所以 与平面 所成角为 ,因为
,所以 ,B错误;
对于C, , , ,C错误;
对于D, 与平面 所成角为 , ,而 ,所以
.D正确.
故选:D.
5.(2022·全国新Ⅰ卷·高考真题)已知正方体 ,则( )
A.直线 与 所成的角为 B.直线 与 所成的角为
C.直线 与平面 所成的角为 D.直线 与平面ABCD所成的角为
【答案】ABD
【分析】数形结合,依次对所给选项进行判断即可.【详解】如图,连接 、 ,因为 ,所以直线 与 所成的角即为直线 与 所成
的角,
因为四边形 为正方形,则 ,故直线 与 所成的角为 ,A正确;
连接 ,因为 平面 , 平面 ,则 ,
因为 , ,所以 平面 ,
又 平面 ,所以 ,故B正确;
连接 ,设 ,连接 ,
因为 平面 , 平面 ,则 ,
因为 , ,所以 平面 ,
所以 为直线 与平面 所成的角,
设正方体棱长为 ,则 , , ,
所以,直线 与平面 所成的角为 ,故C错误;
因为 平面 ,所以 为直线 与平面 所成的角,易得 ,故D正确.
故选:ABD
6.(2018·浙江·高考真题)已知四棱锥 的底面是正方形,侧棱长均相等, 是线段 上的点
(不含端点),设 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角
为 ,则
A. B. C. D.
【答案】D
【分析】分别作出线线角、线面角以及二面角,再构造直角三角形,根据边的大小关系确定角的大小关系.
【详解】设 为正方形 的中心, 为 中点,过 作 的平行线 ,交 于 ,过 作
垂直 于 ,连接 、 、 ,则 垂直于底面 , 垂直于 ,
因此从而
因为 ,所以 即 ,选D.
【点睛】线线角找平行,线面角找垂直,面面角找垂面.
7.(2018·全国·高考真题)已知圆锥的顶点为 ,母线 , 所成角的余弦值为 , 与圆锥底面所成
角为45°,若 的面积为 ,则该圆锥的侧面积为 .
【答案】
【分析】先根据三角形面积公式求出母线长,再根据母线与底面所成角得底面半径,最后根据圆锥侧面积公
式求出结果.
【详解】因为母线 , 所成角的余弦值为 ,所以母线 , 所成角的正弦值为 ,因为
的面积为 ,设母线长为 所以 ,
因为 与圆锥底面所成角为45°,所以底面半径为 ,
因此圆锥的侧面积为 .
【整体点评】根据三角形面积公式先求出母线长,再根据线面角求出底面半径,最后根据圆锥侧面积公式
求出侧面积,思路直接自然,是该题的最优解.
8.(2018·全国·高考真题)在长方体 中, , 与平面 所成的角为
,则该长方体的体积为
A. B. C. D.
【答案】C
【分析】首先画出长方体 ,利用题中条件,得到 ,根据 ,求得
,可以确定 ,之后利用长方体的体积公式求出长方体的体积.
【详解】在长方体 中,连接 ,根据线面角的定义可知 ,
因为 ,所以 ,从而求得 ,
所以该长方体的体积为 ,故选C.
【点睛】该题考查的是长方体的体积的求解问题,在解题的过程中,需要明确长方体的体积公式为长宽高
的乘积,而题中的条件只有两个值,所以利用题中的条件求解另一条边的长就显得尤为重要,此时就需要
明确线面角的定义,从而得到量之间的关系,从而求得结果.
9.(2018·全国·高考真题)已知正方体的棱长为1,每条棱所在直线与平面 所成的角都相等,则 截此
正方体所得截面面积的最大值为
A. B. C. D.
【答案】A
【分析】首先利用正方体的棱是3组每组有互相平行的4条棱,所以与12条棱所成角相等,只需与从同一
个顶点出发的三条棱所成角相等即可,从而判断出面的位置,截正方体所得的截面为一个正六边形,且边
长是面的对角线的一半,应用面积公式求得结果.
【详解】根据相互平行的直线与平面所成的角是相等的,
所以在正方体 中,
平面 与线 所成的角是相等的,
所以平面 与正方体的每条棱所在的直线所成角都是相等的,
同理平面 也满足与正方体的每条棱所在的直线所成角都是相等,
要求截面面积最大,则截面的位置为夹在两个面 与 中间的,
且过棱的中点的正六边形,且边长为 ,
所以其面积为 ,故选A.
点睛:该题考查的是有关平面被正方体所截得的截面多边形的面积问题,首要任务是需要先确定截面的位
置,之后需要从题的条件中找寻相关的字眼,从而得到其为过六条棱的中点的正六边形,利用六边形的面
积的求法,应用相关的公式求得结果.考点03 二面角及其应用
1.(2023·北京·高考真题)坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以勾勒
出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两个面
是全等的等腰三角形.若 ,且等腰梯形所在的平面、等腰三角形所在的平面与平
面 的夹角的正切值均为 ,则该五面体的所有棱长之和为( )
A. B.
C. D.
【答案】C
【分析】先根据线面角的定义求得 ,从而依次求 , , , ,再把所
有棱长相加即可得解.
【详解】如图,过 做 平面 ,垂足为 ,过 分别做 , ,垂足分别为 ,
,连接 ,
由题意得等腰梯形所在的面、等腰三角形所在的面与底面夹角分别为 和 ,
所以 .
因为 平面 , 平面 ,所以 ,
因为 , 平面 , ,
所以 平面 ,因为 平面 ,所以 ,.
同理: ,又 ,故四边形 是矩形,
所以由 得 ,所以 ,所以 ,
所以在直角三角形 中,
在直角三角形 中, , ,又因为 ,
所有棱长之和为 .
故选:C
2.(2023·全国乙卷·高考真题)已知 为等腰直角三角形,AB为斜边, 为等边三角形,若二
面角 为 ,则直线CD与平面ABC所成角的正切值为( )
A. B. C. D.
【答案】C
【分析】根据给定条件,推导确定线面角,再利用余弦定理、正弦定理求解作答.
【详解】取 的中点 ,连接 ,因为 是等腰直角三角形,且 为斜边,则有 ,
又 是等边三角形,则 ,从而 为二面角 的平面角,即 ,
显然 平面 ,于是 平面 ,又 平面 ,
因此平面 平面 ,显然平面 平面 ,
直线 平面 ,则直线 在平面 内的射影为直线 ,
从而 为直线 与平面 所成的角,令 ,则 ,在 中,由余弦定理得:
,
由正弦定理得 ,即 ,
显然 是锐角, ,
所以直线 与平面 所成的角的正切为 .
故选:C
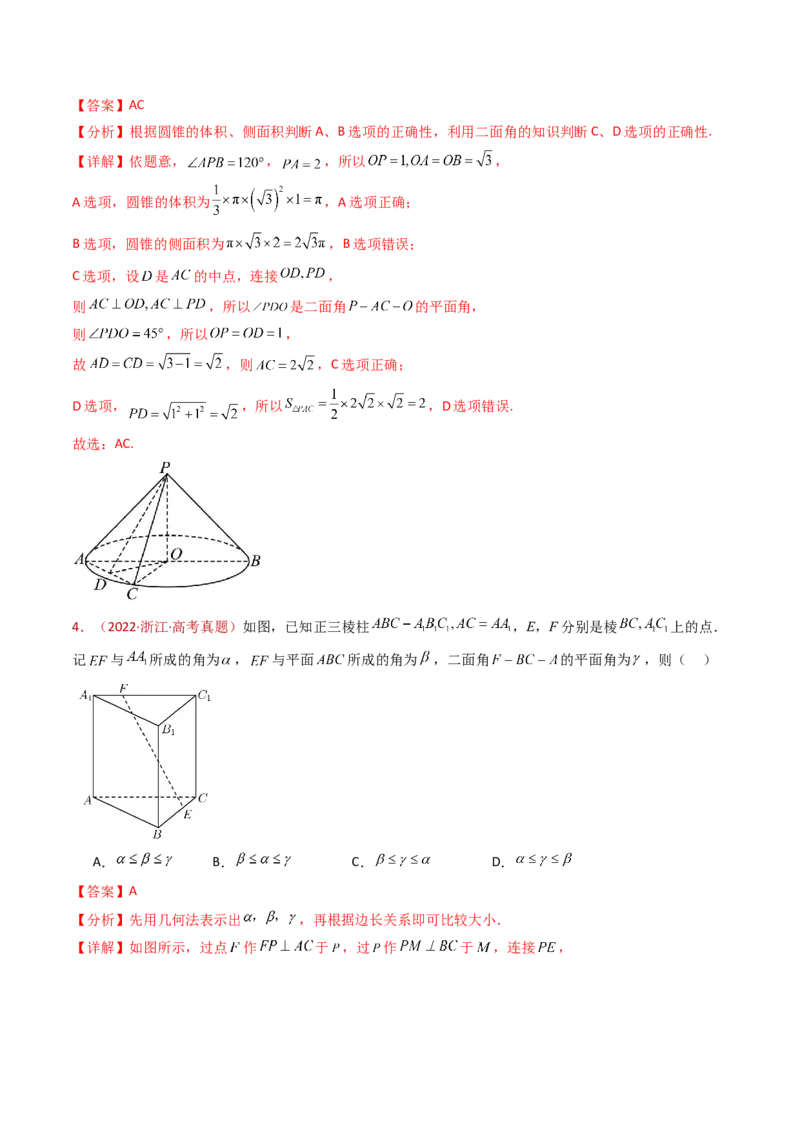
3.(2023·全国新Ⅱ卷·高考真题)(多选)已知圆锥的顶点为P,底面圆心为O,AB为底面直径,
, ,点C在底面圆周上,且二面角 为45°,则( ).
A.该圆锥的体积为 B.该圆锥的侧面积为
C. D. 的面积为【答案】AC
【分析】根据圆锥的体积、侧面积判断A、B选项的正确性,利用二面角的知识判断C、D选项的正确性.
【详解】依题意, , ,所以 ,
A选项,圆锥的体积为 ,A选项正确;
B选项,圆锥的侧面积为 ,B选项错误;
C选项,设 是 的中点,连接 ,
则 ,所以 是二面角 的平面角,
则 ,所以 ,
故 ,则 ,C选项正确;
D选项, ,所以 ,D选项错误.
故选:AC.
4.(2022·浙江·高考真题)如图,已知正三棱柱 ,E,F分别是棱 上的点.
记 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角为 ,则( )
A. B. C. D.
【答案】A
【分析】先用几何法表示出 ,再根据边长关系即可比较大小.
【详解】如图所示,过点 作 于 ,过 作 于 ,连接 ,则 , , ,
, , ,
所以 ,
故选:A.
5.(2019·浙江·高考真题)设三棱锥 的底面是正三角形,侧棱长均相等, 是棱 上的点(不含
端点),记直线 与直线 所成角为 ,直线 与平面 所成角为 ,二面角 的平面角
为 ,则
A. B.
C. D.
【答案】B
【解析】本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及
各种角的计算.解答的基本方法是通过明确各种角,应用三角函数知识求解,而后比较大小.而充分利用图
形特征,则可事倍功半.
【详解】方法1:如图 为 中点, 在底面 的投影为 ,则 在底面投影 在线段 上,过
作 垂直 ,易得 ,过 作 交 于 ,过 作 ,交 于 ,则
,则 ,即 ,
,即 ,综上所述,答案为B.方法2:由最小角定理 ,记 的平面角为 (显然 )
由最大角定理 ,故选B.
方法3:(特殊位置)取 为正四面体, 为 中点,易得
,故选B.
【点睛】常规解法下易出现的错误有,不能正确作图得出各种角.未能想到利用“特殊位置法”,寻求简便
解法.
6.(2018·浙江·高考真题)已知四棱锥 的底面是正方形,侧棱长均相等, 是线段 上的点
(不含端点),设 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角
为 ,则
A. B. C. D.
【答案】D
【分析】分别作出线线角、线面角以及二面角,再构造直角三角形,根据边的大小关系确定角的大小关系.
【详解】设 为正方形 的中心, 为 中点,过 作 的平行线 ,交 于 ,过 作
垂直 于 ,连接 、 、 ,则 垂直于底面 , 垂直于 ,
因此
从而
因为 ,所以 即 ,选D.
【点睛】线线角找平行,线面角找垂直,面面角找垂面.
7.(2017·浙江·高考真题)如图,已知正四面体D–ABC(所有棱长均相等的三棱锥),P,Q,R分别
为AB,BC,CA上的点,AP=PB, ,分别记二面角D–PR–Q,D–PQ–R,D–QR–P的平面
角为α,β,γ,则A.γ<α<β B.α<γ<β C.α<β<γ D.β<γ<α
【答案】B
【详解】设O为三角形ABC中心,则正四面体D–ABC的顶点在底面ABC的投影为O,过O分别作PR、
PQ、RQ的垂线,垂足分别为E、F、G,连结DE、DF、DG,则有
所以
只需比较OE、OF、OG的大小:
在底面三角形ABC中,建立如图示的坐标系,
不妨设 ,则
所以直线RP的方程为 ,直线PQ的方程为 ,直线RQ的方程为 ,由点到
直线的距离公式,可求出: 所以 ,所以
,有α,β,γ均为锐角,所以α<γ<β.
故选:B
【点睛】立体几何是高中数学中的重要内容,也是高考重点考查的考点与热点.这类问题的设置一般有线
面位置关系的证明与角度距离的计算等两类问题.解答第一类问题时一般要借助线面平行与垂直的判定定
理进行;解答第二类问题时先建立空间直角坐标系,运用空间向量的坐标形式及数量积公式进行求解.
8.(2015·浙江·高考真题)如图,已知 , 是 的中点,沿直线 将 折成 ,所成
二面角 的平面角为 ,则A. B. C. D.
【答案】B
【详解】设 ,设 ,则由题意 ,在空间图形中,设 ,
在 中, ,
在空间图形中,过 作 ,过 作 ,垂足分别为 , ,
过 作 ,连结 ,∴ ,
则 就是二面角 的平面角,∴ ,
在 中, , ,
同理, , ,故 ,
显然 面 ,故 ,
在 中, ,
在 中,
,
∵ , ,∴ (当 时取等号),
∵ , ,而 在 上为递减函数,∴ ,故选B.
考点:立体几何中的动态问题
考点04 点面距及其应用
1.(2019·全国·高考真题)已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为 ,那么P到平面ABC的距离为 .
【答案】 .
【分析】本题考查学生空间想象能力,合理画图成为关键,准确找到 在底面上的射影,使用线面垂直定
理,得到垂直关系,勾股定理解决.
【详解】作 分别垂直于 , 平面 ,连 ,
知 , ,
平面 , 平面 ,
, . ,
,
, 为 平分线,
,又 ,
.
【点睛】画图视角选择不当,线面垂直定理使用不够灵活,难以发现垂直关系,问题即很难解决,将几何
体摆放成正常视角,是立体几何问题解决的有效手段,几何关系利于观察,解题事半功倍.