文档内容
数学参考答案·第1 页(共9 页)
数学参考答案
一、单项选择题(本大题共8 小题,每小题5 分,共40 分.在每小题给出的四个选项中,只
有一项符合题目要求)
题号
1
2
3
4
5
6
7
8
答案
B
D
C
C
B
A
D
A
【解析】
1.已知
1
i
z ,则
1
i
z ,故
(1
i)(1
i)
1
( 1)
2
zz
,故选B.
2.由题可知a
b
,故
0
a b
,即
2
0
n
,故
2
n ,故选D.
3.令2x ≥4,解得x≥2,因为
2
(
1)
x
≥1,故
1
x ≥1 或
1
x ≤1
,解得x ≥2 或x ≤0,得
到
[2
)
(
0]
[2
)
A
B
,
,
,
,
,即x
A
可以推出x
B
,而x
B
推不出x
A
,得
到“ x
A
”是“ x
B
”的充分不必要条件,故选C.
4.因为
2
n
x
x
的展开式中,二项式系数的和为64,故2
64
n
,即
6
n
,该二项式的展开
式共7 项,所以二项式系数最大的项为第4 项,故选C.
5.由sin A ∶sin B ∶sin
3
C
∶4∶5 以及正弦定理可得a ∶b ∶c =3∶4∶5,故
π
2
C
,
3
4
5
0
a
k b
k c
k
k
,
,
,
,又
2
1
12
24
2
2
ABC
k
S
ab
△
,解得
2
2
k
,
(舍),又因为
最小的边长为a ,故
3
6
a
k
,故选B.
6.
3
( )
3
2
f x
x
ax
,则
2
( )
3
3
f
x
x
a
,若
( )
f x 存在至少2 个零点,由函数单调性可知,
( )
f x 要同时存在极大值和极小值,故
0
a
,当
0
a
时,结合
( )
f
x
可知:
( )
f x 的极大值
为
(
)
f
a
,极小值为
(
)
f
a ,若
( )
f x 要存在至少2 个零点,则
(
)
0
(
)
f
a
f
a
≥,
≤0,
即
3
2
3
2
2
2
0
2
2
a
a
≥,
≤0,
解得
1
a≥,故选A.
数学参考答案·第2 页(共9 页)
7.由
0
a
,
0
b
,
2
a
b
ab
可得1
1
1
2
2
a
b
,所以1
1
2a ,即
1
2
a
,同理可得1
1
2b ,
则
1
2
b
,故A 正确;因为
0
0
a
b
,
,故2ab
a
b
≥2 ab ,当且仅当
1
a
b
时,等
号成立,所以ab ≥
ab ,即
ab ≥1,ab≥1,故B 正确;由A 可知:
1
2
a
,
1
2
b
,可
得
1
2
b
a
a
,不等式两边同时加上1
2b ,可得
1
1
1
2
2
2
b
a
b
a
b
,又1
1
1
2
2
a
b
,所以
1
1
2
b
a
b
,故C 正确;由1
1
1
2
2
a
b
可得
1
1
3
2
(
2 ) 2
2
2
2
a
b
a
b
a
b
a
b
b
a
≥3
3
2
2
2
2
2
a
b
b
a
,当且仅当2
a
b
b
a
时,即
1
2
2
2
2
4
a
b
,
时等号成立,所
以
2
a
b
≥3
2
2
,故D 错误,故选D.
8.在
(
1)
( ) ( )
( )
2
f xy
f x f y
f y
x
中,令
0
x
,得
( 1)
(0)
( )
( )
2
f
f
f y
f y
,且
(0)
1
f
,故
( 1)
2
f
;令
0
y
,得
( 1)
( )
(0)
(0)
2
f
f x
f
f
x
,所以
( )
1
f x
x
.所
以
1
1
1
1
(
1) (
2)
(
1)
1
f x
f x
x x
x
x
,所以
2025
1
1
(
1) (
2)
i
f i
f i
1
1
1
1
1
1
2025
1
1
2
2
3
2025
2026
2026
2026
…
,故选A.
二、多项选择题(本大题共3 小题,每小题6 分,共18 分.在每小题给出的四个选项中,有
多项符合题目要求,全部选对的得6 分,部分选对的得部分分,有选错的得0 分)
题号
9
10
11
答案
AC
BD
BCD
【解析】
9.对于抛物线
2
2
(
0)
y
px p
,由题中方程知
4
p
,故准线方程为
2
2
p
x
,故选项
A 正确;焦点坐标为(2,0),故选项B 错误;若
0
4
y
,则
0
2
x
,且
0
|
|
2
p
PF
x
,故
|
| 4
PF
,故选项C 正确;因为
0
0
|
|
2
2
p
PF
x
x
,点P 在抛物线C 上,故
0x ≥0,
故|
|
PF ≥2,故选项D 错误,故选AC.
10.把原样本25 个数据从小到大排列,记为:
1
2
3
25
x
x
x
x
,,,,
…
,中位数是
13
x ;去掉最大的
2 个和最小的1 个数据后,剩下22 个数据:
2
3
23
x
x
x
,,,
…
,此时数据个数为偶数,中位
数学参考答案·第3 页(共9 页)
数是
12
x 和
13
x 的平均数,而这组数互不相同,所以剩下的22 个样本数据的中位数与原样
本数据的中位数不同,故选项A 错误;25 30%
7.5
,原样本数据的30%分位数是
8x ;
22
30%
6.6
,剩下22 个数据的30% 分位数是第7 个数据,即
8x ,故选项B 正确;由
题可知:
1
2
22
3
22
3
22
3
x
x
x
,因为
1
2
x
x
,故
1
2
x
x
x
,故选项C 错误;
2
2
2
2
2
1
1
2
2
22
3
[
(
) ]
[
(
) ]
22
3
22
3
s
s
x
x
s
x
x
,而
1
2
x
x
x
,故
2
2
2
1
2
25
22
3
s
s
s
,故
选项D 正确,故选BD.
11.
1
1
1
1
1
(
)
sin(
)
sin( 2 )
sin( 3 )
sin( 4 )
sin( 50 )
sin
sin 2
2
3
4
50
2
f
x
x
x
x
x
x
x
x
…
1
1
1
sin3
sin 4
sin(50 )
( )
3
4
50
x
x
x
f x
-
…
,故
( )
f x 为R 上的奇函数,图象关于原点对
称,故选项A 错误;当
π
π
12
12
x
,
时,
π
π
π
π
2
3
6
6
4
4
x
x
,
,
,
,故
sin
y
x
,
1
1
sin 2
sin3
2
3
y
x
y
x
,
,在
π
π
12
12
,
上都是增函数,则
( )
f x 在
π
π
12
12
,
上单调递
增,选项B 正确;因为
sin
y
x
的最小正周期为2π ,
1 sin 2
2
y
x
的最小正周期为π ,
所以
( )
g x 的最小正周期为2π ,其频率
1
1
1 Hz
2π
f
T
,纯音( )
h x 的最小正周期为2π
4 ,
其频率
2
1
2 Hz
π
f
T
,声音甲的频率更低,故声音甲比纯音( )
h x 低沉,选项C 正确;
π
1
1
( )
sin
sin
sin(2
π)
sin
cos
sin 2
2
2
2
F x
x
x
x
x
x
x
,令sin
cos
x
x
t
,
[
2
2]
t
,
,平方可得:
2
1
sin 2x
t
,代入上式得
2
2
1
1
1
(
1)
2
2
2
y
t
t
t
t
,
[
2
2]
t
,
,由二次函数知识,
1
2
1
2
y
,
,故选项D 正确,故选BCD.
三、填空题(本大题共3 小题,每小题5 分,共15 分)
题号
12
13
14
答案
2.6
3
4
7
0
x
y
16 6
3
数学参考答案·第4 页(共9 页)
【解析】
12.由分布列性质,得0.2
0.3
0.3
1
a
,解得
0.2
a
,故
(
)
1 0.2
2
0.3
3 0.2
E X
4
0.3
2.6
.
13.由题意,直线AB 的斜率存在,设
1
1
2
2
(
)
(
)
A x
y
B x
y
,
,
,
,则
1
2
2
x
x
,
1
2
2
y
y
,因为
点A B
,在椭圆上,所以
2
2
2
2
1
1
2
2
1
1
8
6
8
6
x
y
x
y
,
,两式相减得,
2
2
2
2
1
2
1
2
8
6
x
x
y
y
,即
1
2
1
2
1
2
1
2
(
)(
)
(
)(
)
4
3
x
x
x
x
y
y
y
y
,整理得
1
2
1
2
1
2
1
2
3
4
y
y
x
x
x
x
y
y
,即
1
2
1
2
3
4
y
y
x
x
,所
以直线AB 的斜率为
3
4
,则直线AB 的方程为
3
1
(
1)
4
y
x
,即3
4
7
0
x
y
.
14.由题可知,球心O 为AB 的中点,对于给定的,
(
sin )
16sin
2
ABC
AB
OC
S
△
,记
点D 到平面ABC 的距离为h ,则
max
1
( )
(
)( )
3
ABC
V
S
h
△
,当面DOC 面ABC 时,h 取
最大值,故
max
2 3
h
,故
1
32 3sin
( )
(16sin )
2 3
3
3
V
,而
π
3π
4
4
,
,故
min
32 3
2
16 6
( )
3
2
3
V
.
四、解答题(本大题共5 小题,共77 分.解答应写出文字说明,证明过程或演算步骤)
15.(本小题满分13 分)
(1)证明:数列{
}
na
中,
1
1
a ,
2
6
5
a
,
当n ≥2 时,
1
1
5
6
n
n
n
a
a
a
,
即
1
1
5
5
n
n
n
n
a
a
a
a
,
即
1
1
1 (
)
5
n
n
n
n
a
a
a
a
,且
2
1
1
5
a
a
,
所以
1
{
}
n
n
a
a
是以
2
1
1
5
a
a
为首项,以1
5 为公比的等比数列.…………………(6 分)
(2)解:由(1)知
1
*
1
1
1
1
(
)
5
5
5
n
n
n
n
a
a
n
N
,
故当n ≥2 时,
1
1
1
5
n
n
n
a
a
,
1
1
2
2
1
1
(
)
(
)
(
)
n
n
n
n
n
a
a
a
a
a
a
a
a
…
,
数学参考答案·第5 页(共9 页)
故
1
2
1
1
1
1
1
5
5
5
n
n
na
…
,故
1
5
1
1
4
4
5
n
na
(n≥2),
对于
1
n ,
0
5
1
1
1
4
4
5
na
,所以
1
*
5
1
1
(
)
4
4
5
n
na
n
N
. ………………(13 分)
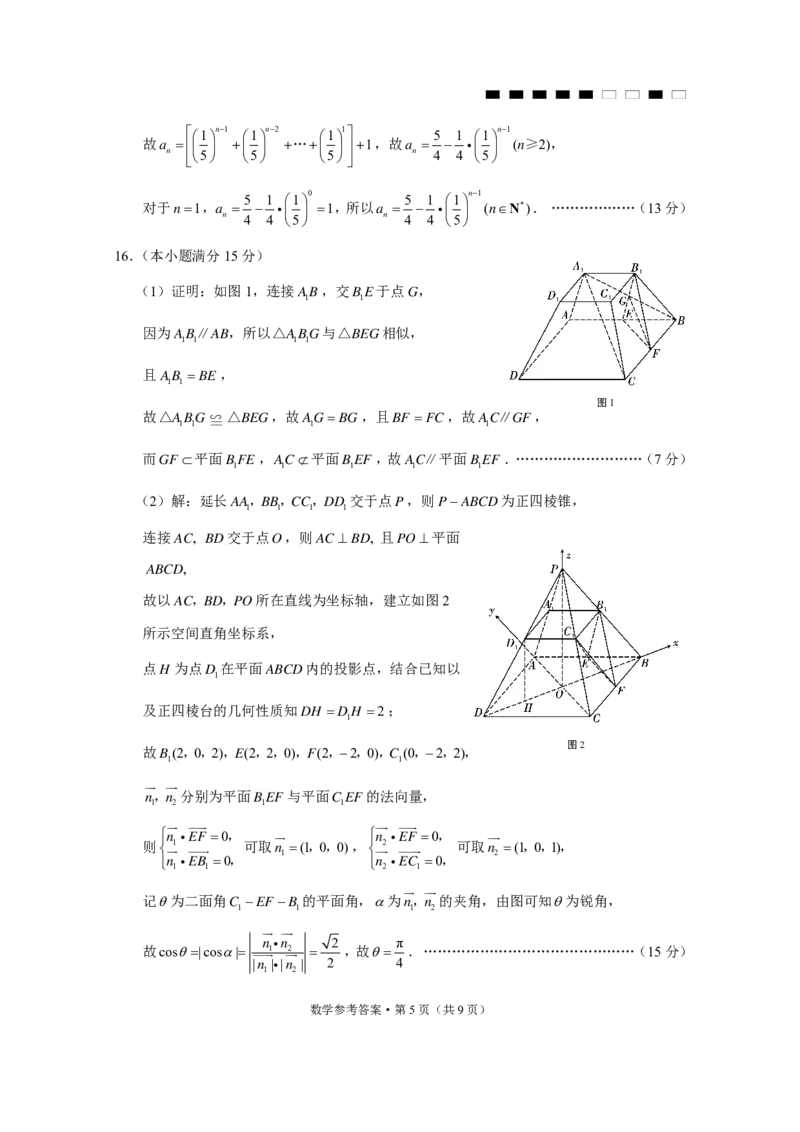
16.(本小题满分15 分)
(1)证明:如图1,连接
1A B ,交
1B E 于点G,
因为
1
1
A B∥AB,所以
1
1
A B G
△
与
BEG
△
相似,
且
1
1
A B
BE
,
故
1
1
A B G
△
∽
==
BEG
△
,故
1AG
BG
,且BF
FC
,故
1AC
GF
∥
,
而GF 平面
1B FE ,
1AC 平面
1B EF ,故
1AC∥平面
1B EF .………………………(7 分)
(2)解:延长
1
1
1
1
AA
BB
CC
DD
,
,
,
交于点P ,则P
ABCD
为正四棱锥,
连接AC
BD
,
交于点O ,则AC
BD
,且PO 平面
ABCD,
故以AC
BD PO
,
,
所在直线为坐标轴,建立如图2
所示空间直角坐标系,
点H 为点
1
D 在平面ABCD 内的投影点,结合已知以
及正四棱台的几何性质知
1
2
DH
D H
;
故
1
1
(2 0 2)
(2 2 0)
(2
2 0)
(0
2 2)
B
E
F
C
,,,
,,,
,
,,
,
,,
1
2
n
n
,
分别为平面
1B EF 与平面
1
C EF 的法向量,
则
1
1
1
0
0
n
EF
n
EB
,
,
可取
1
(1 0 0)
n
,,
,
2
2
1
0
0
n
EF
n
EC
,
,
可取
2
(1 0 1)
n
,,,
记为二面角
1
1
C
EF
B
的平面角,为
1
2
n
n
,
的夹角,由图可知为锐角,
故
1
2
1
2
2
cos
| cos
|
2
|
| |
|
n
n
n
n
,故
π
4
. ………………………………………(15 分)
图1
图2
数学参考答案·第6 页(共9 页)
17.(本小题满分15 分)
(1)证明:若
0
a ,则
2
3
( )
2
f x
x
x
,欲证
( )
f x ≥1
2
ln x
在[1,+∞)上恒成立,
即证明:
2
3
1
ln
2
2
x
x
x
≥0 在[1,+∞)上恒成立,
令
2
3
1
( )
ln
2
2
g x
x
x
x
,
则
2
1
13
3
6
1
3
2
1
( )
1
x
x
g x
x
x
,
令
2
1
13
( )
3
6
12
h x
x
,又x≥1,
故( )
h x ≥1,则
( )
0
g x
,
故( )
g x 在[1,+∞)上单调递增,则( )
g x ≥( )1
g
,即( )
g x ≥0,
故
( )
f x ≥1
ln
2
x
在[1,+∞)上恒成立.
…………………………………………………………………………………(7 分)
(2)解:
2
3
(3
1)
(3
1)(
)
( )
3
(3
1)
a
x
a
x
a
x
x
a
f
x
x
a
x
x
x
,
①若a ≤0,则当
1
0 3
x
,
时,
( )
0
f
x
,
( )
f x 单调递减,
当
1
3
x
,
时,
( )
0
f
x
,
( )
f x 单调递增;
②若
1
0
3
a
,则当
(0
)
x
a
,
时,
( )
0
f
x
,
( )
f x 单调递增,
当
1
3
x
a
,
时,
( )
0
f
x
,
( )
f x 单调递减,
当
1
3
x
,
时,
( )
0
f
x
,
( )
f x 单调递增;
③若
1
3
a
,则当
(0
)
x
,
时,
( )
f
x
≥0,
( )
f x 单调递增;
④若
1
3
a
,则当
1
0 3
x
,
时,
( )
0
f
x
,
( )
f x 单调递增,
当
1
3
x
a
,
时,
( )
0
f
x
,
( )
f x 单调递减,
当
(
)
x
a
,
时,
( )
0
f
x
,
( )
f x 单调递增.
综上,当a≤0,
( )
f x 的单调递减区间为
1
0 3
,
,单调递增区间为1
3
,
;
数学参考答案·第7 页(共9 页)
当
1
0
( )
3
a
f x
,
的单调递减区间为
1
3
a
,
,单调递增区间为(
1
0
3
)
a
,,
,
;
当
1
3
a
,
( )
f x 无单调递减区间,单调递增区间为(0,+∞);
当
1
3
a
,
( )
f x 的单调递减区间为1
3
a
,
,单调递增区间为
1
0
(
)
3
a
,
,,
.
…………………………………………………………………………………(15 分)
18.(本小题满分17 分)
(1)解:甲赢得挑战的概率为:1
1
1
1
1
1
1
1
1
5
1
3
3
3
3
3
3
3
3
3
243
.
……………………………………………………………………………………(4 分)
(2)(i)解:
4
4
2
65
1
3
81
P
;当乙同学回答完6 道题目后,出现连续答对至少4 道题
这一情形,可能的情况为:6 道都答对、连续答对5 道(第1 道或者第6 道答错)、连续
答对4 道(1~4 道答对,第5 道答错,第六道答对或者答错;第1 道答错,2~5 道答对,
第6 道答错;第1 道答对或答错,第2 道答错,3~6 道答对),
故
6
5
1
4
1
4
2
4
1
6
2
2
1
2
1
2
1
2
1
163
1
2
3
3
3
3
3
3
3
3
3
243
P
;
……………………………………………………………………………………(10 分)
(ii)证明:乙同学答完n 道题后,如果没有出现连续答对至少4 道题的情形,
则由题意可如下分类:
① 第n 题答错,且前
1
n 题未出现连续答对至少4 道题的情形,此时概率为
1
1
3
nP ;
② 第n 题答对,第
1
n 题答错,且前
2
n
题未出现连续答对至少4 道题的情形,此时概
率为
2
2
1
3
3
nP
;
③ 第n 题答对,第
1
n 题答对,第
2
n
题答错,且前
3
n
题未出现连续答对至少4 道题
的情形,此时概率为
3
2
2
1
3
3
3
nP
;
④第n 题答对,第
1
n 题答对,第
2
n
题答对,第
3
n
题答错,且前
4
n
题未出现连续
答对至少4 道题的情形,此时概率为
4
2
2
2
1
3
3
3
3
nP
,
由全概率公式:
1
2
3
4
1
2
1
2
2
1
2
2
2
1
(
3
3
3
3
3
3
3
3
3
3
n
n
n
n
n
P
P
P
P
P
n
≥
*
6
)
nN
,
①,
数学参考答案·第8 页(共9 页)
因此
1
2
3
4
5
1
2
1
2
2
1
2
2
2
1
3
3
3
3
3
3
3
3
3
3
n
n
n
n
n
P
P
P
P
P
(n ≥
*
6
)
nN
,
②,
2
3
①-
②:
1
5
16
243
n
n
n
P
P
P
≤0(n ≥
*
6
)
nN
,
,
所以当n ≥6,
*
nN 时,
nP ≤
1
nP ,故
100
P
≤
99
P .…………………………………(17 分)
19.(本小题满分17 分)
(1)解:由题可知,
10
0
0
2
c
a
b
a
,
,
,
2
a
,且
2
2
2
c
a
b
,故
3
b
,
故此时C 的方程为
2
2
1
2
3
x
y
.…………………………………………………………(4 分)
(2)(i)证明:设
0
0
(
)
M x
y
,
,由题可知M 点处的切线方程为
0
0
2
2
1
x x
y y
a
b
,
故直线m 的斜率为
2
0
2
0
m
b x
k
a y
,且
1
0
0
MF
y
k
x
c
,
2
0
0
MF
y
k
x
c
,
记直线m 与直线
1
MF 的夹角为,记直线m 与直线
2
MF 的夹角为,直线m 与x 轴交于
点E,而
2
1
1
2
MEF
MF E
MEF
MF E
,
,
故
1
1
2
2
2
0
2
1
2
2
0
0
0
(
)
tan
tan(
)
1
(
)
m
MF
m
MF
k
k
b
a
cx
b
MEF
MF E
k k
y a c
c x
cy
,
2
2
2
2
2
0
1
2
2
2
0
0
0
(
)
tan
tan(
)
1
(
)
m
MF
m
MF
k
k
b cx
a
b
MEF
MF E
k k
y c x
a c
cy
,则tan
tan
,
且
π
0
2
,
,
,故
,即切线m 平分
1
2
F MF
;……………………………(10 分)
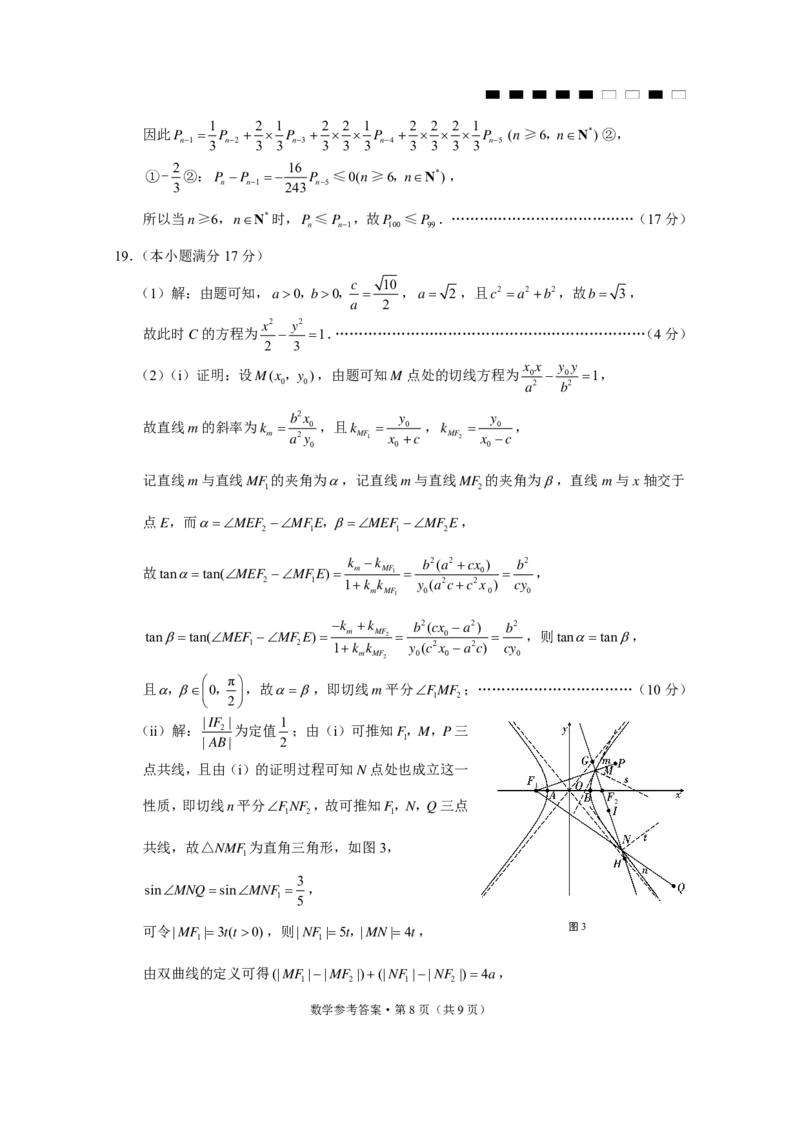
(ii)解:
2
|
|
|
|
IF
AB 为定值1
2 ;由(i)可推知
1F
M
P
,,三
点共线,且由(i)的证明过程可知N 点处也成立这一
性质,即切线n 平分
1
2
F NF
,故可推知
1F
N Q
,,三点
共线,故
1
NMF
△
为直角三角形,如图3,
1
3
sin
sin
5
MNQ
MNF
,
可令
1
|
| 3 (
0)
MF
t t
,则
1
|
| 5
|
| 4
NF
t
MN
t
,
,
由双曲线的定义可得
1
2
1
2
(|
|
|
|)
(|
|
|
|)
4
MF
MF
NF
NF
a
,
图3
数学参考答案·第9 页(共9 页)
即
1
1
|
|
|
|
|
| 4
MF
NF
MN
a
,即3
5
4
4
t
t
t
a
,所以t
a
,
所以
1
1
|
| 3
|
| 5
|
|
4
MF
a
NF
a
MN
a
,
,
,
所以
2
1
|
| |
| 2
MF
MF
a
a
,
在直角
2
1
F MF
△
中,
1
2
1
2
|
|
tan
3
|
|
MF
MF F
MF
,
所以直线
2
MF (即直线l)的方程为
3(
)
y
x
c
,
由
2
2
2
1
2
1
2
|
|
|
|
|
|
MF
MF
F F
,得
2
2
2
9
4
a
a
c
,
所以
2
2
2
2
5
2
c
a
a
b
,所以
2
2
3
2
a
b
,
所以两条渐近线的方程为
2
2
3
2
y
x
,且双曲线C 的离心率
10
2
e
,
由题可知直线
3(
)
y
x
c
,与双曲线C 的两条渐近线都相交,
联立
2
2
3(
)
3
2
y
x
c
y
x
,得
2
2
5
12
6
0
x
cx
c
,
设
1
1
2
2
(
)
(
)
G x
y
H x
y
,
,
,
,则
2
1
2
1
2
12
6
5
5
c
c
x
x
x x
,
,
故
1
2
1
2
6
3(
)
6
5
c
y
y
x
x
c
,所以
6
3
5
5
c
c
I
,
,
所以
2
2
2
6
3
10
|
|
0
5
5
5
c
c
IF
c
c
,
所以
2
10
|
|
10
1
5
|
|
2
10
2
c
IF
e
AB
a
,所以
2
|
|
|
|
IF
AB 为定值1
2 .……………………………(17 分)