文档内容
2024届新高三开学摸底考试卷(北京专用)
数学·答案及评分标准
1 2 3 4 5 6 7 8 9 10
A C D D C C D B D A
11. (5分)
12. (5分)
13.5 (5分)
14. (5分)
15.①③④
16.(1)若选①:
因为 ,由余弦定理得 ,整理得 ,则 ,(3分)
又 ,则 , ,(5分)
则 ;(6分)
若选②:
因为 ,即 ,则 ,(2分)
又 ,则 ,
又 ,得 ,(4分)
则 ;(6分)
(2)由正弦定理得: ,则 ,(10分)
则 , .(13分)
17.(1)这10名学生的考核成绩(单位:分)分别为:
93,89.5,89.5,88,90,89,91.5,91,90.5,91.
其中大于90分的有1号、7号、8号、9号、10号,共5人, (2分)所以样本中学生考核成绩大于90分的频率是 .
从该校高二年级随机选取一名学生,估计这名学生考核成绩大于90分的概率为0.5;(4分)
(2)由题知,考核成绩小于90分的学生共4人,其中两轮测试至少有一次大于90分学生有2人.
所以 可取0,1,2,则
, , ,(7分)
所以 的分布列为
0 1 2
所以 ;(9分)
(3)由题可得 ,
,
(12分)
,
所以 ; .(13分)
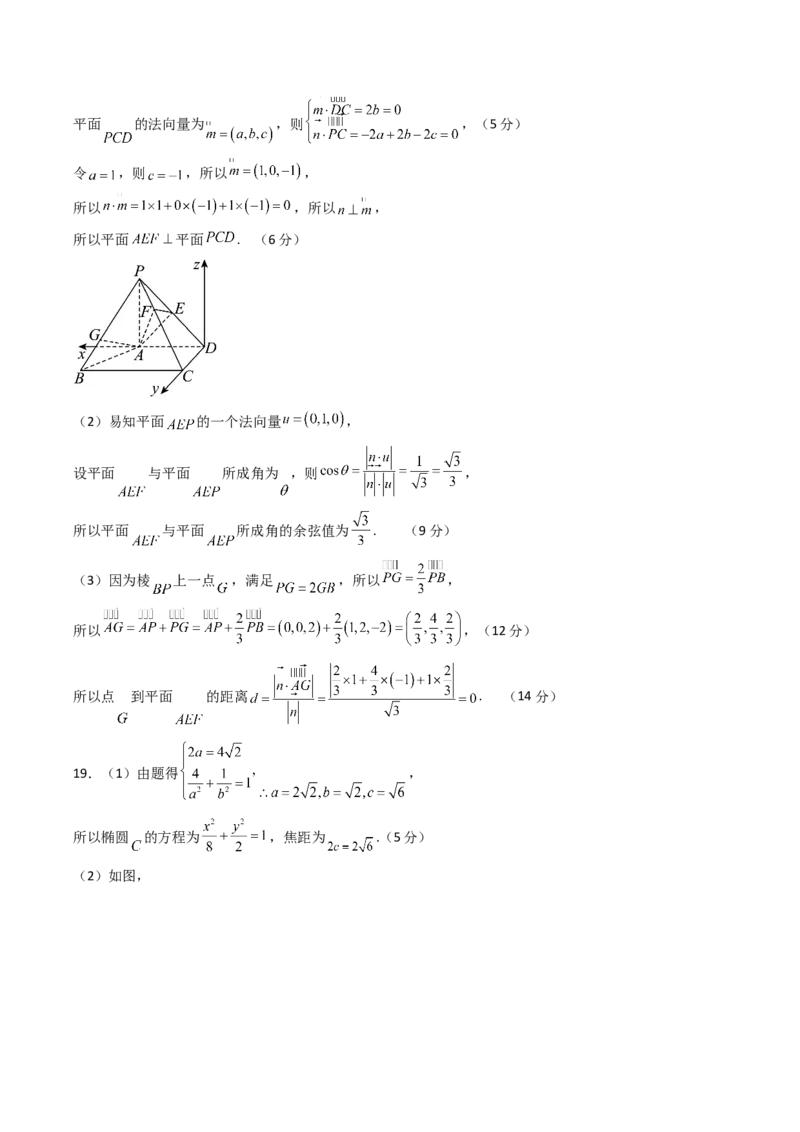
18.(1)如图,以 为原点,分别以 , 为 轴, 轴,过 作 平行线为 轴,建立空间直角坐
标系,
则 , , , , , ,(1分)
所以 , ,因为 ,所以 ,
所以 ,即 ,
所以 , ,
设平面 的法向量为 ,则 ,(3分)
令 ,则 ,所以 ,平面 的法向量为 ,则 ,(5分)
令 ,则 ,所以 ,
所以 ,所以 ,
所以平面 平面 . (6分)
(2)易知平面 的一个法向量 ,
设平面 与平面 所成角为 ,则 ,
所以平面 与平面 所成角的余弦值为 . (9分)
(3)因为棱 上一点 ,满足 ,所以 ,
所以 ,(12分)
所以点 到平面 的距离 . (14分)
19.(1)由题得 ,
所以椭圆 的方程为 ,焦距为 .(5分)
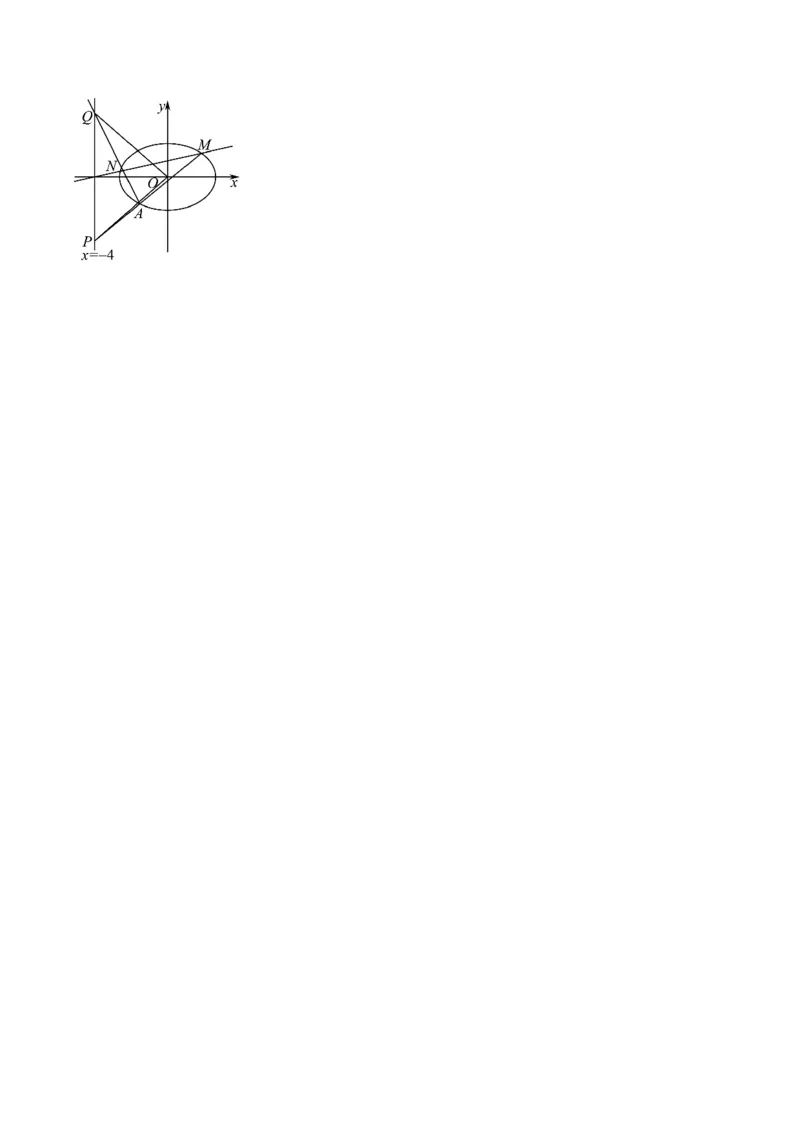
(2)如图,直线 与椭圆方程 联立,
化简得 , (7分)
,即 .
设 , , , ,则 , .
直线 的方程为 ,则 ,(9分)
直线 的方程为 ,则 ,
因为 ,所以 + =0,(11分)
所以 ,
所以 ,
把韦达定理代入整理得 或 ,
当 时,直线方程为 ,过定点 ,(13分)
即点 ,不符合题意,所以舍去.
当 时,直线方程为 ,
过定点 .
所以直线 经过定点. (15分)
20.(1)当 时, , ,
所以 , (3分)
又 ,
所以切线方程为 ,即 . (5分)
(2) ,
当 时, ,解得 ,
故 时, , 单调递减; 时, , 单调递增, (6分)
故 时, 的极小值为 ,无极大值;
当 时,令 ,解得 , ,
故当 或 时, , 单调递增, (7分)当 时, , 单调递减,故 的极大值为 ,极小值为 ;
当 时,令 ,解得 , ,
故当 或 时, , 单调递减,
当 时, , 单调递增,
故 的极大值为 ,极小值为 ; (10分)
综上,当 时, 的极小值为 ,无极大值;当 时, 的极大值为 ,极
小值为 . (11分)
(3)当 时,由(2)知, 在 和 上单调递增,
在 上单调递减,且 时, 恒成立, (12分)
时, ,
又 的极大值为 ,极小值为 ,
所以存在实数 时,函数 有三个零点. (15分)
21.(1)当 时, , ,
,所以 , (2分)
(2)设 ,其中 ,
则 ,
(4分)
因 ,
,
因 ,
所以 , , , ,
又 ,, ,所以 , (6分)
因 , , ,
,
因 , , , ,
所以 , , , ,
, , ,
所以
所以 为定值. (8分)
(3) ,
若 ,
则 ,
,
故 ,
,
此时 ,不符合题意, (10分)
故 ,
猜想 ,下面给予证明,
当 时,显然成立,
假设当 , 时,都有 成立,即 ,
此时 , ,
故 , ,
,符合题意, (12分)
,
则 ,
,
若 ,
的元素个数小于的元素个数则有 ,
不符合题意,故 , (14分)
综上,对于任意的 ,都有
故数列 的通项公式 . (15分)公众号:高中试卷君