文档内容
2024届新高三开学摸底考试卷(北京专用)
数 学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡
皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)
一、选择题共10小题,每小题4分,共40分,在每小题列出的四个选项中,选出符合题目
要求的一项.
1.若 ,则复数z的虚部为( )
A.-5 B.5 C.7 D.-7
2.已知集合 , ,则 ( )
A. B.
C. D. 或
3.设 ,则 ( )
A. B. C.1 D.2
4.设 , 为两个不同的平面,则 ∥ 的一个充分条件是( )
A. 内有无数条直线与 平行 B. , 垂直于同一个平面
C. , 平行于同一条直线 D. , 垂直于同一条直线
5.已知双曲线 的左右焦点分别为 ,过 的直线分别交双曲线 的左右两支于 两点,
且 ,则 ( )
A. B. C. D.
6.记 为数列 的前 项和,设甲: 为等差数列;乙: 为等差数列,则( )
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件7.已知函数 则下列结论正确的是( ).
A. , B. ,
C.函数 在 上单调递增 D.函数 的值域是
8.在平面直角坐标系中, 为坐标原点,已知圆 的半径为3,直线 , 互相垂直,垂足为 ,
且 与圆 相交于 , 两点, 与圆 相交于 , 两点,则四边形 的面积的最大值为( )
A.10 B.12 C.13 D.15
9.已知函数 在区间 单调递增,直线 和 为函数 的图像的两条
对称轴,则 ( )
A. B. C. D.
10.随着科技的不断发展,人民消费水平的提升,手机购物逐渐成为消费的主流,当我们打开购物平台时,
会发现其首页上经常出现我们喜欢的商品,这是电商平台推送的结果.假设电商平台第一次给某人推送某
商品,此人购买此商品的概率为 ,从第二次推送起,若前一次不购买此商品,则此次购买的概率为 ;
若前一次购买了此商品,则此次仍购买的概率为 .记第n次推送时不购买此商品的概率为 ,当 时,
恒成立,则M的最小值为( )
A. B. C. D.
第二部分(非选择题 共110分)
二、填空题共5小题,每小题5分,共25分.
11.已知点 在抛物线C: 上,则A到C的准线的距离为______.
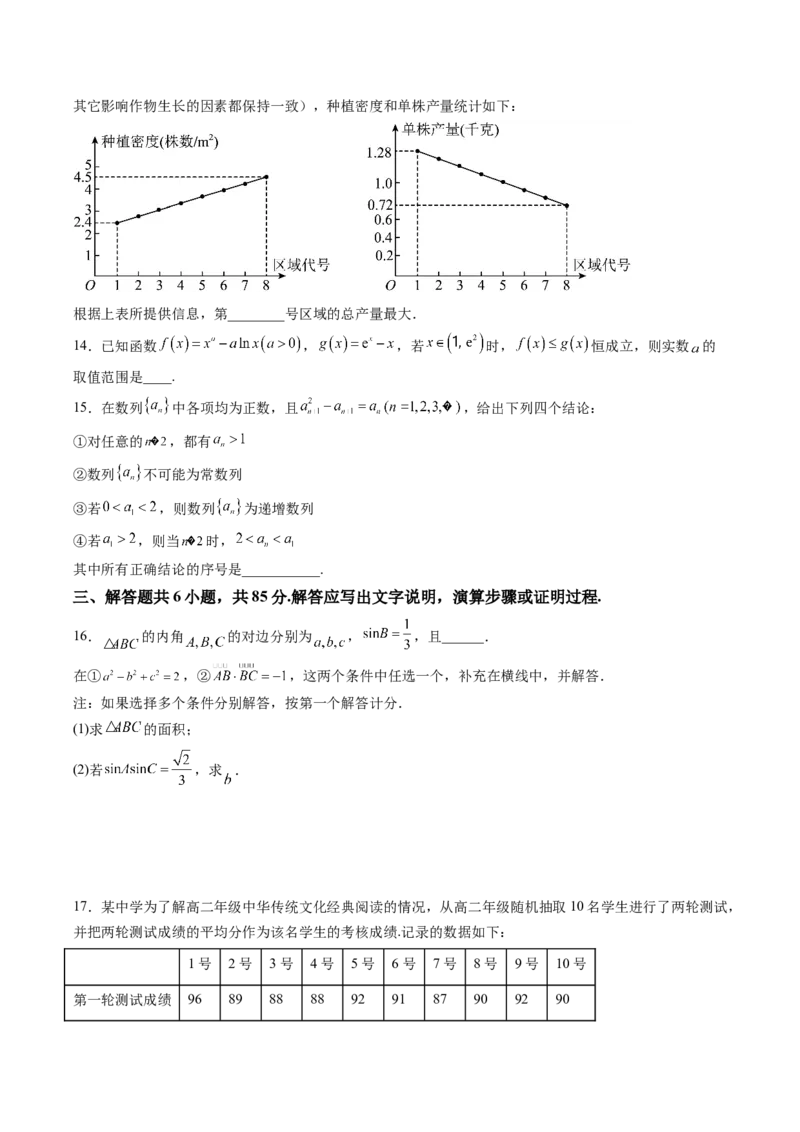
12.如图, 是半径为3的圆 的两条直径, ,则 __________.13.农业技术员进行某种作物的种植密度试验,把一块试验田划分为8块面积相等的区域(除了种植密度,其它影响作物生长的因素都保持一致),种植密度和单株产量统计如下:
根据上表所提供信息,第________号区域的总产量最大.
14.已知函数 , ,若 时, 恒成立,则实数 的
取值范围是____.
15.在数列 中各项均为正数,且 ,给出下列四个结论:
①对任意的 ,都有
②数列 不可能为常数列
③若 ,则数列 为递增数列
④若 ,则当 时,
其中所有正确结论的序号是___________.
三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.
16. 的内角 的对边分别为 , ,且______.
在① ,② ,这两个条件中任选一个,补充在横线中,并解答.
注:如果选择多个条件分别解答,按第一个解答计分.
(1)求 的面积;
(2)若 ,求 .
17.某中学为了解高二年级中华传统文化经典阅读的情况,从高二年级随机抽取10名学生进行了两轮测试,
并把两轮测试成绩的平均分作为该名学生的考核成绩.记录的数据如下:
1号 2号 3号 4号 5号 6号 7号 8号 9号 10号
第一轮测试成绩 96 89 88 88 92 91 87 90 92 90第二轮测试成绩 90 90 91 88 88 87 96 92 89 92
(1)从该校高二年级随机选取一名学生,试估计这名学生考核成绩大于90分的概率;
(2)为进一步研究这10名同学的成绩,从考核成绩小于90分的学生中随机抽取两人,记这两人中两轮测试
至少有一次大于90分的人数为 ,求 的分布列与数学期望;
(3)记抽取的10名学生第一轮测试的平均数和方差分别为 ,考核成绩的平均数和方差分别为 ,试
比较 与 与 的大小.(只需写出结论)
18.如图,在四棱锥 中, 平面 , , , , .
为 的中点,点 在 上,且 .
(1)求证:平面 平面 ;
(2)求平面 与平面 所成角的余弦值;
(3)若棱 上一点 ,满足 ,求点 到平面 的距离.
19.已知椭圆 过点 ,长轴长为 .
(1)求椭圆 的方程及其焦距;
(2)直线 与椭圆 交于不同的两点 ,直线 分别与直线 交于点 , 为坐
标原点且 ,求证:直线 过定点,并求出定点坐标.
20.已知函数 .(1)若 ,求 在 处切线方程;
(2)求 的极大值与极小值;
(3)证明:存在实数 ,当 时,函数 有三个零点.
21.已知 为有限个实数构成的非空集合,设 , ,记集
合 和 其元素个数分别为 , .
设 .例如当 时, , , ,所以
.
(1)若 ,求 的值;
(2)设 是由3个正实数组成的集合且 ,证明: 为定值;
(3)若 是一个各项互不相同的无穷递增正整数数列,对任意 ,设 , .
已知 ,且对任意 ,求数列 的通项公式.公众号:高中试卷君