文档内容
2024届新高三开学摸底考试卷(全国卷)
文科数学 02
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标
号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一个选项是符合题目要求的.
1.若集合 , ,则 ( )
A. B. C. D.
【答案】D
【分析】分别解出集合 ,即可求得 .
【详解】解: , ,
, ,
.
故选:D.
【点睛】本题主要考查的是集合的并集运算,正确解出集合是解决本题的关键,是基
础题.
2.若 ,则
A. B. C. D.
【答案】C【分析】先利用复数乘法的运算化简复数 ,再利用复数模的公式求解即可.
【详解】因为 ,所以 .故选C.
【点睛】本题考查了复数的运算法则、模的计算公式,属于基础题.复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部
的理解,掌握纯虚数、共轭复数、复数的模这些重要概念,复数的运算主要考查除法
运算,通过分母实数化转化为复数的乘法,运算时特别要注意多项式相乘后的化简,
防止简单问题出错,造成不必要的失分.
3.设函数 ,且 为奇函数,则 ( )
A. B. C. D.
【答案】D
【分析】利用分段函数、奇函数的性质求解.
【详解】因为 ,所以 ,
又 为奇函数,所以 ,
所以 ,故A,B,C错误.
故选:D.
4.甲,乙,丙,丁四人在足球训练中进行传球训练,从甲开始传球,甲等可能地把球
传给乙,丙,丁中的任何一个人,以此类推,则经过3次传球后乙恰接到1次球的概
率为( )
A. B. C. D.
【答案】C
【分析】将所有传球的结果列出,再利用古典概型求结果.
【详解】传球的结果可以分为:
分别传给3人时:乙丙丁,乙丁丙,丙乙丁,丙丁乙,丁乙丙,丁丙乙,共6种;
若传给2人时:乙丙乙,丙乙丙,乙丁乙,丁乙丁,丁丙丁,丙丁丙,共6种;
再传给甲的:乙甲乙,丙甲丙,丁甲丁,乙丙甲,乙甲丙,乙丁甲,乙甲丁,丙乙甲,
丙甲乙,丁乙甲,丁甲乙,丙丁甲,丙甲丁,丁甲丙,丁丙甲,共15种;
共27种,只传乙一次的有16种,所以所求概率为故选:C5.“埃拉托塞尼筛法”是保证能够挑选全部素数的一种古老的方法.这种方法是依次
写出2和2以上的自然数,留下第一个数2不动,剔除掉所有2的倍数;接着,在剩余
的数中2后面的一个数3不动,剔除掉所有3的倍数;接下来,再在剩余的数中对3后
面的一个数5作同样处理;……,依次进行同样的剔除.剔除到最后,剩下的便全是素
数.在利用“埃拉托塞尼筛法”挑选2到20的全部素数过程中剔除的所有数的和为(
)
A.130 B.132 C.134 D.141
【答案】B
【分析】利用等差数列求和公式及素数的定义即可求解.
【详解】由题可知,2到20的全部整数和为 ,
2到20的全部素数和为 ,
所以挑选2到20的全部素数过程中剔除的所有数的和为 .
故选:B.
6.已知函数 的最小正周期为T,且 ,若
的图象关于直线 对称,则 ( )
A. B. C. D.
【答案】A
【分析】运用二倍角公式化简 ,结合 与 的对称性求得 的值,进
而求得结果.
【详解】因为 ,
所以 .
又因为 ,所以 ,即 ,①
又因为 的图象关于直线 对称,
所以 , .
所以 , ,②
所以由①②得 ,
所以 ,故 .
故选:A.
7.在 ABC中,角A,B,C所对的边分别为a,b,c,若 ,则角C
△
=( )
A. B. C. D.
【答案】A
【分析】利用余弦定理求出 的值,结合角 的取值范围可求得角 的值.
【详解】由余弦定理可得 ,
, .
故选: .
8.在 中,点 在边 上,且 ,则( )
A. B.
C. D.
【答案】D
【分析】利用向量的线性运算法则计算即可.
【详解】因为点 在边 上,且 ,所以 ,
所以 ,
故选:D
9.贯耳瓶流行于宋代,清代亦有仿制,如图所示的青花折枝花卉纹六方贯耳瓶是清乾
隆时期的文物,现收藏于首都博物馆,若忽略瓶嘴与贯耳,把该瓶瓶体看作3个几何
体的组合体,上面的几何体Ⅰ是直棱柱,中间的几何体Ⅱ是棱台,下面的几何体Ⅲ也
是棱台,几何体Ⅲ的下底面与几何体Ⅰ的底面是全等的六边形,几何体Ⅲ的上底面面
积是下底面面积的4倍,若几何体Ⅰ、Ⅱ、Ⅲ的高之比分别为 ,则几何体Ⅰ、
Ⅱ、Ⅲ的体积之比为( )A. B. C. D.
【答案】D【分析】设上面的六棱柱的底面面积为S,高为 ,根据棱柱和棱台的体积公式直接
计算,然后求比可得.
【详解】设上面的六棱柱的底面面积为S,高为 ,由上到下的三个几何体体积分别
记为 ,
则 ,
,
,
所以
故选:D
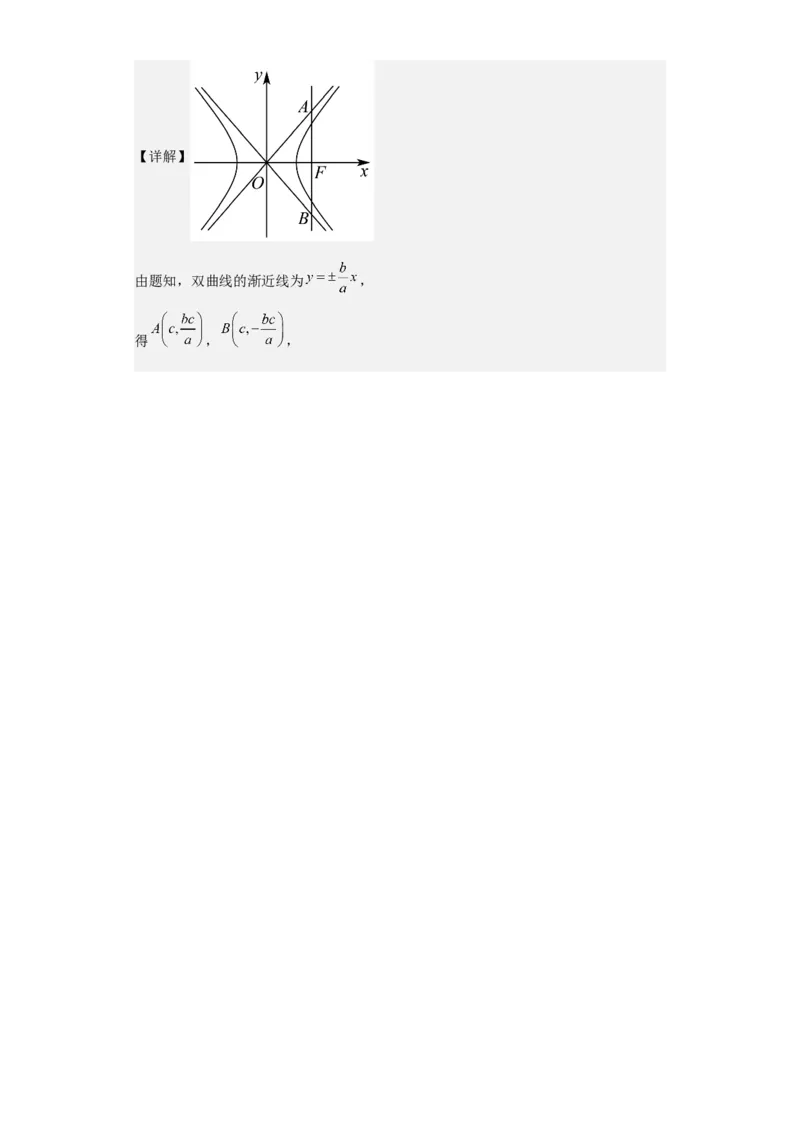
10.已知过双曲线 : 的右焦点 作 轴的垂线与两条渐
近线交于 , , 的面积为 ,则该双曲线的离心率为( )
A. B. C.2 D.
【答案】A
【分析】先结合双曲线的渐近线方程求出 ,再根据三角形面积公式得到
即可.【详解】
由题知,双曲线的渐近线为 ,
得 , ,,
,
,
故选:A.
11.已知直线 上的两点 ,且 ,点 为圆
上任一点,则 的面积的最大值为( )
A. B. C. D.
【答案】A
【分析】找到圆上的点到直线距离的最大值作为 的高,再由面积公式求解即可.
【详解】把圆 变形为 ,
则圆心 ,半径 ,
圆心 到直线 的距离 ,
则圆 上的点到直线 的距离的最大值为 ,又 ,
∴ 的面积的最大值为 .
故选:A.
12. , , ,则 的大小关系为( ).
A. B.
C. D.
【答案】B
【分析】分别构造函数证明 与 ,利用这两个不等式可判
断 ;构造函数 ,可证得 ,即可判断 ,从而得出答案.
【详解】令 ,则 ,
则 在 上单调递增,故 ,则 .令 ,则 ,
则 在 上单调递增,故 ,则 .
所以 ,即 ;
令 ,则 ,
因为 ,所以 ,则 ,故 ,
所以 在 上单调递增,则 ,即 ,
易知 ,所以 ,则 ,即 ;
综上: .
故选:B.
第Ⅱ卷
二、填空题:本题共4小题,每小题5分,共20分.
13.若某种水果的果实横径 (单位: )服从正态分布 ,则果实横径在
的概率为__________.(附:若 ,则 ,
)
【答案】
【分析】分析可得 , ,利用 原则结合参考数据可求得结果.
【详解】由题意可得 , ,则 , ,
所以,
.
故答案为: .
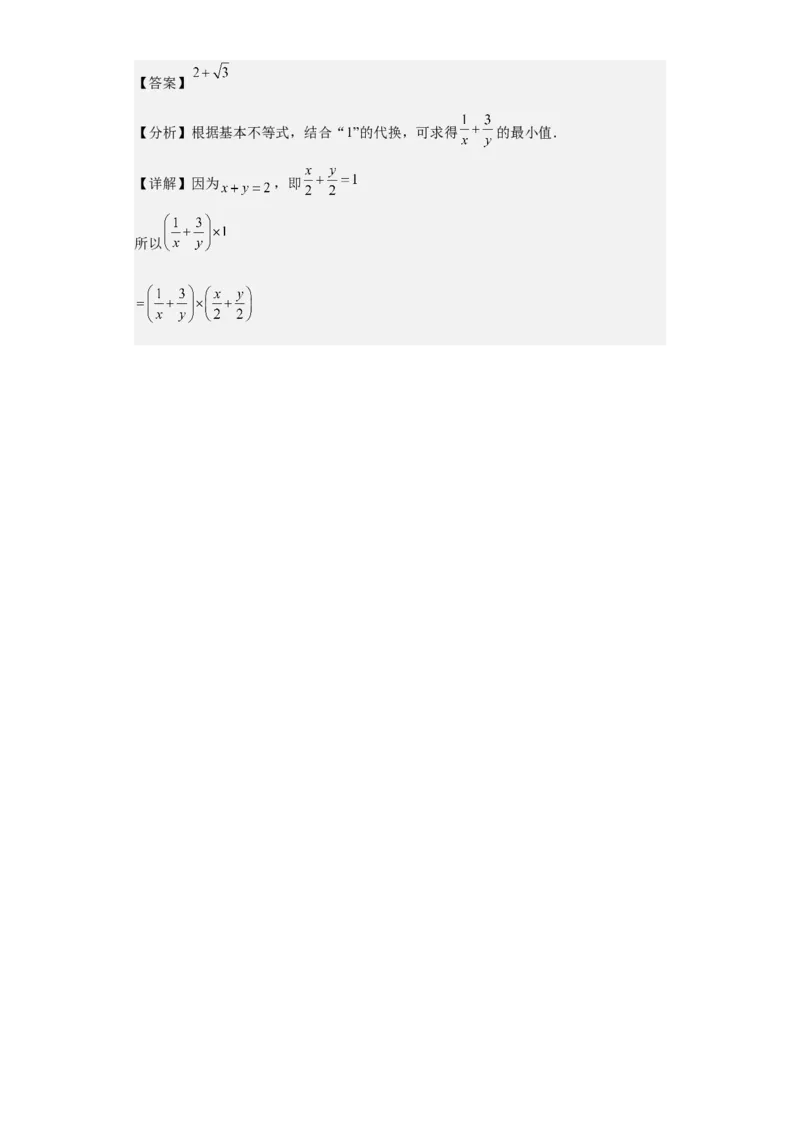
14.已知 , 且 ,则 的最小值为________.【答案】
【分析】根据基本不等式,结合“1”的代换,可求得 的最小值.
【详解】因为 ,即
所以,当且仅当 时取得等号
所以 的最小值为
【点睛】本题考查了基本不等式的简单应用,属于基础题.
15.已知圆 : 与圆 : 的交点为A,B,则
________.
【答案】
【分析】两圆方程作差得到公共弦方程,利用圆 的圆心到直线的距离及勾股定理求
出弦长.
【详解】解:两圆的公共弦 的方程为 ,即
,圆 : 配成标准式得 知圆心为
,半径 ,则点 到直线 的距离 ,则 .
故答案为
【点睛】本题考查两圆的公共弦方程,圆中的弦长问题,属于基础题.
16.如图,已知三棱锥 中, , , ,则
二面角 的平面角的大小为______.
【答案】60°
【分析】取 中点 ,由等腰三角形三线合一可知 , ;由二面角平面角定义可知 为所求角,根据长度关系可知 为等边三角形,从而得到
结果.
【详解】取 中点 ,连接, , 为 中点 ,
即为二面角 的平面角
又 , 为等边三角形
,即二面角 的大小为
故答案为
【点睛】本题考查立体几何中二面角的求解问题,关键是能够根据二面角平面角的定
义,利用垂直关系在图形中得到二面角的平面角.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必
考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
17.已知数列 和 满足 .
(1)证明: 和 都是等比数列;
(2)求 的前 项和 .
【答案】(1)证明见解析
(2)
【分析】(1)由 , 两式相加、相减,结合等比数列的定义即
可证明;
(2)由(1)可得 , ,即可求出 和 的通项公式,
从而得到 ,再利用分组求和法及等边数列求和公式计算可得.【详解】(1)因为 , ,
所以 , ,
又由 , 得 , ,所以数列 是首项为 ,公比为 的等比数列,
数列 是首项为 ,公比为 的等比数列.
(2)由(1)得 , ,
所以 , ,
所以 ,
所以 .
18.如图,平面 平面 , , , , .
(1)求证: 平面 ;
(2)求证: .
【答案】(1)证明见解析;(2)证明见解析.
【分析】(1)过点 分别作 、 的平行线,交点为 、 ,利用平行关系和线段
长度关系证明四边形 为平行四边形,从而有 ,再利用线面平行的判
定定理证明 平面 ;(2)利用面面垂直的性质得到 平面 ,从而
,又由 ,得 .
【详解】(1) 证明:过点 作 的平行线,交 于点 ,连接 .
过点 作 的平行线交 于点 ,连接 .
则四边形 为平行四边形,有 平行且等于 .
因为 ,所以 .
因为 ,所以 ,故 ,所以 ,
又 ,所以四边形 为平行四边形,有 平行且等于 ,所以 平行且等于 ,四边形 为平行四边形,有 .
又 平面 , 平面 ,所以 平面 .
(2)证明:因为 , ,所以 .
因为平面 与平面 垂直,且交线为 ,又 平面 ,
所以 平面 ,又 平面 ,所以 .
又由(1)知 ,所以 .
19.某购物中心准备进行扩大规模,在制定末来发展策略时,对中心的现有顾客满意
度进行了一个初步的现场调查,分别调查顾客对购物中心的商品质量、服务质量、购
物环境、广告宣传的满意程度.调查时将对被抽中的每个顾客从这四个问题中随机抽
取两个问题来提问,统计顾客的满意情况.假设,有三名顾客被抽到,且这三名顾客
对这四个问题的满意情况如下表:
商品质量 服务质量 购物环境 广告宣传
顾客
满意 不满意 满意 不满意
甲
顾客
不满意 满意 满意 满意
乙
顾客
满意 满意 满意 不满意
丙
每得到一个满意加10分,最终以总得分作为制定发展策略的参考依据.
(1)求购物中心得分为50分的概率;
(2)若已知购物中心得分为50分,则顾客丙投出一个不满意的概率为多少?
(3)列出该购物中心得到满意的个数X的分布列,并求得分 的数学期望.
【答案】(1)
(2)(3)分布列见解析,40【分析】(1)得分为50分即在六个问题的结果中,有五个满意,一个不满意,然后
按照古典概型的概率进行计算;
(2)由条件概率的公式进行计算即可;
(3)按求分布列的步骤进行计算,进而可得数学期望.
【详解】(1)将得分为50分记为事件A;得分为50分即在六个问题的结果中,有五
个满意,一个不满意,
可能的结果共有: (种)
三名顾客产生的反馈结果总共有: (种)
则 ,∴购物中心得分为50分的概率为
(2)将顾客丙投出一个不满意记为事件B,则
, ,
(3) 可能的取值为2、3、4、5、6
,
,
2 3 4 5 6
∵ ,∴ .
20.已知椭圆C: 的离心率为 ,椭圆C的左、右顶点分别为A、B,直线l: 经过椭圆C的右焦点F,且与椭圆交于M,N两点.
(1)求椭圆C的标准方程;
(2)设直线BM,AN的斜率分别为 , ,若 ,求证:λ为定值.【答案】(1) ;
(2)证明见解析.
【分析】(1)由题可得 , ,即求;
(2)联立直线方程与椭圆方程,利用韦达定理法即求.
【详解】(1)由题意知右焦点F(1,0), ,又 ,
则 , ,
所以椭圆的标准方程为: ;
(2)设 , ,
由 可得 ,
则 , ,
又 ,B(2,0), ,
法一: ,由 得 ,
∴
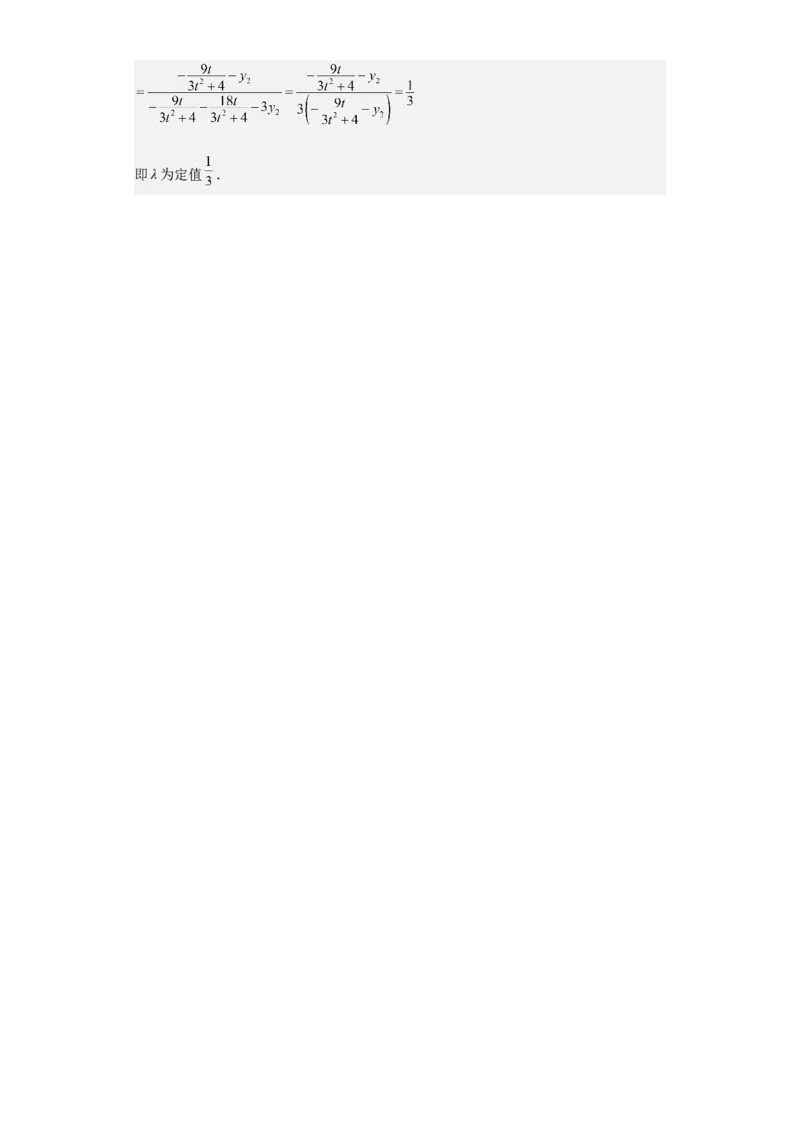
即λ为定值 .
法二:即λ为定值 .21.已知函数 .
(1)求函数 在 处的切线方程;
(2)若不等式 恒成立,求实数 的取值范围.
【答案】(1)
(2)
【分析】(1)根据切点和斜率求得切线方程.
(2)由 分离常数 ,通过构造函数法,结合导数来求得 的取值范
围.
(1)
的定义域为 ,
,则 ,
,故切线方程为 ,
即 .
(2)
恒成立,其中 ,所以 ,
记 ,
则 ,
当 时, ;当 时, ,
所以 在 单调递减,在 单调递增, ,
则实数 的取值范围为 .
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所
做的第一题计分.
22.[选修4-4:坐标系与参数方程](10分)已知直线 ( 为参数),以坐标原点为极点, 轴的正半轴为极轴建立
极坐标系,曲线 的极坐标方程为 .
(1)将曲线C的极坐标方程化为直角坐标方程;(2)设点 的直角坐标为 ,直线 与曲线C 的交点为 , ,求 的值.
【答案】(1) ;(2) .
【详解】试题分析:(1)在方程 两边同乘以极径 可得 ,再根
据 ,代入整理即得曲线 的直角坐标方程;(2)把直线的参数
方程代入圆的直角坐标方程整理,根据韦达定理即可得到 的值.
试题解析:(1) 等价于 ①
将 代入①既得曲线C的直角坐标方程为
,②
(2)将 代入②得 ,
设这个方程的两个实根分别为
则由参数t 的几何意义既知, .
考点:圆的极坐标方程与直角坐标方程的互化及直线参数方程的应用.
23.[选修4-5:不等式选讲](10分)
已知函数 .
( )求不等式 的解集;
1
( )若关于 的不等式 有解,求实数 的取值范围.
2
【答案】(1) (2)m≤﹣ 或m≥1.
【详解】试题分析:
(Ⅰ)零点分段可得不等式的解集为{x|- };
(Ⅱ)由题意得到关于实数m的不等式,求解不等式可得实数m的取值范围是m≤﹣ 或m≥1.
试题解析:
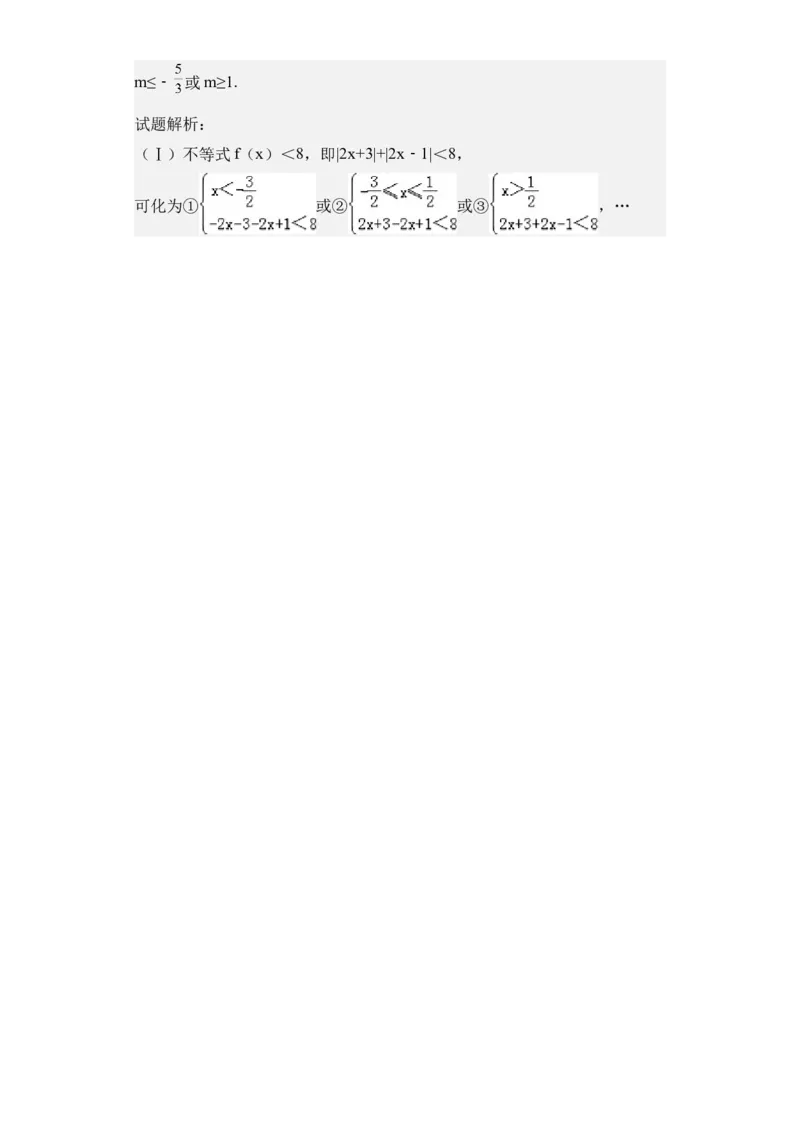
(Ⅰ)不等式f(x)<8,即|2x+3|+|2x﹣1|<8,
可化为① 或② 或③ ,…解①得﹣ <x<﹣ ,解②得﹣ ≤x≤ ,解③得 <x< ,
综合得原不等式的解集为{x|- }.
(Ⅱ)因为∵f(x)=|2x+3|+|2x﹣1|≥|(2x+3)﹣(2x﹣1)|=4,
当且仅当﹣ ≤x≤ 时,等号成立,即f(x) =4,…
min
又不等式f(x)≤|3m+1|有解,则|3m+1|≥4,解得:m≤﹣ 或m≥1.公众号:高中试卷君