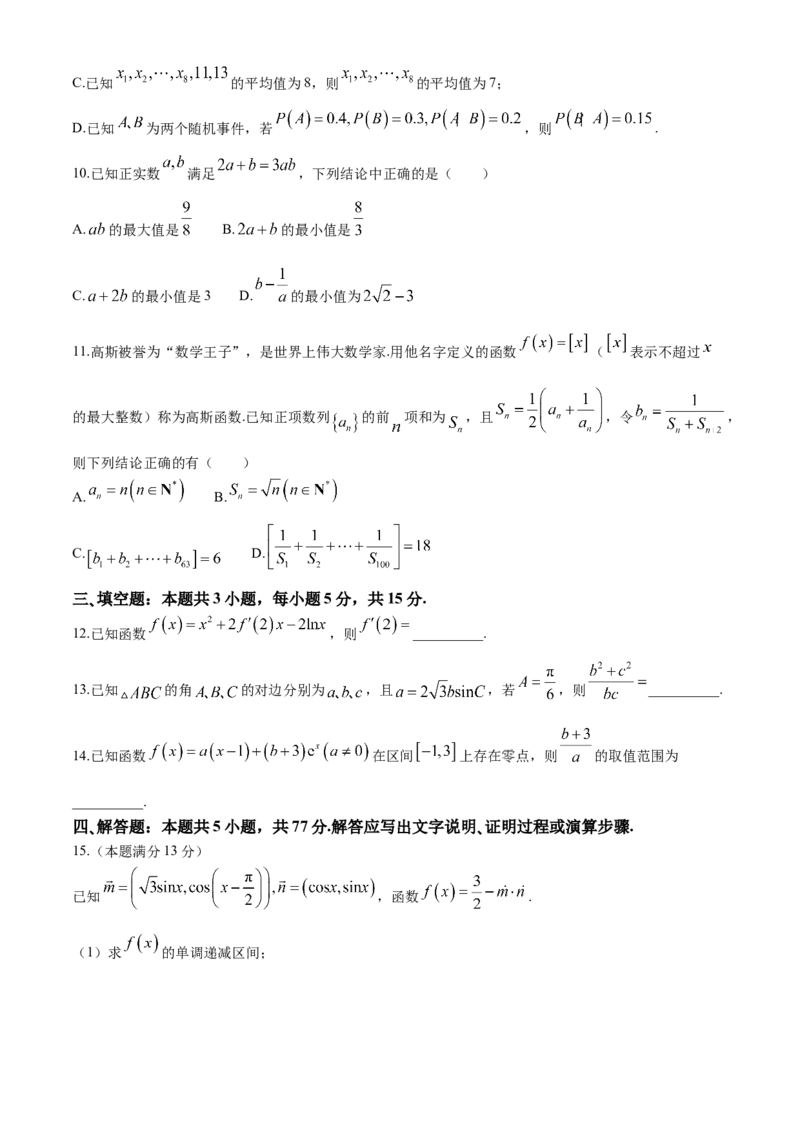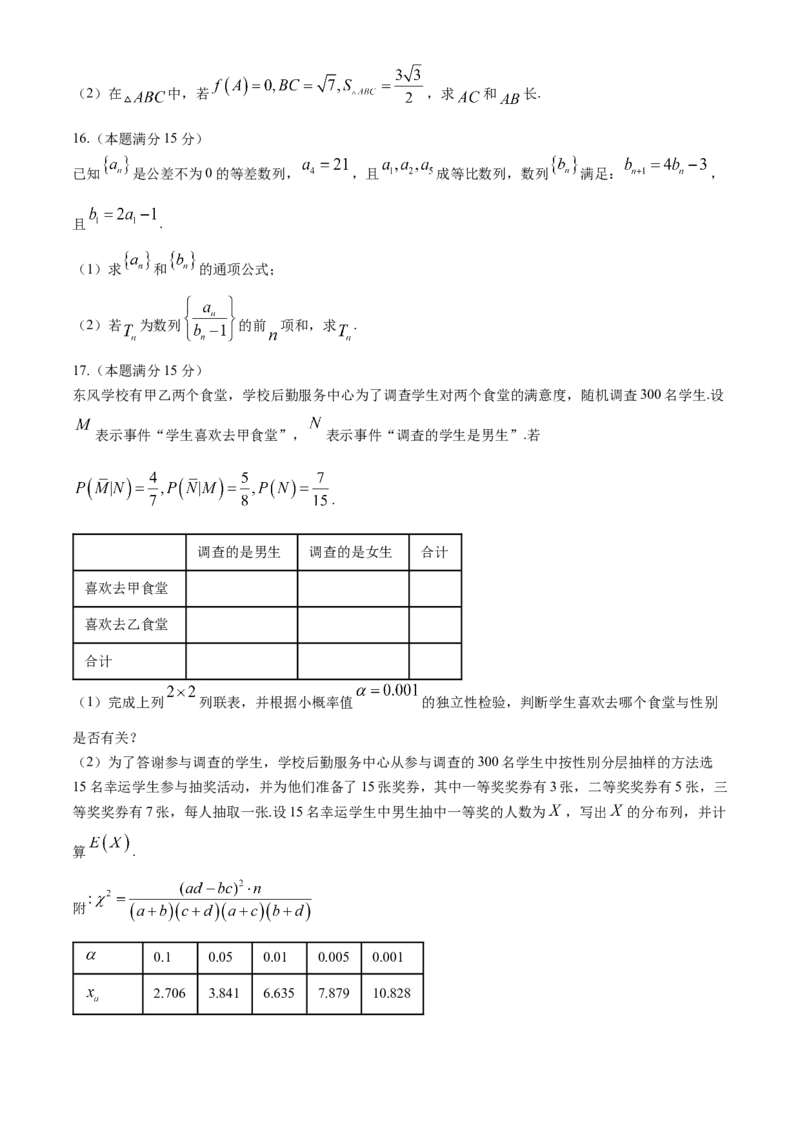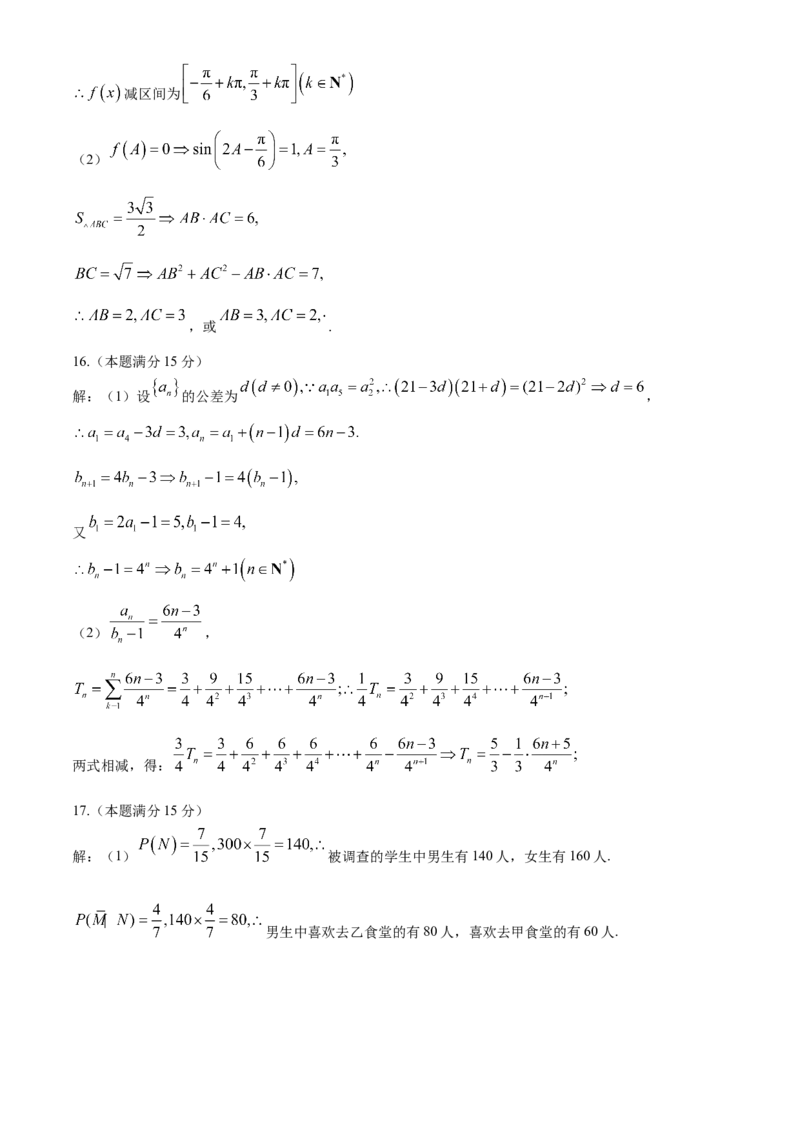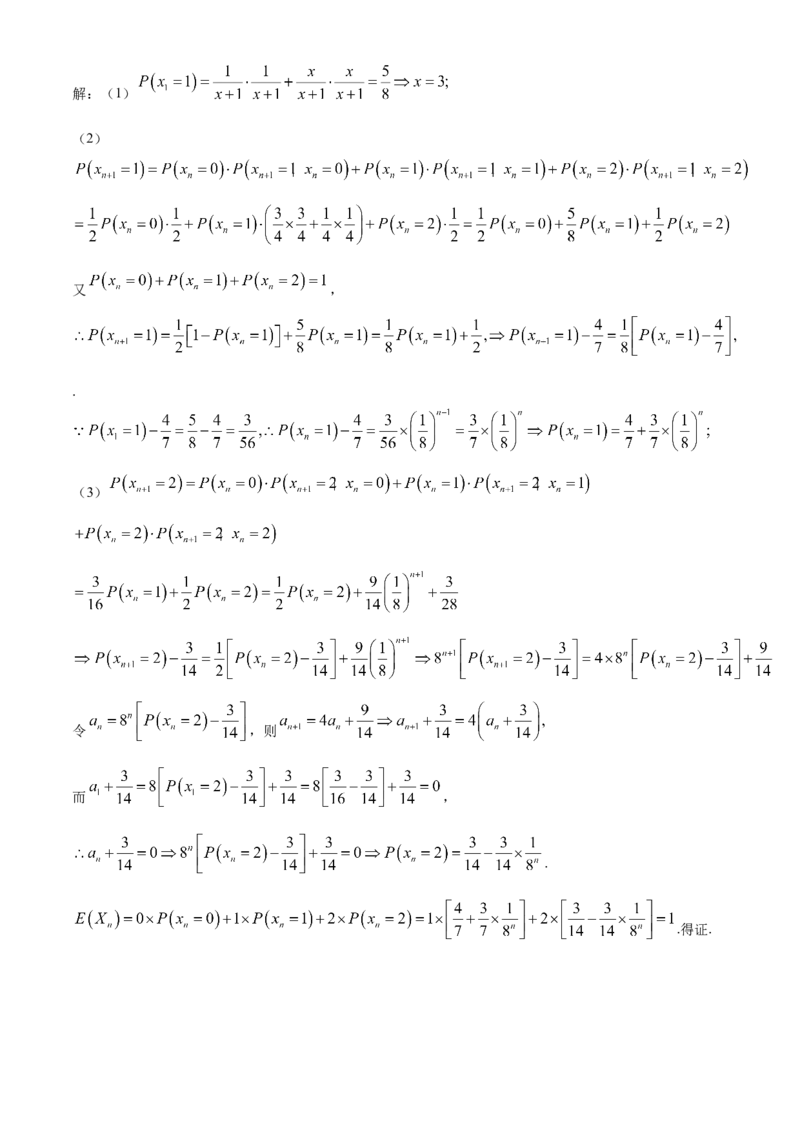文档内容
2024 年秋季普通高中 11 月份高三年级阶段性联考
数学
本试卷共4页,19题.全卷满分150分.考试用时120分钟.
★祝考试顺利★
注意事项:
1.答题前,先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上,并将准考证号
条形码粘贴在答题卡上的指定位置.
2选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.写在试
卷、草稿纸和答题卡上的非答题区域均无效.
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答
题卡上的非答题区域均无效.
4.考试结束后,请将答题卡上交.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.在复平面内,复数 对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.已知 ,则 的值为( )
A. B. C. D.
3.已知 ,且 ,则 与 的夹角为( )
A. B. C. D.
4.已知曲线 在点 处的切线在 轴上的截距为 ,则 的值为( )
A.1 B.0 C. D.
5.暑假期间某校5名学生计划去黄冈旅游,体验黄冈的风俗与文化.现有黄梅东山问梅村、罗田天堂寨、黄州
的东坡赤壁三个景区可供选择若每名学生只去一个景区,且恰有2人前往黄梅东山问梅村,则不同的游览
方案种数为( )
A.40 B.90 C.80 D.1606.已知函数 的最小正周期为 ,将 的图象向右平移 个单位后得
到函数 的图象,若 为偶函数,则正实数 的最小值为( )
A. B. C. D.
7英国生物统计学家高尔顿设计了高尔顿钉板来研究随机现象.如图是一个高尔顿钉板的设计图,每一黑点
表示钉在板上的一颗钉子,它们彼此的距离均相等,上一层的每一颗钉子恰好位于下一层两颗打子的正中
间,小球每次下落,将随机的向两边等概率的下落.数学课堂上,老师向学生们介绍了高尔顿钉板放学后,
爱动脑的小明设计了一个不一样的“高尔顿钉板”,它使小球在从钉板上一层的两颗钉子之间落下后砸到
下一层的钉子上时,向左下落的概率为向右下落的概率的2倍.当有大量的小球依次滚下时,最终都落入钉
板下面的5个不同位置.若一个小球从正上方落下,经过5层钉板最终落到4号位置的概率是( )
A. B. C. D.
8. 是定义在 上的函数, 为 的导函数,若方程 在 上至少有3个
不同的解,则称 为 上的“波浪函数”.已知定义在 上的函数 为
“波浪函数”,则实数 的取值范围是( )
A. B.
C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项是符
合题目要求.全部选对的得6分,部分选对得部分分,有错选的得0分.
9.下列结论中正确的有( )
A.已知 ,若 ,则 ;
B.某学生8次考试的数学成绩分别为:101、108、109、120、132、135、141、141,则这8次数学成绩的第75百
分位数为135;C.已知 的平均值为8,则 的平均值为7;
D.已知 为两个随机事件,若 ,则 .
10.已知正实数 满足 ,下列结论中正确的是( )
A. 的最大值是 B. 的最小值是
C. 的最小值是3 D. 的最小值为
11.高斯被誉为“数学王子”,是世界上伟大数学家.用他名字定义的函数 ( 表示不超过
的最大整数)称为高斯函数.已知正项数列 的前 项和为 ,且 ,令 ,
则下列结论正确的有( )
A. B.
C. D.
三、填空题:本题共3小题,每小题5分,共15分.
12.已知函数 ,则 __________.
13.已知 的角 的对边分别为 ,且 ,若 ,则 __________.
14.已知函数 在区间 上存在零点,则 的取值范围为
__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题满分13分)
已知 ,函数 .
(1)求 的单调递减区间;(2)在 中,若 ,求 和 长.
16.(本题满分15分)
已知 是公差不为0的等差数列, ,且 成等比数列,数列 满足: ,
且 .
(1)求 和 的通项公式;
(2)若 为数列 的前 项和,求 .
17.(本题满分15分)
东风学校有甲乙两个食堂,学校后勤服务中心为了调查学生对两个食堂的满意度,随机调査300名学生.设
表示事件“学生喜欢去甲食堂”, 表示事件“调査的学生是男生”.若
.
调查的是男生 调查的是女生 合计
喜欢去甲食堂
喜欢去乙食堂
合计
(1)完成上列 列联表,并根据小概率值 的独立性检验,判断学生喜欢去哪个食堂与性别
是否有关?
(2)为了答谢参与调查的学生,学校后勤服务中心从参与调查的300名学生中按性別分层抽样的方法选
15名幸运学生参与抽奖活动,并为他们准备了15张奖券,其中一等奖奖券有3张,二等奖奖券有5张,三
等奖奖券有7张,每人抽取一张.设15名幸运学生中男生抽中一等奖的人数为 ,写出 的分布列,并计
算 .
附
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.82818.(本题满分17分)
已知函数 .
(1)讨论 的单调性;
(2)当 时, 恒成立,求实数 的取值范围;
(3)证明: .
19.(本题满分17分)
马尔科夫链是一种随机过程,它具有马尔科夫性质,也称为“无记忆性”,即一个系统在某时刻的状态仅
与前一时刻的状态有关.为了让学生体验马尔科夫性质,数学老师在课堂上指导学生做了一个游戏.他给小
明和小美各一个不透明的箱子,每个箱子中都有 个红球和1个白球,这些球除了颜色不同之外,其他的
物质特征完全一样规定“两人同时从各自的箱子中取出一个球放入对方的箱子中”为一次操作,假设经过
次操作之后小明箱子里的白球个数为随机变量 ,且 .
(1)求 的值;
(2)求 ;
(3)证明: 为定值.2024 年秋季普通高中 11 月份阶段性联考高三数学试卷
参考答案
一、选择题:本题共8小题,每小题5分,共40分.
1.D 2.B 3.B 4.C 5.C 6.B 7.A 8.D
8.【解析】,
显然 不满足上式,所以 ,
令 ,则 ,
在 ,
且 ,
画出的图像,可知: .
二、选择题(多选)【有错选得0分,全对得6分,部分对得部分分.两解题,每答对一个得3
分,三解题,每答对一个得2分】
9.ACD 10.BCD 11.BCD
10.解析:(1) (当 时取等号);
(2) (当 时取等号);
(3) (当
时取等号);
(4) (当 时取等号).
11.解析:(1) 当 时, ,又
A错,B对;
(2)
,.故C对;
(3) ,
当 时, ,
,
;故D对;
三、填空题:
12. 13. 14.
14.【解析】
,令 ,
在 ,在 ,
作出 的图像,可知: .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题满分13分)
解:(1)
由减区间为
(2)
,或 .
16.(本题满分15分)
解:(1)设 的公差为 ,
又
(2) ,
两式相减,得:
17.(本题满分15分)
解:(1) 被调查的学生中男生有140人,女生有160人.
男生中喜欢去乙食堂的有80人,喜欢去甲食堂的有60人..被调查的学生中喜欢去甲食堂的有160人.
调查的是 调查的是
合计
男生 女生
喜欢去
60 100 160
甲食堂
喜欢去
80 60 140
乙食堂
合计 140 160 300
零假设 :假设学生喜欢去哪个食堂与性别无关.
,
根据小概率值 的独立性检验,我们推断 不成立,即认为学生喜欢去哪个食堂与性别有关.此
推断犯错误的概率不大0.001.
(2)根据男女生人数之比可知,被抽取的15人中男生7人,女生8人.
,
,
X的分布列为:
X 0 1 2 3
p
,
18.(本题满分17分)
解(1)定义域为 ;
.
.当 时, 恒成立, ;
.当 时, 有两根,但两根均为负数,当 时,
.当 时, 有两正根 和 ,
当 时, ;当 时, ;
当 时 ;
综上所述:
.当 时, 增区间为 ;
.当 时, 增区间为 和 ;减区间为
.
(2) ,令 ,则 在
,
若 ,则 ,与题意相符;
若 ,则 ,所以必存在 ,使得当 时, ,
从而使得当 时, ,与题意相矛盾;
综上: .
(3)证明:由(2)知,当 时, (仅当 时取等号),
,令 ,则有: ;
,得证.
19.(本题满分17分)解:(1)
(2)
又 ,
.
(3)
令 ,则
而 ,
.
.得证.