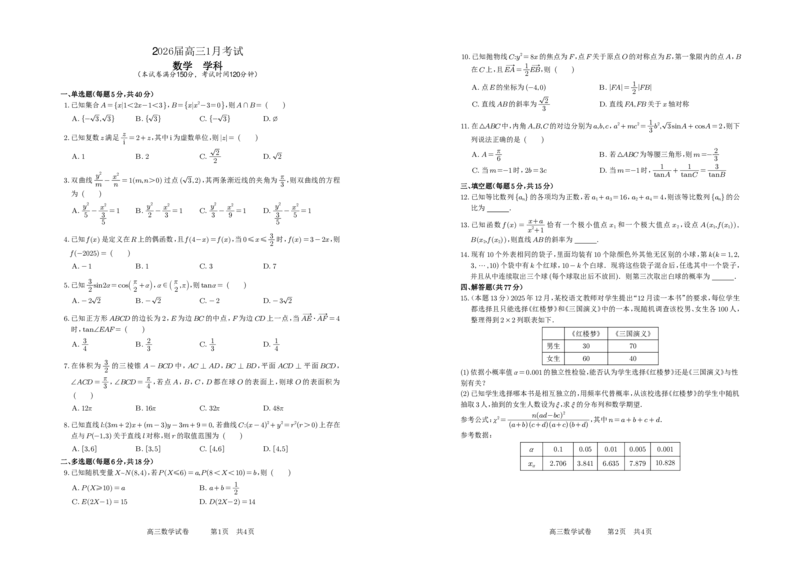文档内容
3 3 3 3
z
i
2
2
2
x π
3
n 3
x x x x
5 3 2 3 3 9 3 5
5 5
3
2
3
2
2 2 2
3 2 1 1
4 3 3 4
3
2
π π
3 4
1
2
D.D2X-2 =14
高三数学试卷 第1页 共4页
A.PX≥10 =a
C. E2X-1 =15
9.已知随机变量X~N8,4 ,若PX≤6 =a,P(80)上存在
点与P(-1,3)关于直线l对称,则r的取值范围为 ( )
A. 3,6
f-2025 = ( )
A.-1 B.1 C.3 D.7
5.已知 sin2α=cos
fx =3-2x,则 4.已知fx 是定义在R上的偶函数,且f4-x =fx ,当0≤x≤ 时,
3.双曲线 ,2 ,其两条渐近线的夹角为 ,则双曲线的方程
m
为 ( )
y2 2 y2 2 y2 2 y2 2
A. - =1 B. - =1 C. - =1 D. - =1
=1m,n>0 过点
=2+z,其中i为虚数单位,则z = ( )
A.1 B.2 C. D.
y2 2
-
D.∅
2.已知复数z满足
C. - B.
1.已知集合A=x1<2x-1<3 ,B=xx2-3=0 ,则A∩B= ( )
A. - ,
2026届高三1月考试
10.已知抛物线C:y2=8x的焦点为F,点F关于原点O的对称点为E,第一象限内的点A,B
数学 学科 1
(本试卷满分150分,考试时间120分钟) 2
1
2
一、单选题(每题5分,共40分)
2
3
1
3
3
π 2
6 3
1 1 3
tanA tanC tanB
x+a
2+
Bx 2 ,fx 2 ,则直线AB的斜率为 .
14.现有10个外表相同的袋子,里面均装有10个除颜色外其他无区别的小球,第k(k=1,2,
3,⋯,10)个袋中有k个红球,10-k个白球.现将这些袋子混合后,任选其中一个袋子,
并且从中连续取出三个球(每个球取出后不放回).则第三次取出白球的概率为 .
四、解答题(共77分)
15.(本题13分)2025年12月,某校语文教师对学生提出“12月读一本书”的要求,每位学生
都选择且只能选择《红楼梦》和《三国演义》中的一本,现随机调查该校男、女生各100人,
整理得到2×2列联表如下.
《红楼梦》 《三国演义》
男生 30 70
女生 60 40
(1)依据小概率值α=0.001的独立性检验,能否认为学生选择《红楼梦》还是《三国演义》与性
别有关?
(2)已知学生选择哪本书是相互独立的,用频率代替概率,从该校选择《红楼梦》的学生中随机
抽取3人,抽到的女生人数设为ξ,求ξ的分布列和数学期望.
n(ad-bc)2
参考公式:χ2= ,其中n=a+b+c+d.
(a+b)(c+d)(a+c)(b+d)
参考数据:
α 0.1 0.05 0.01 0.005 0.001
x 2.706 3.841 6.635 7.879 10.828
α
高三数学试卷 第2页 共4页
恰有一个极小值点x 1 和一个极大值点x 2 ,设点Ax 1 ,fx 1 , 13.已知函数 fx = x 1
三、填空题(每题5分,共15分)
12.已知等比数列a 的各项均为正数,若a +a =16,a +a =4,则该等比数列a 的公
n 1 3 2 4 n
比为 .
在C上,且EA= EB,则 ( )
A.点E的坐标为(-4,0) B.|FA|= |FB|
C.直线AB的斜率为 D.直线FA,FB关于x轴对称
11.在△ABC中,内角A,B,C的对边分别为a,b,c,a2+mc2= b2, sinA+cosA=2,则下
列说法正确的是 ( )
A.A= B.若△ABC为等腰三角形,则m=-
C.当m=-1时,2b=3c D.当m=-1时, + =16.(本题15分)已知函数fx
1+lnx
= .
x
(1)求fx 的单调性;
(2)若eax-1+ax-x≥xfx 对任意x∈0,+∞ 恒成立,求实数a的取值范围.
17.(本题15分)如图,在四棱锥P-ABCD中,PA⊥PD,△PAB为等边三角形,四边形
ABCD为直角梯形,AB⎳CD,AB⊥BC,AB=2CD=2.
(1)证明:PB⊥PD;
π
(2)若直线PD与平面ABCD所成的角为 .求平面PAD和平面ADC所成角的余弦值.
4
x2 y2 3
18.(本题17分)已知椭圆C: + =1(a>b>0),四点P-1,
a2 b2 1 2
3
,P1,
2 2
,P(0, 3),P
3 4
(1, 3)中恰有三点在椭圆C上.
(1)求椭圆C的方程;
(2)过点D4,0 且斜率不为0的直线l与椭圆C相交于M,N两点.
(i)若O为原点,求△MON面积的最大值;
(ii)点A-2,0 ,设点Q是线段MN上异于M,N的一点,直线QA,QM的斜率分别为k,k , 1 2
DM
且k +k =0,求
1 2
⋅NQ
DN ⋅MQ
S S 1
19.(本题17分)已知数列{a }的前n项和为S ,且满足a =1, n-1 - n-1 + =0(n≥2).
n n 1 a a 2
n n-1
(1)求{a }的通项公式;
n
(2)当n≥3时,已知f(x)=(x-a)(x-a )⋯(x-a )的导函数为
1 2 n
f'(x)=n(x-b)(x-b )⋯(x-b ).
1 2 n-1
n uv
其中b ≤b ≤⋯≤b .令F(u,v)= .
1 2 n-1 (j-i+u)(j-i-v)
i=1
(i)设u =b -j,v =j-b (2≤j≤n-1),证明:F(u,v)=0;
j j j j-1 j j
(ii)证明:对任意2≤j≤n-1,有b -b >1.
j j-1
的值.
高三数学试卷 第3页 共4页 高三数学试卷 第4页 共4页