数学试卷-2026年沈阳市高中三年级教学质量监测(一)(1)_2026年1月_260117辽宁省沈阳市2026届高中三年级高三教学质量监测（一）（沈阳一模）（全科）

2026 年沈阳市高中三年级教学质量监测（一） 数 学 命题：沈阳市第一二〇中学 潘 戈 沈阳市第四中学 张大海 东北育才学校 徐滨滨 主审：沈阳市教育研究院 王孝宇 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。考生作答时，将答案写在答题卡上，在本 试卷上答题无效。考试结束后，将本试卷和答题卡一并交回。 注意事项： 1.答题前，考生务必将自己的姓名、考号填写在答题卡上，并将条码粘贴在答题卡指定的区域内。 2.第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动用橡皮擦干净后， 再选涂其他答案标号。第Ⅱ卷用黑色墨水签字笔在答题卡指定位置书写作答，在本试题卷上作答无效。 3.考试结束后，考生将答题卡交回。 第Ⅰ卷（选择题共 58 分） 一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要 求的。 1．已知集合U {x|1x6，xN}，A{2，3}，B{2，4，5}，则(ð A)B( ) U A．{4，5} B．{2，3，4，5} C．{2} D．{2，4，5} a3i 2．若复数 是纯虚数，则实数a( ) 2i 3 3 2 2 A． B． C． D． 2 2 3 3 x1 3. 不等式 1的解集( ) 3x A．[1，3] B．[1，3) C．(，1] D．[1，3)(3，) 4．样本数据5，7，4，6，12，10，11，9的第70百分位数为( ) A．7 B．9 C．9.5 D．10 x2 y2 5．抛物线y2 2px(p0)的焦点与双曲线  1的右焦点重合，则抛物线准线方程为( ) 16 9 5 5 A．x10 B．x C．x5 D．x 2 4 第1页共4页6．若函数y f(x)是yax (a0且a1)的反函数，则函数y f(2x1)3图象必过定点( ) 1 1 A．( ，4) B．(1，4) C．( ，3) D．(1，3) 2 2 7．已知在圆x2  y2 4x2y0内，过点E(1，0) 的最长弦和最短弦分别是AC 和BD，则四边形ABCD的 面积为( ) A．3 5 B．6 5 C．2 15 D．4 15 8．如果方程F(x，y)0能确定y是x的函数，那么称这种方式表示的函数是隐函数，隐函数的求导方法 如下：在方程F(x，y)0中，把y看成x的函数y y(x)，则方程可看成关于x的恒等式F(x，y(x))0， 在等式两边同时对x求导，然后解出y(x)即可. 例如，求由方程x2  y2 1所确定的隐函数的导数y，将方 程x2  y2 1的两边同时对x求导，则2x2yy0(y y(x) 是中间变量，需要用复合函数的求导法则）， x 得y (y0)，那么曲线xylny2在点(2，1)处的切线方程为( ) y A．x3y10 B．x3y50 C．3x y50 D．2x3y70 二、多选题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合题目要求。全部 选对的得6分，部分选对的得部分分，有选错的得0分。 9．下列结论正确的是( ) 1 A．若x1，则函数y x 的最小值为3 x1 B．若x2y3，则2x 4y的最小值为4 2 2 1 C．函数y  的最小值为32 2 sin2x cos2x 1 D．若x0，y0，且x2y2，则xy的最大值为 2 10．已知事件A，B满足P(A) 0.5，P(B) 0.2，则下列结论正确的是( ) A．若B A，则P(AB)0.5 B．若A与B互斥，则P(AB)0.7 C．若P(AB)0.1，则A与B相互独立 D．若A与B相互独立，则P(AB)0.9 11．已知数列{a }的前n项和为S ，若a 2，a 2a a a 0，则下列结论正确的是( ) n n 1 n1 n n n1 9 1 A．a  B．数列{1 }为等比数列 3 7 a n 23 1 C．a a D．S   n1 n 10 2 210 第2页共4页第 II 卷(非选择题共 92 分) 三、填空题：本题共3小题，每小题5分，共15分。  12. 在ABC 中，角 A， B ，C 的对边分别为a，b，c ，若sinAsinBcosC 且c2 3 ， A ，则 6 ca =________. sinCsinA a 13．已知a0，二项式(x )6的展开式中所有项的系数和为64，则展开式中的常数项为 ________. x2 14．已知球O内切于正四棱台（即球与该正四棱台的上、下底面以及侧面均相切），且该正四棱台的上、下 底面棱长之比为1:2，则球O与该正四棱台的体积之比为________. 四、解答题：本题共5小题，共77分，解答应写出文字说明、证明过程或演算步骤。 15．（本题满分13分）已知数列{a }是公差为2的等差数列，其前8项和为64，数列{b }是公比大于0的等 n n 比数列b 3，b b 18. 1 3 2 （1）求数列{a }，{b }的通项公式； n n a （2）记c  n （nN，n1），求数列{c }的前n项和S . n b n n n     16．（本题满分15分）a (2 3cosx，1)，b (sinx，cos2x)且f(x)ab （1）求函数y f(x)的最小正周期；   （2）将函数y f(x)图象上所有的点向左平移 个单位后得到函数y g(x)的图象，当x[0， ]时，求 6 2 函数y g(x)的值域； （3）说明函数ysinx的图象经过怎样的变换能得到函数y f(x)的图象，写出一个变换过程. 17．（本题满分15分）如图，四棱锥P ABCD的底面ABCD是菱形，PD平面ABCD， PDCDBD2，E为PC的中点． （1）证明：PA平面BDE； （2）求三棱锥PBDE的体积； 3 21 （3）在棱AP上是否存在一点F ，使得二面角F BDE正弦值为 ？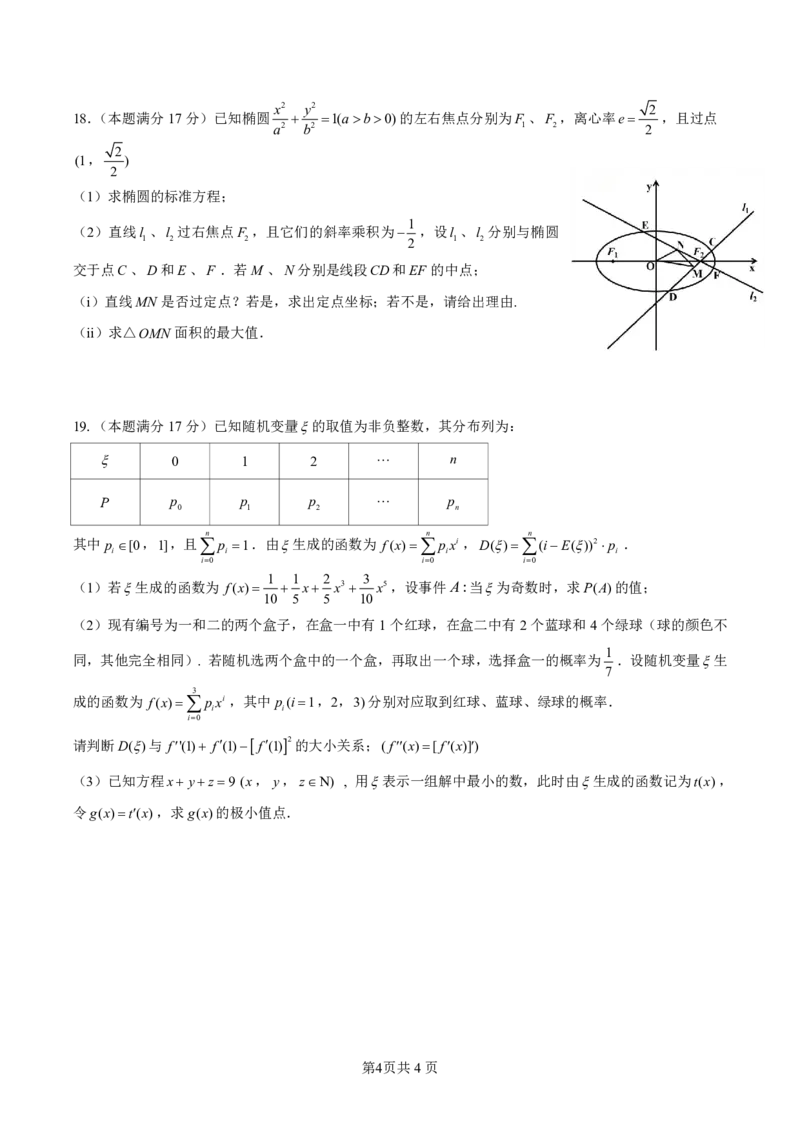若存在，求出 14 AF 的长；若不存在，请说明理由． 第3页共4页x2 y2 2 18．（本题满分17分）已知椭圆  1(ab0)的左右焦点分别为F 、F ，离心率e ，且过点 a2 b2 1 2 2 2 (1， ) 2 （1）求椭圆的标准方程； 1 （2）直线l 、l 过右焦点F ，且它们的斜率乘积为 ，设l 、l 分别与椭圆 1 2 2 2 1 2 交于点C、D和E、F ．若M 、N分别是线段CD和EF 的中点； （i）直线MN 是否过定点？若是，求出定点坐标；若不是，请给出理由. （ii）求△OMN 面积的最大值． 19.（本题满分17分）已知随机变量的取值为非负整数，其分布列为：  0 1 2  n  P p p p p 0 1 2 n n n n 其中 p [0，1]，且p 1．由生成的函数为 f(x)pxi ，D()(iE())2p ． i i i i i0 i0 i0 1 1 2 3 （1）若生成的函数为 f(x)  x x3  x5，设事件 A:当为奇数时，求P(A)的值； 10 5 5 10 （2）现有编号为一和二的两个盒子，在盒一中有1个红球，在盒二中有2个蓝球和4个绿球（球的颜色不 1 同，其他完全相同）. 若随机选两个盒中的一个盒，再取出一个球，选择盒一的概率为 ．设随机变量生 7 3 成的函数为 f(x)pxi ，其中 p(i1，2，3)分别对应取到红球、蓝球、绿球的概率． i i i0 请判断D()与 f'(1) f(1)f(1)2的大小关系；(f(x)[f(x)]) （3）已知方程x yz9 (x，y，zN) , 用表示一组解中最小的数，此时由生成的函数记为t(x)， 令g(x)t(x)，求g(x)的极小值点． 第4页共4页