数学解析-2026年沈阳市高中三年级教学质量监测(一)(1)_2026年1月_260117辽宁省沈阳市2026届高中三年级高三教学质量监测（一）（沈阳一模）（全科）

2026 年沈阳市高中三年级教学质量监测（一） 数 学 本试卷共4页，19小题，满分150分，答题用时120分钟。 注意事项： 1.答题前，先将自己的姓名、考号填写在答题卡上，并将条码粘贴在答题卡指定 区域。 2.选择题的作答：每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标 号涂黑，如需改动用橡皮擦干净后，再选涂其他答案标号。 3.填空题和解答题的作答：用黑色墨水签字笔在答题卡指定位置书写作答，写在 答题卡上的非答题区域无效。 4.必须保持答题卡的整洁。考试结束后，请将答题卡交回。 一、选择题：本题共8小题，每小题 5分，共 40 分。在每小题给出的四个选项 中，只有一项是符合题目要求的。 1. 已知集合U  x1 x6,xN  ，A2,3，B2,4,5，则  ð A B（ ） U A．4,5 B．2,3,4,5 C．2 D．2,4,5 a3i 2. 若复数 是纯虚数，则实数a（ ） 2i 3 3 2 2 A． B． C． D． 2 2 3 3 x1 3. 不等式 1的解集（ ） 3x A． 1,3  B． 1,3 C．,1  D． 1,3  3, 4. 样本数据5，7，4，6，12，10，11，9的第70百分位数为（ ） A．7 B．9 C．9.5 D．10 5. 抛物线y2 2pxp0的焦点与双曲线 x2  y2 1的右焦点重合，则抛物线准线方程为 16 9 （ ）． 5 5 A．x10 B．x C．x5 D．x 2 4 16. 若函数 y f  x 是yax a0且a1 的反函数，则函数y f  2x1 3的图像必过定 点（ ） 1  1  A． ,4 B． 1,4  C． ,3 D． 1,3  2  2  7. 已知在圆M :x2 y24x2y0内，过点E1,0的最长弦和最短弦分别是AC和BD， 则四边形ABCD的面积为( ) A．3 5 B． 6 5 C．2 15 D．4 15 8. 如果方程F(x,y)0能确定y是x的函数，那么称这种方式表示的函数是隐函数．隐函 数的求导方法如下：在方程F(x,y)0中，把y看成x的函数y yx，则方程可看成 关于x的恒等式F  x,yx0，在等式两边同时对x求导，然后解出yx即可．例如， 求由方程x2y2 1所确定的隐函数的导数y，将方程x2y2 1的两边同时对x求导， 则2x2yy0（y y(x)是中间变量，需要用复合函数的求导法则），得 x y (y0)．那么曲线xylny2在点2,1处的切线方程为（ ） y A．x3y10 B．x3y50 C．3xy50 D．2x3y70 二、选择题：本题共 3小题，每小题 6分，共 18 分．在每小题给出的四个选项 中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的 得0分． 9. 下列说法正确的是（ ） 1 A．若x1，则函数yx 的最小值为3 x1 B．若x2y 3，则2x4y的最小值为 4 2 2 1 C．函数 y  的最小值为32 2 sin2x cos2x 1 D．若x0,y0，且x2y2，则xy  max 2 10. 已知事件A，B满足P(A)0.5，P(B)0.2，则下列结论正确的是( ). A．若B A，则P(AB)0.5 2B．若A与B互斥，则P(AB)0.7 C．若P(AB)0.1，则A与B相互独立 D．若A与B相互独立，则P(AB)0.9 11. 已知数列a 的前n项和为S ，若a 2，a 2a a a 0，则（ ） n n 1 n1 n n n1 9  1  A．a  B．数列1 为等比数列 3 7  a  n 23 1 C．a a D．S   n1 n 10 2 210 三、填空题：本题共3小题，每小题5分，共15分。 π 12. 在ABC中，角A，B，C的对边分别为a，b，c，若sinAsinBcosC且c2 3，A ， 6 ca 则 _______ sinCsinA 6  a  13. 已知a0，二项式 x  的展开式中所有项的系数和为64，则展开式中的常数项为  x2  _______ 14. 已知球O内切于正四棱台（即球与该正四棱台的上、下底面以及侧面均相切），且该 正四棱台的上、下底面棱长之比为1:2，则球O与该正四棱台的体积之比为_______ 四、解答题：本题共 5小题，共 77分，解答应写出文字说明、证明过程或演算 步骤。 15. 已知数列a 是公差为2的等差数列，其前8项的和为64．数列b 是公比大于0的 n n 等比数列，b 3,b b 18． 1 3 2 (1)求数列a 和b 的通项公式； n n a (2)记c  n ，nN*，求数列c 的前n项和S ； n b n n n 316. 已知a    2 3cosx,1  ,b   sinx,cos2x 且 f xa  b  . (1)求函数y f x的最小正周期； (2)将函数 f x图象上所有的点向左平移 π 个单位后，得到函数gx的图象，当x   0, π  时， 6  2 求函数gx的值域. (3)说明函数ysinx的图象经过怎样的变换能得到y f x函数的图象，写出一个 变换过程. 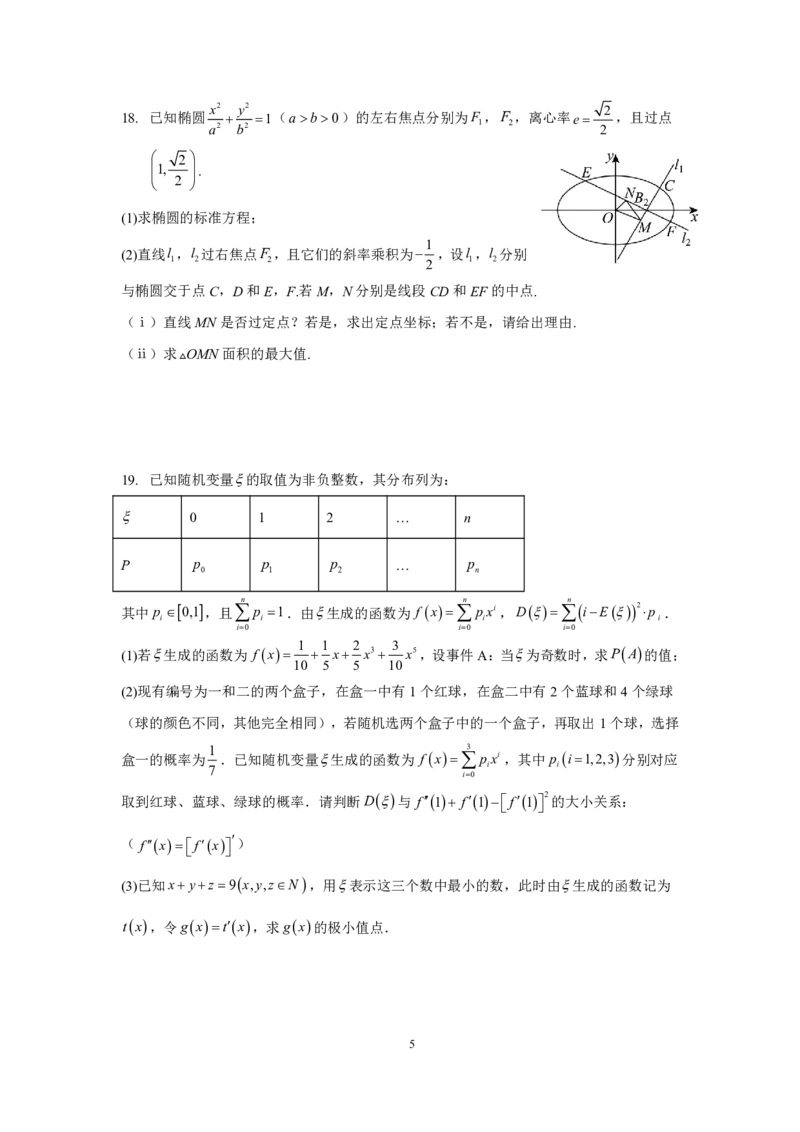17. 如图，四棱锥PABCD的底面ABCD是菱形，PD底面ABCD，PDCDBD2， E是PC的中点． (1)证明：PA//平面BDE； (2)求三棱锥PBDE的体积; 3 21 (3)在AP上是否存在一点F，使得二面角F BDE的正弦值为 ？若存在，求AF；若 14 不存在，请说明理由． 4x2 y2 2 18. 已知椭圆  1（ab0）的左右焦点分别为F ，F ，离心率e ，且过点 a2 b2 1 2 2  2 1, .    2  (1)求椭圆的标准方程； 1 (2)直线l ，l 过右焦点F ，且它们的斜率乘积为 ，设l ，l 分别 1 2 2 2 1 2 与椭圆交于点C，D和E，F.若M，N分别是线段CD和EF的中点. （ⅰ）直线MN是否过定点？若是，求出定点坐标；若不是，请给出理由. （ⅱ）求OMN 面积的最大值. 19. 已知随机变量的取值为非负整数，其分布列为：  0 1 2 … n P p p p … p 0 1 2 n n n n 其中 p  0,1 ，且p 1．由生成的函数为 f xpxi，D iE2 p ． i i i i i0 i0 i0 1 1 2 3 (1)若生成的函数为 f x  x x3 x5，设事件A：当为奇数时，求PA的值； 10 5 5 10 (2)现有编号为一和二的两个盒子，在盒一中有1个红球，在盒二中有2个蓝球和4个绿球 （球的颜色不同，其他完全相同），若随机选两个盒子中的一个盒子，再取出1个球，选择 1 3 盒一的概率为 ．已知随机变量生成的函数为 f xpxi，其中p i1,2,3分别对应 7 i i i0 取到红球、蓝球、绿球的概率．请判断D与 f1 f1 f1  2的大小关系： （ fx fx  ） (3)已知xyz9x,y,zN ，用表示这三个数中最小的数，此时由生成的函数记为 tx，令gxtx，求gx的极小值点． 52026 年沈阳市高中三年级教学质量监测（一）答案 单选：AABD CDCB 多选：BCD BC BCD  填空：4 15 7 1. 【答案】A 【分析】由全集U和集合A可求出ð A，再由交集运算性质即可求解. U 【详解】由题意得，U 2，3，4，5，又A2,3则ð A4,5， U 因为B2,4,5，所以  ð A B4,5， U 故选：A. 2. 【答案】A 【分析】利用除法运算化简复数，根据纯虚数的特征，即可判断. a3i (a3i)(2i) 2a3(6a)i 3 【详解】   ，则2a30，有a . 2i 5 5 2 故选：A 3. 【答案】B 【分析】通过移项通分，把分式不等式转化为整式不等式，解一元二次不等式即可. x1 x1 2x2 22x 【详解】由 1可得 10， 0，即 0 3x 3x 3x 3x   2x2  x3 0  ，解得1 x3. 3x0 所以不等式的解集为  1,3  故选：B 4. 【答案】D 【分析】由百分位数的求解方法计算即可. 【详解】该组数据从小到大排列为：4,5,6,7,9,10,11,12， 因为870%5.6，所以该组数据的第70百分位数为从小到大排列的第6个数，为10. 6故选：D 5. 【答案】C 【分析】先求双曲线的右焦点坐标，根据抛物线的焦点可求 p的值，再根据抛物线方程求其 准线方程. 【详解】对于双曲线：因为 a2 16 ，b2 9，所以c2 a2b2 25，所以c5. 所以双曲线的右焦点坐标为：5,0 . p 对于抛物线y2 2pxp0，因为焦点为5,0，即 5 p10. 2 p 所以其准线方程为：x 5. 2 故选：C 6. 【答案】 D 【分析】利用同底指数函数与对数函数互为反函数的性质. 【详解】因为yax a0且a1 与函数y f  x 互为反函数， 所以 f  x log x  a0且a1  a 所以y f  2x1 3log  2x1 3，令2x11，得x1，此时y3 a 所以函数y f  2x1 3的图像必过定点 1,3  故选：D 7. 【答案】C 【分析】圆内过定点的最长弦是直径，最短的弦是与最长弦垂直的弦. 【详解】圆的标准方程：x22y12 5 由题意可得：最长弦为直径：2 5 最短的弦是2 3 则四边形ABCD的面积为2 15 故选：C 78. 【答案】B 【分析】利用给定隐函数的导数求法确定斜率，再求出切线方程即可. 【详解】由给定定义得，对xylny2左右两侧同时求导， 1 可得yxy y0，将点2,1代入，得12y y0， y 1 1 1 解得y ，故切线斜率为 ，得到切线方程为y1 x2， 3 3 3 化简得方程为x3y50，故B正确. 故选：B 9. 【答案】BCD 【分析】根据基本不等式求解判断选项ABD，利用“1”的代换技巧求解最值判断C. 【详解】对于A，∵x1，∴x10， 1 1  1   1  ∴y x  x1 1  1x  12 1x  11 ， x1 x1  1x 1x 1 当且仅当1x ，即x0时，取得最大值1，故A错误； 1x 对于B， 2x 4y 2 2x4y 2 2x2y 4 2 ， 3 3 当且仅当x ， y 时，2x4y取到最小值为4 2，故B正确； 2 4 对于C，y 2  1    2  1    sin2xcos2x  sin2x cos2x sin2x cos2x 2cos2x sin2x 2cos2x sin2x 3  32  32 2 . sin2x cos2x sin2x cos2x 当且仅当tan2x 2时，取等号，故C正确； 1 对于D，当x0,y0，且x2y2时，2x2y2 x2y 2 2 xy ，∴xy ， 2 当且仅当x2y1，xy取最大值 1 ，故D正确. 2 故选：BCD 10. 【答案】BC 【分析】根据给定条件，结合概率的性质、互斥事件、相互独立事件的概率公式，逐项分析 判断即可. 8【详解】对于A，由B A，得PABP(B)0.2，A错误； 对于B，由A与B互斥，得PAB0.50.20.7，B正确； 对于C，由PAB0.10.50.2，得P(AB)P(A)P(B)，则A与B相互独立，C正确；   对于D，由A与B相互独立，得A， B 相互独立，则P AB P(A)P(B)0.50.80.4 ，D 错误. 故选：BC 11. 【答案】BCD 【分析】根据给定条件，利用构造法求出数列a 的通项公式，再逐项判断即可. n 1 1 1 1 【详解】数列a 中，a 2，a 2a a a 0，则a 0，    ， n 1 n1 n n n1 n a 2 a 2 n1 n 1 1 1 1 1  1  整理得1 = (1 )，而1  ，因此数列1 是首项、公比均为 1 的等比数列， a n+1 2 a n a 1 2  a n  2 B正确； 1 1 2n 1 1  ，解得a  1 ， a 2n n 2n1 2n1 a 8 对于A，a  ，A错误； 3 7 1 1 对于C，a a   0，则a a ，C正确； n1 n 2n11 2n1 n1 n 1 1 1 1 1 1 对于D，S 21 1 1 11   10 221 231 2101 22 23 210 1 1 (1 ) 4 29 23 1 11   ，D正确. 1 2 210 1 2 故选：BCD 12. 【答案】4 π 【分析】由sinBCsinBcosC可得cosBsinC0，求出C  ，利用正弦定理可得答案. 3 【详解】在ABC中，由sinAsinBcosC可得sinBCsinBcosC， 即sinBcosC+cosBsinC sinBcosC 9所以cosBsinC0，因为B,C0,π， 所以sinC0，且cosB0， π π π 所以B ，又A ，可得C  ， 2 6 3 ca c 2 3   4 由正弦定理可得 sinCsinA sinC 3 2 13. 【答案】15 【分析】先根据“所有项的系数和”求得a，然后利用二项式展开式的通项公式求得正确答案. 【详解】令x1，则可得所有项的系数和为1a6 64且a0，解得a1，  1  6  1  k ∵ x  的展开式中的通项T Ckx6k   Ckx63k,k 0,1,...,6，  x2 k1 6 x2 6 ∴当k 2时，展开式中的常数项为C2 15. 6 π 14. 【答案】 7 【分析】设出正四棱台上、下底面的棱长，则可借助正四棱台性质及体积公式表示出内切球 体积及正四棱台体积，即可得解. 【详解】如图为该几何体的轴截面，其中圆O是等腰梯形ABCD的内切圆， 设圆O与梯形的腰相切于点P，Q，与上、下底面分别切于点O ，O ， 1 2 不妨设正四棱台上、下底面的棱长为2a，4a， 则CO CPa，BO BP2a，BCBPPC3a， 1 2 故在直角梯形OO BC中，过点C作CEAB，垂足为E，所以EBa， 1 2 在Rt△CEB中， CE 3212a2 2a ，为棱台的高，也是球的直径， 104  3 8 2a3π 所以半径为 2a，所以球的体积为V  π 2a  ， 1 3 3 1 56 2 a3 棱台体积为V  2 2a2a2 4a 22a4a  ， 2 3   3 V π 故球与棱台的体积比为 1  . V 7 2 n1 15. 【答案】(1)a 2n1,b 3n (2)S 1 n n n 3n 【分析】(1)根据等差等比数列通项公式直接求解；(2)利用错位相减法求和；(3)利用裂项相 消求和. 【详解】（1）设公差为d，公比为q， 87 则由题可得数列a 的前8项的和8a  d 8a 28d 64， n 1 2 1 因为d 2，所以a 1，所以a 12(n1)2n1， 1 n 又因为b 3,b b bq2bq18， 1 3 2 1 1 所以q2q60解得q3或q2（舍）， 所以b 33n1 3n. n 2n1 （2）由（1）得c  ，所以S c c c ， n 3n n 1 2 n 1 3 2n1 1 1 3 2n1 即S    ， S    ， n 3 32 3n 3 n 32 33 3n1  n1 1 11      两式相减得 2 S  1  2  2  2  2n1  1  2 9 93  2n1  2  2n2 ， 3 n 3 32 33 3n 3n1 3  1  3n1 3 3n1 1   3   n1 所以S 1 ， n 3n 16. 【答案】(1)π (2)[1,2] (3)见详解 【分析】（1）先根据向量数量积公式求出 f(x)的表达式，再利用三角函数公式化简，最后 根据周期公式求最小正周期； （2）根据三角函数图象的平移规律得到g(x)的表达式，然后结合给定区间求出g(x)的值域.   【详解】（1）已知a(2 3cosx,1)，b (sinx,cos2x)，可得： 11  f(x)ab 2 3cosxsinxcos2x , 对上式进行化简： f(x) 3sin2xcos2x π 再根据辅助角公式进一步化简得： f(x)2sin(2x ) 6 2π 2π 根据正弦函数的周期公式T  可得 f(x)的最小正周期T   π.  2 π （2）将函数 f(x)图象上所有的点向左平移 个单位，根据“左加右减”的原则， 6 π π π π 可得g(x)的表达式为：g(x) f(x )2sin[2(x ) ]2sin(2x ) 6 6 6 6 π π π 7π 已知x[0, ]，则2x[0,π]，那么2x+ [ , ]. 2 6 6 6 π π π π 当2x  ，即x 时，sin(2x )取得最大值1，此时g(x)取得最大值212. 6 2 6 6 π 7π π π 1 1 当2x  ，即x 时，sin(2x )取得最小值 ，此时g(x)取得最小值2( )1. 6 6 2 6 2 2 π 所以，当x[0, ]时，函数g(x)的值域为[1,2]. 2  1 （3）方法一：ysinx先向右平移 个单位，横坐标缩短为原来的 ，纵坐标扩大到原来 6 2 的2倍. 1  方法二：ysinx横坐标缩小为原来的 ，再向右平移 个单位，纵坐标扩大到原来的2倍. 2 12 3 2 2 22 2 17. 【答案】(1)证明见解析 (2) (3)存在，AF  或 ． 3 3 21 【分析】（1）连接AC，交BD于点O，可得OE//PA，由线面平行的判断可证结论； （2）由题意可得V V V ，求解即可. PBDE PBDC EBDC （3）以O为坐标原点，分别以OA，OB所在直线为x，y轴，以过点O且平行于PD的直 线为z轴，建立空间直角坐标系Oxyz．求出平面BDE与平面BDF 的法向量，由向量夹角的 余弦值求解即可. 【详解】（1）如图，连接AC，交BD于点O，则O为AC的中点．连接OE， 因为E是PC的中点，所以OE//PA． 又OE平面BDE，PA平面BDE， 所以PA//平面BDE． （2）由题意可得 12V V V PBDE PBDC EBDC 因为PD平面ABCD，E为PC中点 1 所以三棱锥PBDE与EBDC的高分别为PD和 PD, 2 连接AC交BD于点O，ABCD菱形BDCD2, 1 1 解得 OC 3 ，S  BDOC 2 3 3 BDC 2 2 又因为PD2所以 1 1 1 V  S PD S  PD PBDE 3 BDC 3 BDC 2 1 1 1 1 1 1 3 V  S  PD  3 PD  3 2 ， PBDE 3 BDC 2 3 2 3 2 3 3 综上三棱锥PBDE的体积为 . 3 3 21 (3)存在点F，使得二面角F BDE的正弦值为 ． 14 因为底面ABCD是菱形，PD底面ABCD，AC,BD平面ABCD， 所以ACBD，PD AC，PD  BD， 故以O为坐标原点，分别以OA，OB所在直线为x，y轴，以过点O且平行于PD的直线为 z轴，建立如图所示的空间直角坐标系Oxyz． 则A ( 3,0,0 ) ，B0,1,0，C   3,0,0  ，D0,1,0，P0,1,2，E   3 , 1 ,1  ，    2 2     3 3     故DB0,2,0，EB , ,1，AP  3,1,2 ．    2 2  设  A  F    A  P     3,,2  ， 0,1 ，      则F  3 3,,2 ，BF   3 3,1,2 ．  设平面BDE的法向量为mx ,y ,z ， 1 1 1 13  2y 0  mDB0  1 则   ， 3 3 mEB0  x  y z  0  2 1 2 1 1 3   3 则y 0，令x  3，则z  ，故m 3,0, ． 1 1 1 2  2  设平面BDF的法向量为n x ,y ,z ， 2 2 2  n  D  B  0   2y 2 0 则 n  B  F  0 ，即    3 3  x 2 (1)y 2 2z 2 0    则y 0，令x 2 3得z 33，故n 2 3,0,33 ． 2 2 2 3 21 因为二面角F BDE的正弦值为 ， 14 2 3 21 7 所以二面角F BDE的余弦值的绝对值为 1     ．  14  14 9   6 1   mn 2 7 令 cos m,n      ， m n 2 14  3 2    3   2 3 2 332 2 1 11 化简得63254110，解得 或 ． 3 21 2 2 22 2 因为 AP 2222 2 2 ，所以AF  或 ． 3 21 x2 1  2 18. 【答案】(1)  y2 1 (2)（ⅰ）直线MN过的定点为 ,0.（ⅱ） . 2 2  8 【分析】（1）根据题意，列出关于a,b,c的方程组，求得a2,b2的值，即可求解； 1 （2）（ⅰ）设直线l 为ykx1，直线l 为y x1，联立方程组，分别求得 1 2 2k  2k2 k   1 k  M , 和N , ，得出直线MN的方程，进而得到MN过的定点. 12k2 12k2 12k2 12k2 1  1 1 k （ⅱ）由MN过的定点为P ,0，求得S  OP y y   ，结合基本不等 2  ΔOMN 2 M N 2 12k2 式，即可求解. x2 y2 2  2 【详解】（1）解：因为椭圆  1的离心率e ，且过点  1,   ， a2 b2 2  2  14c 2   a 2 可得 且c2 a2b2，解得a2 2,b2 1，  1 1  1 a2 2b2 x2 所以椭圆的标准方程为  y2 1. 2 （2）（ⅰ）由（1）知，椭圆 x2  y2 1，可得F 1,0， 2 2 设直线l 的方程为ykx1，l 的方程为y 1 x1，且Cx ,y ，Dx ,y ， 1 2 2k 1 1 2 2 x2 联立方程组   2 y2 1 ，整理得  12k2 x24k2x2k220，  ykx1 4k2 2k2 2 所以x x  ，xx  ， 1 2 12k2 1 2 12k2 x x 2k2 k 因为M 为CD的中点，所以x  1 2  ，y kx 1 ， M 2 12k2 M M 12k2  2k2 k   1 k  即M , ，同理可得N , ， 12k2 12k2 12k2 12k2 k 2k  1  2k  1 直线MN的方程为y  x ，即y x ， 12k2 12k2 12k2 12k2 2 1  所以直线MN过的定点为 ,0. 2  1  （ⅱ）由MN过的定点为P ,0， 2  1 1 2k 1 k 1 1 2 S  OP y y       所以 ΔOMN 2 M N 4 12k2 2 12k2 2 1 8 ， 2 k k 1 当且仅当2k  时，即k  2 时，等号成立，所以OMN 的面积最大值为 2 . k 2 8 9 19. 【答案】(1) (2)证明见解析，D f1 f1 f1  2 (3)x3 10 【分析】（1）为奇数即1,3,5，计算P即可； 3 （2）由条件概率分别求得 p ，p ，p ，再结合p 1，得 p ，进而得到生成的函数为 1 2 3 i 0 i0 f x，依次求 fx， fx，计算 f1 f1 f1  2，并根据公式逐步求出 n D iE2 p ，即可得证 i i0 15（3）经分析得到的可能取值为0，1，2，3，分别求得对应的概率得到的分布列，由生 成的函数记为tx，求导得到tx，并利用导数可求得gxtx的极小值. 1 1 2 3 【详解】（1）由生成的函数为 f x  x x3 x5，知 10 5 5 10 1 1 2 3 f x x0 x10x2 x30x4 x5． 10 5 5 10 1 2 3 所以P1 ，P3 ，P5 ， 5 5 10 9 因此，当为奇数时，PAP1P3P5 ． 10 （2） p i1,2,3恰好是取到红球、蓝球、绿球对应的概率， i 1 1 6 2 2 6 4 4 故 p  1 ，p    ， p    ． 1 7 7 2 7 6 7 3 7 6 7 即 p  p  p 1，故 p 0， 1 2 3 0 1 2 4 所以生成的函数为 f x x x2 x3， 7 7 7 1 4 12 4 24 故 fx  x x2， fx  x， 7 7 7 7 7 2 所以 f1 f1 f1  2  28  17    17   26 ， 7 7  7  49 因为E p 2p 3p ， fx p 2p x3p x2， 1 2 3 1 2 3 1 4 12 17 所以E f1，故E f 1    ， 7 7 7 7 1 2 4 17 （或E1 2 3  ） 7 7 7 7 3 因为D iE2 p ， i i0 2 2 2 2  17  17 1  17 2  17 4 26 所以D0  01   2   3    ，  7   7  7  7  7  7  7 49 故D f1 f1 f1  2． （3）的可能取值为0，1，2，3， C1C1 C2 27 C1C1 C2 18 则P0 3 8 3  ，P1 3 5 3  ， C2 55 C2 55 11 11 C1C1 C2 9 1 1 P2 3 2 3  ，P3  ． C2 55 C2 55 11 11 16则的分布列为  0 1 2 3 27 18 9 1 P 55 55 55 55 27 18 9 1 所以tx  x x2 x3， 55 55 55 55 18 18 3 故gxtx  x x2， 55 55 55 18 6 故gx  x ，令gx0，解得x3， 55 55 故x3时，gx单调递减，x3时，gx单调递增， 故x3是gx的极小值点． 17