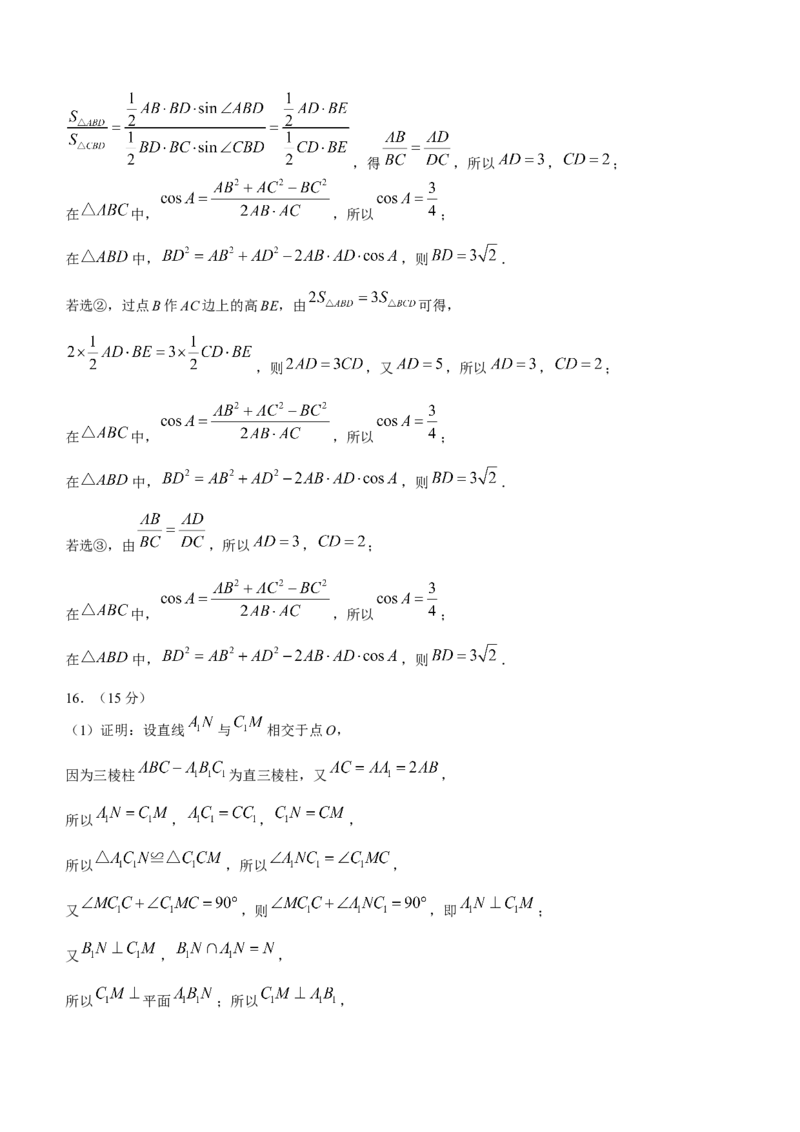文档内容
西山区 2024 届高三第三次教学质量检测
数学试题卷
(本试卷共四个大题19个小题;考试用时120分钟,满分150分)
考生注意:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2,回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,
用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷
上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知复数z满足 ,则 在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.设集合 , ,若 ,则 ( )
A.0 B.1 C.-1 D.
3.记 为等差数列 的前n项和.若 , ,则 ( )
A.10 B.20 C.30 D.40
4.华为云“盘古”气象大模型是世界上首个精度超过传统数值预报方法的AI模型,对比传统方法,预测速
度提高10000倍以上,可秒级完成对全球气象的预测.由“盘古”模型预测,某地某天降雨的概率是0.5,连
续两天降雨的概率是0.3,已知某地某天降雨,则随后一天降雨的概率是( )
A.0.3 B.0.4 C.0.5 D.0.6
5.已知椭圆C: 的左焦点为F,点P在椭圆C上,若 的最大值是最小值的2倍,
则椭圆C的离心率 ( )
A. B. C. D.
6.已知角 的顶点与原点重合,始边与x轴的非负半轴重合,终边与圆 相交于点 ,将
的终边逆时针旋转45°之后与圆 的交点为B,则点B的横坐标为( )
学科网(北京)股份有限公司A. B. C. D.
7.每年6月到9月,昆明大观公园的荷花陆续开放,已知池塘内某种单瓣荷花的花期为3天(第四天完全凋
谢),池塘内共有2000个花蕾,第一天有10个花蕾开花,之后每天花蕾开放的数量都是前一天的2倍,则
在第几天池塘内开放荷花的数量达到最大( )
A.6 B.7 C.8 D.9
8.已知函数 在区间 上单调递增,则a的最小值为( )
A. B. C.e D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知直线a,b,c与平面 , , ,下列说法正确的是( )
A.若 , , ,则a,b异面
B.若 , , ,则
C.若 , ,则
D.若 , ,则
10.直线 与函数 有且仅有三个交点,从左往右依次记作点
A,B,C,则下列说法正确的是( )
A. 的取值范围是 B. 有且仅有2个极大值点
C. 在 上单调递增 D.若 ,则
11.设O为坐标原点,直线l过抛物线C: 的焦点F且与C交于A,B两点(点A在第一象
限), ,l为C的准线, ,垂足为M, ,则下列说法正确的是( )
A. B. 的最小值为
学科网(北京)股份有限公司C.若 ,则 D.x轴上存在一点N,使 为定值
三、填空题:本题共3小题,每小题5分,共计15分.
12.已知向量 , 满足 , ,则 ______.
13.今年哈尔滨冰雪旅游格外火爆,哈尔滨市某公园为欢迎往来游客,设计了一个卡通雪人,雪人放置在上
底边长为3m,下底边长为4m,高为1m的正四棱台冰雕底座上,那么冰雕底座需要______立方米水制成.
(制作过程的损耗忽略不计,冰和水均为理想状态, , )
14.函数 的最小值为______.
四、解答题:本题共5小题,共计77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
记 的内角A,B,C的对边分别为a,b,c.已知 ,且成等差数列, , .
(1)求a,c;
(2)点D在AC上,从下列三个条件中选择一个作为已知,求BD的长.
条件①: ;条件②: ;条件③: .
16.(15分)
直三棱柱 中, ,M为AC的中点,N为 的中点, .
(1)证明: ;
(2)求平面 与平面 所成角的余弦值.
17.(15分)
新高考数学试卷增加了多项选择题,每小题有A、B、C、D四个选项,原则上至少有2个正确选项,至多有
3个正确选项.题目要求:“在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分
选对的得部分分,有选错的得0分.”
其中“部分选对的得部分分”是指:若正确答案有2个选项,则只选1个选项且正确得3分;若正确答案有3
学科网(北京)股份有限公司个选项,则只选1个选项且正确得2分,只选2个选项且都正确得4分.
(1)若某道多选题的正确答案是AB,一考生在解答该题时,完全没有思路,随机选择至少一个选项,至多
三个选项,请写出该生所有选择结果所构成的样本空间,并求该考生得分的概率;
(2)若某道多选题的正确答案是2个选项或是3个选项的概率均等,一考生只能判断出A选项是正确的,其
他选项均不能判断正误,给出以下方案,请你以得分的数学期望作为判断依据,帮该考生选出恰当方案:
方案一:只选择A选项;
方案二:选择A选项的同时,再随机选择一个选项;
方案三:选择A选项的同时,再随机选择两个选项.
18.(17分)
已知双曲线E: 的右焦点为 ,一条渐近线方程为 .
(1)求双曲线E的方程;
(2)是否存在过点 的直线l与双曲线E的左右两支分别交于A,B两点,且使得 ,若存
在,求出直线l的方程;若不存在,说明理由.
19.(17分)
我们把 (其中 , )称为一元n次多项式方程.
代数基本定理:任何复系数一元 次多项式方程(即 , , ,…, 为实数)在复数集内至
少有一个复数根;由此推得,任何复系数一元 次多项式方程在复数集内有且仅有n个复数根(重
根按重数计算).
那么我们由代数基本定理可知:任何复系数一元 次多项式在复数集内一定可以分解因式,转化为
n个一元一次多项式的积.
即 ,其中k, ,
, , ,……, 为方程 的根.
进一步可以推出:在实系数范围内(即 , , ,…, 为实数),方程
的有实数根,则多项式 必可分解因式.例如:
观察可知, 是方程 的一个根,则 一定是多项式 的一个因式,即
,由待定系数法可知, .
学科网(北京)股份有限公司(1)解方程: ;
(2)设 ,其中 , , , ,且 .
(i)分解因式: ;
(ii)记点 是 的图象与直线 在第一象限内离原点最近的交点.求证:当
时, .
西山区 2024 届第三次高三教学质量检测
数学答案
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
题号 1 2 3 4 5 6 7 8
答案 A C C D B B C A
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
题号 9 10 11
答案 AC ACD ABD
三、填空题:本题共3小题,每小题5分,共计15分.
12.2 13.11.1 14.
四、解答题:本题共5小题,共计77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)(书写合理尽量给分)
解:(1)由 ,且成等差数列,则 (Ⅰ)
又 , ,则 ,代入得 (Ⅱ)
联立(Ⅰ)、(Ⅱ)得, ,
(2)若选①,过点B作AC边上的高BE,因为BD平分 ,所以
学科网(北京)股份有限公司,得 ,所以 , ;
在 中, ,所以 ;
在 中, ,则 .
若选②,过点B作AC边上的高BE,由 可得,
,则 ,又 ,所以 , ;
在 中, ,所以 ;
在 中, ,则 .
若选③,由 ,所以 , ;
在 中, ,所以 ;
在 中, ,则 .
16.(15分)
(1)证明:设直线 与 相交于点O,
因为三棱柱 为直三棱柱,又 ,
所以 , , ,
所以 ,所以 ,
又 ,则 ,即 ;
又 , ,
所以 平面 ;所以 ,
学科网(北京)股份有限公司又 , ,
所以 平面 ,则 ,
又 ,所以 .
(注:第一问也可直接建系,按高考评卷标准,有系无论对错既给1分,(1)(2)问不重复给建系分)
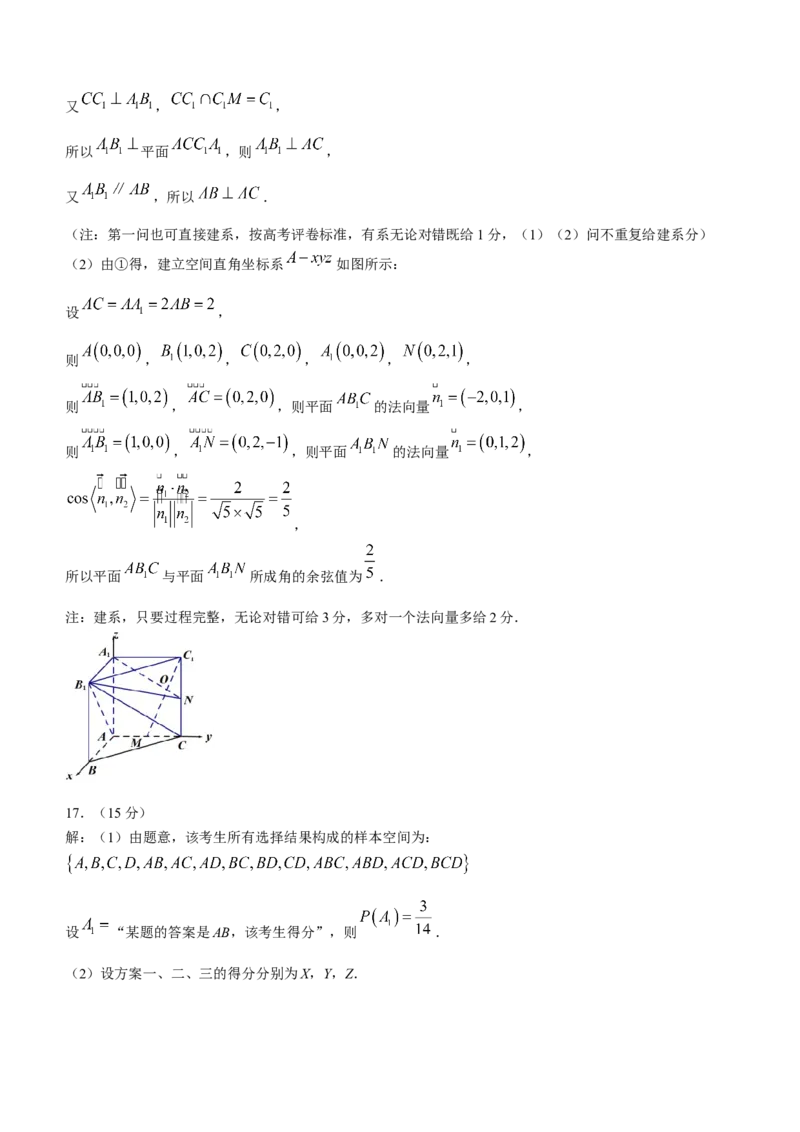
(2)由①得,建立空间直角坐标系 如图所示:
设 ,
则 , , , , ,
则 , ,则平面 的法向量 ,
则 , ,则平面 的法向量 ,
,
所以平面 与平面 所成角的余弦值为 .
注:建系,只要过程完整,无论对错可给3分,多对一个法向量多给2分.
17.(15分)
解:(1)由题意,该考生所有选择结果构成的样本空间为:
设 “某题的答案是AB,该考生得分”,则 .
(2)设方案一、二、三的得分分别为X,Y,Z.
学科网(北京)股份有限公司①∵ , .
∴X的分布列为:
X 2 3
P
则: .
②∵ , , ,
∴Y的分布列为:
Y 0 4 6
P
则: .
③∵ , ,
∴Z的分布列为:
Z 0 6
P
则: .
∵ ,∴以数学期望为依据选择方案一更恰当.
18.(17分)
解:(1)由题知: ,又 , 解得: , ;
则E的方程为 .
(2)设AB中点为 ,由 可知 为等腰三角形, ,
学科网(北京)股份有限公司即 ,可得 , (Ⅰ)
设 , ,则: ,
①-②化简整理得: ,即 ;
可得 (Ⅱ)
联立(Ⅰ)(Ⅱ)解得: ;
所以直线l的方程为: .
(第二问解法多样,几何法,联立方程组都可求解,其他方法参考上面过程合理给分即可)
19.(17分)
解:(1)观察可知: 是方程 的一个根;
所以: ,
由待定系数法可知, , , ;
所以 ,即 或 ,
则方程的根为 , , .
(2)(i)由 可知: 是方程 的一个根;
所以: ,
由待定系数法可知, , , ;
所以
学科网(北京)股份有限公司.
(ii)令 ,即 ,
点 是 的图象与直线 在第一象限内离原点最近的交点,
等价于 是方程 的最小正实根;
由(i)知: 是方程 的一个正实根,
且 ,
设 ,由 , , , 可知 为开口向上的二次函数;
又因为 ,则 一定有一正一负两个实根,设正实根为t;
又 ,可得 ,
所以 ;
当 时, ,
由二次函数单调性可知 ,即 是方程 的最小正实根.
学科网(北京)股份有限公司