文档内容
龙岩一中2024届高三上学期第一次月考
数学试题
(考试时间:120分钟 满分:150分)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.已知集合 ,则 中的元素个数为( )
A.8 B.9 C.10 D.11
2.已知 是定义在 上的函数,则“ 是 上的偶函数”是“
都是 上的偶函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.下列命题中,错误的命题有( )
A.函数 与 不是同一个函数
B.命题“ , ”的否定为“ , ”
C.设函数 ,则 在 上单调递增
D.设 ,则 “ ”是“ ”的必要不充分条件
4.已知函数 ,则使得 成立的 的取值范围是( )
A. B. C. D.
5.某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初时含杂质2%,每过滤
一次可使杂质含量减少1/4,要使产品达到市场要求,则至少应过滤的次数为(已知:
lg2=0.3010,lg3=0.4771)( )
A.8 B.9 C.10 D.11
6.设定义在R上的奇函数 在(0, )上单调递增,且 ,则不等式
的解集为( )
A. B.
C. D.
7.已知 , , ,则( )
A. B.
C. D.
8.定义在 上的函数 满足 , 时 ,若
的解集为 ,其中 ,则实数 的取值范围为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
A⊂B
9.已知 为实数集 的非空集合,则 ¿ 的必要不充分条件可以是( )
学科网(北京)股份有限公司A. B.A∩C B= C.C B C A D.B∪C A=R
R R R R
10.已知 ,下列命题为真命题的是( )
A.若 ,则 B.若 ,则ac2>bc2
C.若 ,则 D.若 ,则
11.已知 是定义在 上的函数,且满足 为偶函数, 为奇函数,则下列
说法正确的是( )
A.函数 的周期为2 B.函数 的周期为4
C.函数 关于点 中心对称 D.
12.函数 和 有相同的最大值 ,直线 与两曲线 和
恰好有三个交点,从左到右三个交点横坐标依次为 ,则下列说法正确的是( )
A. B. C. D.
三、填空题:本题共4小题,每小题5分,共20分.
13.已知实数集R,集合A={x|log x<1},B={x∈Z|x2+4≤5x},则(C A)∩B=
2 R
14.已知正实数a,b满足 ,则 的最小值为 .
15. 已知 则 ______;若函数 的值域为 ,则 的
最小值为______.
16.已知函数 ,若 ,且 ,
则 的值为 .
三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤.
17.(本题满分10分)已知集合 , .
(1)若 =1,求(C B)∩A;
R
(2)若 >0,设命题 ,命题 ,已知命题p是命题q的充分不必要条件,求实数
的取值围.
学科网(北京)股份有限公司18. (本题满分12分)已知函数 是奇函数.
(1)求 ;
(2)若 ,求 的范围.
19.(本题满分12分)
已知函数 , ,且 在区间 上为增函数.
(1)求实数 的取值范围;
(2)若函数 与 的图象有三个不同的交点,求实数 的取值范围.
20. (本题满分12分)
某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产
业结构,调整出 名员工从事第三产业,调整后他们平均每人每年创造利润为
万元 ,剩下的员工平均每人每年创造的利润可以提高 .
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整
出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要
求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a的取值范围是多
少?
学科网(北京)股份有限公司21. (本题满分12分)
已知函数 是 上的奇函数, .
(1)若函数 与 有相同的零点,求 的值;
(2)若 , ,求 的取值范围.
22. (本题满分12分)
已知函数 , .
(1)讨论函数 单调性;
(2)当 时,若函数 在 有两个不同零点,求实数m的取值范围.
学科网(北京)股份有限公司龙岩一中2024届高三上学期第一次月考数学参考答案
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B B C D D D A B ABD CD BCD ABD
13.{2,3,4} 14. 15.2, -3 16.-1
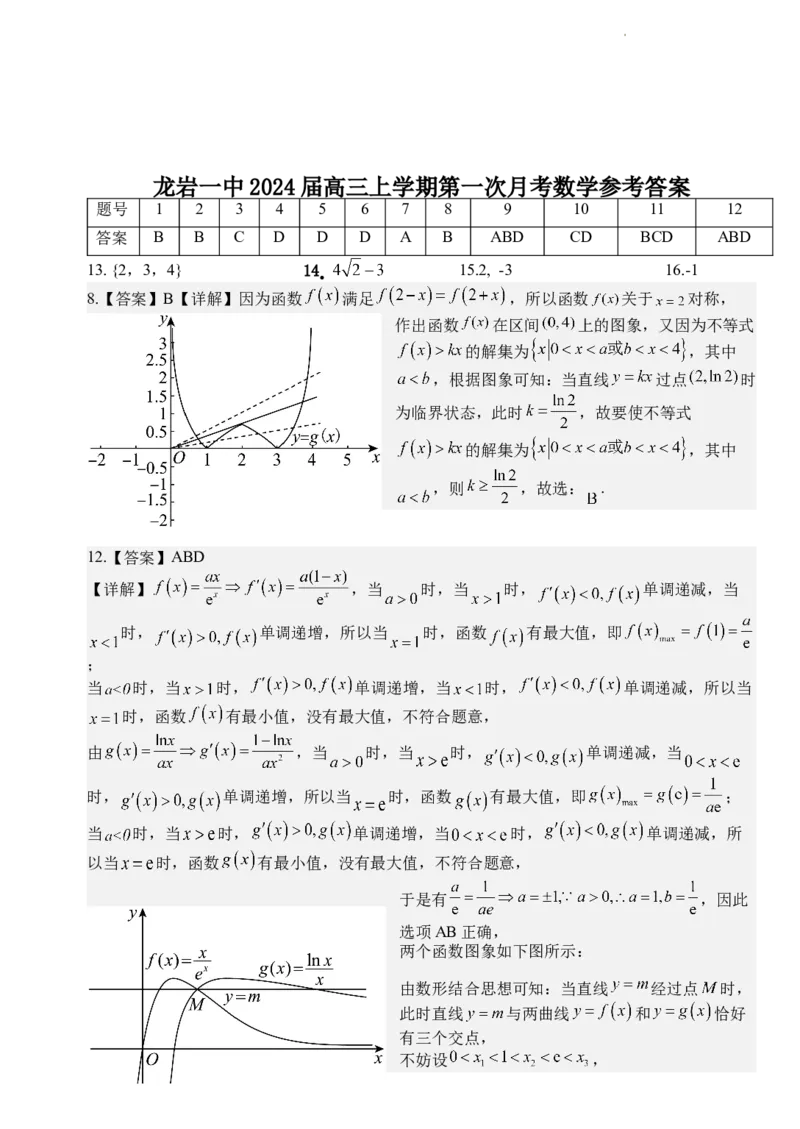
8.【答案】B【详解】因为函数 满足 ,所以函数 关于 对称,
作出函数 在区间 上的图象,又因为不等式
的解集为 ,其中
,根据图象可知:当直线 过点 时
为临界状态,此时 ,故要使不等式
的解集为 ,其中
,则 ,故选: .
12.【答案】ABD
【详解】 ,当 时,当 时, 单调递减,当
时, 单调递增,所以当 时,函数 有最大值,即
;
当 时,当 时, 单调递增,当 时, 单调递减,所以当
时,函数 有最小值,没有最大值,不符合题意,
由 ,当 时,当 时, 单调递减,当
时, 单调递增,所以当 时,函数 有最大值,即 ;
当 时,当 时, 单调递增,当 时, 单调递减,所
以当 时,函数 有最小值,没有最大值,不符合题意,
于是有 ,因此
选项AB正确,
两个函数图象如下图所示:
由数形结合思想可知:当直线 经过点 时,
此时直线 与两曲线 和 恰好
有三个交点,
不妨设 ,
学科网(北京)股份有限公司且 ,
由 ,又 ,又当 时, 单调递增,
所以 ,
又 ,又 ,
又当 时, 单调递减,所以 ,
, ,于是有 ,所以选项D正确,
故选:ABD【点睛】关键点睛:利用数形结合思想,结合等式 是解题的关键.
16.解:作出函数 的图象如下:
令 ,则 ,
由题意,结合图象可得, , ,
所以 , , ,因此 .故答案为: .
17.解:(1)当 时, ,可得 ,
又由 ,所以 . . ........5分
(2)当 时,可得 .因为命题 是命题 的充分不必要条件,则 ,可得
,等号不能同时成立,解得 ,所以实数 的取值范围为 ......10分
18. .......1分
.....................6分 (用特殊值没检验的,扣2分)
. ...............8分
.....................12分
19.解:(1)由题意 ∵ 在区间 上为增函数,
≥0在区间(2,+∞)上恒成立..........2分
即k+1≤x恒成立,又 ,∴ ,故
∴ 的取值范围为 ..........4分 ( 没有等号扣2分)
(2)设 ,
学科网(北京)股份有限公司...........6分
令 得 或 由(1)知 ,
① 当 时, , 在R上递增,显然不合题意...........7
分
②当 时, , 随 的变化情况如下表:
—
↗ ↘ ↗
极小值
极大值
由于 ,欲使 与 的图象有三个不同的交点,即方程 有三个不同的实
根,故需 ,即 ...........10分
∴ ,解得 综上,所求 的取值范围为 ...........12分
,
20. 解:(1)由题意,得 ,..................3分
即 ,又 ,所以 .即最多调整500名员工从事第三产业. ..........5分
(2)从事第三产业的员工创造的年总利润为 万元,
从事原来产业的员工的年总利润为 万元,..............7分
21. 解:(1)因为 是 上的奇函数,所以 ,
即 解得 ..................2分
因为 是函数 的零点,所以 ,则 ....................4分
(2)由(1)可得 ,
,............6分
因为奇函数 ,所以 在 上是减函数,
学科网(北京)股份有限公司则 在 上的最大值为 .......8分
因为 ,所以 在 上是增函数,在 上是减函数.
则 的最小值为 和 中的较小的一个.
因为 , .所以
.............10分
因为 , ,所以 .
解得 .故 的取值范围为 .....................12分
22. 解(1):因为 定义域为 ,
所以 ,..........1分
当 时,令 ,解得 或 ,令 ,解得 ,
所以 在 上单调递减,在 和 上单调递增,..........2分
当 时 恒成立,所以 在 上单调递增, ..........3分
当 时,令 ,解得 或 ,令 ,解得 ,
所以 在 上单调递减,在 和 上单调递增,..........4分
综上可得,当 时, 在 上单调递减,在 和 上单调递增;
当 时, 在 上单调递增;
当 时, 在 上单调递减,在 和 上单调递增;..........5分
解(2):当 时, ,
所以 ,令 ,则 ,
所以 在 上单调递增,所以 ,
①当 ,即 时 ,所以 在 上单调递增,又 ,
所以函数 只有一个零点,不符合题意,舍去;..........6分
②当 ,即 时 ,又 ,
所以存在唯一的 ,使得 ,当 时, ,当 时,
所以 在 上单调递减,在 上单调递增,又 ,
当 时 ,此时 ,所以 ,函数 只有一个零点,不符合题意,舍去;
当 时 , ,此时有两个零点时,应满足 ,..........8分
即 ,
学科网(北京)股份有限公司其中
,..........9分
设 , ,
则 ,令 ,解得 ,
所以当 时 ,当 时 ,
所以 在 上单调递增,在 上单调递减,所以 ,..........11分
即 恒成立,所以 且 ...........12分
【方法点睛】导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常
化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明
常转化为函数的单调性、极(最)值问题处理.
龙岩一中2024届高三上学期第一次月考
数学试题
(考试时间:120分钟 满分:150分)
命题人:王珍连 审题人:马洪亮
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.已知集合 ,则 中的元素个数为( )
A.8 B.9 C.10 D.11
【答案】B【详解】解不等式 得: ,即 ,而
,由 解得: ,又 ,显然满足
的自然数有9个,所以 中的元素个数为9. 故选:B
2.已知 是定义在 上的函数,则“ 是 上的偶函数”是“
都是 上的偶函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】B 【详解】由 都是R上的偶函数,得 ,设
, , 为偶函数,即
“ 都是R上的偶函数时,则 必为偶函数”,反之,“若 为偶函
数,则不一定能推出 都是R上的偶函数”,例如:取
,则 是R上的偶函数,而 都不
具备奇偶性,故“ 是R上的偶函数 ”是“ 都是R上的偶函数” 的必
要不充分条件. 故选:B.
3.下列命题中,错误的命题有( )
A.函数 与 不是同一个函数
学科网(北京)股份有限公司B.命题“ , ”的否定为“ , ”
C.设函数 ,则 在 上单调递增
D.设 ,则 “ ”是“ ”的必要不充分条件
【答案】C 【详解】对于A选项,因为两个函数的定义域不同,所以两个函数是不同的函数,
故A正确;对于B选项,因为存在量词命题的否定是全称量词命题,所以B正确;
对于C选项,因为 ,但是 ,与增函数定义矛盾,所以C错误;
对于D选项,若 ,当 时,推不出 ,当 时, 且 ,
所以D正确. 故选:C.
4.已知函数 ,则使得 成立的 的取值范围是( )
A. B. C. D.
【答案】D【详解】当 时 为增函数,故 时有 成立
所以 ;
当 时 ,故 时有 成立,所以
综上所述:
故选:D
5.某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初时含杂质2%,每过滤
一次可使杂质含量减少1/4,要使产品达到市场要求,则至少应过滤的次数为(已知:
lg2=0.3010,lg3=0.4771)( )
A.8 B.9 C.10 D.11
【答案】D【详解】设至少需要过滤 次,则 ,即 ,
所以 ,即 ,又 ,所以 ,
所以至少过滤11次才能使产品达到市场要求,故选D.
【点睛】本题主要考查指数与对数的运算,考查学生的阅读能力,考查学生的建模能力,属于
中档题.与实际应用相结合的题型也是高考命题的动向,这类问题的特点是通过现实生活的事
例考查书本知识,解决这类问题的关键是耐心读题、仔细理解题,只有吃透题意,才能将实际
问题转化为数学模型进行解
6.设定义在R上的奇函数 在(0, )上单调递增,且 ,则不等式
的解集为( )
A. B.
C. D.
【答案】D【详解】解:由于奇函数 在 上是增函数,则该函数在 上也是增
函数,且 , , ,由 可得
,即 .当 时,得 ,解得 ;
当 时,可得 ,解得 .因此,原不等式的解集为 或
. 故选:D.
学科网(北京)股份有限公司7.已知 , , ,则( )
A. B.
C. D.
【答案】A 【详解】解: , ,
令 ,则 ,当 时, ,当 时, ,
所以函数 在 上递减,在 上递增,令 ,则 ,
当 时, ,当 时, ,所以函数 在 上递减,在 上递
增,所以 ,即 ,所以 ,
即 ,所以 ,由 ,得 ,
由 ,得 , ,因为 ,
所以 ,所以 ,所以 ,即 ,所以 ,
综上所述 .故选:A.
【点睛】本题考查了比较大小的问题,考查了同构的思想,考查了利用导数求函数的单调区间,
解决本题的关键在于构造函数,有一定的难度.
8.定义在 上的函数 满足 , 时 ,若
的解集为 ,其中 ,则实数 的取值范围为( )
A. B. C. D.
【答案】B【详解】因为函数 满足 ,所以函数 关于 对称,
作出函数 在区间 上的图象,又因为不等式
的解集为 ,其中
,根据图象可知:当直线 过点 时
为临界状态,此时 ,故要使不等式
的解集为 ,其中
,则 ,故选: .
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
A⊂B
9.已知 为实数集 的非空集合,则 的必要不充分条件可以是( )
¿
A. B.A∩C B= C.C B C A D.B∪C A=R
R R R R
【答案】ABD
10.已知 ,下列命题为真命题的是( )
学科网(北京)股份有限公司A.若 ,则 B.若 ,则ac2>bc2
C.若 ,则 D.若 ,则
【答案】CD
【分析】由不等式的性质可判断ABC,由作差法可判断D.
【详解】对于A,若 ,则 ,A错误;
对于B,若 ,且 时,则 ,B错误;
对于C,若 ,则 ,故 ,则必有 ,C正确;
对于D,若 ,则 ,
所以 ,D正确.
故选:CD
11.已知 是定义在 上的函数,且满足 为偶函数, 为奇函数,则下列
说法正确的是( )
A.函数 的周期为2
B.函数 的周期为4
C.函数 关于点 中心对称
D.
【答案】BCD
【分析】利用函数的奇偶性、对称性与周期性对选项逐一分析即可.
【详解】解:因为 为偶函数,所以 ,
所以 ,则 ,所以函数 关于直线 对称,
因为 为奇函数,所以 ,所以 ,
所以 ,所以函数 关于点 中心对称,故C正确,
由 与 得 ,即 ,
故 ,所以函数 的周期为4,故 不正确,B正确;
,故D正确.
故选:BCD.
12.函数 和 有相同的最大值 ,直线 与两曲线 和
恰好有三个交点,从左到右三个交点横坐标依次为 ,则下列说法正确的是( )
A. B. C. D.
【答案】ABD【详解】 ,当 时,当 时,
单调递减,当 时, 单调递增,所以当 时,函数 有最大值,即
;当 时,当 时, 单调递增,当 时,
单调递减,所以当 时,函数 有最小值,没有最大值,不符合题意,
学科网(北京)股份有限公司由 ,
当 时,当 时, 单调递减,当 时, 单调递增,所
以当 时,函数 有最大值,即 ;
当 时,当 时, 单调递增,当 时, 单调递减,所
以当 时,函数 有最小值,没有最大值,不符合题意,
于是有 ,因此选项AB正确,
两个函数图象如下图所示:
由数形结合思想可知:当直线 经过点 时,
此时直线 与两曲线 和 恰好
有三个交点,
不妨设 ,
且 ,
由 ,又
,又当 时, 单调递增,所以 ,又
,又 ,又当 时, 单调递减,
所以 , , ,于是有 ,所以选项D正
确,
故选:ABD
【点睛】关键点睛:利用数形结合思想,结合等式 是解题的关键.
三、填空题:本题共4小题,每小题5分,共20分.
13.已知实数集R,集合A={x|log x<1},B={x∈Z|x2+4≤5x},则(C A)∩B=
2 R
【答案】{2,3,4}
解析 由log x<1,解得00,设命题 ,命题 ,已知命题p是命题q的充分不必要条件,求实数
的取值围.
17解:(1)当 时, ,可得 ,
又由 ,所以 . . ........5分
(2)当 时,可得 .因为命题 是命题 的充分不必要条件,则 ,可得
, 等 号 不 能 同 时 成 立 , 解 得 , 所 以 实 数 的 取 值 范 围 为
......10分
18. (本题满分12分)已知函数 是奇函数.
(1)求 ;
(2)若 ,求 的范围.
.......1分
.....................6分 (用特殊值没检验的,扣2分)
学科网(北京)股份有限公司.....................8分
.....................12分
19.(本题满分12分)
已知函数 , ,且 在区间 上为增函数.
(1)求实数 的取值范围;
(2)若函数 与 的图象有三个不同的交点,求实数 的取值范围.
解:(1)由题意 ∵ 在区间 上为增函数,
≥0在区间(2,+∞)上恒成立..........2分
即k+1≤x恒成立,又 ,∴ ,故
∴ 的取值范围为 ..........4分 ( 没有等号扣2分)
(2)设 ,
...........6分
令 得 或 由(1)知 ,
② 当 时, , 在R上递增,显然不合题意...........7
分
②当 时, , 随 的变化情况如下表:
—
↗ ↘ ↗
极小值
极大值
由于 ,欲使 与 的图象有三个不同的交点,即方程 有三个不同的实
根,故需 ,即 ...........10分
,解得
∴ ,
综上,所求 的取值范围为 ...........12分
20. (本题满分12分)
某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产
业结构,调整出 名员工从事第三产业,调整后他们平均每人每年创造利润为
学科网(北京)股份有限公司万元 ,剩下的员工平均每人每年创造的利润可以提高 .
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整
出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要
求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a的取值范围是多
少?
解:(1)由题意,得 ,..................3分
即 ,又 ,所以 .即最多调整500名员工从事第三产业. ..........5分
(2)从事第三产业的员工创造的年总利润为 万元,
从事原来产业的员工的年总利润为 万元,..............7分
21. (本题满分12分)
已知函数 是 上的奇函数, .
(1)若函数 与 有相同的零点,求 的值;
(2)若 , ,求 的取值范围.
解:(1)因为 是 上的奇函数,所以 ,
即 解得 ..................2分
因为 是函数 的零点,所以 ,
则 ....................4分
(2)由(1)可得 ,
学科网(北京)股份有限公司,............6分
因为奇函数 ,所以 在 上是减函数,
则 在 上的最大值为 .......8分
因为 ,所以 在 上是增函数,在 上是减函数.
则 的最小值为 和 中的较小的一个.
因为 , .所以
.............10分
因为 , ,所以 .
解得 .故 的取值范围为 .....................12分
22. (本题满分12分)
已知函数 , .
(1)讨论函数 单调性;
(2)当 时,若函数 在 有两个不同零点,求实数m的取值范围.
解(1):因为 定义域为 ,
所以 ,..........1分
当 时,令 ,解得 或 ,令 ,解得 ,
所以 在 上单调递减,在 和 上单调递增,..........2分
当 时 恒成立,所以 在 上单调递增, ..........3分
当 时,令 ,解得 或 ,令 ,解得 ,
所以 在 上单调递减,在 和 上单调递增,..........4分
综上可得,当 时, 在 上单调递减,在 和 上单调递增;
当 时, 在 上单调递增;
当 时, 在 上单调递减,在 和 上单调递增;..........5分
解(2):当 时, ,
学科网(北京)股份有限公司所以 ,令 ,则 ,
所以 在 上单调递增,所以 ,
①当 ,即 时 ,所以 在 上单调递增,又 ,
所以函数 只有一个零点,不符合题意,舍去;..........6分
②当 ,即 时 ,又 ,
所以存在唯一的 ,使得 ,当 时, ,当 时,
所以 在 上单调递减,在 上单调递增,又 ,
当 时 ,此时 ,所以 ,函数 只有一个零点,不符合题意,舍去;
当 时 , ,此时有两个零点时,应满足 ,..........8分
即 ,
其中
,..........9分
设 , ,
则 ,令 ,解得 ,
所以当 时 ,当 时 ,
所以 在 上单调递增,在 上单调递减,所以 ,..........11分
即 恒成立,
所以 且 ...........12分
【方法点睛】导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常
化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明
常转化为函数的单调性、极(最)值问题处理.
学科网(北京)股份有限公司