文档内容
绝密★启用前
2024-2025 学年度上学期
广东省三校“决胜高考,梦圆乙巳”
第一次联合模拟考试
物理
参加学校:诺德安达学校、金石实验中学、英广实验学校
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,请2B用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮
擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
一、单选题:本大题共7小题,共28分。
1
. 分 如图所示,质量为m的物体在一个与水平方向成 角的拉力F作用下,沿水平面向右匀速运动,已
知重(4力加) 速度大小为g,下列关于物体在时间t内所受力的𝜃𝜃冲量正确的是
( )
A. 拉力F的冲量大小为Ft B. 拉力F的冲量大小为
C. 摩擦力的冲量大小为Ft D. 重力的冲量大小为0 𝐹𝐹𝐹𝐹cos𝜃𝜃
2
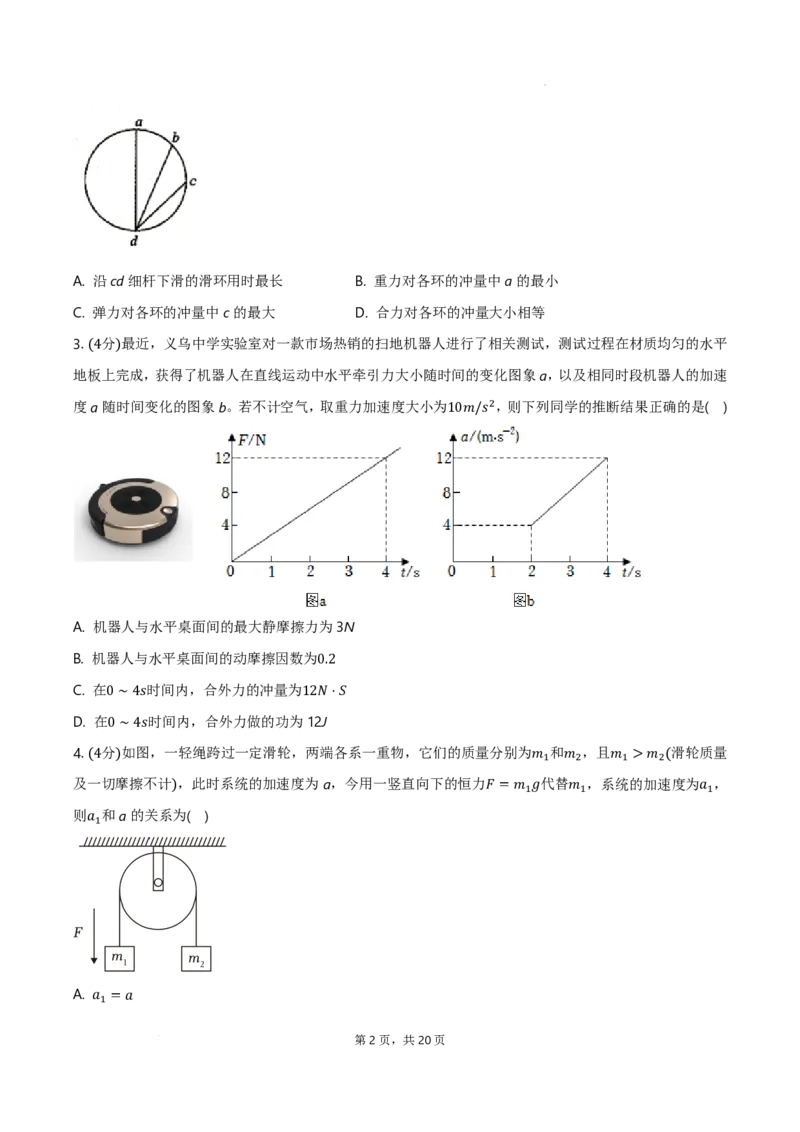
. 分 如图所示,ad、bd、cd 是竖直面内三根固定的光滑细杆,a、b、c、d 位于同一圆周上,a 点为圆
周的(4最)高点,d点为最低点。每根杆上都套着一个完全相同的小滑环 图中未画出 ,三个滑环分别从a、b、
c点无初速释放,下列关于它们下滑到d过程的说法中正确的是 ( ) ( )
第1页,共20页
学科网(北京)股份有限公司A. 沿cd细杆下滑的滑环用时最长 B. 重力对各环的冲量中a的最小
C. 弹力对各环的冲量中c的最大 D. 合力对各环的冲量大小相等
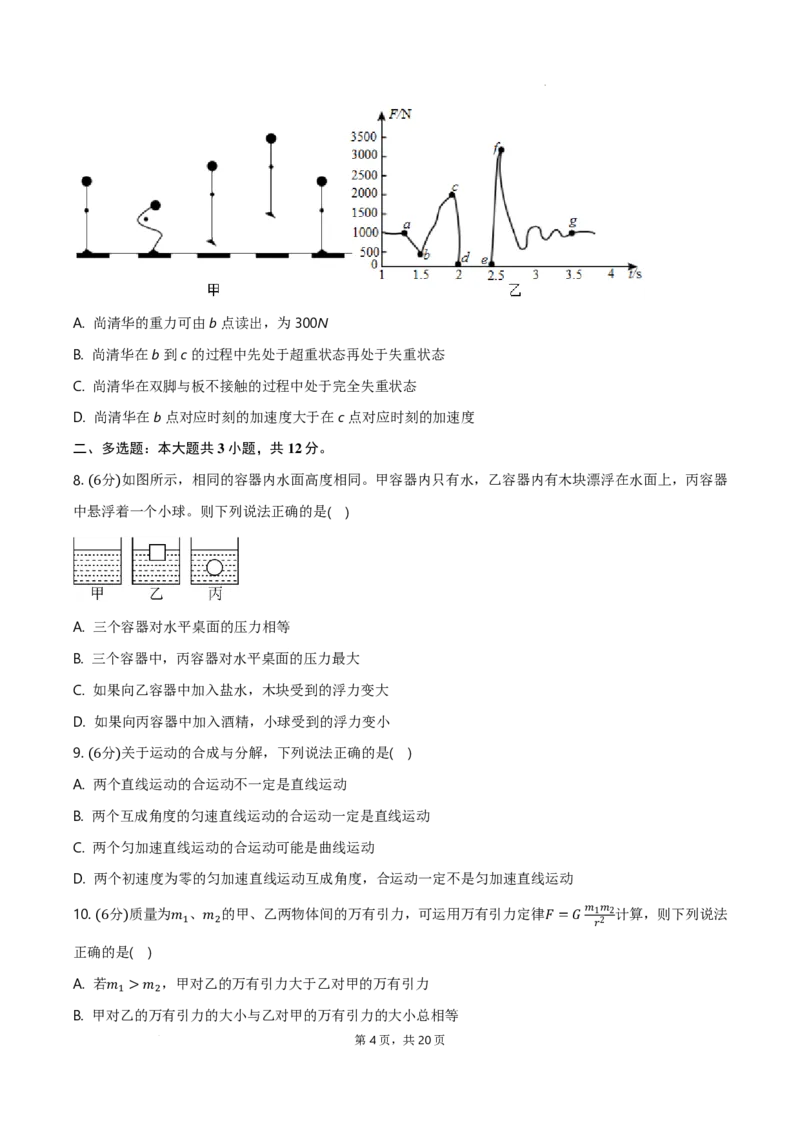
. 分 最近,义乌中学实验室对一款市场热销的扫地机器人进行了相关测试,测试过程在材质均匀的水平
3
地板(4上完) 成,获得了机器人在直线运动中水平牵引力大小随时间的变化图象a,以及相同时段机器人的加速
度a随时间变化的图象b。若不计空气,取重力加速度大小为 ,则下列同学的推断结果正确的是
( )
2
10𝑚𝑚/𝑠𝑠
A. 机器人与水平桌面间的最大静摩擦力为3N
B. 机器人与水平桌面间的动摩擦因数为
C. 在 时间内,合外力的冲量为 0.2
D. 在0∼4𝑠𝑠时间内,合外力做的功为1122𝑁𝑁J ⋅𝑆𝑆
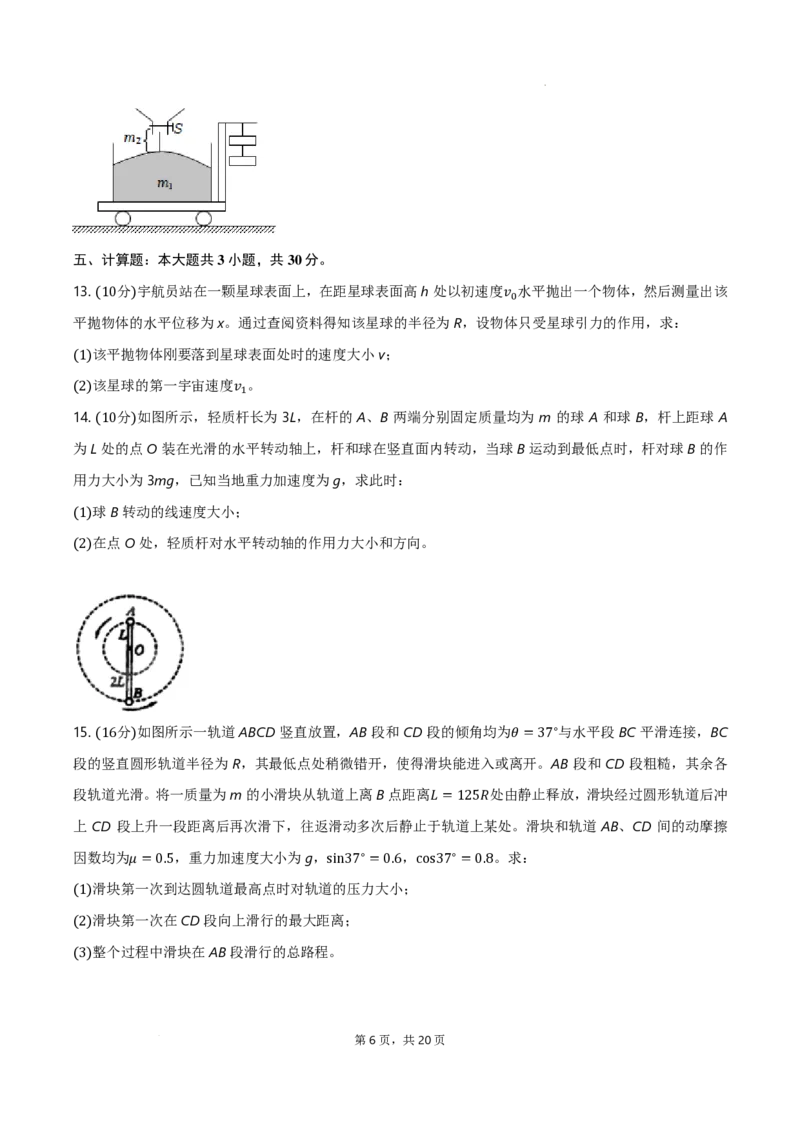
4
. 分0∼如4图𝑠𝑠,一轻绳跨过一定滑轮,两端各系一重物,它们的质量分别为 和 ,且 滑轮质量
及一(4切摩) 擦不计 ,此时系统的加速度为 a,今用一竖直向下的恒力 𝑚𝑚代1 替𝑚𝑚2 ,系𝑚𝑚统1的>加𝑚𝑚速2(度为 ,
则 和a的关系)为 ( ) 𝐹𝐹 =𝑚𝑚1𝑔𝑔 𝑚𝑚1 𝑎𝑎1
𝑎𝑎1
A.
𝑎𝑎1 =𝑎𝑎
第2页,共20页
学科网(北京)股份有限公司B.
𝑚𝑚1+𝑚𝑚2
𝑎𝑎1 = 𝑚𝑚2 𝑎𝑎
C.
𝑚𝑚1
𝑎𝑎1 =𝑚𝑚2𝑎𝑎
D.
𝑚𝑚2
5 .
𝑎𝑎1
分
= 如𝑚𝑚图1𝑎𝑎
所示,将 a、b 两小球以不同的初速度同时水平抛出,它们均落在水平地面上的 P 点,a 球抛
出时(4的高) 度比b球的高.P点到两球起抛点的水平距离相等,不计空气阻力,与b球相比,a球
( )
A. 初速度较大
B. 速度变化率较大
C. 落地时速度方向与其初速度方向的夹角较小
D. 落地时速度方向与其初速度方向的夹角较大
. 分 图为一辆某建设工地上运送沙石的厢式自卸车,到达目的地后准备卸下车厢内的沙子,此时车头朝
6
前,(4车厢) 在液压顶作用下缓慢抬高,车厢与水平面的夹角 逐渐增大,整个卸沙过程汽车车轮相对地面始终
静止。对此下列说法正确的是 ( ) 𝛼𝛼
A. 车厢内的沙子没有滑动时,随着夹角 逐渐增大,汽车受到沙子的作用力越来越大
B. 车厢内的沙子没有滑动时,随着夹角𝛼𝛼逐渐增大,汽车受到地面的支持力越来越大
C. 当夹角 为某一值时,沙子恰好匀速下𝛼𝛼滑,汽车受到地面的摩擦力为零
D. 当夹角𝛼𝛼为某一值时,沙子恰好匀速下滑,汽车受到地面的静摩擦力方向向前
7
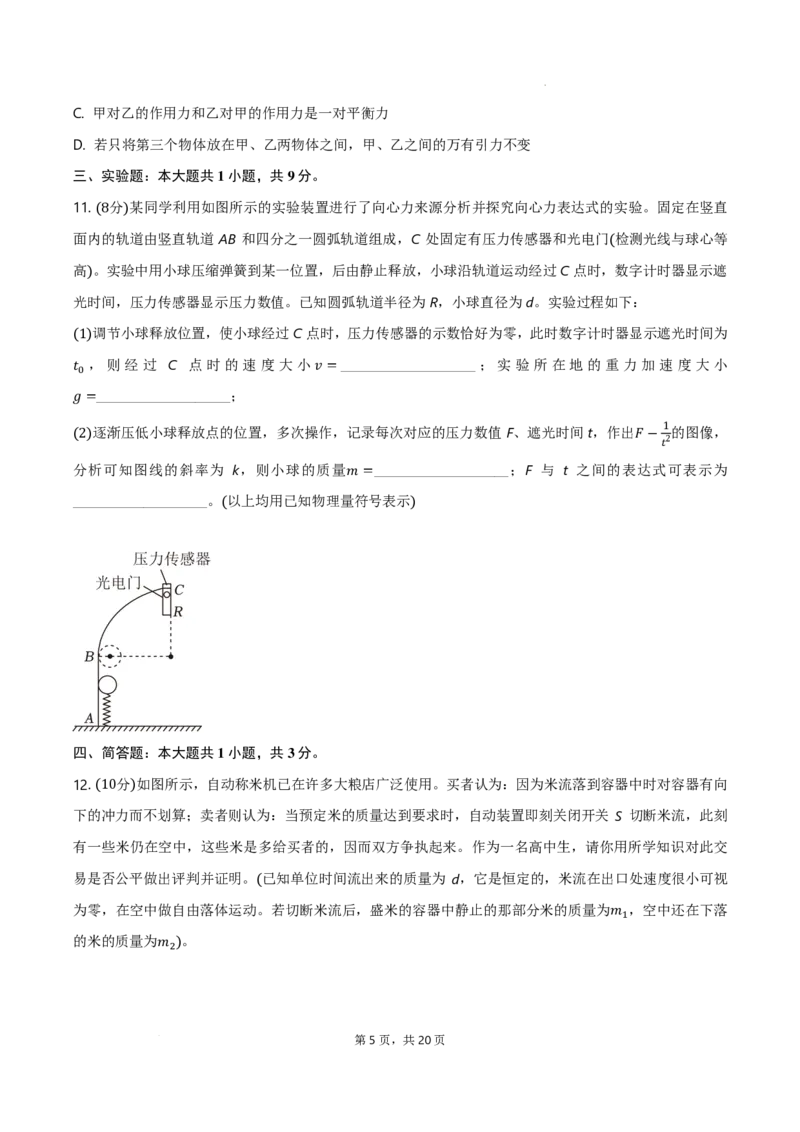
. 分 图甲𝛼𝛼 是莱芜一中尚清华同学站在接有力传感器的板上做下蹲、起跳动作的示意图,图中的O点表示
他的(4重心) 。图乙是传感器所受压力随时间变化的图像,图像上 a、b 两点的纵坐标分别为 900N 和 300N,
重力加速度 ,不计空气阻力。根据图像分析可知
( )
2
𝑔𝑔 =10𝑚𝑚/𝑠𝑠 第3页,共20页
学科网(北京)股份有限公司A. 尚清华的重力可由b点读出,为300N
B. 尚清华在b到c的过程中先处于超重状态再处于失重状态
C. 尚清华在双脚与板不接触的过程中处于完全失重状态
D. 尚清华在b点对应时刻的加速度大于在c点对应时刻的加速度
二、多选题:本大题共3小题,共12分。
. 分 如图所示,相同的容器内水面高度相同。甲容器内只有水,乙容器内有木块漂浮在水面上,丙容器
8
中悬(6浮着) 一个小球。则下列说法正确的是
( )
A. 三个容器对水平桌面的压力相等
B. 三个容器中,丙容器对水平桌面的压力最大
C. 如果向乙容器中加入盐水,木块受到的浮力变大
D. 如果向丙容器中加入酒精,小球受到的浮力变小
9. 分 关于运动的合成与分解,下列说法正确的是( )
A. (两6 个)直线运动的合运动不一定是直线运动
B. 两个互成角度的匀速直线运动的合运动一定是直线运动
C. 两个匀加速直线运动的合运动可能是曲线运动
D. 两个初速度为零的匀加速直线运动互成角度,合运动一定不是匀加速直线运动
10. 分 质量为 、 的甲、乙两物体间的万有引力,可运用万有引力定律 计算,则下列说法
𝑚𝑚1𝑚𝑚2
正确 (6 的是 ) ( ) 𝑚𝑚1 𝑚𝑚2 𝐹𝐹 =𝐺𝐺 𝑟𝑟 2
A. 若 ,甲对乙的万有引力大于乙对甲的万有引力
B.
甲对𝑚𝑚1乙>的𝑚𝑚万2有引力的大小与乙对甲的万有引力的大小总相等
第4页,共20页
学科网(北京)股份有限公司C. 甲对乙的作用力和乙对甲的作用力是一对平衡力
D. 若只将第三个物体放在甲、乙两物体之间,甲、乙之间的万有引力不变
三、实验题:本大题共1小题,共9分。
11. 分 某同学利用如图所示的实验装置进行了向心力来源分析并探究向心力表达式的实验。固定在竖直
面内(的8 轨)道由竖直轨道 AB 和四分之一圆弧轨道组成,C 处固定有压力传感器和光电门 检测光线与球心等
高 。实验中用小球压缩弹簧到某一位置,后由静止释放,小球沿轨道运动经过C点时,(数字计时器显示遮
光)时间,压力传感器显示压力数值。已知圆弧轨道半径为R,小球直径为d。实验过程如下:
调节小球释放位置,使小球经过C点时,压力传感器的示数恰好为零,此时数字计时器显示遮光时间为
(1),则经过 C 点时的速度大小 ___________________;实验所在地的重力加速度大小
𝐹𝐹0 ___________________; 𝑣𝑣 =
𝑔𝑔 =逐渐压低小球释放点的位置,多次操作,记录每次对应的压力数值 F、遮光时间 t,作出 的图像,
1
(2) 𝐹𝐹− 2
分析可知图线的斜率为 k,则小球的质量 ___________________;F 与 t 之间的表达式𝐹𝐹可表示为
___________________。 以上均用已知物理量𝑚𝑚符=号表示
( )
四、简答题:本大题共1小题,共3分。
. 分 如图所示,自动称米机已在许多大粮店广泛使用。买者认为:因为米流落到容器中时对容器有向
12
下的(1冲0力而) 不划算;卖者则认为:当预定米的质量达到要求时,自动装置即刻关闭开关 S 切断米流,此刻
有一些米仍在空中,这些米是多给买者的,因而双方争执起来。作为一名高中生,请你用所学知识对此交
易是否公平做出评判并证明。 已知单位时间流出来的质量为 d,它是恒定的,米流在出口处速度很小可视
为零,在空中做自由落体运动(。若切断米流后,盛米的容器中静止的那部分米的质量为 ,空中还在下落
的米的质量为 。 𝑚𝑚1
𝑚𝑚2)
第5页,共20页
学科网(北京)股份有限公司五、计算题:本大题共3小题,共30分。
13. 分 宇航员站在一颗星球表面上,在距星球表面高h处以初速度 水平抛出一个物体,然后测量出该
平抛(1物0体的) 水平位移为x。通过查阅资料得知该星球的半径为R,设物𝑣𝑣体0只受星球引力的作用,求:
该平抛物体刚要落到星球表面处时的速度大小v;
(1)该星球的第一宇宙速度 。
(124). 分 如图所示,轻质𝑣𝑣杆1长为 3L,在杆的 A、B 两端分别固定质量均为 m 的球 A 和球 B,杆上距球 A
为L(处10的点) O装在光滑的水平转动轴上,杆和球在竖直面内转动,当球B运动到最低点时,杆对球B的作
用力大小为3mg,已知当地重力加速度为g,求此时:
球B转动的线速度大小;
(1)在点O处,轻质杆对水平转动轴的作用力大小和方向。
( 2)
15. 分 如图所示一轨道ABCD 竖直放置,AB段和CD 段的倾角均为 与水平段BC 平滑连接,BC
∘
段的(1竖6直圆) 形轨道半径为R,其最低点处稍微错开,使得滑块能进入或离𝜃𝜃开=。37AB 段和CD 段粗糙,其余各
段轨道光滑。将一质量为m的小滑块从轨道上离B点距离 处由静止释放,滑块经过圆形轨道后冲
上 CD 段上升一段距离后再次滑下,往返滑动多次后静止于𝐿𝐿轨=道12上5𝑅𝑅某处。滑块和轨道 AB、CD 间的动摩擦
因数均为 ,重力加速度大小为g, , 。求:
∘ ∘
滑块第𝜇𝜇一=次0到.5达圆轨道最高点时对轨道s的in3压7力=大0小.6;c os37 =0.8
(1)滑块第一次在CD段向上滑行的最大距离;
(2)整个过程中滑块在AB段滑行的总路程。
( 3)
第6页,共20页
学科网(北京)股份有限公司第7页,共20页
学科网(北京)股份有限公司答案和解析
1.【答案】A
【解析】【考点】动量定理;动量冲量.
【专题】定量思想;推理法;动量定理应用专题;推理能力.
【答案】A
【分析】由平衡条件表达摩擦力和支持力,根据冲量的定义式求解各个力的冲量。
【解答】解:AB、根据冲量的定义式可知拉力F的冲量大小为Ft,故A正确,B错误;
C、根据平衡条件可得摩擦力 ,根据冲量的定义式可知摩擦力的冲量大小为 ,故C错误。
D、根据平衡条件可得支持力 𝑓𝑓 =𝐹𝐹cos𝜃𝜃 ,根据冲量的定义式可知支持力N的冲量大𝐹𝐹𝐹𝐹小co为s𝜃𝜃 ,
故D错误; 𝑁𝑁 =𝑚𝑚𝑔𝑔−𝐹𝐹sin𝜃𝜃 (𝑚𝑚𝑔𝑔−𝐹𝐹sin𝜃𝜃)𝐹𝐹
故选:A。
【点评】本题主要是考查冲量的计算和动量定理,知道一个力的冲量就等于该力乘以作用时间,合外力的
冲量等于动量的变化。
2.【答案】C
【解析】【考点】动量定理.
【专题】比较思想;推理法;动量定理应用专题;推理能力.
【答案】C
【分析】计算出滑环沿杆下滑的加速度,根据几何关系得到各细杆的长度,然后根据运动学公式得到下滑
的时间;重力的冲量等于重力与时间的乘积;弹力的冲量等于弹力与时间的乘积;合力的冲量等于各个分
力冲量的矢量和。
【解答】解:A、设光滑细杆与水平方向的夹角为 ,细杆的长度为 ,其中R表示圆周的半径,根
据牛顿第二定律可知滑环沿细杆下滑的加速度大小𝛼𝛼为 ,则𝐿𝐿滑=环𝑅𝑅沿sin细𝛼𝛼杆下滑到d的时间为t,则
𝑎𝑎 =𝑔𝑔sin𝛼𝛼 𝐿𝐿 =
,得 可以看出滑环沿细杆下滑到d的时间是一个与夹角 无关的量。即它们
1 2 2𝐿𝐿 2𝑅𝑅sin𝛼𝛼 2𝑅𝑅
下2𝑎𝑎滑𝐹𝐹 到d 𝐹𝐹的=时�间 𝑎𝑎相=等�, 故𝑔𝑔sinA𝛼𝛼错=误�; 𝑔𝑔 . 𝛼𝛼
B、重力的冲量 ,滑环完全相同,所以质量相等,由上面的分析可知时间也相等,所以重力对各环
的冲量相等,故𝐼𝐼𝐺𝐺B=错𝑚𝑚误𝑔𝑔;𝐹𝐹
C、各环所受弹力为 ,所以弹力对各环的冲量大小为 ,其中 c 杆与水平方向的
𝑁𝑁 =𝑚𝑚𝑔𝑔cos𝛼𝛼 𝐼𝐼𝑁𝑁 =𝑚𝑚𝑔𝑔cos𝛼𝛼⋅𝐹𝐹
第8页,共20页
学科网(北京)股份有限公司夹角最小,即c杆对环的弹力最大,时间都是相等的,故弹力对各环的冲量中c的最大,故C正确;
D、根据动能定理可以知道a环下滑到底端时的速度最大,由上面的分析知道这个是等时圆模型,所以它们
下滑到底端所用时间是相等的,根据动量定理可以知道合力的冲量等于物体动量的变化量,所以合力对 a
环的冲量最大,故D错误。
故选:C。
【点评】这是一个等时圆模型,可以快速的得到滑环沿细杆下滑的时间相等,然后根据冲量的定义即可比
较冲量的大小。
3.【答案】A
【解析】【考点】动量定理;牛顿第二定律;功的计算.
【专题】定量思想;推理法;动量定理应用专题;推理能力.
【答案】A
【分析】由图像求解时间,及摩擦力,由牛顿第二定律求解动摩擦因数,由冲量公式求解 C 选项,由动能
定理求解合外力做功。
【解答】解: 由图b可知加速度的表达式为
𝐴𝐴.
3−1
𝑎𝑎则=可得 (𝐹𝐹−𝐹𝐹0)=𝐹𝐹−𝐹𝐹0
4−2
𝐹𝐹即0 =1s1时𝑠𝑠 加速度为零,则最大静摩擦力为
12
𝑓𝑓故 𝑚𝑚 A=正确×;1 𝑁𝑁 =3𝑁𝑁
4
B.2s时的牵引力为
12
𝐹𝐹由 2 =a、图×b2结𝑁𝑁合=牛6𝑁𝑁顿第二定律可得
4
𝐹𝐹4−𝑓𝑓 =𝑚𝑚𝑎𝑎4
𝐹𝐹联2立−可𝑓𝑓 =得机𝑚𝑚𝑎𝑎器2人质量
𝑚𝑚滑动=摩3𝑘𝑘擦𝑔𝑔力为
第9页,共20页
学科网(北京)股份有限公司𝑓𝑓机=器3人𝑁𝑁与水平桌面间的动摩擦因数为
𝑓𝑓 𝑓𝑓
𝜇𝜇解=得
𝐹𝐹𝑁𝑁
=
𝑚𝑚 𝑔𝑔
故B𝜇𝜇错=误0;.1
C.在 时间内,合外力的冲量为
0−4𝑠𝑠
0+3
𝐼𝐼故=C𝑚𝑚错𝑎𝑎𝐹𝐹误=;3 × ×(4−1)𝑁𝑁⋅𝑠𝑠 =13.5𝑁𝑁⋅𝑠𝑠
2
D.4s末机器人的速度为
3
𝑣𝑣在=𝑎𝑎𝐹𝐹 =时间×内3𝑚𝑚,/合𝑠𝑠 =外4力.5做𝑚𝑚的/𝑠𝑠功为
2
0−4𝑠𝑠
代入数据,解得
1 2
𝑊𝑊故D =错2𝑚𝑚误𝑣𝑣
.
𝑊𝑊 =30.375𝐽𝐽
故选:A。
【点评】本题考查动量定理,学生除熟练掌握公式运用,还需灵活数形结合,综合求解。
4.【答案】B
【解析】【考点】牛顿运动定律的应用——连接体模型;力的合成与分解的应用;牛顿第二定律.
【专题】定量思想;整体法和隔离法;牛顿运动定律综合专题;分析综合能力.
【答案】B
【分析】定滑轮两端各系一重物时,对整体,根据牛顿第二定律求出加速度 a 与两个物体质量的关系。当
用一竖直向下的恒力 代替 时,对 ,根据牛顿第二定律求出 ,最后求 和a的关系。
【解答】解:定滑轮两𝐹𝐹端=各𝑚𝑚系1𝑔𝑔一重物𝑚𝑚1时,对整𝑚𝑚体2,根据牛顿第二定律得:𝑎𝑎1 𝑎𝑎1 ,得
; (𝑚𝑚1−𝑚𝑚2)𝑔𝑔 =(𝑚𝑚1+𝑚𝑚2)𝑎𝑎 𝑎𝑎 =
𝑚𝑚1−𝑚𝑚2
𝑚𝑚当1用+𝑚𝑚一2𝑔𝑔
竖直向下的恒力 代替 时,对 ,根据牛顿第二定律得: ,得
,则 𝐹𝐹 =,故𝑚𝑚1 A 𝑔𝑔 CD错𝑚𝑚误 1 ,B正确𝑚𝑚2 。 𝑚𝑚1𝑔𝑔−𝑚𝑚2𝑔𝑔=𝑚𝑚2𝑎𝑎1 𝑎𝑎1 =
𝑚𝑚1−𝑚𝑚2 𝑚𝑚1+𝑚𝑚2
故𝑚𝑚选2: 𝑔𝑔 B。 𝑎𝑎1 = 𝑚𝑚2 𝑎𝑎
【点评】本题是连接体问题,要灵活选择研究对象,运用牛顿第二定律列式解答,要注意整体法和隔离法
第10页,共20页
学科网(北京)股份有限公司的应用。
5.【答案】D
【解析】【考点】平抛运动.
【专题】定性思想;方程法;平抛运动专题.
【答案】D
【分析】平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动,运动时间由下落的高
度决定,根据水平位移与时间结合可分析初速度关系,速度变化率等于重力加速度,由速度的合成求落地
时速度大小和方向.
【解答】解:A、两个小球都做平抛运动,竖直方向做自由落体运动,由 ,得 ,则 。
1 2 2ℎ
小球水平方向都做匀速直线运动,由 ,由题意x相等,又 ℎ,=则2知𝑔𝑔𝐹𝐹 𝐹𝐹 =故� A 𝑔𝑔错误。𝐹𝐹𝑎𝑎 >𝐹𝐹𝑏𝑏
B、根据 ,则知速度变化率𝑥𝑥相=同𝑣𝑣, 0𝐹𝐹故B错误。 𝐹𝐹𝑎𝑎 >𝐹𝐹𝑏𝑏 𝑣𝑣𝑎𝑎 <𝑣𝑣𝑏𝑏.
𝛥𝛥𝑣𝑣
𝛥𝛥𝐹𝐹 =𝑎𝑎 =𝑔𝑔
C、D、落地时速度 ,落地时速度方向与其初速度方向的夹角正切
2 2 2 𝑣𝑣𝑦𝑦
𝑣𝑣 =� 𝑣𝑣0 +𝑣𝑣𝑦𝑦 =� 𝑣𝑣0 +2𝑔𝑔ℎ tan𝛼𝛼 =𝑣𝑣0 =
,则知a的h大, 小, 大,落地时速度方向与其初速度方向的夹角大,故C错误,D正确。
� 2𝑔𝑔ℎ
故𝑣𝑣选0 :D。 𝑣𝑣0 tan𝛼𝛼
【点评】平抛运动常用的研究方法是运动的分解法,只要掌握两个分运动的规律,通过合成即可知道平抛
运动的规律.
6.【答案】C
【解析】【考点】一般情况下的共点力平衡;力的合成与分解的应用.
【专题】定性思想;推理法;共点力作用下物体平衡专题;推理能力.
【答案】C
【分析】根据平衡条件,分析沙子受到的作用力,再根据牛顿第三定律,分析汽车受到沙子的作用力;
根据平衡条件,分析汽车受到地面的支持力;
沙子恰好匀速下滑,处于平衡状态,此时汽车受到地面的摩擦力为零。
【解答】解: 当车厢内的沙子没有滑动时,沙子受到重力和汽车给的作用力,沙子受到汽车的作用力和重
力是平衡力,𝐴𝐴根. 据平衡条件,二者大小相等,方向相反,则沙子受到的作用力不变,由牛顿第三定律可知
随着夹角 逐渐增大,汽车受到沙子的作用力不变,故A错误;
B.当车厢内𝛼𝛼的沙子没有滑动时,汽车和沙子整体受到重力和地面的支持力,是一对平衡力,根据平衡条件,
二者大小相等,方向相反,重力不变,则支持力不变,所以随着夹角 逐渐增大,汽车受到地面的支持力不
第11页,共20页 𝛼𝛼
学科网(北京)股份有限公司变,故B错误;
当夹角为某一值时,沙子恰好匀速下滑,汽车和沙子整体受到重力和地面的支持力,处于平衡状态,此
𝐶𝐶时𝐶𝐶汽. 车受到地面的摩擦力为零,故C正确,D错误;
故选:C。
【点评】本题考查学生对平衡条件的掌握,处于平衡状态的物体受力特点为,若受到两个力作用,则二者
大小相等,方向相反。
7.【答案】C
【解析】【考点】牛顿运动定律的应用——超重和失重.
【专题】应用题;定性思想;推理法;牛顿运动定律综合专题;理解能力;推理能力;分析综合能力.
【答案】C
【分析】人处于平衡状态时,可以读出重力;
弹力小于重力是失重,弹力大于重力是超重;
只受重力作用时是完全失重状态;
根据牛顿第二定律可求加速度大小;
【解答】解:A、开始时人处于平衡状态,人对传感器的压力为900N,人的重力也是900N,故A错误;
B、从b到c的过程中,人对板的压力先小于人的真实重力,后大于人的真实重力,则人先处于失重状态而
后是超重状态,故B错误;
C、离开板后,人只受重力的作用,处于完全失重的状态,故C正确;
D、b点对应时刻的弹力与重力的差值要小于c点对应时刻的弹力与重力的差值,则人在b点对应时刻的加
速度要小于c点对应时刻的加速度,故D错误;
故选:C。
【点评】明确超重和失重的概念,知道完全失重状态的受力情况是解决问题的关键。
8.【答案】AD
【解析】【考点】弹力的产生、方向.
【专题】定性思想;推理法;受力分析方法专题;分析综合能力.
【答案】AD
【分析】 三个相同的容器内水面高度相同,根据 可知其对容器底的压强,再利用 比较三
个容器对水(1平) 桌面的压力; 𝑝𝑝=𝜌𝜌𝑔𝑔ℎ 𝐹𝐹 =𝑝𝑝𝑆𝑆
第12页,共20页
学科网(北京)股份有限公司物体漂浮或悬浮,受到的浮力都等于物体重。
(2)当物体的密度大于液体的密度时,物体下沉;当物体的密度小于液体的密度时,物体上浮 漂浮 ;当物
体(3)的密度等于液体的密度时,物体处于悬浮状态。 ( )
【解答】解:AB、因水平面受到的压力等于物体的总重力,
则甲容器对桌面的压力 ﹣﹣﹣﹣﹣﹣﹣﹣﹣①
甲 水 杯
𝐹𝐹 =𝐺𝐺 +𝐺𝐺
乙容器对桌面的压力 ;
乙 水 木 杯
′
𝐹𝐹 =𝐺𝐺 +𝐺𝐺 +𝐺𝐺
因为木块漂浮,所以
浮 木 排
𝐹𝐹 =𝐺𝐺 =𝐺𝐺
则乙容器对桌面的压力 ﹣﹣﹣﹣﹣﹣﹣﹣﹣②
乙 水 排 杯
′
𝐹𝐹 =𝐺𝐺 +𝐺𝐺 +𝐺𝐺
甲、乙两容器的底面积相同且水的深度相同,则 ﹣﹣﹣﹣﹣﹣﹣﹣﹣③
水 水 排
′
𝐺𝐺 =𝐺𝐺 +𝐺𝐺
所以由①23 可知,甲容器对桌面的压力等于乙容器对桌面的压力;同理可知,甲容器对桌面的压力等于丙
容器对桌面的压力;故A正确,B错误;
C、木块漂浮在水面上,若向乙容器中加入盐水,液体的密度增大,木块仍然漂浮在液面上,则木块受到的
浮力等于木块的重力,木块的重力没变,所以木块受到的浮力不变;故C错误。
D、小球悬浮在丙容器中,所以 如果向丙容器中加入酒精,则液体密度减小,而 不变,由
球 水 排 浮
𝜌𝜌 =𝜌𝜌 𝑉𝑉 𝐹𝐹 =
可知,小球受到的浮力变小,则小球将下沉,故D正确。
浮 排
𝜌𝜌 𝑔𝑔𝑉𝑉
故选:AD。
【点评】本题考查了学生对液体压强公式、物体浮沉条件的掌握和运用,本题关键:一是知道物体密度小
于液体密度时物体漂浮,物体密度等于液体密度时物体悬浮,当物体的密度大于液体的密度时,物体下沉;
二是影响液体压强的因素是液体密度和液体深度。
9.【答案】ABC
【解析】【考点】运动的合成与分解.
【专题】定性思想;合成分解法;运动的合成和分解专题;推理能力.
【答案】ABC
【分析】当合速度的方向与合加速度的方向在同一条直线上,合运动是直线运动,不在同一条直线上,合
运动是曲线运动。
【解答】解:A、两个直线运动的合运动不一定是直线运动,例如平抛运动,故A正确;
B、两个匀速直线运动合成,合加速度为零,合运动仍然是匀速直线运动,故B正确;
第13页,共20页
学科网(北京)股份有限公司C、根据曲线运动的条件可知,当两个匀加速直线运动的合初速度的方向与它们的合加速度的方向不在同
一条直线上时,物体做曲线运动,故C正确;
D、两个初速为零的匀加速直线运动互成角度,由于合初速度为0,所以合运动一定是匀加速直线运动,故
D错误;
故选:ABC。
【点评】本题考查运动的合成与分解,解决本题的关键是掌握判断合运动是直线运动还是曲线运动的方法:
看合速度的方向与合加速度的方向。
10.【答案】BD
【解析】【考点】万有引力定律的应用.
【专题】定性思想;推理法;万有引力定律的应用专题;理解能力.
【答案】BD
【分析】万有引力定律的条件是适用于两质点间的万有引力,自然界中任意两个物体都有万有引力,两物
体间相互的万有引力是一对作用力和反作用力.
【解答】解:ABC、甲对乙的万有引力与乙对甲的万有引力是一对作用力和反作用力,所以甲对乙的万有引
力的大小与乙对甲的万有引力的大小总相等,故B正确,AC错误;
D、若只将第三个物体放在甲乙两物体之间,甲乙之间的万有引力不变,故D正确。
故选:BD。
【点评】解决本题的关键知道万有引力定律适用的条件,知道平衡力与作用力、反作用力的区别.
11.【答案】 、 ; 、 。
2
𝑑𝑑 2𝑑𝑑 𝑘𝑘(2𝑅𝑅−𝑑𝑑) 𝑘𝑘 𝑘𝑘
【解析】【考
(1
点
)𝐹𝐹】0
探(2究𝑅𝑅−圆𝑑𝑑)周𝐹𝐹0
2
运
(
动
2)
的相2𝑑𝑑关
2
参数
𝐹𝐹
问
=
题𝐹𝐹
2
;
−
生𝐹𝐹0
2
活中的圆周运动——竖直平面内的圆周运动.
【专题】定量思想;实验分析法;牛顿第二定律在圆周运动中的应用;能力层次;实验能力.
【答案】 、 ; 、 。
2
𝑑𝑑 2𝑑𝑑 𝑘𝑘(2𝑅𝑅−𝑑𝑑) 𝑘𝑘 𝑘𝑘
【分析】 (1) 根𝐹𝐹0据(瞬2𝑅𝑅时−𝑑𝑑速)𝐹𝐹0 2 度的 (2 定 ) 义2求𝑑𝑑 2 小球经 𝐹𝐹 = 过𝐹𝐹C 2− 点𝐹𝐹的0 2 速度,结合此时压力为零,由牛顿第二定律、几何关系
等求重力(加1)速度;
改变小球释放的位置,得到 图像。根据牛顿第二定律等写出 表达式,结合图像的斜率的值,
1 1
(2) 𝐹𝐹− 2 𝐹𝐹− 2
𝐹𝐹 𝐹𝐹
求出小球的质量,并简化 表达式。
1
𝐹𝐹− 2
𝐹𝐹
第14页,共20页
学科网(北京)股份有限公司【解答】解: 已知小球经过光电门的时间为 ,小球的直径d同时是小球经过光电门时的位移,由
𝑥𝑥
(1) 𝐹𝐹0 𝑣𝑣 = 𝐹𝐹
可得,小球经过C点时的速度大小为:
𝑑𝑑
𝑣𝑣 =𝐹𝐹0
根据重力提供向心力有:
2
𝑚𝑚𝑣𝑣
𝑚𝑚𝑔𝑔= 𝑟𝑟
由题分析可知:
𝑑𝑑
𝑟𝑟 =𝑅𝑅−2
将速度值 代入,联立以上三式可得: 。
2
𝑑𝑑 2𝑑𝑑
𝑣𝑣 =𝐹𝐹0 𝑔𝑔 =
(2𝑅𝑅−𝑑𝑑)𝐹𝐹0
2
当小球运动至光电门时,加速度方向竖直向下,重力及压力的合力提供向心力:
向
2
𝑚𝑚𝑣𝑣
( 而 2) 速度: , 𝐹𝐹 = 𝑟𝑟 =𝐹𝐹+𝑚𝑚𝑔𝑔
2
𝑑𝑑 2𝑑𝑑
联立以上 𝑣𝑣 三 = 式 𝐹𝐹 可得 𝑔𝑔 = (2𝑅𝑅的−𝑑𝑑关)𝐹𝐹0 2 系式为:
2 2
1 2𝑚𝑚𝑑𝑑 2𝑚𝑚𝑑𝑑
𝐹𝐹− 2 𝐹𝐹 = 2− 2
𝐹𝐹 (2𝑅𝑅−𝑑𝑑)𝐹𝐹 (2𝑅𝑅−𝑑𝑑)𝐹𝐹0
由题中已知 的图像斜率为k,则:
2
1 2𝑚𝑚𝑑𝑑
变形可得:
𝐹𝐹−
𝐹𝐹
2 𝑘𝑘 =(2𝑅𝑅−𝑑𝑑)
𝑘𝑘(2𝑅𝑅−𝑑𝑑)
𝑚𝑚 = 2
将k值代入以上表达2𝑑𝑑式后得:
𝑘𝑘 𝑘𝑘
𝐹𝐹 = 2− 2
𝐹𝐹 𝐹𝐹0
故答案为: ; ; 。
2
𝑑𝑑 2𝑑𝑑 𝑘𝑘(2𝑅𝑅−𝑑𝑑) 𝑘𝑘 𝑘𝑘
【点评】本 ( 题 1) 考𝐹𝐹0查的(2𝑅𝑅是−学𝑑𝑑)𝐹𝐹生0 2( 对 2) 于圆2𝑑𝑑周 2 运动 𝐹𝐹 相 = 关𝐹𝐹 2 知 − 识𝐹𝐹0 2 及数学关系中各量的运算能力,需要将各物理量,按照
匀速圆周运动的规律,列出数学方程式,经方程式变换的相关物理量。
12.【答案】自动称米机是准确的,不存在哪方划算不划算的问题,为公平交易。
【解析】【考点】动量定理;自由落体运动.
【专题】定量思想;推理法;动量定理应用专题;分析综合能力.
【答案】自动称米机是准确的,不存在哪方划算不划算的问题,为公平交易。
【分析】根据动量定理和牛顿第三定律可知称米机读数包含了静止在容器中的那部分米的质量 ,也包含
了尚在空中的下落的米的质量 ,即自动称米机是准确的。 𝑚𝑚1
【解答】解:设落到已静止的𝑚𝑚米2堆上的一小部分米的质量为 。在极短时间 内,取 为研究对象,这
部分米很少,则有 , 𝛥𝛥𝑚𝑚 𝛥𝛥𝐹𝐹 𝛥𝛥𝑚𝑚
设其落到米堆上之𝛥𝛥前𝑚𝑚的=速𝑑𝑑度𝛥𝛥𝐹𝐹为v,经 时间静止,如图所示,取竖直向上为正方向,
由动量定理得, 𝛥𝛥 𝐹𝐹
(𝐹𝐹−𝛥𝛥𝑚𝑚𝑔𝑔)𝛥𝛥𝐹𝐹 =𝛥𝛥𝑚𝑚𝑣𝑣 第15页,共20页
学科网(北京)股份有限公司即,
因 𝐹𝐹很=小𝑑𝑑,𝑣𝑣故+𝑑𝑑𝛥𝛥𝐹𝐹𝑔𝑔
根𝛥𝛥据𝐹𝐹牛顿第三定𝐹𝐹 =律𝑑𝑑知𝑣𝑣
𝐹𝐹称=米𝐹𝐹机′的读数应为
,
𝑁𝑁 𝑚𝑚1𝑔𝑔+𝐹𝐹′ 𝑣𝑣
𝑀𝑀 = 𝑔𝑔 = 𝑔𝑔 =𝑚𝑚1+𝑑𝑑𝑔𝑔
因切断米流后空中尚有 时间内对应的米流在空中,故
𝑣𝑣
𝑔𝑔
,
𝑣𝑣
𝑑𝑑 可𝑔𝑔见 = , 𝑚𝑚2
即自动称𝑀𝑀米=机𝑚𝑚1是+准𝑚𝑚确2的,不存在哪方划算不划算的问题,为公平交易。
答:自动称米机是准确的,不存在哪方划算不划算的问题,为公平交易。
【点评】本题考查动量定理在生活中的应用,解题过程中应用到了数学知识,有一定难度。
13.【答案】 该平抛物体刚要落到星球表面处时的速度大小为 ;
2 2ℎ𝑣𝑣0 2
该星球的 ( 第 1) 一宇宙速度为 。 � 𝑣𝑣0 +( 𝑥𝑥 )
𝑣𝑣0
( 2) 𝑥𝑥 √ 2ℎ𝑅𝑅
【解析】【考点】万有引力定律的应用;第一、第二和第三宇宙速度;平抛运动;向心力.
【专题】定量思想;方程法;万有引力定律在天体运动中的应用专题;分析综合能力.
【答案】 该平抛物体刚要落到星球表面处时的速度大小为 ;
2 2ℎ𝑣𝑣0 2
该星球 ( 的 1) 第一宇宙速度为 。 � 𝑣𝑣0 +( 𝑥𝑥 )
𝑣𝑣0
( 【 2) 分析】 由平抛运动的规律𝑥𝑥 ,√ 2 可 ℎ𝑅𝑅 得月球表面重力加速度,再根据动能定理求解物体刚要落到星球表面处
时的速度(大1)小;
该星球的第一宇宙速度即为卫星绕该星球表面做圆周运动的线速度,由万有引力提供向心力的速度表达
式(2),可得该星球的第一宇宙速度 。
【解答】解: 该物体在星球表𝑣𝑣面1 做平抛运动,设下落时间为t,该星球表面的重力加速度为g,则有:
水平方向: (1)
𝑥𝑥 =𝑣𝑣0𝐹𝐹
第16页,共20页
学科网(北京)股份有限公司竖直方向:
1 2
ℎ =2𝑔𝑔𝐹𝐹
联立解得:
2
2ℎ𝑣𝑣0
𝑔𝑔 = 𝑥𝑥 2
设物体的质量为m,物体从抛出到落到星球表面过程中,根据动能定理可得:
1 2 1 2
𝑚𝑚𝑔𝑔ℎ =2𝑚𝑚𝑣𝑣 −2𝑚𝑚𝑣𝑣0
解得: ;
2 2ℎ𝑣𝑣0 2
该星𝑣𝑣球=的�第 𝑣𝑣0 一+宇(宙𝑥𝑥速)度即为卫星绕该星球表面做圆周运动的线速度,设卫星的质量为 ,根据卫星的重
(力2)等于向心力可得: 𝑚𝑚′
2
𝑣𝑣1
𝑚𝑚′𝑔𝑔=𝑚𝑚′
该星球的第一宇宙速度 。
𝑅𝑅
𝑣𝑣0
𝑣𝑣1 =� 𝑔𝑔𝑅𝑅 = 𝑥𝑥 √ 2ℎ𝑅𝑅
答: 该平抛物体刚要落到星球表面处时的速度大小为 ;
2 2ℎ𝑣𝑣0 2
该 ( 星 1) 球的第一宇宙速度为 。 � 𝑣𝑣0 +( 𝑥𝑥 )
𝑣𝑣0
( 【 2) 点评】对于在星体表面做平𝑥𝑥抛√ , 2ℎ 或 𝑅𝑅 竖直上抛之类的运动,其目的一般都是让通过给定的运动求得星球表
面的重力加速度,再根据万有引力与重力的关系、万有引力提供向心力等知识进行解答。
14.【答案】 球B转动的线速度大小为 ;
在点O处(,1)轻质杆对水平转动轴的作用2�力 𝑔𝑔大𝐿𝐿小为3mg,方向竖直向下。
( 2)
【解析】【考点】生活中的圆周运动——竖直平面内的圆周运动;牛顿第二定律;牛顿第三定律;向心力.
【专题】计算题;定量思想;推理法;圆周运动中的临界问题;牛顿第二定律在圆周运动中的应用;分析
综合能力.
【答案】 球B转动的线速度大小为 ;
在点O(1处),轻质杆对水平转动轴的2作�用 𝑔𝑔𝐿𝐿力大小为3mg,方向竖直向下。
(【2)分析】 小球B受重力和弹力的合力提供向心力,根据牛顿第二定律列式求解球B转动的线速度大小;
球的(角1)速度等于B 球的角速度,对A 球运用牛顿第二定律列式求解;杆受力平衡,先根据牛顿第三定
(律2)求𝐴𝐴解两个球对杆的作用力,再结合平衡条件求解转轴对杆的作用力,最后结合牛顿第三定律求解轻质杆
对水平转动轴的作用力大小和方向。
【解答】解: 小球B受重力和弹力的合力提供向心力,根据牛顿第二定律:
2
𝑣𝑣𝐵𝐵
其中: (1) 𝐹𝐹𝐵𝐵−𝑚𝑚𝑔𝑔=𝑚𝑚2𝐿𝐿
𝐹𝐹𝐵𝐵 =3𝑚𝑚𝑔𝑔
第17页,共20页
学科网(北京)股份有限公司联立解得球B转动的线速度大小为:
球的角速度等于B球的角速度,𝑣𝑣根 𝐵𝐵 据=2� 𝑔𝑔𝐿𝐿,可知此时A球的速度为:
1
(对2)
A
𝐴𝐴球受力分析,根据牛顿第二定律得:𝑣𝑣 =𝑅𝑅𝑅𝑅 𝑣𝑣𝐴𝐴 =2𝑣𝑣𝐵𝐵
2
𝑣𝑣𝐴𝐴
𝐹𝐹联𝐴𝐴立+解𝑚𝑚𝑔𝑔得=:𝑚𝑚
𝐿𝐿
根据牛顿第𝐹𝐹三𝐴𝐴定=律0可知球A对杆得作用力为零,球B对杆有竖直向下的拉力,为:
轻杆受力平衡,故水平转动轴对轻杆的作用力向上,为: 𝐹𝐹𝐵𝐵′=3𝑚𝑚𝑔𝑔
根据牛顿第三定律可得轻质杆对水平转动轴的作用力大小𝑁𝑁为:=𝐹𝐹𝐵𝐵′=3𝑚𝑚𝑔𝑔 ,方向竖直向下
答: 球B转动的线速度大小为 ; 𝑁𝑁′=𝑁𝑁 =3𝑚𝑚𝑔𝑔
在(点1)O处,轻质杆对水平转动2轴�的 𝑔𝑔𝐿𝐿作用力大小为3mg,方向竖直向下。
(【2)点评】本题关键是明确小球的向心力来源,然后根据牛顿第二定律、牛顿第三定律、平衡条件列式求解。
15.【答案】 滑块第一次到达圆轨道最高点时对轨道的压力大小为45mg;
滑块第一(次1)在CD段向上滑行的最大距离为25R;
(2)整个过程中滑块在AB段滑行的总路程 。
( 3) 137.5𝑅𝑅
【解析】【考点】功能关系;生活中的圆周运动——竖直平面内的圆周运动;动能定理.
【专题】定量思想;推理法;牛顿第二定律在圆周运动中的应用;动能定理的应用专题;功能关系能量守
恒定律;分析综合能力.
【答案】 滑块第一次到达圆轨道最高点时对轨道的压力大小为45mg;
滑块第(一1)次在CD段向上滑行的最大距离为25R;
(2)整个过程中滑块在AB段滑行的总路程 。
(【3)分析】 滑块从静止释放到第一次到达1圆37轨.5道𝑅𝑅最高点过程利用动能定理列式,在圆轨道最高点由牛顿第
二定律列(式1),联立方程可得支持力大小,由牛顿第三定律可得压力大小;
滑块从静止释放到第一次在CD段速度减为零过程利用动能定理求解;
(2)根据滑块在圆轨道最高点的临界速度利用动能定理可得滑块在 CD 段滑行的距离与第二问中的结果相比
较(3),可知滑块能再次滑行到AB段,根据第二问中的滑块在两斜面上滑行距离的关系可得滑块第二次向上在
AB段滑行的距离,利用动能定理可得滑块第三次通过B点速度大小,根据B点速度大小利用动能定理可知
滑块速度减为零时运动的位置和滑块在AB段运动的总路程。
【解答】解: 滑块从静止释放到第一次到达圆轨道最高点过程,由动能定理有:
(1)
第18页,共20页
𝑚𝑚𝑔𝑔𝐿𝐿sin𝜃𝜃−𝜇𝜇𝑚𝑚𝑔𝑔𝐿𝐿cos𝜃𝜃−
学科网(北京)股份有限公司1 2
2𝑚𝑚𝑔𝑔𝑅𝑅 =2𝑚𝑚𝑣𝑣
在圆轨道最高点由牛顿第二定律有:
2
𝑚𝑚𝑣𝑣
代入数据可得: 𝐹𝐹𝑁𝑁+𝑚𝑚𝑔𝑔 = 𝑅𝑅
由牛顿第三定律可𝐹𝐹𝑁𝑁知=滑45块𝑚𝑚对𝑔𝑔轨道的压力大小 与支持力 大小相等,即:
设滑块第一次在 CD 段向上滑行的最大距𝐹𝐹离𝑁𝑁′为 ,滑块𝐹𝐹𝑁𝑁从静止释放到第一𝐹𝐹𝑁𝑁次′=在𝐹𝐹𝑁𝑁CD=段45速𝑚𝑚度𝑔𝑔 减为零过程,
(由2)动能定理有: 𝐿𝐿1
代入数据可得:𝑚𝑚𝑔𝑔𝐿𝐿sin𝜃𝜃 −𝜇𝜇𝑚𝑚𝑔𝑔𝐿𝐿cos𝜃𝜃−𝑚𝑚𝑔𝑔𝐿𝐿1sin𝜃𝜃−𝜇𝜇𝑚𝑚𝑔𝑔𝐿𝐿1cos𝜃𝜃 =0
𝐿𝐿1 =25𝑅𝑅
根据上面分析可知:
𝐿𝐿1 25𝑅𝑅 1
(3) 𝐿𝐿 =125𝑅𝑅=5
滑块恰好通过圆轨道最高点时,由牛顿第二定律有:
2
𝑚𝑚𝑣𝑣0
设滑块在CD轨道上向下滑行的距离为 时,滑块恰好𝑚𝑚通𝑔𝑔过=圆𝑅𝑅轨道最高点时,滑块从CD段静止滑下到恰好
通过圆轨道最高点过程,由动能定理有𝐿𝐿: 0
1 2
代入数据可得:
𝑚𝑚𝑔𝑔𝐿𝐿0sin𝜃𝜃−𝜇𝜇𝑚𝑚𝑔𝑔𝐿𝐿0cos𝜃𝜃−2𝑚𝑚𝑔𝑔𝑅𝑅 =2𝑚𝑚𝑣𝑣0
,可知滑𝐿𝐿块0第=一12次.5从𝑅𝑅 CD轨道滑下后能再次在AB轨道滑行,同理可知滑块第一次在AB轨道向上滑
𝐿𝐿行 0 的<最𝐿𝐿1 大距离满足:
1 1
设滑块第三次通过 B 𝐿𝐿2 点=的5𝐿𝐿速 1 =度5为×25,𝑅𝑅 =滑5块𝑅𝑅从 AB 轨道第二次滑下过程,由动能定理有:
𝑣𝑣𝐵𝐵3 𝑚𝑚𝑔𝑔𝐿𝐿2sin𝜃𝜃−
1 2
𝜇𝜇代𝑚𝑚入𝑔𝑔𝐿𝐿数 2 据cos可𝜃𝜃得=:2𝑚𝑚𝑣𝑣𝐵𝐵3
设滑块以 𝑣𝑣𝐵𝐵3 =上� 升2𝑔𝑔到𝑅𝑅圆轨道的高度为h,由动能定理有: ,可得 ,可知滑
1 2
块速度减𝑣𝑣为 𝐵𝐵 零 3 =,�反 2向𝑔𝑔𝑅𝑅运动滑到AB段,滑块不能再次滑到CD轨道−上𝑚𝑚,𝑔𝑔ℎ =0−2𝑚𝑚𝑣𝑣𝐵𝐵3 ℎ =𝑅𝑅
滑块第三次通过B点到速度减为零的过程,由动能定理有:
1 2
代入数据可得: −𝜇𝜇𝑚𝑚𝑔𝑔cos𝜃𝜃⋅𝑠𝑠 =0−2𝑚𝑚𝑣𝑣𝐵𝐵3
整个过程中滑块在𝑠𝑠 =
A
2
B
.5段𝑅𝑅滑行的总路程:
总
𝑠𝑠 =𝐿𝐿+2𝐿𝐿2+𝑠𝑠 =125𝑅𝑅+2×5𝑅𝑅+2.5𝑅𝑅 =137.5𝑅𝑅
答: 滑块第一次到达圆轨道最高点时对轨道的压力大小为45mg;
滑(块1)第一次在CD段向上滑行的最大距离为25R;
(2)整个过程中滑块在AB段滑行的总路程 。
(【3)点评】本题考查了动能定理、牛顿第二定1律37,.5解𝑅𝑅 题的关键是利用动能定理判断滑块从CD段再次滑下时能
第19页,共20页
学科网(北京)股份有限公司否上升到圆轨道的最高点,从AB段再次滑下时上升到圆轨道的哪个位置,从而判断滑块下一步的运动特点。
第20页,共20页
学科网(北京)股份有限公司