贵阳第一中学2024届高考适应性月考卷（二）数学-答案(1)_2023年10月_0210月合集_2024届贵州省贵阳市第一中学高三上学期高考适应性月考（二）

贵阳第一中学 2024 届高考适应性月考卷（二） 数学参考答案 一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只 有一项是符合题目要求的） 题号 1 2 3 4 5 6 7 8 答案 A C D B C A A B 【解析】 1 ． 因 为 A{x|x2 5x40}{x|x4或x1} ， B{x|x30}{x|x3} ， 所 以 AB{x|x1}，故选A． 1 2 5  1 1  1 1 2．因为x0，所以x 0，所以yx  x  3≥2 x   2 2x1 2  2 1  2 1 x x 2 2 1 1 1 31，当且仅当x  ，即x 时等号成立，所以函数的最小值为1，故选C． 2 1 2 x 2 3．(2ax)(1x)5的展开式中x2的系数为25，即2C2 aC1 25，解得a1．设(2x)(1x)5 5 5 a axa x2 a x3 a x4 a x5 a x6，令x1，得325 a a a a a a 0 1 2 3 4 5 6 0 1 2 3 4 5 a ，令x1，得0a a a a a a a ，两式相加得，a a a a 3 6 0 1 2 3 4 5 6 0 2 4 6 24 48，故选D． 3x1 1 3x1 4．因为 f(x) f(x)6，y 3 ，所以函数y f(x)与y 的图象都关于点 x x x m (0，3)对称，所以(x  y )3m，故选B． i i i1 5．令 g(x) f(x)(3x1) ，所以 g(x) f(x)30 ，故 g(x) 在 R 上单调递减，又 g(2) f(2)50，所以当x2时，g(x)0，即 f(x)3x1，所以 f(x)3x1的解集 为(2，)，故选C． 6．设弦所在直线的斜率为 k，弦的端点A(x，y )，B(x，y )，则x x 2， y  y 4， 1 1 2 2 1 2 1 2 x2 y2  1  1 1 12 6 (x x )(x x ) (y  y )(y  y )  ， 两 式 相 减 ， 得 1 2 1 2  1 2 1 2 0 ， 所 以 x2 y2 12 6 2  2 1 12 6 数学参考答案·第1页（共9页） {#{QQABSYiQogigAAIAAQhCQwVACEOQkACACIoOQAAAMAAAgBFABAA=}#}2(x x ) 4(y  y ) y  y 1 1 1 2  1 2 0，所以k  1 2  ，经检验，k  满足题意，故选A． 12 6 x x 4 4 1 2 S n(n6) 7．易得数列{a } 为等差数列，且 a 2n7 ， S n2 6n ，则 b  n  ，令 n n n n a 2n7 n x2 6x 2(x2 7x21)  7 7  f(x) ，x0，则 f(x) 0，故 f(x)在 0，  ，  ， 上单调 2x7 (2x7)2  2 2  递增，没有最大值，因为b 1，b 9，b 8，结合数列的函数特征易得，当n4时，b 1 3 4 n 取得最小值，故选A． 1 97 1 97 3 1 1 1  1 1  8．bacos  12sin2   2sin2  2sin2 2 sin2  ，令 5 100 10 100 100 10 50 10 100 10 f(x)xsinx，则 f(x)1cosx≥0，所以函数 f(x)在R上单调递增，所以当x0时， 1 1 c 51 f(x) f(0)0，即有xsinx(x0)成立，所以 sin2 ，所以ba.因为   100 10 b 10 1 sin 5 51 1 cos2 xsin2x 1cos2 x  tan ，令g(x)tanxx，则g(x) 1 ≥0，所以函数 1 10 5 cos2x cos2x cos 5 g(x)在定义域内单调递增，所以当x0时，g(x)g(0)0，即有tanxx(x0)成立， 1 1 51 1 1 c 所以tan  ，即 tan 5tan 1，所以 1，又b0，所以cb，综上：cba， 5 5 10 5 5 b 故选B. 二、多项选择题（本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有 多项符合题目要求，全部选对的得5分，选对但不全的得2分，有选错的得0分） 题号 9 10 11 12 答案 ABD ABC ABD ABD 【解析】 2π π π π π 9 ．  2，m1 ，  2kπ，kπ ， 又 || ， 故  ， 即 π 12 6 2 6  π 2π 5π  5π π f(x)sin2x 1，故T  π，值域为[0，2]， f  sin2  11，故  6 2 12  12 6 2π  π 3π 13π C错误，当x ，π 时，2x  ， ，故D正确，故选ABD．      3  6  2 6  10．易得a0.05，产品长度在30mm以下的比例为(0.010.010.040.060.05)5 0.8585%，在 25mm 以下的比例为85%25%60%，因此，70%分位数一定位于 数学参考答案·第2页（共9页） {#{QQABSYiQogigAAIAAQhCQwVACEOQkACACIoOQAAAMAAAgBFABAA=}#}0.70.6 [25，30)内，由255 27，可以估计产品长度的样本数据的70%分位数是 0.850.6 27mm.由最高小矩形可知，众数估计值为22.5，平均数估计值为7.50.0512.50.05 17.50.222.50.327.50.2532.50.137.50.0523.25，故选ABC． 11．记A为事件“零件为第i(i1，2，3)机器加工”，记B为事件“任取一个零件为次品”，则 i P(A)0.2，P(A )0.35，P(A )0.45，对于A，即P(AB)P(A)P(B|A)0.10.2 1 2 3 1 1 1 0.02；对于B，P(B)P(A)P(B|A)P(A )P(B|A )P(A )P(B|A )0.10.20.08 1 1 2 2 3 3 P(A )P(B|A ) 0.080.35 1 0.350.080.450.084；对于C，P(A |B) 2 2   ；对于D， 2 P(B) 0.084 3 P(A )P(B|A ) 0.080.45 3 P(A |B) 3 3   ，故选ABD． 3 P(B) 0.084 7 1 lnx 12．对于A，∵x2时，x 2，∴2是 f(x)的一个下界，A正确；对于B， f(x) ， x x 1lnx 定义域为(0，)， f(x) ，令 f(x)0，∴xe，当x(0，e)时， f(x)0， x2 lne 1 当x(e，)时， f(x)0，当xe时， f(e)  ，当x0，有 f(x)，当 e e x， f(x)0，∴B正确；对于C， f(x)ex(x1)，令 f(x)0，∴x1，当 x(，1)， f(x)0， f(x)，当x(1，)， f(x)0， f(x)，∴当x1时， 1 f(1) ，当 x， f(x)，∴C 错误；对于 D，∵ 1≤cosx≤1， e 1 cosx 1 1 1 cosx ∴ ≤ ≤ ，又 ≤1， ≥1，∴1≤ ≤1，∴D正确， 1x2 1x2 1x2 1x2 1x2 1x2 故选ABD． 三、填空题（本大题共4小题，每小题5分，共20分） 题号 13 14 15 16 13 5 2 答案 [ 2，0)(0， 2] (，2] 10 4 【解析】 sin22sincos2cos2 13．sin2cos2cos2sin22sincos2cos2  sin2cos2 tan22tan2 962 13   ． tan21 91 10 数学参考答案·第3页（共9页） {#{QQABSYiQogigAAIAAQhCQwVACEOQkACACIoOQAAAMAAAgBFABAA=}#}p 14．由已知及抛物线的定义得点A到准线的距离为3，因此有2 3，解得 p2，故抛物 2 线方程为x2 4y，从而A(2 2，2).当△PAF 的周长最小即|PA||PF|的值最小，设 F 关于准线的对称点为 F ，则 F(0，3) ，连接 AF ，则 AF 与准线的交点即为使得 1 1 1 1 4 2  5 2 |PA||PF|的值最小的点P，此时可求得P ，1，所以k  ．   5   AP 4 15．由题意得方程 f(x)a2 0有三个不同的实数根，即方程 f(x)a2有三个不同的实数根， 所以函数y f(x)和函数ya2的图象有三个不同的交点．结合图象可得，要使两函数的 图象有三个不同的交点，则需满足0a2≤2，解得 2≤a0或0a≤ 2 ，所以实 数a的取值范围是[ 2，0)(0， 2]． 1lnx 1lnx 16．根据题意可知，x0，可得a≤e3x  1(x0)恒成立，令 f(x)e3x  1， x x 则a≤ f(x) ，现证明ex≥x1恒成立，设g(x)ex x1，g(x)ex 1，当g(x)0 min 时，解得x0，当x0时，g(x)0，g(x)单调递减，当x0时，g(x)0，g(x)单 调递增，故当 x0 时，函数 g(x) 取得最小值， g(0)0，所以 g(x)≥g(0)0 ，即 1lnx xe3x lnx1 ex x1≥0ex≥x1恒成立， f(x)e3x  1 1 x x elnx3x lnx1 lnx3x1lnx1  1≥ 12，所以 f(x) 2，即a≤2，所以实数 x x min a的取值范围是(，2]． 四、解答题（共70分．解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分10分） （1）解：∵a S S  S  S (n≥2)， n n n1 n n1 ∴( S  S )( S  S ) S  S (n≥2). n n1 n n1 n n1 又 S 0， S 0，∴ S  S 1， n n1 n n1 又S 1，∴数列{ S }是首项为1，公差为1的等差数列， 1 n ∴ S 1(n1)1n，故S n2. n n 当n≥2时，a S S n2 (n1)2 2n1， n n n1 当n1时，a 1符合上式， 1 ∴a 2n1． ………………………………………………………………（5分） n 数学参考答案·第4页（共9页） {#{QQABSYiQogigAAIAAQhCQwVACEOQkACACIoOQAAAMAAAgBFABAA=}#}1 1 1 1 （2）证明：∵b     (n≥2)， n S n2 n1 n n ∴T b b b n 1 2 n 1 1 1    12 22 n2 1 1 1 1 1 1 7 1 7          ， 12 22 2 3 n1 n 4 n 4 7 即T  ． ………………………………………………………………（10分） n 4 18．（本小题满分12分） 12345 解：（1）x  3， 5 n 5 (x x)(y  y) x y 5x y i i i i 相关系数r i1  i1  n (x i x)2 n (y i  y)2    5 x i 2 5x 2     5 y i 2 5y2   i1 i1  i1  i1  1483.85377 328.8 328.8    0.98， (5559)(409545772) 113090 336.3 因为y与x的相关系数r0.98，接近1， 所以y与x的线性相关程度很高，可用线性回归模型拟合y与x的关系． …………（6分） n 5 (x x)(y  y) x y 5x y i i i i （2）b ˆ  i1  i1 n 5 (x x)2 x2 5x2 i i i1 i1 1483.85377 328.8   32.88， 5559 10 aˆ yb ˆ x 7732.88321.64， 所以y与x的线性回归方程为yˆ 32.88x21.64， 又2023年对应的年份代码x6，yˆ 32.88621.64175.64， 所以预测2023年底贵州省刺梨产业的综合总产值为175.64亿元． ………………（12分） 19．（本小题满分12分） （1）证明：函数 f(x)ax的反函数为g(x)log x， a f(x)axlna， f(x )ax1lna， 1 数学参考答案·第5页（共9页） {#{QQABSYiQogigAAIAAQhCQwVACEOQkACACIoOQAAAMAAAgBFABAA=}#}1 1 g(x) ，g(x ) ， xlna 2 x lna 2 所以得ax1x ln2a1，两边同时取以a为底的对数得 2 log (ax1x ln2a)log 1， a 2 a log ax1 log x log (ln2a)0， a a 2 a 2ln(lna) 即x g(x ) 0． …………………………………………………………（6分） 1 2 lna （2）解：函数 f(x)ax与函数g(x)log x互为反函数，其函数图象关于yx对称， a 所以函数y f(x)与函数yg(x)的图象有两个交点等价于函数y f(x)与 yx的图象 有两个交点， 即方程lnax lnx有两个解， 即a>1时，xlnalnx， lnx 即方程lna 有两个解， x lnx 1lnx 令h(x) ， h(x) ， x x2 1lnx 当x(0，e)时，h(x) 0， x2 函数h(x)在x(0，e)上单调递增，且h(1)0， 1lnx 当x(e，)时，h(x) 0， x2 函数h(x)在x(e，)上单调递减， 且当x时，h(x)0， 1 所以当xe时，函数h(x)取到最大值h(e) ， e 1 所以0lna ， e 1 即1aee． ……………………………………………………………………（12分） 20．（本小题满分12分） （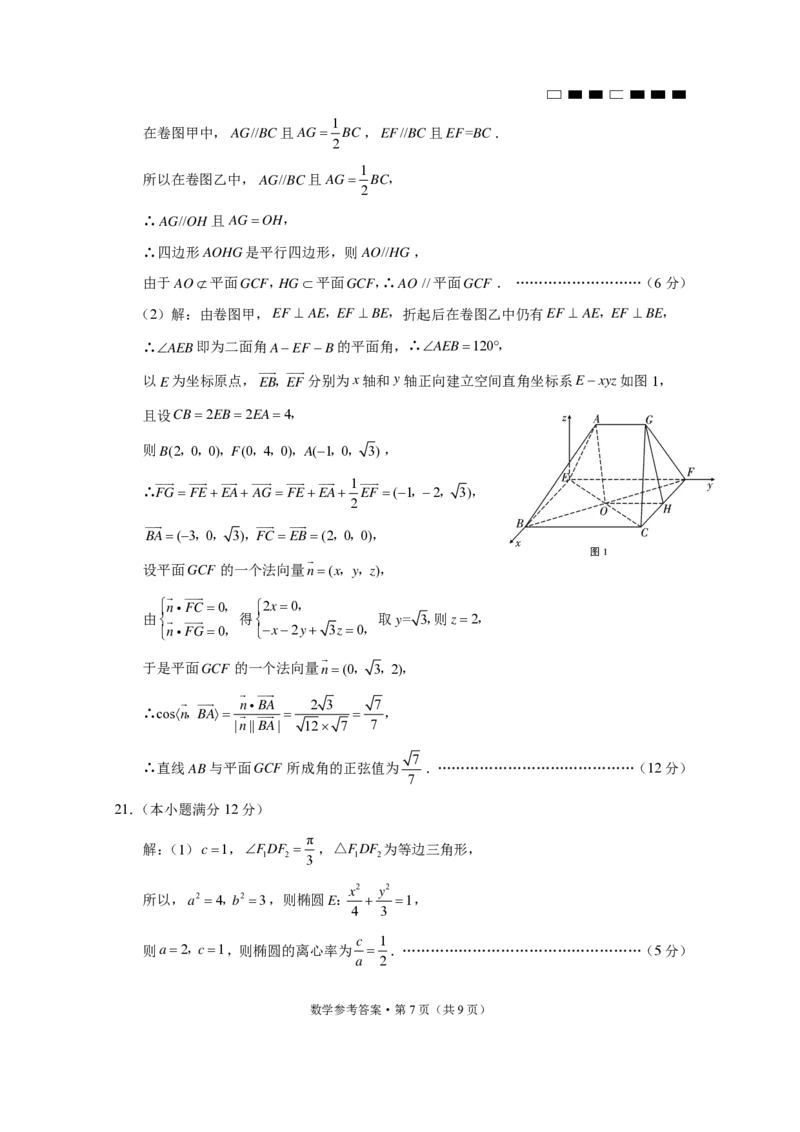1）证明：取线段CF中点H ，连接OH、GH ， 由卷图甲可知，四边形EBCF是矩形，且CB2EB， 1 ∴O是线段BF 与CE的中点，∴OH//BC且OH  BC， 2 数学参考答案·第6页（共9页） {#{QQABSYiQogigAAIAAQhCQwVACEOQkACACIoOQAAAMAAAgBFABAA=}#}1 在卷图甲中，AG//BC且AG BC，EF//BC且EF=BC． 2 1 所以在卷图乙中，AG//BC且AG BC， 2 ∴AG//OH 且AGOH， ∴四边形AOHG是平行四边形，则AO//HG， 由于AO平面GCF，HG平面GCF，∴AO //平面GCF ． ………………………（6分） （2）解：由卷图甲，EF  AE，EF BE，折起后在卷图乙中仍有EF  AE，EF BE， ∴AEB即为二面角AEF B的平面角，∴AEB120，   以E为坐标原点，EB，EF分别为x轴和y轴正向建立空间直角坐标系Exyz如图1， 且设CB2EB2EA4， 则B(2，0，0)，F(0，4，0)，A(1，0， 3)，       1 ∴FGFEEA AGFEEA EF (1，2， 3)， 2    BA(3，0， 3)，FC EB(2，0，0)， 图1  设平面GCF 的一个法向量n(x，y，z)，   nFC 0， 2x0， 由  得 取y= 3，则z2， nFG0， x2y 3z0，  于是平面GCF 的一个法向量n(0， 3，2)，     nBA 2 3 7 ∴cosn，BA     ， |n||BA| 12 7 7 7 ∴直线AB与平面GCF 所成角的正弦值为 ．……………………………………（12分） 7 21．（本小题满分12分） π 解：（1）c1，FDF  ，△FDF 为等边三角形， 1 2 3 1 2 x2 y2 所以，a2 4，b2 3，则椭圆E：  1， 4 3 c 1 则a2，c1，则椭圆的离心率为  ．……………………………………………（5分） a 2 数学参考答案·第7页（共9页） {#{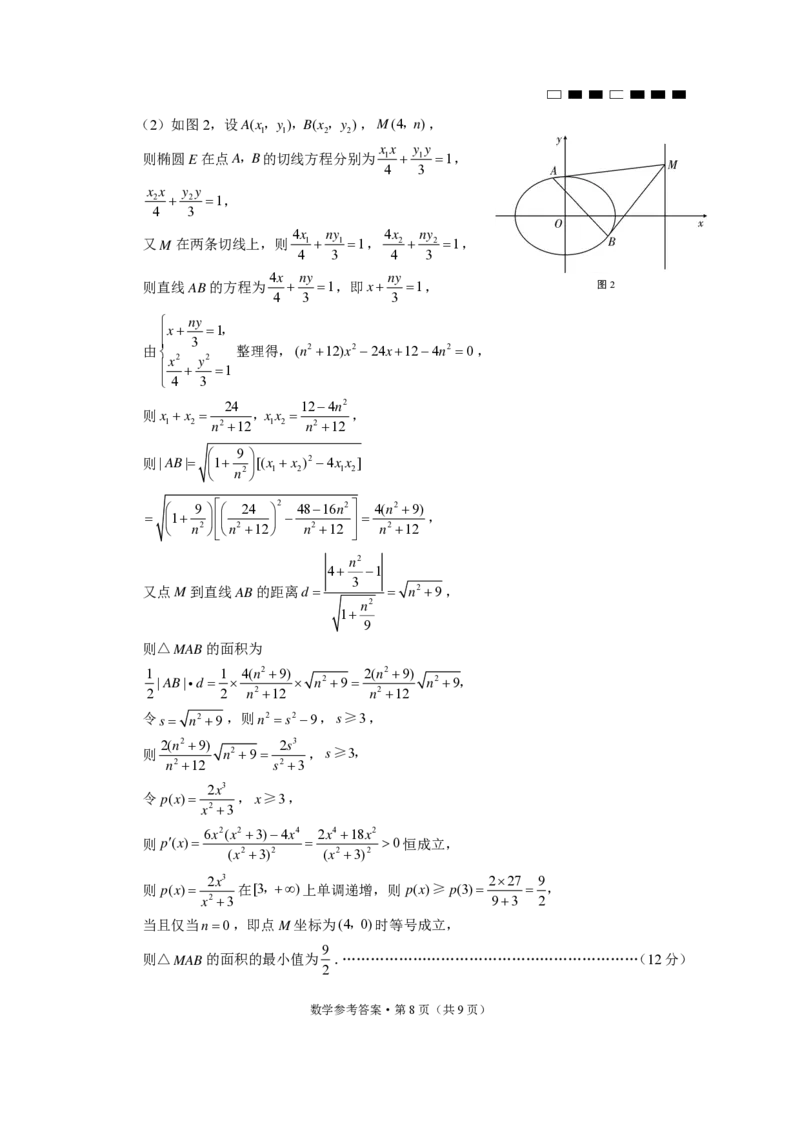QQABSYiQogigAAIAAQhCQwVACEOQkACACIoOQAAAMAAAgBFABAA=}#}（2）如图2，设A(x，y )，B(x，y )，M(4，n)， 1 1 2 2 xx y y 则椭圆E在点A，B的切线方程分别为 1  1 1， 4 3 x x y y 2  2 1， 4 3 4x ny 4x ny 又M 在两条切线上，则 1  1 1， 2  2 1， 4 3 4 3 4x ny ny 则直线AB的方程为  1，即x 1， 图2 4 3 3  ny x 1，   3 由 整理得，(n2 12)x2 24x124n2 0， x2 y2   1  4 3 24 124n2 则x x  ，xx  ， 1 2 n2 12 1 2 n2 12  9  则|AB| 1 [(x x )2 4xx ]  n2  1 2 1 2  9  24  2 4816n2 4(n2 9)  1      ，  n2 n2 12 n2 12  n2 12 n2 4 1 3 又点M到直线AB的距离d   n2 9， n2 1 9 则△MAB的面积为 1 1 4(n2 9) 2(n2 9) |AB|d    n2 9  n2 9， 2 2 n2 12 n2 12 令s n2 9，则n2 s2 9，s≥3， 2(n2 9) 2s3 则 n2 9  ，s≥3， n2 12 s2 3 2x3 令 p(x) ，x≥3， x2 3 6x2(x2 3)4x4 2x4 18x2 则 p(x)  0恒成立， (x2 3)2 (x2 3)2 2x3 227 9 则 p(x) 在[3，)上单调递增，则 p(x)≥p(3)  ， x2 3 93 2 当且仅当n0，即点M坐标为(4，0)时等号成立， 9 则△MAB的面积的最小值为 ．………………………………………………………（12分） 2 数学参考答案·第8页（共9页） {#{QQABSYiQogigAAIAAQhCQwVACEOQkACACIoOQAAAMAAAgBFABAA=}#}22．（本小题满分12分） 1 （1）解：F(x) f(x)g(x) x2 xaln(xa)的定义域为(a，+∞)， 2 a x(xa1) 又F(x)x1  ， xa xa 当1a0时，F(x)在(0，a+1)上单调递增，F(x)在(a，0)和(a+1，+∞)上单调递减； 当a1时，F(x)在(1，)上单调递减； 当a1时，F(x)在(a1，0)上单调递增，F(x)在(a，a1)和(0，)上单调递减． ………………………………………………………………………………………（5分） 1 （2）证明：由H(x) f(x)g(xa) x2 xalnx，x0， 2 a x2 xa 则H(x)x1  ，x0， x x 由题意知x ，x 是方程x2 xa0的两根， 1 2 1 1 因此x x 1，xx a，且 a0，0x  x 1， 1 2 1 2 4 1 2 2 (x a) 1 所以F(x )F(x ) aln 1  (x2 x2)(x x ) 1 2 (x a) 2 1 2 1 2 2 (x a) 1 aln 1  (x x )(x x 2)， (x a) 2 1 2 1 2 2 把x x 1，xx a代入，得 1 2 1 2 (x a) 1 (x xx ) 1 aln 1  (x x )xx ln 1 1 2  (x x ) (x a) 2 1 2 1 2 (x xx ) 2 1 2 2 2 1 2   1     1  xx  ln x 2   1  1  1    xx  ln   1 1   1 ln   1 1   1  ， 1 2    1 1   2x 1 x 2    1 2  x 2  2x 2 x 1  2x 1   x 1    1  1  1  1 要证F(x )F(x )，只需证明ln 1 ln 1 0， 1 2 x  2x x  2x 2 2 1 1  1  1  1  1 即ln 1 ln 1 ， x  2x x  2x 2 2 1 1  1  1 1   1  1 1  也即ln 1  1ln 1  1． x  2x  x  2x  2 2 1 1 1 1 1 令t  1，t  1，由0x  x 1，得2t t ， 1 x 2 x 1 2 2 2 1 1 2 1 设h(t)lnt t ，要证h(t )h(t )， 2 2 1 1 1 2t 因为h(t)   0，h(t)在(2，)上单调递减， t 2 2t 所以h(t )h(t )，即证． ……………………………………………………（12分） 2 1 数学参考答案·第9页（共9页） {#{QQABSYiQogigAAIAAQhCQwVACEOQkACACIoOQAAAMAAAgBFABAA=}#}