文档内容
2023—2024 学年度上学期高三年级 10 月月考试题
数学
第Ⅰ卷选择题(共60分)
一、选择题:(本大题共8小题,每小题 5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1. 已知集合 , , ,则实数 的值为( )
A. B. C. D.
2. 下列函数中,是偶函数且在 上单调递减的是( )
A. B. C. D.
3. 中,点 为 上的点,且 ,若 ,则 (
)
.
A B. C. D.
4. 中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减
一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走378里路,第一天
的
健步行走,从第二天起脚痛每天走 路程为前一天的一半,走了6天后到达目的地.”则该人第一天走
的路程为( )
A. 228里 B. 192里 C. 126里 D. 63里
5. 已知函数 满足 ,当 时, ,则 ( )
A. B. C. D.
6. 已知函数 图象的相邻两条对称轴之间的距离为 且关于点
第1页/共5页
学科网(北京)股份有限公司对称,则φ的值为( )
A. B. C. D.
7. 若函数 在区间 内单调递减,则实数 的取值范围为( )
A. B. C. D.
8. 给定函数 ,若函数 恰有两个零点,则 的取值范围是( )
A. B.
C. D.
二、多项选择题:(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,
有多项是符合题目要求的.全部选对得5分,有选错的得0分,部分选对的得2分)
9. 下列命题中正确的是( )
A. 若 ,则
B. 命题:“ ”的否定是“ ”
C. 已知函数 的定义域为 ,则函数 的定义域为
D. 若函数 则
10. 在 中,角A,B,C的对边分别为a,b,c,则下列结论正确的是( )
A. 若 ,则 一定是钝角三角形
B. 若 ,则 有两解
C. 若 ,则 为等腰三角形
第2页/共5页
学科网(北京)股份有限公司D. 若 为锐角三角形,则
11. 已知 的三个角A,B,C的对边分别为a,b,c, ,且 ,P是
AB边上的动点,则 的值可能为( ).
A. ﹣12 B. ﹣8 C. ﹣2 D. 0
12. 已知函数 ,则下列结论正确的是( )
A. 是周期为 的奇函数 B. 在 上为增函数
C. 在 内有20个极值点 D. 在 上恒成立的充要条件是
第Ⅱ卷 非选择题(共90分)
三、填空题:(本大题共4小题,每小题5分,共20分.把答案填在答题纸上.)
13. 已知单位向量 满足 若向量 则 _____.
14. 在等差数列 中, 为其前n项和.若 ,则数列 的公差d=______.
15. 在平面直角坐标系中,已知点 为角 终边上一点,若 , ,则
______.
16. 数列 满足 则数列 的前60项和为______.
四、解答题:(满分70分.解答应写出文字说明,证明过程或演算步骤,解答过程书写在答
题纸的对应位置.)
17. 已知函数 的最大值为1.
的
(1)求a 值;
第3页/共5页
学科网(北京)股份有限公司(2)将 的图象向上平移1个单位,再把图象上所有点的纵坐标缩短到原来的 (横坐标不变),再
把图象上所有点的横坐标缩短到原来的 (纵坐标不变),得到函数 的图象,在 中,角A,
B,C的对边分别为a,b,c,若 求 面积的最大值.
18. 已知等差数列 的公差 ,其前n项和为 ,若 ,且 , , 成等比数列.
(1)求数列 的通项公式;
(2)若 ,求 的取值范围.
19. 设函数 .
(1)若 ,求 在 处的切线方程;
(2)当 时,证明: .
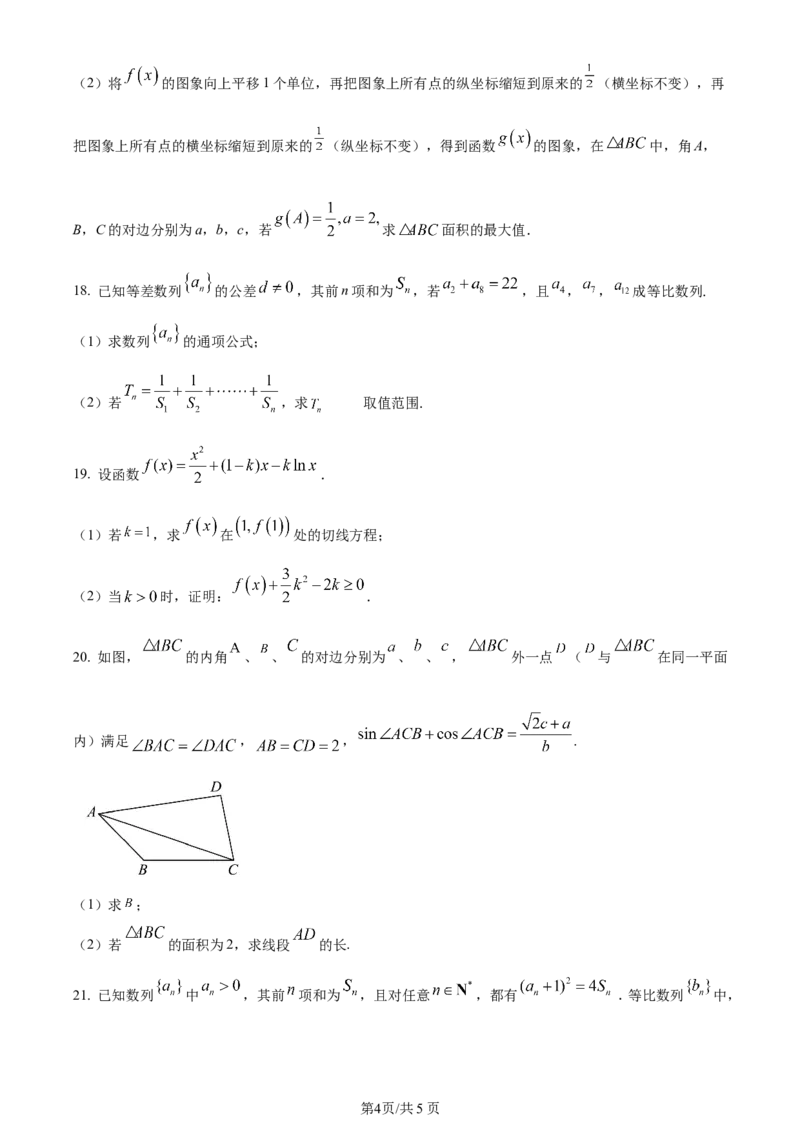
20. 如图, 的内角 、 、 的对边分别为 、 、 , 外一点 ( 与 在同一平面
内)满足 , , .
(1)求 ;
(2)若 的面积为2,求线段 的长.
21. 已知数列 中 ,其前 项和为 ,且对任意 ,都有 .等比数列 中,
第4页/共5页
学科网(北京)股份有限公司, .
(1)求数列 、 的通项公式;
(2)求数列 的前 项和 .
22. 已知函数 .
(1)当 时,求函数 的极小值;
(2)若 上,使得 成立,求 的取值范围.
第5页/共5页
学科网(北京)股份有限公司