文档内容
五年(2019-2023)年高考真题分项汇编
专题 05 立体几何(理科)(选填题)
立体几何在文科数高考中属于重点知识点,难度中等。包含题型主要是
1 空间几何体基本性质及表面积体积
2 空间几何题三视图
3 空间几何体内切球外接球的应用
4 空间几何体情景化应用
考点 01 空间几何体基本性质及表面积体积
一、单选题
1.(2023·全国·统考乙卷)已知圆锥PO的底面半径为 ,O为底面圆心,PA,PB为圆锥的母线,
,若 的面积等于 ,则该圆锥的体积为( )
A. B. C. D.
2.(2023·全国·统考甲卷)已知四棱锥 的底面是边长为4的正方形, ,
则 的面积为( )
A. B. C. D.
3.(2023·天津·统考高考真题)在三棱锥 中,线段 上的点 满足 ,线段 上的
点 满足 ,则三棱锥 和三棱锥 的体积之比为( )
A. B. C. D.
4.(2022·全国·统考高考乙卷)在正方体 中,E,F分别为 的中点,则( )
A.平面 平面 B.平面 平面
C.平面 平面 D.平面 平面
15.(2022·全国·统考高考甲卷)甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为 ,侧面积分
别为 和 ,体积分别为 和 .若 ,则 ( )
A. B. C. D.
6.(2022·北京·统考高考真题)已知正三棱锥 的六条棱长均为6,S是 及其内部的点构成的
集合.设集合 ,则T表示的区域的面积为( )
A. B. C. D.
7.(2021·全国·统考高考Ⅰ卷)已知圆锥的底面半径为 ,其侧面展开图为一个半圆,则该圆锥的母线
长为( )
A. B. C. D.
8.(2019·全国·统考高考Ⅲ卷)如图,点 为正方形 的中心, 为正三角形,平面 平面
是线段 的中点,则
A. ,且直线 是相交直线
B. ,且直线 是相交直线
C. ,且直线 是异面直线
D. ,且直线 是异面直线
二、填空题
9.(2023·全国新高考·Ⅱ卷)底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为
2,高为3的正四棱锥,所得棱台的体积为 .
10.(2020·全国·新高考Ⅱ卷)已知正方体ABCD-A B C D 的棱长为2,M、N分别为BB 、AB的中点,则三
1 1 1 1 1
棱锥A-NMD 的体积为
1
211.(2020·全国·统考高考Ⅱ卷)设有下列四个命题:
p :两两相交且不过同一点的三条直线必在同一平面内.
1
p :过空间中任意三点有且仅有一个平面.
2
p :若空间两条直线不相交,则这两条直线平行.
3
p :若直线l 平面α,直线m⊥平面α,则m⊥l.
4
则下述命题中所有真命题的序号是 .
① ② ③ ④
考点 02 空间几何体三视图
一、单选题
1.(2023·全国·统考高考乙卷)如图,网格纸上绘制的一个零件的三视图,网格小正方形的边长为1,则
该零件的表面积为( )
A.24 B.26 C.28 D.30
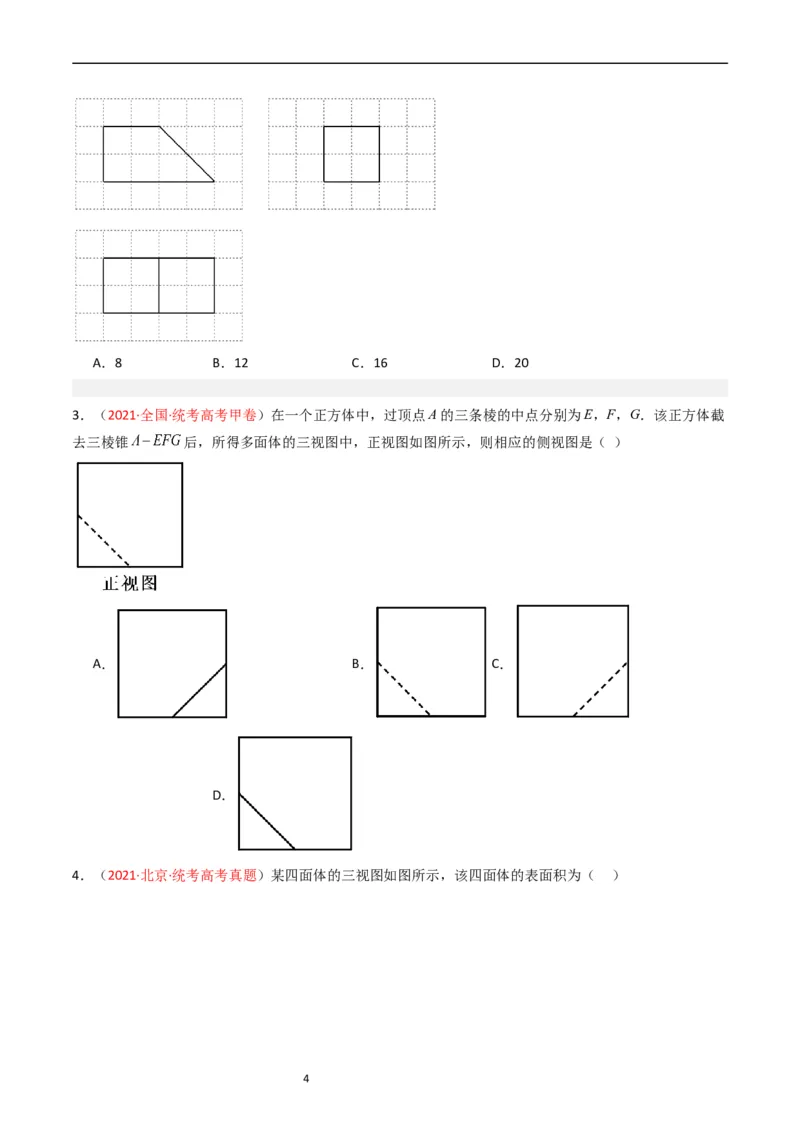
2.(2022·全国·统考高考甲卷)如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为
1,则该多面体的体积为( )
3A.8 B.12 C.16 D.20
3.(2021·全国·统考高考甲卷)在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截
去三棱锥 后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是( )
A. B. C.
D.
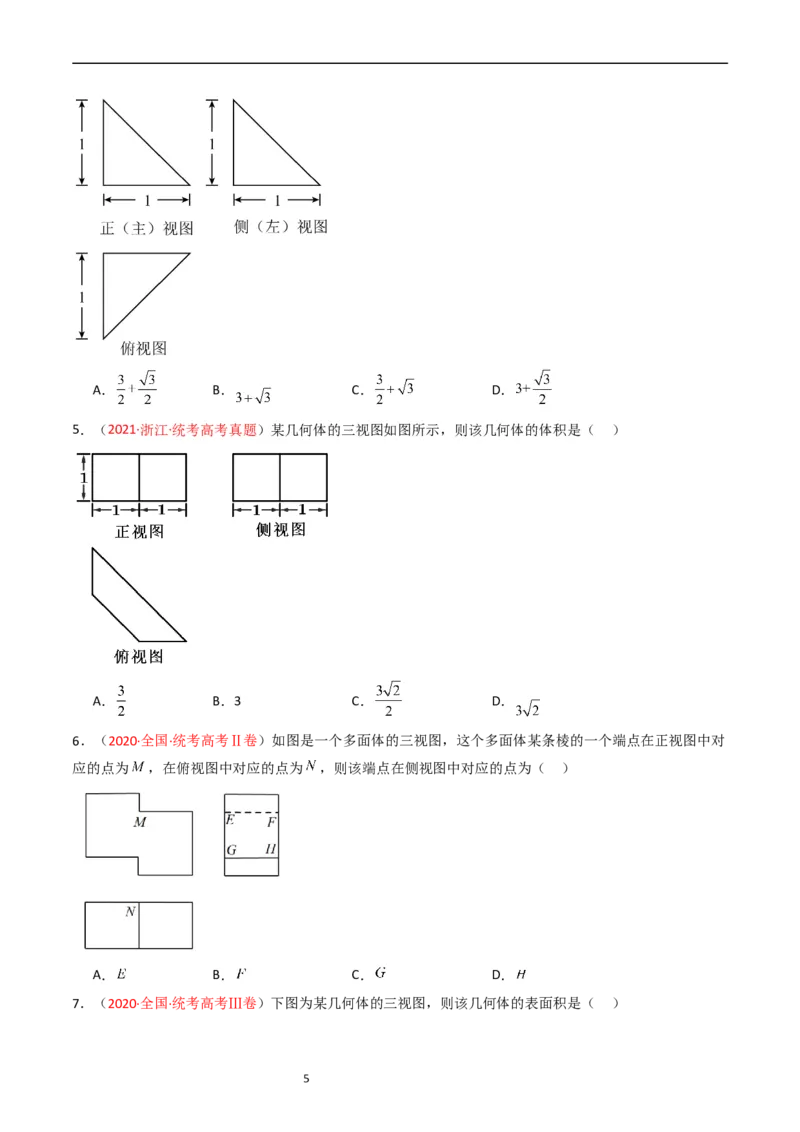
4.(2021·北京·统考高考真题)某四面体的三视图如图所示,该四面体的表面积为( )
4A. B. C. D.
5.(2021·浙江·统考高考真题)某几何体的三视图如图所示,则该几何体的体积是( )
A. B.3 C. D.
6.(2020·全国·统考高考Ⅱ卷)如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对
应的点为 ,在俯视图中对应的点为 ,则该端点在侧视图中对应的点为( )
A. B. C. D.
7.(2020·全国·统考高考Ⅲ卷)下图为某几何体的三视图,则该几何体的表面积是( )
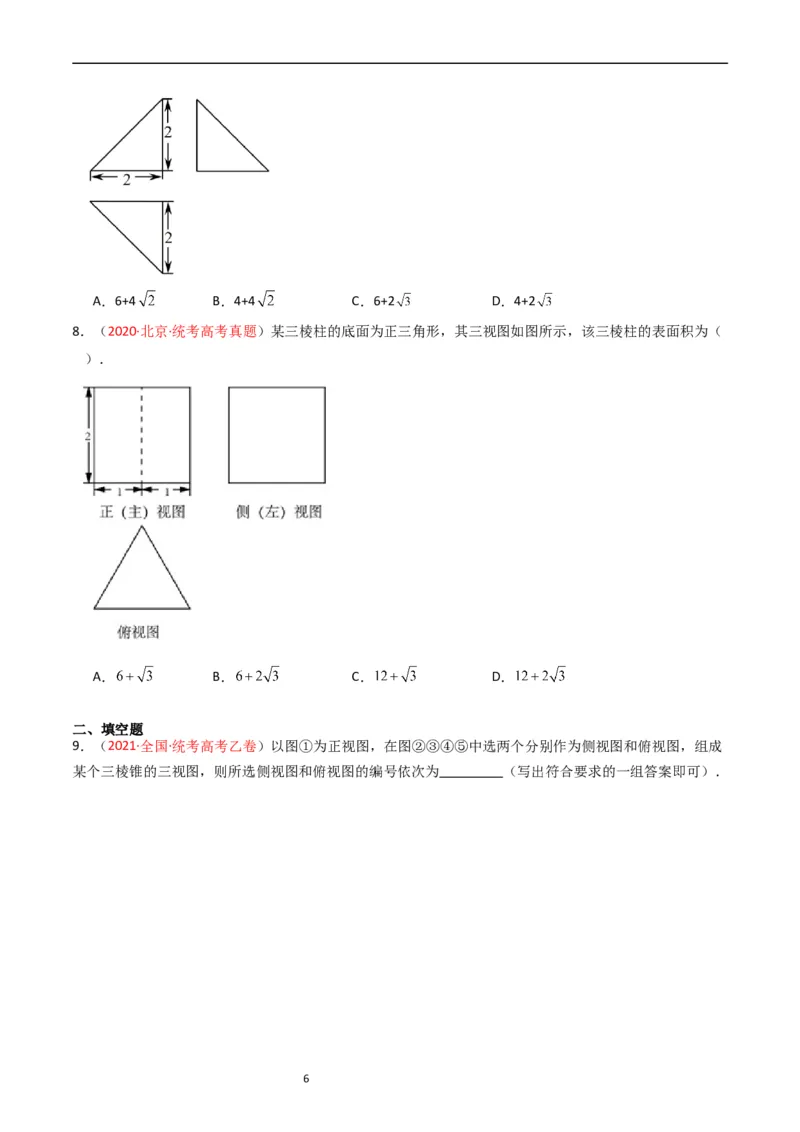
5A.6+4 B.4+4 C.6+2 D.4+2
8.(2020·北京·统考高考真题)某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为(
).
A. B. C. D.
二、填空题
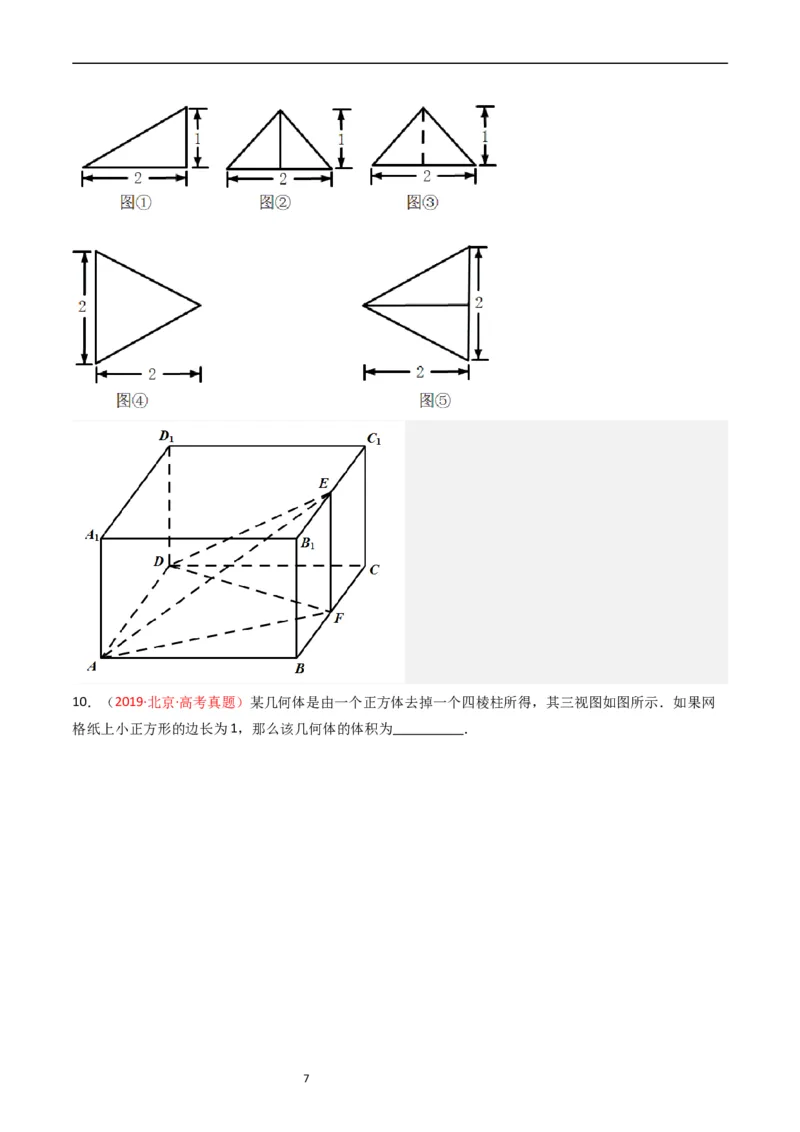
9.(2021·全国·统考高考乙卷)以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成
某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为 (写出符合要求的一组答案即可).
610.(2019·北京·高考真题)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网
格纸上小正方形的边长为1,那么该几何体的体积为 .
7考点 03 空间几何体内接球外切球问题
1.(2022·全国·统考高考乙卷)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球
面上,则当该四棱锥的体积最大时,其高为( )
A. B. C. D.
2.(2022·全国·统考新高考Ⅰ卷)已知正四棱锥的侧棱长为l,其各顶点都在同一球面上.若该球的体积为
,且 ,则该正四棱锥体积的取值范围是( )
A. B. C. D.
3.(2022·全国·统考新高考Ⅱ卷)已知正三棱台的高为1,上、下底面边长分别为 和 ,其顶点都
在同一球面上,则该球的表面积为( )
A. B. C. D.
4.(2021·全国·统考高考甲卷)已知A,B,C是半径为1的球O的球面上的三个点,且
,则三棱锥 的体积为( )
A. B. C. D.
5.(2020·全国·统考高考Ⅰ卷)已知 为球 的球面上的三个点,⊙ 为 的外接圆,若⊙
的面积为 , ,则球 的表面积为( )
8A. B. C. D.
6.(2019·全国·高考Ⅰ卷)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为
2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为
A. B. C. D.
二、填空题
7.(2023·全国·统考高考甲卷)在正方体 中,E,F分别为AB, 的中点,以EF为直
径的球的球面与该正方体的棱共有 个公共点.
8.(2019·全国·高考Ⅱ卷)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、
正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种
或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面
体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有 个
面,其棱长为 .
考点 04 空间几何题的情景化应用
1.(2023·北京·统考高考真题)坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以
勾勒出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两
个面是全等的等腰三角形.若 ,且等腰梯形所在的平面、等腰三角形所在的平面
与平面 的夹角的正切值均为 ,则该五面体的所有棱长之和为( )
A. B.
C. D.
92.(2022·全国·统考新高考Ⅱ卷)图1是中国古代建筑中的举架结构, 是桁,相邻桁的
水平距离称为步,垂直距离称为举,图2是某古代建筑屋顶截面的示意图.其中 是举,
是相等的步,相邻桁的举步之比分别为 .已知
成公差为0.1的等差数列,且直线 的斜率为0.725,则 ( )
A.0.75 B.0.8 C.0.85 D.0.9
3.(2022·天津·统考高考真题)如图,“十字歇山”是由两个直三棱柱重叠后的景象,重叠后的底面为正
方形,直三棱柱的底面是顶角为 ,腰为3的等腰三角形,则该几何体的体积为( )
A.23 B.24 C.26 D.27
4.(2021·全国·统考新高考Ⅱ卷)2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为
8848.86(单位:m),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,
现有A,B,C三点,且A,B,C在同一水平面上的投影 满足 , .由C
点测得B点的仰角为 , 与 的差为100;由B点测得A点的仰角为 ,则A,C两点到水平面
的高度差 约为( )( )
10A.346 B.373 C.446 D.473
5.(2021·全国·统考高考真题)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统
中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为 (轨道高度是指卫星到地球表
面的距离).将地球看作是一个球心为O,半径r为 的球,其上点A的纬度是指 与赤道平面所
成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为 ,记卫星信号覆盖
地球表面的表面积为 (单位: ),则S占地球表面积的百分比约为( )
A.26% B.34% C.42% D.50%
6.(2020·全国·统考高考Ⅰ卷)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,
以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与
底面正方形的边长的比值为( )
A. B. C. D.
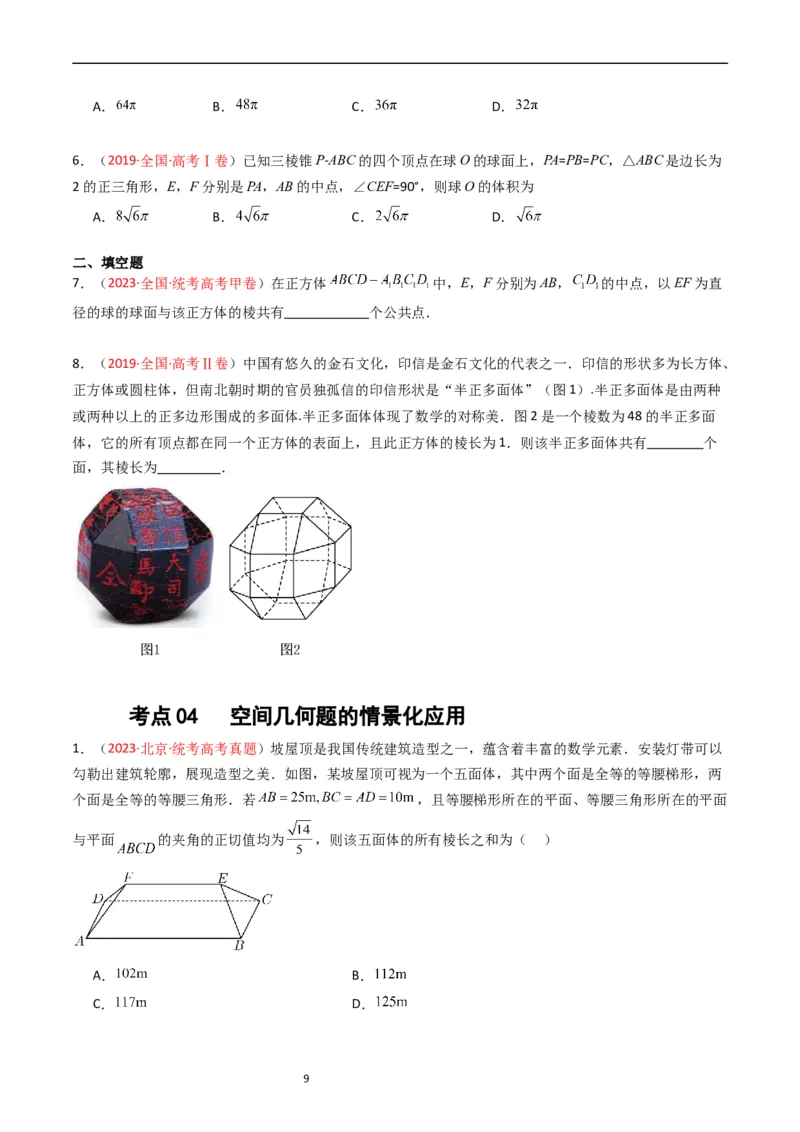
7.(2020·山东·统考高考真题)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面
的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所
成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平
行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )
11A.20° B.40°
C.50° D.90°
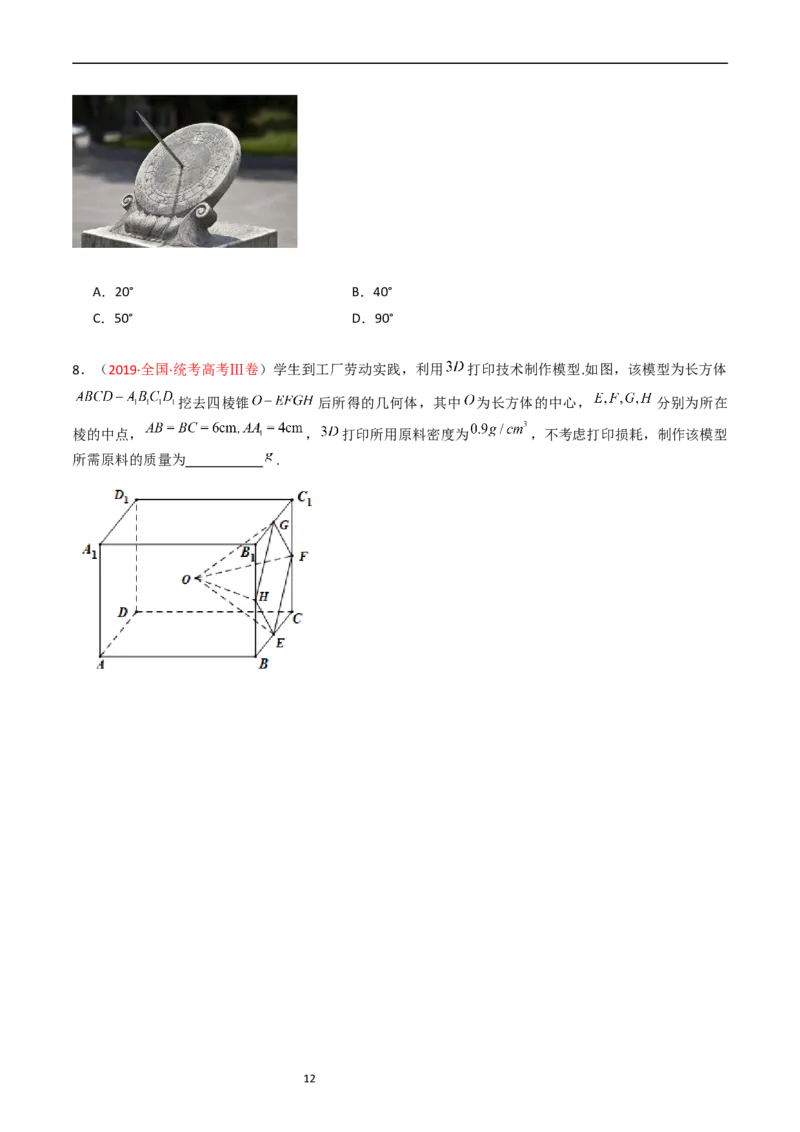
8.(2019·全国·统考高考Ⅲ卷)学生到工厂劳动实践,利用 打印技术制作模型.如图,该模型为长方体
挖去四棱锥 后所得的几何体,其中 为长方体的中心, 分别为所在
棱的中点, , 打印所用原料密度为 ,不考虑打印损耗,制作该模型
所需原料的质量为 .
12