文档内容
五年(2019-2023)年高考真题分项汇编
专题 09 三角函数
三角函数作为高考必考题,高考题型一般作为小题出现,偶尔也会出现解答题。小题部分一般是函数解析
式应用,求参数取值范围。
考点01 三角函数概念
考点02 三角函数恒等变形
考点03 三角函数图像及性质
考点04 三角函数综合应用
考点 01 三角函数概念
1.(2020年高考课标Ⅱ卷理科·第2题)若α为第四象限角,则 ( )
A.cos2α>0 B.cos2α<0 C.sin2α>0 D.sin2α<0
【答案】D
解析:方法一:由α为第四象限角,可得 ,
所以
此时 的终边落在第三、四象限及 轴的非正半轴上,所以
故选:D.
方法二:当 时, ,选项B错误;
当 时, ,选项A错误;
由 在第四象限可得: ,则 ,选项C错误,选项D正
确;
故选:D.
【点睛】本题主要考查三角函数的符号,二倍角公式,特殊角的三角函数值等知识,意在考查学生的
转化能力和计算求解能力.
2.(2020年高考课标Ⅰ卷理科·第9题)已知 ,且 ,则 ( )
1A. B. C. D.
【答案】A
【解析】 ,得 ,
即 ,解得 或 (舍去),
又 .
故选:A.
【点睛】本题考查三角恒等变换和同角间的三角函数关系求值,熟记公式是解题的关键,考查计算求
解能力,属于基础题.
3.(2021年高考全国甲卷理科·第9题)若 ,则 ( )
A. B. C. D.
【答案】A
解析:
,
, , ,解得 ,
, .
故选:A.
【点睛】关键点睛:本题考查三角函数的化简问题,解题的关键是利用二倍角公式化简求出 .
4.(2020年高考课标Ⅲ卷理科·第9题)已知2tanθ–tan(θ+ )=7,则tanθ= ( )
A.–2 B.–1 C.1 D.2
【答案】D
解析: , ,
令 ,则 ,整理得 ,解得 ,即 .
故选:D.
2【点睛】本题主要考查了利用两角和的正切公式化简求值,属于中档题
二 填空
1.(2020年浙江省高考数学试卷·第14题)已知圆锥展开图的侧面积为2π,且为半圆,则底面半径为
_______.
【答案】1
解析:设圆锥底面半径为 ,母线长为 ,则
,解得 .
2.(2021高考北京·第14题)若点 关于 轴对称点为 ,写出 的一
个取值为___.
【答案】 (满足 即可)
解析: 与 关于 轴对称,即 关于 轴对称,
,则 ,当 时,可取 的一个值为 .
故答案为: (满足 即可).
3.(2023年北京卷·第13题)已知命题 若 为第一象限角,且 ,则 .能说明p
为假命题的一组 的值为 __________, _________.
【答案】①. ②.
解析:因为 在 上单调递增,若 ,则 ,
取 ,
则 ,即 ,
令 ,则 ,
因为 ,则 ,
即 ,则 .
不妨取 ,即 满足题意.
3故答案为: .
4.(2020年浙江省高考数学试卷·第13题)已知 ,则 ________; ______.
【答案】(1). (2).
解析: ,
,
5.(2014高考数学陕西理科·第13题)设 ,向量 ,若 ∥ ,则
_______.
【答案】
解析: , ,因为 ,所以 ,
,即 .
考点 02 三角函数恒等变形
1.(2023年新课标全国Ⅰ卷·第8题)已知 ,则 ( ).
A. B. C. D.
【答案】B
解析:因为 ,而 ,因此 ,
则 ,
所以 .
故选:B
2.(2023年新课标全国Ⅱ卷·第7题)已知 锐角, ,则 ( ).
为
A. B. C. D.
4【答案】D
解析:因为 ,而 为锐角,
解得: .
故选:D.
3.(2021年高考浙江卷·第8题)已知 是互不相同 锐的角,则在 三个值
中,大于 的个数的最大值是 ( )
A.0 B.1 C.2 D.3
【答案】C
解析:法1:由基本不等式有 ,
同理 , ,
故 ,故 不可能均大于 .
取 , , ,则 ,
故三式中大于 的个数的最大值为2,故选C.
法2:不妨设 ,则 ,
由排列不等式可得:
,
而 ,
故 不可能均大于 .
取 , , ,则 ,
故三式中大于 的个数的最大值为2,故选C.
4.(2021年新高考Ⅰ卷·第6题)若 ,则 ( )
.
A B. C. D.
5【答案】C
解析:将式子进行齐次化处理得:
,故选C.
5.(2022新高考全国II卷·第6题)若 ,则 ( )
A. B.
.
C D.
【答案】C
解析:由已知得: ,
即: ,
,
即: 所以 , 故选:C
6.(2019·上海·第16题)已知 .
①存在 在第一象限,角 在第三象限;
②存在 在第二象限,角 在第四象限;
A. ①②均正确;B.①②均错误;C.①对,②错;D.①错,②对
【答案】D
【解析】(推荐)取特殊值检验法:例如:令 和 ,求 看是否存在.(考试中,若
有解时则认为存在,取多组解时发现没有解,则可认为不存在),选D.
(一般方法)
设 则 ;
以 为主元则可写成: 其判别式 ;
设函数 ,并设 ,则
6即 单调递减;
而 ,故 的零点在 上,设为 ;
则当 时, ,当 时, ;
故存在 使得
而对方程 ,根据韦达定理,
存在 时,而 使得对应的 存在,而此时 ,故此时 必为负数,即 在Ⅱ
或Ⅳ象限;
也同样存在 ,使得对应的 存在,此时 ,故此时必存在一个 值为负数,另一个
为正数,即 在Ⅱ、Ⅳ象限或Ⅰ、Ⅲ象限均可,故选D.
【点评】本题主要考三角恒等变换、不等式综合.
7.(2019·全国Ⅱ·理·第10题)已知 , ,则 ( )
A. B. C. D.
【答案】B
【解析】∵ ,∴ . ,∴ , ,
∴ , 又 , ∴ , , 又 , ∴
sin2cos21 sin0
,故选B.
【点评】利用二倍角公式得到正余弦关系,利用角范围及正余弦平方和为1关系得出答案.本题为三
角函数中二倍角公式、同角三角函数基本关系式的考查,中等难度,判断正余弦正负,运算准确性是
关键,题目不难,需细心,解决三角函数问题,研究角的范围后得出三角函数值的正负,很关键,切
记不能凭感觉.
二 填空
1.(2022年浙江省高考数学试题·第13题)若 ,则 __________,
_________.
7【答案】 ①. ②.
解析: ,∴ ,即 ,
即 ,令 , ,
则 ,∴ ,即 ,
∴ ,
则 .
故答案为: ; .
2.(2020江苏高考·第8题)已知 ,则 的值是____.
【答案】
【解析】
,故答案为:
3.(2019·江苏·第13题)已知 ,则 的值是 .
【答案】
【解析】法1: ,解得, 或 .
所以 =
= = .
8法2:令 ,则 ,即 ,
解得 ,所以 .
考点 03 三角函数图像及性质
1.(2023年全国乙卷理科·第6题)已知函数 在区间 单调递增,直线 和
为函数 的图像的两条相邻对称轴,则 ( )
A. B. C. D.
【答案】D
解析:因为 在区间 单调递增,
所以 ,且 ,则 , ,
当 时, 取得最小值,则 , ,
则 , ,不妨取 ,则 ,
则 ,
故选:D.
2.(2023年全国甲卷理科·第10题)函数 的图象由函数 的图象向左平移 个单
位长度得到,则 的图象与直线 的交点个数为 ( )
A.1 B.2 C.3 D.4
【答案】C
9解析:因为 向左平移 个单位所得函数为
,所以 ,
而 显然过 与 两点,
作出 与 的部分大致图像如下,
考虑 ,即 处 与 的大小关系,
当 时, , ;
当 时, , ;
当 时, , ;
所以由图可知, 与 的交点个数为 .
故选:C.
3.(2021年新高考Ⅰ卷·第4题)下列区间中,函数 单调递增的区间是 ( )
A. B. C. D.
【答案】A
解析:因为函数 的单调递增区间为 ,
对于函数 ,由 ,
10解得 ,
取 ,可得函数 的一个单调递增区间为 ,
则 , ,A选项满足条件,B不满足条件;
取 ,可得函数 的一个单调递增区间为 ,
且 , ,CD选项均不满足条件,故选A.
2π
C : y sin 2x
C : y cosx 2 3
4.(2017年高考数学新课标Ⅰ卷理科·第9题)已知曲线 1 , ,则下面结论正
确的是 ( )
π
C
A.把 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移 6 个单位长度,得到
C
曲线 2
π
C
B.把 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移12个单位长度,得到
C
曲线 2
1 π
C
C.把 1上各点的横坐标缩短到原来的 2 倍,纵坐标不变,再把得到的曲线向右平移 6 个单位长度,得到
C
曲线 2
1 π
C
D.把 1上各点的横坐标缩短到原来的2 倍,纵坐标不变,再把得到的曲线向左平移12个单位长度,得
C
到曲线 2
【答案】 D
C ,C C C
【解析】因为 1 2函数名不同,所以先将 2利用诱导公式转化成与 1相同的函数名,则
2π 2π π π 1
C : y sin 2x cos 2x cos 2x
2 3 3 2 6 ,则由 C 1上各点的横坐标缩短到原来的 2
π
倍变为 y sin2x ,再将曲线向左平移12个单位得到 C 2,故选D.
5.(2020年高考课标Ⅰ卷理科·第7题)设函数 在 的图像大致如下图,则f(x)的
最小正周期为 ( )
11A. B. C. D.
【答案】C
【解析】由图可得:函数图象过点 ,
将它代入函数 可得:
又 是函数 图象与 轴负半轴的第一个交点,
所以 ,解得:
所以函数 的最小正周期为 故选:C
6.(2022高考北京卷·第5题)已知函数 ,则 ( )
A. 在 上单调递减 B. 在 上单调递增
C. 在 上单调递减 D. 在 上单调递增
【答案】C解析:因为 .
对于A选项,当 时, ,则 在 上单调递增,A错;
对于B选项,当 时, ,则 在 上不单调,B错;
对于C选项,当 时, ,则 在 上单调递减,C对;
12对于D选项,当 时, ,则 在 上不单调,D错.故选,C.
7.(2022年高考全国甲卷数学(理)·第12题)已知 ,则 ( )
A. B. C. D.
【答案】A
【解析】因为 ,因为当
所以 ,即 ,所以 ;设 ,
,所以 在 单调递增,则 ,所以 ,
所以 ,所以 ,故选:A
8.(2022年浙江省高考数学试题·第6题)为了得到函数 的图象,只要把函数
图象上所有的点 ( )
A.向左平移 个单位长度 B.向右平移 个单位长度
C.向左平移 个单位长度 D.向右平移 个单位长度
【答案】D解析:因为 ,所以把函数 图象上的
所有点向右平移 个单位长度即可得到函数 的图象.故选,D.
9.(2022新高考全国I卷·第6题)记函数 的最小正周期为T.若
,且 的图象关于点 中心对称,则 ( )
A.1 B. C. D.3
【答案】A解析: 由函数的最小正周期T满足 ,得 ,解得 ,
13又因为函数图象关于点 对称,所以 ,且 ,
所以 ,所以 , ,
所以 . 故选:A
10.(2021高考北京·第7题)函数 是 ( )
A.奇函数,且最大值为2 B.偶函数,且最大值为2
C.奇函数,且最大值为 D.偶函数,且最大值为
【答案】D
解析:由题意, ,所以该函数为偶函数,
又 ,
所以当 时, 取最大值 . 故选:D.
11.(2020天津高考·第8题)已知函数 .给出下列结论:
① 的最小正周期为 ;
② 是 的最大值;
③把函数 的图象上所有点向左平移 个单位长度,可得到函数 的图象.
其中所有正确结论的序号是 ( )
A.① B.①③ C.②③ D.①②③
【答案】B
【解析】因为 ,所以周期 ,故①正确;
,故②不正确;
将函数 的图象上所有点向左平移 个单位长度,得到 的图象,
故③正确.故选:B.
12.(2019·天津·理·第7题)已知函数 是奇函数,将 的
14图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为 .若 的最
小正周期为 ,且
,则 ( )
A. B. C. D.2
【答案】答案:C
解析: 是奇函数, ,又因为 ,
,因为 的最小正周期为 ,且 ,所以 , ,
,可得 , , .
( )
13.(2019·全国Ⅱ·理·第9题)下列函数中,以 为周期且在区间 单调递增的是
( )
A. B. C. D.
【答案】A
【解析】因为y sin|x|图象如下图,知其不是周期函数,排除D;因为y cos x cosx,周期为
,排除C,作出 图象,由图象知,其周期为 ,在区间 单调递增,A正确;
y cos2x
2 2
作出 的图象,由图象知,其周期为 ,在区间 单调递减,排除B,故选A.
y sin2x
2
15【点评】本题主要考查三角函数图象与性质,渗透直观想象、逻辑推理等数学素养.画出各函数图象,
即可做出选择.利用二级结论:①函数y f(x) 的周期是函数y f(x)周期的一半;②
y sinx 不是周期函数;③函数 ,再利用降幂公式及三角函数公式法求三角
函数的周期,例如, ,所以周期 .
14.(2019·全国Ⅰ·理·第11题)关于函数 有下述四个结论:
① 是偶函数② 在区间 单调递增
③ 在 有4个零点④ 的最大值为2
其中所有正确结论的编号是 ( )
A.①②④ B.②④ C.①④ D.①③
【答案】答案:C
解析:作出函数 的图象如图所示,
由图可知, 是偶函数,①正确, 在区间 单调递减,②错误,
在 有3个零点,③错误; 的最大值为2,④正确,故选C.
ysinx
O
ysinx
3π 5π 2π 3π π π O π π 3π 2π 5π 3π
2 2 2 2 2 2
ysinxsinx
O
二 填空
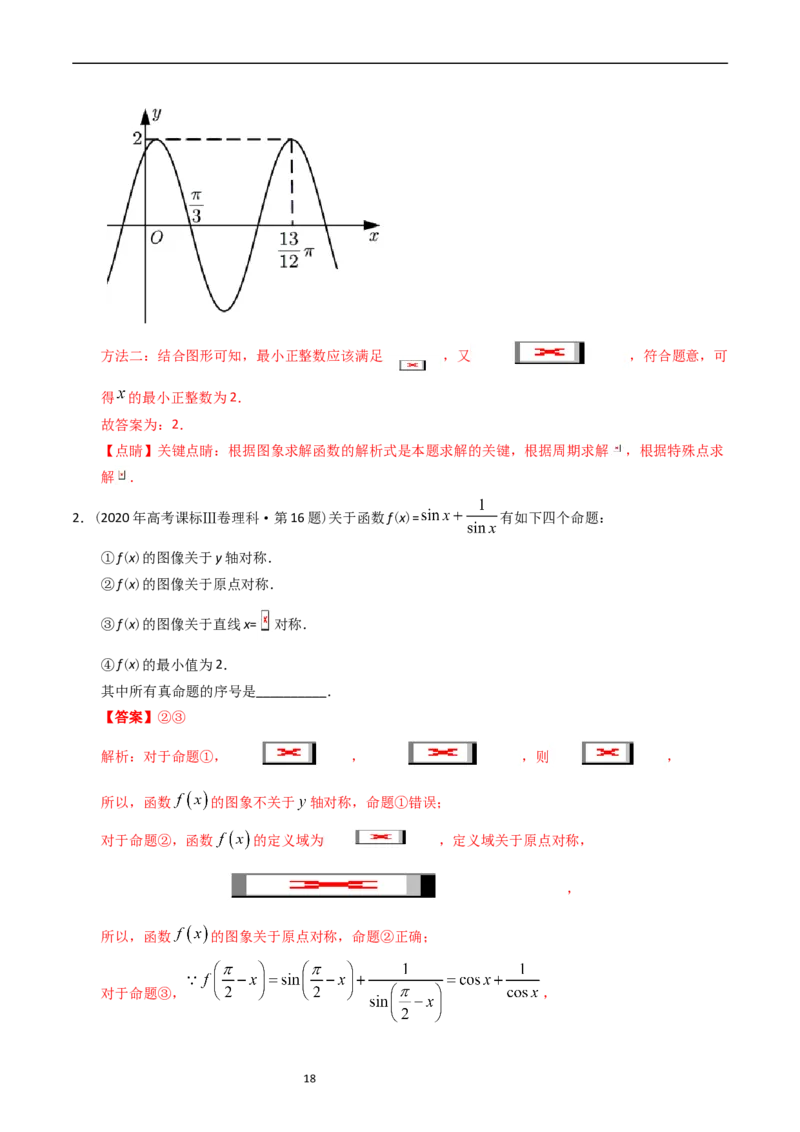
1.(2021年高考全国甲卷理科·第16题)已知函数 的部分图像如图所示,则满足条
件 的最小正整数x为________.
16【答案】2
解析:由图可知 ,即 ,所以 ;
由五点法可得 ,即 ;
所以 .
因为 , ;
所以由 可得 或 ;
因为 ,所以,
方法一:结合图形可知,最小正整数应该满足 ,即 ,
解得 ,令 ,可得 ,
可得 的最小正整数为2.
17方法二:结合图形可知,最小正整数应该满足 ,又 ,符合题意,可
得 的最小正整数为2.
故答案为:2.
【点睛】关键点睛:根据图象求解函数的解析式是本题求解的关键,根据周期求解 ,根据特殊点求
解 .
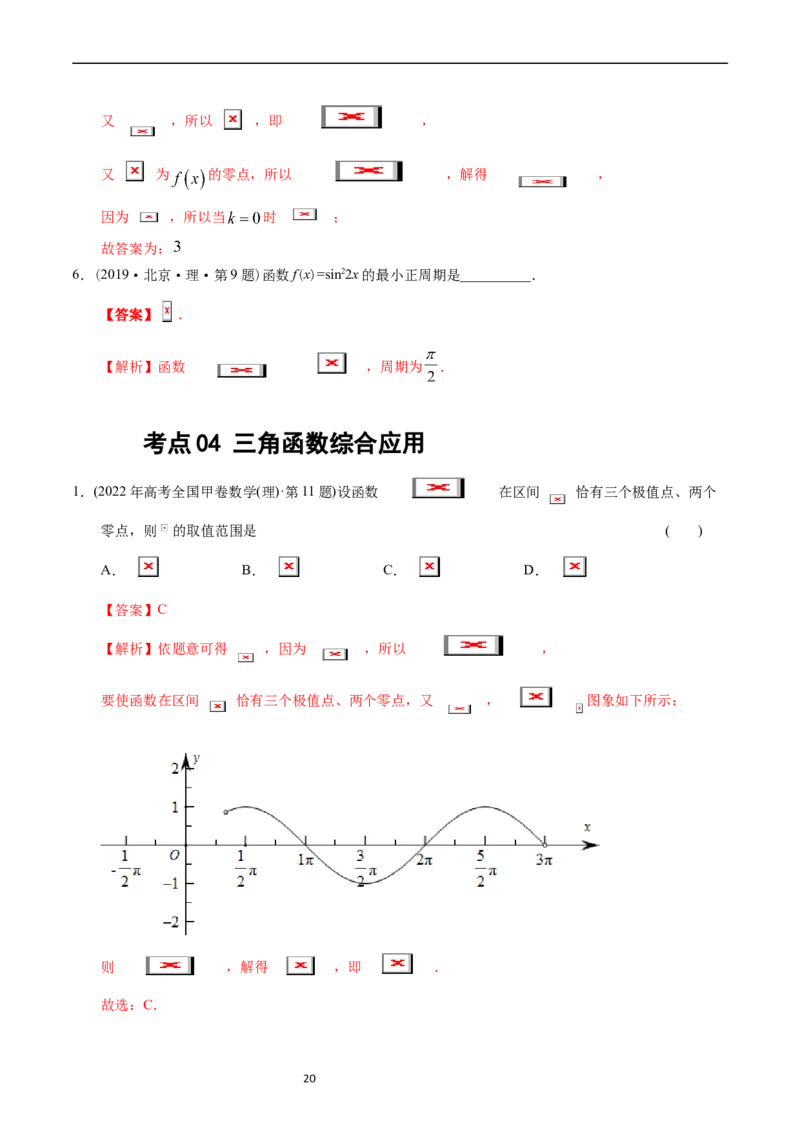
2.(2020年高考课标Ⅲ卷理科·第16题)关于函数f(x)= 有如下四个命题:
①f(x)的图像关于y轴对称.
②f(x)的图像关于原点对称.
③f(x)的图像关于直线x= 对称.
④f(x)的最小值为2.
其中所有真命题的序号是__________.
【答案】②③
解析:对于命题①, , ,则 ,
所以,函数 的图象不关于 轴对称,命题①错误;
对于命题②,函数 的定义域为 ,定义域关于原点对称,
,
所以,函数 的图象关于原点对称,命题②正确;
对于命题③, ,
18,则 ,
所以,函数 的图象关于直线 对称,命题③正确;
对于命题④,当 时, ,则 ,
命题④错误.
故答案为:②③.
【点睛】本题考查正弦型函数的奇偶性、对称性以及最值的求解,考查推理能力与计算能力,属于中
等题.
3.(2020江苏高考·第10题)将函数 的图象向右平移 个单位长度,则平移后的图象中与
轴最近的对称轴的方程是____.
【答案】
【解析】 , ,
当 时 ,故答案为:
4.(2020北京高考·第14题)若函数 的最大值为2,则常数 的一个取值为
________.
【答案】 ( 均可)
【解析】因为 ,
所以 ,解得 ,故可取 .故答案为: ( 均可).
5.(2022年高考全国乙卷数学(理)·第15题)记函数 的最小正周
期为T,若 , 为 的零点,则 的最小值为____________.
【答案】3
解析:因为 ,( , )
所以最小正周期 ,因为 ,
19又 ,所以 ,即 ,
又 为 的零点,所以 ,解得 ,
因为 ,所以当 时 ;
故答案为:
6.(2019·北京·理·第9题)函数f(x)=sin22x的最小正周期是__________.
【答案】 .
【解析】函数 ,周期为 .
考点 04 三角函数综合应用
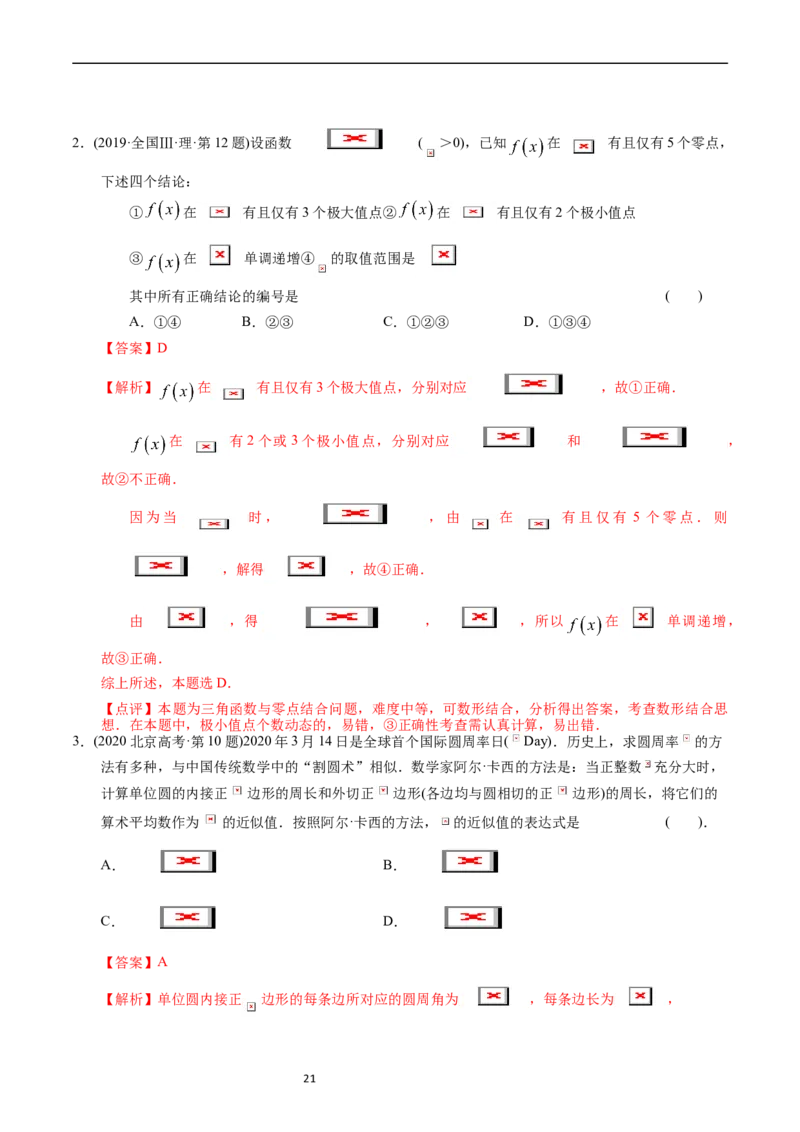
1.(2022年高考全国甲卷数学(理)·第11题)设函数 在区间 恰有三个极值点、两个
零点,则 的取值范围是 ( )
A. B. C. D.
【答案】C
【解析】依题意可得 ,因为 ,所以 ,
要使函数在区间 恰有三个极值点、两个零点,又 , 图象如下所示:
则 ,解得 ,即 .
故选:C.
202.(2019·全国Ⅲ·理·第12题)设函数 ( >0),已知 在 有且仅有5个零点,
下述四个结论:
① 在 有且仅有3个极大值点② 在 有且仅有2个极小值点
③ 在 单调递增④ 的取值范围是
其中所有正确结论的编号是 ( )
A.①④ B.②③ C.①②③ D.①③④
【答案】D
【解析】 在 有且仅有3个极大值点,分别对应 ,故①正确.
在 有2个或3个极小值点,分别对应 和 ,
故②不正确.
因为当 时, ,由 在 有且仅有 5 个零点.则
,解得 ,故④正确.
由 ,得 , ,所以 在 单调递增,
故③正确.
综上所述,本题选D.
【点评】本题为三角函数与零点结合问题,难度中等,可数形结合,分析得出答案,考查数形结合思
想.在本题中,极小值点个数动态的,易错,③正确性考查需认真计算,易出错.
3.(2020北京高考·第10题)2020年3月14日是全球首个国际圆周率日( Day).历史上,求圆周率 的方
法有多种,与中国传统数学中的“割圆术”相似.数学家阿尔·卡西的方法是:当正整数 充分大时,
计算单位圆的内接正 边形的周长和外切正 边形(各边均与圆相切的正 边形)的周长,将它们的
算术平均数作为 的近似值.按照阿尔·卡西的方法, 的近似值的表达式是 ( ).
A. B.
C. D.
【答案】A
【解析】单位圆内接正 边形的每条边所对应的圆周角为 ,每条边长为 ,
21所以,单位圆的内接正 边形的周长为 ,
单位圆的外切正 边形的每条边长为 ,其周长为 ,
,则 .
故选:A.
二 填空
1.(2022年浙江省高考数学试题·第17题)设点P在单位圆的内接正八边形 的边 上,则
的取值范围是_______.
【答案】
解析:以圆心为原点, 所在直线为 轴, 所在直线为 轴建立平面直角坐标系,如图所示:
则 ,
,设 ,于是 ,
因为 ,所以 ,故 的取值范围是
.
故答案为: .
2.(2023年新课标全国Ⅰ卷·第15题)已知函数 在区间 有且仅有3个零
点,则 的取值范围是________.
【答案】
22解析:因为 ,所以 ,
令 ,则 有3个根,
令 ,则 有3个根,其中 ,
结合余弦函数 的图像性质可得 ,故 ,
故答案为: .
3.(2023年新课标全国Ⅱ卷·第16题)已知函数 ,如图A,B是直线 与曲线
的两个交点,若 ,则 ______.
【答案】
解析:设 ,由 可得 ,
由 可知, 或 , ,由图可知,
,即 , .
因为 ,所以 ,即 , .
所以 ,
所以 或 ,
又因为 ,所以 , .
23故答案为: .
三 解答题
1 (2019·浙江·第18题)设函数 , .
(Ⅰ)已知 ,函数 是偶函数,求 的值;
(Ⅱ)求函数 的值域.
【答案】【意图】本题主要考查三角函数及其恒等变换等基础知识,同时考查运算求解能力。满分14
分。
【 解 析 】 (Ⅰ ) 解 法 一 : 因 为 是 偶 函 数 , 所 以 , 对 任 意 实 数 都 有
,
即 ,故 ,所以 ,又 ,
因此, 或 .
解法二:根据诱导公式, , ,因为 是偶函数,
,
所以
(Ⅱ)
.因此,函数的值域是 .
.
2.(2021年高考浙江卷·第18题)设函数 .
(1)求函数 的最小正周期;
(2)求函数 在 上的最大值.
【答案】(1) ;(2) .
解析:(1)由辅助角公式得 ,
24则 ,
所以该函数的最小正周期 ;
(2)由题意,
,
由 可得 ,所以当 即 时,函数取最大值 .
3 (2023年北京卷·第17题)设函数 .
(1)若 ,求 的值.
(2)已知 在区间 上单调递增, ,再从条件①、条件②、条件③这三个条件
中选择一个作为已知,使函数 存在,求 的值.
条件①: ;
条件②: ;
条件③: 区间 上单调递减.
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个
解答计分.
【答案】(1) .
(2)条件①不能使函数 存在;条件②或条件③可解得 , .
解析:(1)因为
25所以 ,
因为 ,所以 .
(2)因为 ,
所以 ,所以 的最大值为 ,最小值为 .
若选条件①:因为 的最大值为 ,最小值为 ,所以 无解,故条件
①不能使函数 存在;
若选条件②:因为 在 上单调递增,且 ,
所以 ,所以 , ,
所以 ,
又因为 ,所以 ,
所以 ,
所以 ,因为 ,所以 .
所以 , ;
若选条件③:因为 在 上单调递增,在 上单调递减,
所以 在 处取得最小值 ,即 .
以下与条件②相同.
26