文档内容
五年(2019-2023)年高考真题分项汇编
专题 10 解三角形
解三角形作为高考必考题,高考题型一般作为1小1大或者是2小1大模式。
考点01 正弦余弦定理应用
考点02 三角形中面积周长应用
考点03 结构不良结构
考点 01 正弦余弦定理应用
1.(2023年北京卷·第7题)在 中, ,则 ( )
A. B. C. D.
2.(2020年高考课标Ⅲ卷理科·第7题)在△ABC中,cosC= ,AC=4,BC=3,则cosB= ( )
A. B. C. D.
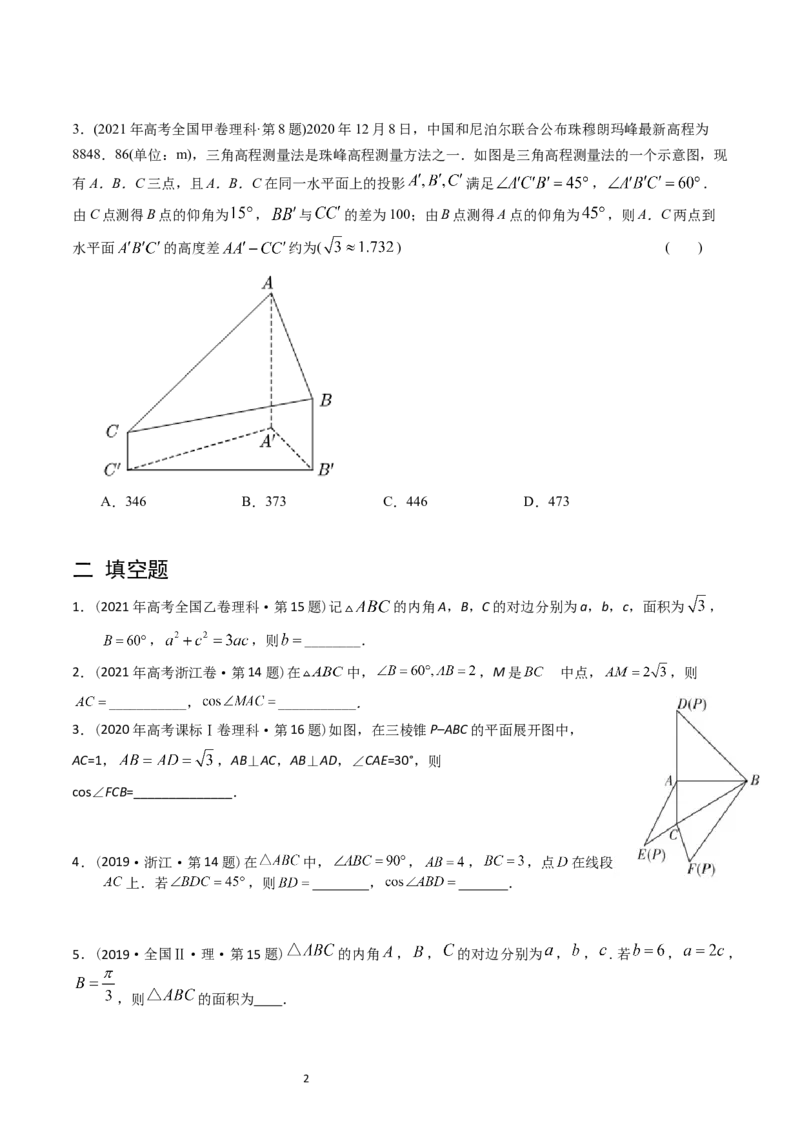
2.(2021年高考全国乙卷理科·第9题)魏晋时刘徽撰写的《海岛算经》是关测量的数学著作,其中第一题
是测海岛的高.如图,点 , , 在水平线 上, 和 是两个垂直于水平面且等高的测量
标杆的高度,称为“表高”, 称为“表距”, 和 都称为“表目距”, 与 的差称
为“表目距的差”则海岛的高 ( )
( )
A. 表高 B. 表高
C. 表距 D. 表距
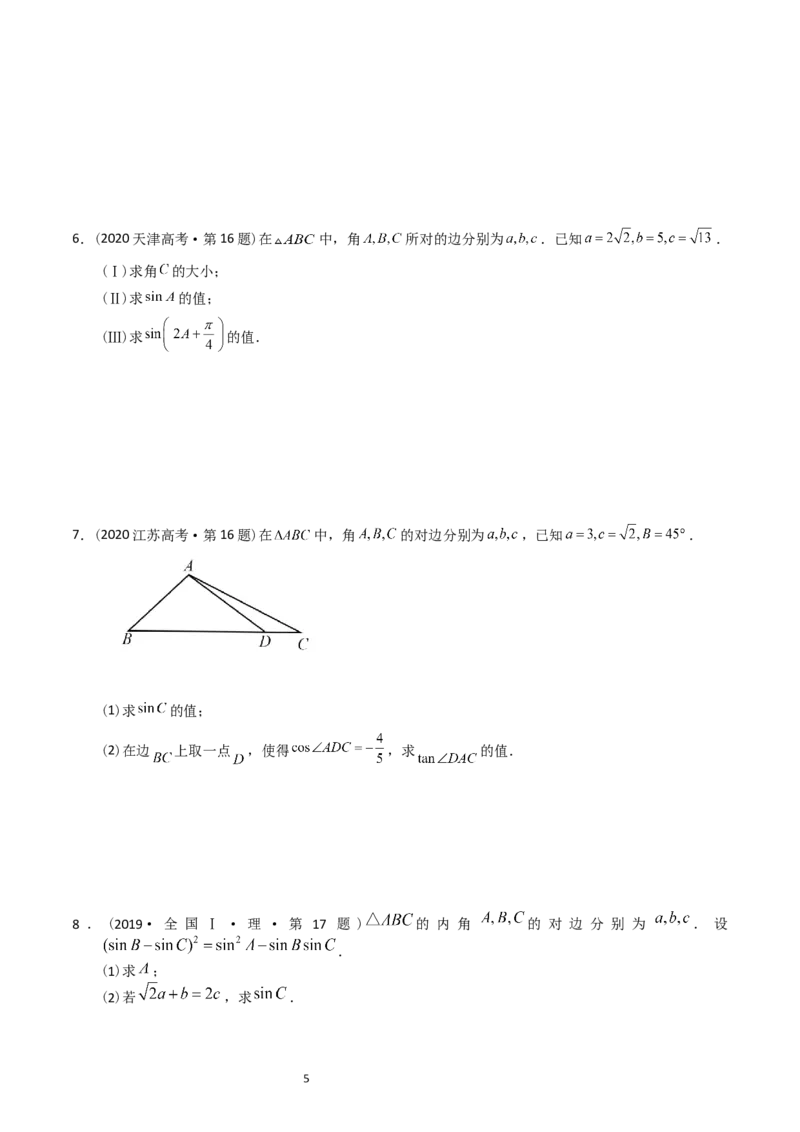
13.(2021年高考全国甲卷理科·第8题)2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为
8848.86(单位:m),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现
有A.B.C三点,且A.B.C在同一水平面上的投影 满足 , .
由C点测得B点的仰角为 , 与 的差为100;由B点测得A点的仰角为 ,则A.C两点到
水平面 的高度差 约为( ) ( )
A.346 B.373 C.446 D.473
二 填空题
1.(2021年高考全国乙卷理科·第15题)记 的内角A,B,C的对边分别为a,b,c,面积为 ,
, ,则 ________.
2.(2021年高考浙江卷·第14题)在 中, ,M是 的中点, ,则
___________, ___________.
3.(2020年高考课标Ⅰ卷理科·第16题)如图,在三棱锥P–ABC的平面展开图中,
AC=1, ,AB⊥AC,AB⊥AD,∠CAE=30°,则
cos∠FCB=______________.
4.(2019·浙江·第14题)在 中, , , ,点 在线段
上.若 ,则 , .
5.(2019·全国Ⅱ·理·第15题) 的内角 , , 的对边分别为 , , .若 , ,
,则 的面积为 .
26.(2023年全国甲卷理科·第16题)在 中, , 的角平分线
交BC于D,则 _________.
三 解答题
1 . (2023 年 天 津 卷 · 第 16 题 ) 在 中 , 角 所 对 的边 分 別 是 . 已 知
.
(1)求 的值;
(2)求 的值;
(3)求 .
2.(2023年新课标全国Ⅰ卷·第17题)已知在 中, .
(1)求 ;
(2)设 ,求 边上的高.
2.(2023年新课标全国Ⅱ卷·第17题)记 的内角 的对边分别为 ,已知 的面积
为 , 为 中点,且 .
(1)若 ,求 ;
(2)若 ,求 .
33.(2021年新高考Ⅰ卷·第19题)记 是内角 , , 的对边分别为 , , .已知 ,点
在边 上, .
(1)证明: ;
(2)若 ,求 .
4.(2020年浙江省高考数学试卷·第18题)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且
.
(I)求角B;
(II)求cosA+cosB+cosC的取值范围.
5.(2022新高考全国I卷·第18题)记 的内角A,B,C的对边分别为a,b,c,已知
.
(1)若 ,求B;
(2)求 的最小值.
46.(2020天津高考·第16题)在 中,角 所对的边分别为 .已知 .
(Ⅰ)求角 的大小;
(Ⅱ)求 的值;
(Ⅲ)求 的值.
7.(2020江苏高考·第16题)在 中,角 的对边分别为 ,已知 .
(1)求 的值;
(2)在边 上取一点 ,使得 ,求 的值.
8 . (2019· 全 国 Ⅰ · 理 · 第 17 题 ) 的 内 角 的 对 边 分 别 为 . 设
.
(1)求 ;
(2)若 ,求 .
59.(2019·江苏·第15题)在 中,角 的对边分别为 .
(1)若 ,求 的值;
(2)若 ,求 的值.
10.(2019·北京·理·第15题)在△ABC中, , , .
(Ⅰ)求 的值;
(Ⅱ)求sin(B–C)的值.
考点 02 三角形中面积周长问题
1.(2023年全国乙卷理科·第18题)在 中,已知 , , .
(1)求 ;
(2)若D为BC上一点,且 ,求 的面积.
62.(2021年新高考全国Ⅱ卷·第18题)在 中,角 、 、 所对的边长分别为 、 、 ,
, ..
(1)若 ,求 的面积;
(2)是否存在正整数 ,使得 为钝角三角形?若存在,求出 的值;若不存在,说明理由.
3.(2020年高考课标Ⅱ卷理科·第17题) 中,sin2A-sin2B-sin2C=sinBsinC.
(1)求A;
(2)若BC=3,求 周长的最大值.
4.(2022高考北京卷·第16题)在 中, .
(1)求 ;
(2)若 ,且 的面积为 ,求 的周长.
75.(2022年浙江省高考数学试题·第18题)在 中,角A,B,C所对的边分别为a,b,c.已知
.
(1)求 的值;
(2)若 ,求 的面积.
6.(2022新高考全国II卷·第18题)记 的内角A,B,C的对边分别为a,b,c,分别以a,b,c为
边长的三个正三角形的面积依次为 ,已知 .
(1)求 面的积;
(2)若 ,求b.
7.(2022年高考全国乙卷数学(理)·第17题)记 的内角 的对边分别为 ,已知
.
8(1)证明: ;
(2)若 ,求 的周长.
考点 03 机构不良试题
1.(2020年新高考全国Ⅰ卷(山东)·第17题)在① ,② ,③ 这三个条件中任选
一个,补充在下面问题中,若问题中的三角形存在,求 的值;若问题中的三角形不存在,说明理由.
问题:是否存在 ,它的内角 的对边分别为 ,且 , ,
________?
注:如果选择多个条件分别解答,按第一个解答计分.
2.(2020年新高考全国卷Ⅱ数学(海南)·第17题)在① ,② ,③ 这三个条件中
任选一个,补充在下面问题中,若问题中 的三角形存在,求 的值;若问题中的三角形不存在,说明
理由.
问题:是否存在 ,它的内角 的对边分别为 ,且 , ,
________?
注:如果选择多个条件分别解答,按第一个解答计分.
3.(2021高考北京·第16题)在 中, , .
9(1)求角B的大小;
(2)再从条件①、条件②、条件③这三个条件中选择一个作为已知,使 存在且唯一确定,求
边上中线的长.
条件①: ;
条件②: 周长为 ;条件③: 的面积为 ;
的
4.(2020北京高考·第17题)在 中, ,再从条件①、条件②这两个条件中选择一个作为
己知,求:
(Ⅰ) 的值:
(Ⅱ) 和 的面积.
条件①: ;
条件②: .
注:如果选择条件①和条件②分别解答,按第一个解答计分.
10