文档内容
五年(2019-2023)年高考真题分项汇编
专题 11 数列
数列作为高考必考题,高考题型一般作为1小1大或者是2小1大模式。主要考点:
考点01 数列概念及通项
考点02 等差等比数列应用
考点03 数列求和
考点04 数列情景类问题
考点05 数列新定义问题
考点06 数列与其他知识点交汇及综合问题
考点 01 数列概念及通项
一 选择题
1.(2021年高考浙江卷·第10题)已知数列 满足 .记数列 的前n项和为
,则 ( )
A. B. C. D.
【答案】A
【解析】因为 ,所以 , .
由
,即
根据累加法可得, ,当且仅当 时取等号,
1,当且仅当 时取等号,
所以 ,即 .
故选A.
二、填空题
1.(2022高考北京卷·第15题) 己知数列 各项均为正数,其前n项和 满足 .
给出下列四个结论:
① 的第2项小于3; ② 为等比数列;
③ 为递减数列; ④ 中存在小于 的项.
其中所有正确结论的序号是__________.
【答案】①③④
【解析】由题意可知, , ,
当 时, ,可得 ;
当 时,由 可得 ,两式作差可得 ,
所以, ,则 ,整理可得 ,
因为 ,解得 ,①对;
假设数列 为等比数列,设其公比为 ,则 ,即 ,
所以, ,可得 ,解得 ,不合乎题意,
故数列 不 是等比数列,②错;
当 时, ,可得 ,所以,数列 为递减数列,③对;
假设对任意 , ,则 ,
的
所以, ,与假设矛盾,假设不成立,④对.
故答案为:①③④.
2考点 02 等差等比数列应用
一 选择题
1.(2020北京高考·第8题)在等差数列 中, , .记 ,则数列
( ).
A.有最大项,有最小项 B.有最大项,无最小项
C.无最大项,有最小项 D.无最大项,无最小项
【答案】B
【解析】由题意可知,等差数列的公差 ,
则其通项公式为: ,
注意到 ,且由 可知 ,
由 可知数列 不存在最小项,
由于 ,
故数列 中的正项只有有限项: , .故数列 中存在最大项,且最大项
为 .故选:B.
2.(2019·全国Ⅰ·理·第9题)记 为等差数列 的前 项和.已知 , ,则 (
)
A. B. C. D.
【答案】A
解析: ,
所以 ,故选A.
3.(2023年天津卷·第6题)已知 为等比数列, 为数列 的前 项和, ,则 的值
为 ( )
A.3 B.18 C.54 D.152
【答案】C
解析:由题意可得:当 时, ,即 , ①
当 时, ,即 , ②
联立①②可得 ,则 .
3故选:C.
2.(2023年新课标全国Ⅱ卷·第8题)记 为等比数列 的前n项和,若 , ,则 (
).
A.120 B.85 C. D.
【答案】C
解析:方法一:设等比数列 的公比为 ,首项为 ,
若 ,则 ,与题意不符,所以 ;
由 , 可得, , ①,
由①可得, ,解得: ,
所以 .
故选:C.
方法二:设等比数列 的公比为 ,
因为 , ,所以 ,否则 ,
从而, 成等比数列,
所以有, ,解得: 或 ,
当 时, ,即为 ,
易知, ,即 ;
当 时, ,
与 矛盾,舍去.故选:C.
4.(2023 年全国甲卷理科·第 5 题)设等比数列 的各项均为正数,前 n 项和 ,若 ,
,则 ( )
A. B. C.15 D.40
【答案】C解析:由题知 ,
即 ,即 ,即 .
4由题知 ,所以 .
所以 .
故选:C.
5.(2022年高考全国乙卷数学(理)·第8题)已知等比数列 的前3项和为168, ,则 (
)
A.14 B.12 C.6 D.3
【答案】D解析:设等比数列 的公比为 ,
若 ,则 ,与题意矛盾,
所以 ,则 ,解得 ,
所以 .故选:D.
6.(2019·全国Ⅲ·理·第5题)已知各项均为正数的等比数列 的前4项和为15,且 ,则
( )
A.16 B.8 C.4 D.2
【答案】C
【解析】设正数的等比数列 的公比为 ,则 ,解得 ,
,故选C.另解:数感好的话由 ,立即会想到数列: ,检验是否
满足 ,可以迅速得出 .
二、填空题
1.(2019·全国Ⅲ·理·第14题) 记 为等差数列{a}的前n项和, ,则 ___________.
n
【 答 案 】 4 . 【 解 析 】 因 , 所 以 , 即 , 所 以
.
【点评】本题主要考查等差数列的性质、基本量的计算.渗透了数学运算素养.使用转化思想得出答案.
2.(2019·江苏·第8题) 已知数列 是等差数列, 是其前n项和.若 ,则
的值是 .
5【答案】16【解析】由 ,得 ,从而 ,即 ,解得
,所以 .
3.(2019·北京·理·第10题) 设等差数列 的前 n项和为 ,若 a=−3,S=−10,则
2 5
a=__________,S 的最小值为__________.
5 n
【答案】 (1) 0; (2) -10.
【解析】等差数列 中, ,得 ,则公差 ,
∴ ,
由等差数列 的性质得 时, ,当 时, 大于0,所以 的最小值为 或 ,
值为 .
3.(2023年全国乙卷理科·第15题) 已知 为等比数列, , ,则 ______.
【答案】
解析:设 的公比为 ,则 ,显然 ,
则 ,即 ,则 ,因为 ,则 ,
则 ,则 ,则 ,
故答案为: .
4.(2019·全国Ⅰ·理·第 14 题) 记 为等比数列 的前 项和.若 , ,则
.
【答案】 解析:由 ,得 ,所以 ,又因为 ,所以 ,
.
5.(2020江苏高考·第11题)设 是公差为 的等差数列, 是公比为 的等比数列.已知数列
的前 项和 ,则 的值是_______.
【答案】
【解析】设等差数列 的公差为 ,等比数列 的公比为 ,根据题意 .
等差数列 的前 项和公式为 ,
等比数列 的前 项和公式为 ,
6依题意 ,即 ,
通过对比系数可知 ,故 .故答案为:
考点 03 数列求和
一 选择题
1.(2020年高考课标Ⅱ卷理科·第6题)数列 中, , ,若
,则 ( )
A.2 B.3 C.4 D.5
【答案】C
解析:在等式 中,令 ,可得 , ,
所以,数列 是以 为首项,以 为公比的等比数列,则 ,
,
,则 ,解得 .
故选:C.
【点睛】本题考查利用等比数列求和求参数的值,解答的关键就是求出数列的通项公式,考查计算能
力,属于中等题.
二、填空题
1.(2020年浙江省高考数学试卷·第11题) 已知数列{a}满足 ,则S=________.
n 3
【答案】10
解析:因为 ,所以 .
即 .
2.(2020年新高考全国卷Ⅱ数学(海南)·第15题) 将数列{2n–1}与{3n–2}的公共项从小到大排列得到数
列{a},则{a}的前n项和为________.
n n
7【答案】
解析:因为数列 是以1为首项,以2为公差的等差数列,
数列 是以1首项,以3为公差的等差数列,
所以这两个数列的公共项所构成的新数列 是以1为首项,以6为公差的等差数列,
所以 的前 项和为 ,
故答案为: .
3.(2019·上海·第8题)已知数列 前n项和为 ,且满足 ,则 ______.
【答案】
【解析】由 得: ( )
【点评】本题主要考查数列求和, 的递推式.
∴ 为等比数列,且 , ,∴ .
三 解答题:
1.(2023年新课标全国Ⅱ卷·第18题) 已知 为等差数列, ,记 , 分别为数
列 , 的前n项和, , .
(1)求 的通项公式;
(2)证明:当 时, .
【答案】(1) ;
(2)证明见解析.
解析:(1)
设等差数列 的公差为 ,而 ,
则 ,
于是 ,解得 , ,
8所以数列 的通项公式是 .
(2)
方法1:由(1)知, , ,
当 为偶数时, ,
,
当 时, ,因此 ,
当 为奇数时, ,
当 时, ,因此 ,
所以当 时, .
方法2:由(1)知, , ,
当 为偶数时,
,
当 时, ,因此 ,
当 为奇数时,若 ,则
,显然 满足上式,因此当 为奇数时, ,
当 时, ,因此 ,
所以当 时, .
2.(2021年新高考Ⅰ卷·第17题) 已知数列 满足 ,
(1)记 ,写出 , ,并求数列 的通项公式;
(2)求 的前20项和.
9【答案】 ; .
【解析】(1)由题设可得
又 , ,故 即 即
所以 为等差数列,故 .
(2)设 的前 项和为 ,则 ,
因为 ,
所以
.
3.(2019·全国Ⅱ·理·第 19 题) 已知数列 和 满足 , , ,
.
证明: 是等比数列, 是等差数列;
求 和 的通项公式.
【答案】 见解析; , .
【官方解析】
由题设得 ,即 .
又因为 ,所以 是首项为 ,公比为 的等比数列.
由题设得 ,即 .
又因为 ,所以 是首项为 ,公差为 的等差数列.
由 知, , .
所以 ,
.
【分析】 可通过题意中的 以及 对两式进行相加和相减即可推导
出数列 是等比数列以及数列 是等差数列;
可通过 中的结果推导出数列 以及数列 的通项公式,然后利用数列 以及
10数列 的通项公式即可得出结果.
【解析】 由题意可知4a 3a b 4,4b 3b a 4,a +b =1,a b 1,
n1 n n n1 n n 1 1 1 1
所以 ,即 ,
4a +4b =3a -b +4+3b - a - 4=2a +2b
n+1 n+1 n n n n n n
1
所以数列a b 是首项为 、公比为 的等比数列,a +b =( 1)n-1,
n n 1 2 n n 2
因为4a - 4b =3a -b +4-(3b - a - 4) =4a - 4b +8,
n+1 n+1 n n n n n n
所以a
n+1
-b
n+1
=a
n
-b
n
+2,数列 a
n
b
n
是首项1、公差为2 的等差数列,a
n
-b
n
=2n-1.
由 可知, , ,
a -b =2n-1
n n
所以 , .
4.(2021年高考全国乙卷理科·第19题) 记 为数列 的前n项和, 为数列 的前n项积,已知
.
(1)证明:数列 是等差数列;
(2)求 的通项公式.
【答案】(1)证明见解析;(2) .
解析:(1)由已知 得 ,且 , ,
取 ,由 得 ,
由于 为数列 的前n项积,
所以 ,
所以 ,
11所以 ,
由于
所以 ,即 ,其中
所以数列 是以 为首项,以 为公差等差数列;
(2)由(1)可得,数列 是以 为首项,以 为公差的等差数列,
,
,
当n=1时, ,
当n≥2时, ,显然对于n=1不成立,
∴ .
5.(2023年新课标全国Ⅰ卷·第20题) 设等差数列 的公差为 ,且 .令 ,记
分别为数列 的前 项和.
(1)若 ,求 的通项公式;
(2)若 为等差数列,且 ,求 .
【答案】(1)
(2)
解析:(1) , ,解得 ,
,
12又 ,
,
即 ,解得 或 (舍去),
.
(2) 为等差数列,
,即 ,
,即 ,解得 或 ,
, ,
又 ,由等差数列性质知, ,即 ,
,即 ,解得 或 (舍去)
当 时, ,解得 ,与 矛盾,无解;
当 时, ,解得 .
综上, .
6.(2022年高考全国甲卷数学(理)·第17题) 记 为数列 的前n项和.已知 .
(1)证明: 是等差数列;
(2)若 成等比数列,求 的最小值.
【答案】(1)证明见解析; (2) .
【解析】(1)解:因为 ,即 ①,
当 时, ②,
① ②得, ,
即 ,
即 ,所以 , 且 ,
13所以 是以 为公差的等差数列.
(2)解:由(1)可得 , , ,
又 , , 成等比数列,所以 ,
即 ,解得 ,
所以 ,所以 ,
所以,当 或 时 .
7.(2021年新高考全国Ⅱ卷·第17题) 记 是公差不为0的等差数列 的前n项和,若 .
(1)求数列 的通项公式 ;
(2)求使 成立的n的最小值.
【答案】【解析】(1)由等差数列的性质可得: ,则: ,
设等差数列的公差为 ,从而有: ,
,
从而: ,由于公差不为零,故: ,数列的通项公式为: .
(2)由数列的通项公式可得: ,则: ,
则不等式 即: ,整理可得: ,解得: 或 ,又 为正整数,
故 的最小值为 .
8(2023年全国乙卷)1.记 为等差数列 的前 项和,已知 .
(1)求 的通项公式;
(2)求数列 的前 项和 .
【答案】(1)
(2)
【分析】(1)根据题意列式求解 ,进而可得结果;
(2)先求 ,讨论 的符号去绝对值,结合 运算求解.
【详解】(1)设等差数列的公差为 ,
14由题意可得 ,即 ,解得 ,
所以 ,
(2)因为 ,
令 ,解得 ,且 ,
当 时,则 ,可得 ;
当 时,则 ,可得
;
综上所述: .
9.(2020年新高考全国Ⅰ卷(山东)·第18题) 已知公比大于 的等比数列 满足 .
(1)求 的通项公式;
(2)记 为 在区间 中的项的个数,求数列 的前 项和 .
【答案】(1) ;(2) .
解析:(1)由于数列 是公比大于 的等比数列,设首项为 ,公比为 ,依题意有 ,
解得解得 ,或 (舍),
所以 ,所以数列 的通项公式为 .
(2)由于 ,所以
对应的区间为: ,则 ;
对应的区间分别为: ,则 ,即有 个 ;
对应的区间分别为: ,则 ,即有 个 ;
对应的区间分别为: ,则 ,即有 个 ;
对应的区间分别为: ,则 ,即有 个 ;
对应的区间分别为: ,则 ,即有 个 ;
15对应的区间分别为: ,则 ,即有 个
.
所以 .
10.(2020年新高考全国卷Ⅱ数学(海南)·第18题) 已知公比大于 的等比数列 满足
.
(1)求 的通项公式;
(2)求 .
【答案】(1) ;(2)
解析:(1) 设等比数列 的公比为q(q>1),则 ,
整理可得: ,
,
数列的通项公式为: .
(2)由于: ,故:
.
11 .(2023年全国甲卷理科·第17题) 设 为数列 的前n项和,已知 .
(1)求 的通项公式;
(2)求数列 的前n项和 .
【答案】(1)
(2)
解析:(1)因为 ,
16当 时, ,即 ;
当 时, ,即 ,
当 时, ,所以 ,
化简得: ,当 时, ,即 ,
当 时都满足上式,所以 .
(2)因为 ,所以 ,
,
两式相减得,
,
,即 , .
12 .(2020天津高考·第19题) 已知 为等差数列, 为等比数列,
.
(Ⅰ)求 和 的通项公式;
(Ⅱ)记 的前 项和为 ,求证: ;
(Ⅲ)对任意的正整数 ,设 求数列 的前 项和.
【答案】(Ⅰ) , ;(Ⅱ)证明见解析;(Ⅲ) .
【解析】(Ⅰ)设等差数列 的公差为 ,等比数列 的公比为 .由 , ,可得 .
从而 的通项公式为 .由 ,又 ,可得 ,解得 ,
从而 的通项公式为 .
17(Ⅱ)证明:由(Ⅰ)可得 ,
故 , ,
从而 ,所以 .
(Ⅲ)当 为奇数时, ,
当 为偶数时, ,
对任意的正整数 ,有 ,
和 ①
由①得 ②
由①②得 ,
由于 ,
从而得: .
因此, .所以,数列 的前 项和为 .
考点 04 数列情景类题目
一、选择题
1.(2020年高考课标Ⅱ卷理科·第0题)北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中
心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块,
下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块,已知每层环数相同,且下层
比中层多729块,则三层共有扇面形石板(不含天心石) ( )
18( )
A.3699块 B.3474块 C.3402块 D.3339块
【答案】C
解析:设第n环天石心块数为 ,第一层共有n环,
则 是以9为首项,9为公差的等差数列, ,
设 为 的前n项和,则第一层、第二层、第三层的块数分
别为 ,因为下层比中层多729块,
所以 ,
即
即 ,解得 ,
所以 .
故选:C
【点晴】本题主要考查等差数列前n项和有关的计算问题,考查学生数学运算能力,是一道容易题.
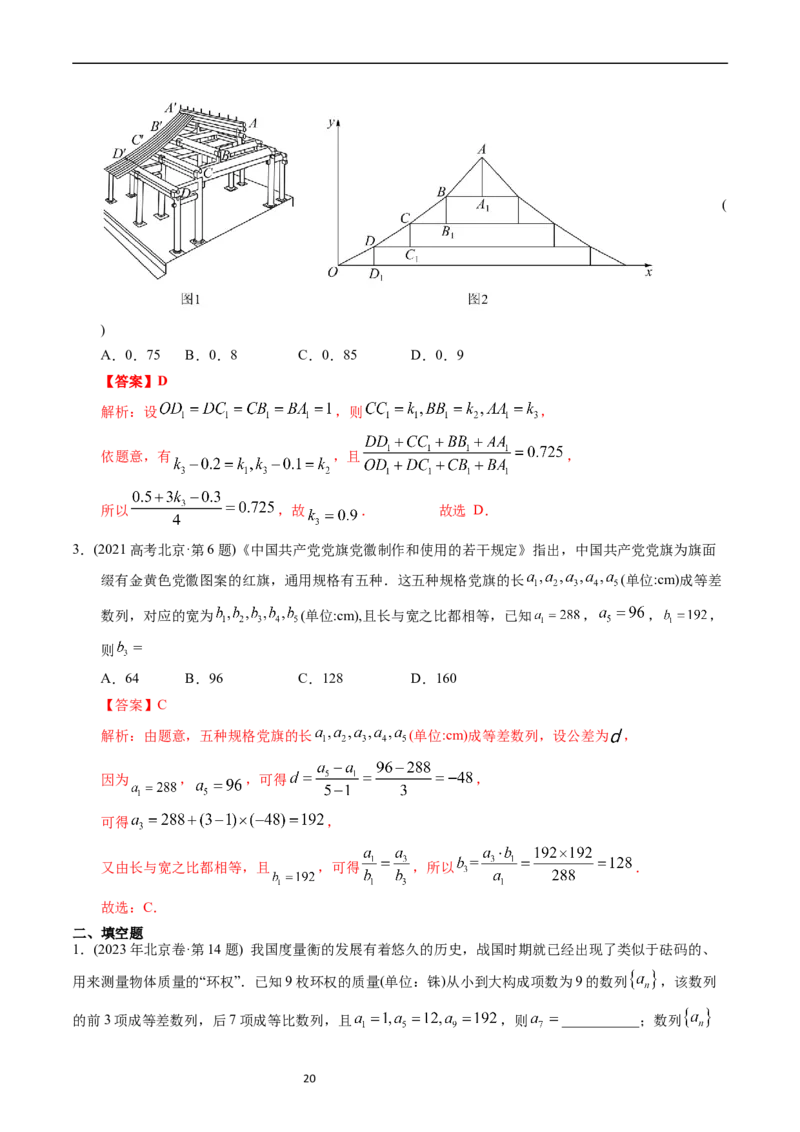
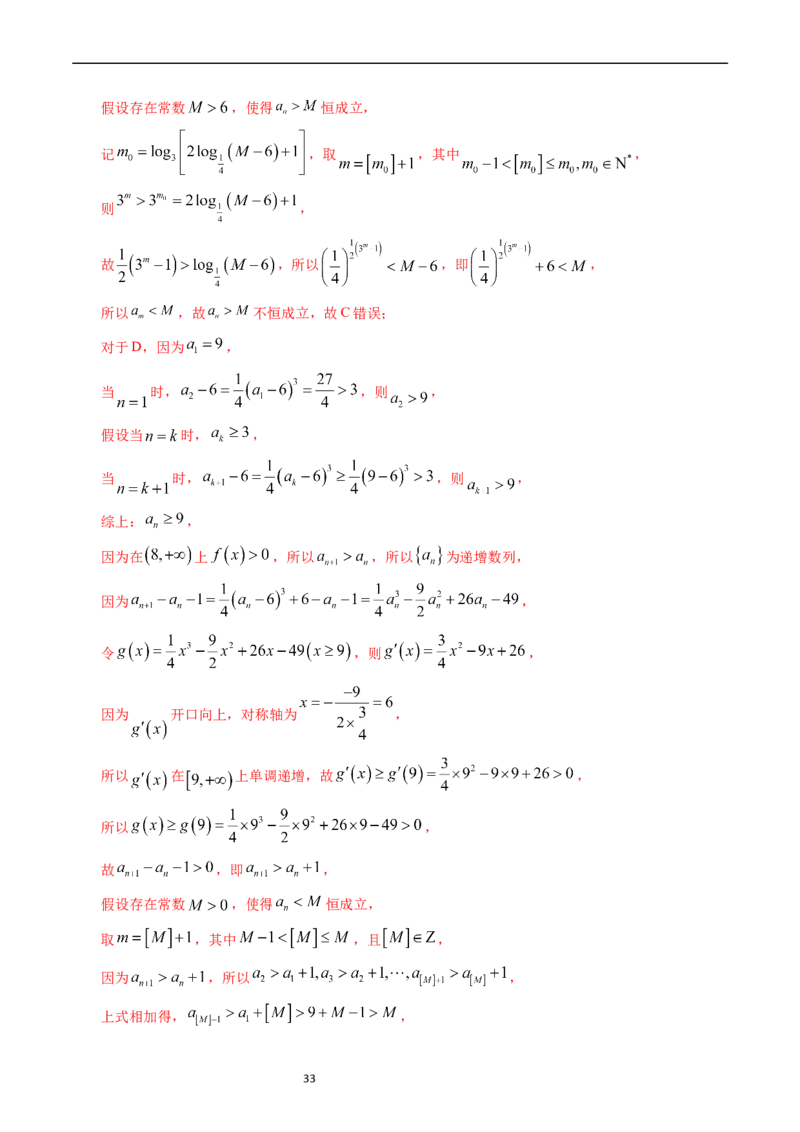
2.(2022新高考全国II卷·第3题)图1是中国古代建筑中的举架结构, 是桁,相邻桁的
水平距离称为步,垂直距离称为举,图2是某古代建筑屋顶截面的示意图.其中
是举, 是相等的步,相邻桁的举步之比分别为
.已知 成公差为0.1的等差数列,且直线 的
斜率为0.725,则 ( )
19(
)
A.0.75 B.0.8 C.0.85 D.0.9
【答案】D
解析:设 ,则 ,
依题意,有 ,且 ,
所以 ,故 . 故选 D.
3.(2021高考北京·第6题)《中国共产党党旗党徽制作和使用的若干规定》指出,中国共产党党旗为旗面
缀有金黄色党徽图案的红旗,通用规格有五种.这五种规格党旗的长 (单位:cm)成等差
数列,对应的宽为 (单位:cm),且长与宽之比都相等,已知 , , ,
则
A.64 B.96 C.128 D.160
【答案】C
解析:由题意,五种规格党旗的长 (单位:cm)成等差数列,设公差为 ,
因为 , ,可得 ,
可得 ,
又由长与宽之比都相等,且 ,可得 ,所以 .
故选:C.
二、填空题
1.(2023年北京卷·第14题) 我国度量衡的发展有着悠久的历史,战国时期就已经出现了类似于砝码的、
用来测量物体质量的“环权”.已知9枚环权的质量(单位:铢)从小到大构成项数为9的数列 ,该数列
的前3项成等差数列,后7项成等比数列,且 ,则 ___________;数列
20所有项的和为____________.
【答案】①. 48 ②. 384
解析:方法一:设前3项的公差为 ,后7项公比为 ,
则 ,且 ,可得 ,
则 ,即 ,可得 ,
空1:可得 ,
空2:
方法二:空1:因为 为等比数列,则 ,
且 ,所以 ;
又因为 ,则 ;
空2:设后7项公比为 ,则 ,解得 ,
可得 ,
所以 .
故答案为:48;384.
2.(2021年新高考Ⅰ卷·第16题)某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把
纸对折,规格为 的长方形纸,对折1次共可以得到 , 两种规格
的图形,它们的面积之和 ,对折2次共可以得到 , ,
三种规格的图形,它们的面积之和 ,以此类推,则对折4次共可以得到不同规格图形的种
数为______;如果对折 次,那么 ______ .
【答案】 5
【解析】(1)对折 次可得到如下规格: , , , ,
,共 种;
21(2)由题意可得 , , , , , ,
设 ,
则 ,
两式作差得
,
因此, ,故答案为 ; .
考点 05 数列新定义问题
1 .(2023年北京卷·第21题) 已知数列 的项数均为m ,且
的前n项和分别为 ,并规定 .对于 ,定义
,其中, 表示数集M中最大的数.
(1)若 ,求 的值;
(2)若 ,且 ,求 ;
(3)证明:存在 ,满足 使得 .
【答案】(1) , , ,
(2)
(3)证明见详解
解析:(1)由题意可知: ,
当 时,则 ,故 ;
当 时,则 ,故 ;
当 时,则 故 ;
当 时,则 ,故 ;
综上所述: , , , .
22(2)由题意可知: ,且 ,
因为 ,则 ,当且仅当 时,等号成立,
所以 ,
又因为 ,则 ,即 ,
可得 ,
反证:假设满足 的最小正整数为 ,
当 时,则 ;当 时,则 ,
则 ,
又因为 ,则 ,
假设不成立,故 ,
即数列 是以首项为1,公差为1的等差数列,所以 .
(3)
(ⅰ)若 ,构建 ,由题意可得: ,且 为整数,
反证,假设存在正整数 ,使得 ,
则 ,可得 ,
.
这与 相矛盾,故对任意 ,均有
①若存在正整数 ,使得 ,即 ,
可取 ,使得 ;
②若不存在正整数 ,使得 ,
因为 ,且 ,
所以必存在 ,使得 ,
即 ,可得 ,
可取 ,使得 ;
(ⅱ)若 ,构建 ,由题意可得: ,且 为整数,
反证,假设存在正整数 ,使得 ,
则 ,可得 ,
这与 相矛盾,故对任意 ,均有 .
23①若存在正整数 ,使得 ,即 ,
可取 ,使得 ;
②若不存在正整数 ,使得 ,
因为 ,且 ,
所以必存在 ,使得 ,
即 ,可得 ,
可取 ,使得 ;
综上所述:存在 使得 .
2.(2019·上海·第21题) 数列 有 项, ,对任意 ,存在 ,
若 与前 项中某一项相等,则称 具有性质 .
(1)若 ,求 可能的值;
(2)若 不为等差数列,求证: 中存在满足性质 ;
(3)若 中恰有三项具有性质 ,这三项和为 ,使用 表示 .
【答案】(1)3,5,7;(2);(3)
【解析】(1)由题意,
①若 具有性质 ,则
②若 具有性质 而 不具有性质 ,则 即
;
③若 不具有性质 ,则必有 即 ;
此时若 具有性质 ,则 ;若 不具有性质 ,则
综上所述, 可能的值为3、5、7
(2)假设 中不存在满足性质 的项,即对任意 均有 ;
下面数学归纳法证明, 是等差数列;
①当 时, 成立;
②设当 且 时, ;
则当 时,因为 不具有性质 ,故
而又存在 故, ,即 ;
24综上所述,当 中不存在满足性质 的项时, 时等差数列成立;
故其逆否命题:当 不是等差数列时, 中存在满足性质 的项成立.
(3)由题意,不妨设这三项为 ,其中 ;且
故数列 为等差数列; 为等差数列;
为等差数列, 为等差数列;
若存在 或 或 的情况
则去掉相应的 、 、 每组等差
数列的公差均为 ;
且 、 、
故当数列去掉 这三项后,构成首项为 ,公差为 ,项数97项的等差数列;
故这97项的和 ;
故这100个数的和
3.(2019·江苏·第20题) 定义首项为1且公比为正数的等比数列为“ -数列”.
(1)已知等比数列 满足: ,求证:数列 为“ -数列”;
(2)已知数列{b}满足: ,其中 为数列 的前 项和.
n
①求数列 的通项公式;
②设 为正整数,若存在“ -数列” ,对任意正整数 ,当 时,都有 成
立,求 的最大值.
【答案】见解析
【解析】(1)设等比数列 的公比为 ,所以 ,
由 ,得 ,解得 .
因此数列 为“M—数列”.
(2)①因为 ,所以
由 得 ,则
由 ,得
25当 时,由 ,得
整理得 .
所以数列 是首项和公差均为1的等差数列.
因此,数列 的通项公式为 .
②由①知, , .
因为数列 为“ –数列”,设公比为 ,所以 , .
因为 ,所以 ,其中 .
当 时,有 ;
当 时,有 .
设f(x)= ,则 .
令 ,得 .列表如下:
x (1,e) e (e,+∞)
+ 0 –
f(x) 极大值
因为 ,所以 .
取 ,当 时, ,即 ,
经检验知 也成立.
因此所求 的最大值不小于5.
若 ,分别取 ,得 ,且 ,从而 ,且 ,
所以 不存在.因此所求 的最大值小于6.
4.(2019·北京·理·第20题) 已知数列 ,从中选取第 项、第 项、…、第 项( < <…< ),若
,则称新数列 为 的长度为m的递增子列.规定:数列 的任意
一项都是 的长度为1的递增子列.
(Ⅰ)写出数列1,8,3,7,5,6,9的一个长度为4的递增子列;
(Ⅱ)已知数列 的长度为p的递增子列的末项的最小值为 ,长度为q的递增子列的末项的最小值为
.若p<q,求证: < ;
26(Ⅲ)设无穷数列{a}的各项均为正整数,且任意两项均不相等.若 的长度为 的递增子列末项的最小
n
值为 ,且长度为 末项为 的递增子列恰有 个( ),求数列 的通项公式.
【答案】【解析】(Ⅰ)满足题意的一个长度为4的递增子列为:1,3,5,6.
(Ⅱ)对于每一个长度为 的递增子列 ,都能从其中找到若干个长度为 的递增子列
,此时 ,
设所有长度为 的子列的末项分别为: ,
所有长度为 的子列的末项分别为: ,则 ,
注意到长度为 的子列可能无法进一步找到长度为 的子列,故 ,
据此可得: .
(Ⅲ)满足题意的一个数列的通项公式可以是 ,
下面说明此数列满足题意.
很明显数列为无穷数列,且各项均为正整数,任意两项均不相等.
长度为 的递增子列末项的最小值为 ,
下面用数学归纳法证明长度为 末项为 的递增子列恰有 个 :
当 时命题显然成立,
假设当 时命题成立,即长度为 末项为 的递增子列恰有 个,
则当 时,对于 时得到的每一个子列 ,
可构造: 和 两个满足题意的递增
子列,则长度为k+1末项为2k+1的递增子列恰有 个,
综上可得,数列 是一个满足题意的数列的通项公式.
注:当 时,所有满足题意的数列为: ,
当 时,数列 对应的两个递增子列为: 和 .
考点 06 数列与其他知识点交汇及综合问题
27一、选择题
1.(2023年北京卷·第10题)已知数列 满足 ,则 (
)
A.当 时, 为递减数列,且存在常数 ,使得 恒成立
B.当 时, 为递增数列,且存在常数 ,使得 恒成立
C.当 时, 为递减数列,且存在常数 ,使得 恒成立
D.当 时, 为递增数列,且存在常数 ,使得 恒成立
【答案】B
解析:法1:因为 ,故 ,
对于A ,若 ,可用数学归纳法证明: 即 ,
证明:当 时, ,此时不等关系 成立;
设当 时, 成立,
则 ,故 成立,
由数学归纳法可得 成立.
而 ,
, ,故 ,故 ,
故 为减数列,注意
故 ,结合 ,
所以 ,故 ,故 ,
若存在常数 ,使得 恒成立,则 ,
故 ,故 ,故 恒成立仅对部分 成立,
故A不成立.
28对于B,若 可用数学归纳法证明: 即 ,
证明:当 时, ,此时不等关系 成立;
设当 时, 成立,
则 ,故 成立即
由数学归纳法可得 成立.
而 ,
, ,故 ,故 ,故 为增数列,
若 ,则 恒成立,故B正确.
对于C,当 时, 可用数学归纳法证明: 即 ,
证明:当 时, ,此时不等关系成立;
设当 时, 成立,
则 ,故 成立即
由数学归纳法可得 成立.
而 ,故 ,故 为减数列,
又 ,结合 可得: ,所
以 ,
若 ,若存在常数 ,使得 恒成立,
则 恒成立,故 , 的个数有限,矛盾,故C错误.
对于D,当 时, 可用数学归纳法证明: 即 ,
证明:当 时, ,此时不等关系成立;
设当 时, 成立,
29则 ,故 成立
由数学归纳法可得 成立.
而 ,故 ,故 为增数列,
又 ,结合 可得:
,所以 ,
若存在常数 ,使得 恒成立,则 ,
故 ,故 ,这与n的个数有限矛盾,故D错误.
故选:B.
法2:因为 ,
令 ,则 ,
令 ,得 或 ;
令 ,得 ;
所以 在 和 上单调递增,在 上单调递减,
令 ,则 ,即 ,解得 或 或
,
注意到 , ,
所以结合 的单调性可知在 和 上 ,在 和 上 ,
对于A,因为 ,则 ,
30当 时, , ,则 ,
假设当 时, ,
当 时, ,则 ,
综上: ,即 ,
因为在 上 ,所以 ,则 为递减数列,
因为 ,
令 ,则 ,
因为 开口向上,对称轴为 ,
所以 在 上单调递减,故 ,
所以 在 上单调递增,故 ,
故 ,即 ,
假设存 在常数 ,使得 恒成立,
取 ,其中 ,且 ,
因为 ,所以 ,
上式相加得, ,
则 ,与 恒成立矛盾,故A错误;
对于B,因为 ,
当 时, , ,
假设当 时, ,
当 时,因为 ,所以 ,则 ,
所以 ,
31又当 时, ,即 ,
假设当 时, ,
当 时,因为 ,所以 ,则 ,
所以 ,
综上: ,
因为在 上 ,所以 ,所以 为递增数列,
此时,取 ,满足题意,故B正确;
对于C,因为 ,则 ,
注意到当 时, , ,
猜想当 时, ,
当 与 时, 与 满足 ,
假设当 时, ,
当 时,所以 ,
综上: ,
易知 ,则 ,故 ,
所以 ,
因为在 上 ,所以 ,则 为递减数列,
32假设存在常数 ,使得 恒成立,
记 ,取 ,其中 ,
则 ,
故 ,所以 ,即 ,
所以 ,故 不恒成立,故C错误;
对于D,因为 ,
当 时, ,则 ,
假设当 时, ,
当 时, ,则 ,
综上: ,
因为在 上 ,所以 ,所以 为递增数列,
因为 ,
令 ,则 ,
因为 开口向上,对称轴为 ,
所以 在 上单调递增,故 ,
所以 ,
故 ,即 ,
假设存在常数 ,使得 恒成立,
取 ,其中 ,且 ,
因为 ,所以 ,
上式相加得, ,
33则 ,与 恒成立矛盾,故D错误.
故选:B.
2.(2020年浙江省高考数学试卷·第7题)已知等差数列{a}的前n项和S,公差d≠0, .记b=S,
n n 1 2
b =S –S , ,下列等式不可能成立的是 ( )
n+1 n+2 2n
A.2a=a+a B.2b=b+b C. D.
4 2 6 4 2 6
【答案】D
解析:对于A,因为数列 为等差数列,所以根据等差数列的下标和性质,由 可得,
,A正确;
对于B,由题意可知, , ,
∴ , , , .
∴ , .
根据等差数列的下标和性质,由 可得
,B正确;
对于C, ,
当 时, ,C正确;
对于D, ,
,
.
当 时, ,∴ 即 ;
当 时, ,∴ 即 ,所以 ,D不正确.
.
故选:D
3.(2022高考北京卷·第6题)设 是公差不为0的无穷等差数列,则“ 为递增数列”是“存在正整数
,当 时, ”的 ( )
A.充分而不必要条件 B.必要而不充分条件
.
C充分必要条件D.既不充分也不必要条件
【答案】C
34【解析】设等差数列 的公差为 ,则 ,记 为不超过 的最大整数.
若 为单调递增数列,则 ,
若 ,则当 时, ;若 ,则 ,
由 可得 ,取 ,则当 时, ,
所以,“ 是递增数列” “存在正整数 ,当 时, ”;
若存在正整数 ,当 时, ,取 且 , ,
假设 ,令 可得 ,且 ,
当 时, ,与题设矛盾,假设不成立,则 ,即数列 是递增数列.
所以,“ 是递增数列” “存在正整数 ,当 时, ”.
所以,“ 是递增数列”是“存在正整数 ,当 时, ”的充分必要条件.
故选,C.
4.(2020年高考课标Ⅱ卷理科·第11题)0-1周期序列在通信技术中有着重要应用.若序列 满足
,且存在正整数 ,使得 成立,则称其为0-1周期序列,并称满
足 的最小正整数 为这个序列的周期.对于周期为 的0-1序列 ,
是描述其性质的重要指标,下列周期为5的0-1序列中,满足
的序列是 ( )
A. B. C. D.
【答案】C
解析:由 知,序列 的周期为m,由已知, ,
对于选项A,
,不满足;
35对于选项B,
,不满足;
对于选项D,
,不满足;
故选:C
【点晴】本题考查数列的新定义问题,涉及到周期数列,考查学生对新定义的理解能力以及数学运算
能力,是一道中档题.
5.(2023年全国乙卷理科·第10题)已知等差数列 的公差为 ,集合 ,若
,则 ( )
A.-1 B. C.0 D.
【答案】B
解析:依题意,等差数列 中, ,
显然函数 的周期为 3,而 ,即 最多 3 个不同取值,又
,
则在 中, 或 ,
于是有 ,即有 ,解得 ,
所以 , .
故选:B
二 解答题
1.(2023年天津卷·第19题) 已知 是等差数列, .
(1)求 的通项公式和 .
(2)已知 为等比数列,对于任意 ,若 ,则 ,
(Ⅰ)当 时,求证: ;
(Ⅱ)求 的通项公式及其前 项和.
36【答案】(1) , ;
(2)(Ⅰ)证明见解析;(Ⅱ) ,前 项和为 .
解析:(1)由题意可得 ,解得 ,
则数列 的通项公式为 ,
求和得
.
(2)(Ⅰ)由题意可知,当 时, ,
取 ,则 ,即 ,
当 时, ,
取 ,此时 ,
据此可得 ,
综上可得: .
(Ⅱ)由(Ⅰ)可知: ,
据此猜测 ,
否则,若数列的公比 ,则 ,
注意到 ,则 不恒成立,即 不恒成立,
此时无法保证 ,
若数列的公比 ,则 ,
注意到 ,则 不恒成立,即 不恒成立,
此时无法保证 ,
综上,数列的公比为 ,则数列的通项公式为 ,
37其前 项和为: .
2.(2022新高考全国I卷·第17题) 记 为数列 的前n项和,已知 是公差为 的等差数
列.
(1)求 的通项公式;
(2)证明: .
【答案】(1)
(2)见解析
解析:(1)∵ ,∴ ,∴ ,又∵ 是公差为 的等差数列,
∴ ,∴ ,∴当 时, ,
∴ ,整理得: ,
即 ,∴
,
显然对于 也成立,
∴ 的通项公式 ;
(2)
∴
3.(2014高考数学课标1理科·第17题) 已知数列 {a } 的前n项和为S ,a =1,a 0,a a S 1,其
n n 1 n n n1 n
中为常数.
(1)证明: a - a =l;
n+2 n
38{a }
(2)是否存在,使得 为等差数列?并说明理由.
n
【答案】【解析】(1)由题设
a a =lS -1
,
a a =lS -1
,两式相减
n n+1 n n+1 n+2 n+1
a (a - a ) =la ,由于a � 0,所以a - a =l.
n+1 n+2 n n+1 n n+2 n
(2) 由题设 a =1 , aa =lS -1 ,可得 a =l -1 ,由(1)知 a =l+1
1 1 2 1 2 1 3
假设 {a } 为等差数列,则 a ,a ,a 成等差数列,∴ a +a =2a ,解得l =4;
n 1 2 3 1 3 2
证明l =4时, {a } 为等差数列:由 a - a =4 知
n n+2 n
数列奇数项构成的数列 {a } 是首项为1,公差为4的等差数列a =4m-3
2m-1 2m-1
n+1
令 则m= ,∴
n=2m-1, 2 a =2n-1 (n=2m-1)
n
数列偶数项构成的数列 {a } 是首项为3,公差为4的等差数列a =4m-1
2m 2m
n
令 则m= ,∴
n=2m, 2 a =2n-1 (n=2m)
n
∴ a =2n-1 (n� N*), a - a =2
n n+1 n
因此,存在存在l =4,使得 {a } 为等差数列.
n
4.(2020年浙江省高考数学试卷·第20题) 已知数列{a},{b},{c}中,
n n n
.
(Ⅰ)若数列{b}为等比数列,且公比 ,且 ,求q与a 的通项公式;
n n
(Ⅱ)若数列{b}为等差数列,且公差 ,证明: .
n
【答案】(I) ;(II)证明见解析.
解析:(I)依题意 ,而 ,即 ,由于 ,所以解得 ,所
以 .
所以 ,故 ,所以数列 是首项为 ,公比为 的等比数列,所以
.
所以 ( ).
所以
39(II)依题意设 ,由于 ,
所以 ,
故
.
所以
.
由于 ,所以 ,所以 .
即 , .
5 (2023年新高考Ⅱ卷)2.甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,
若末命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为0.6,乙每次投篮的命中率
均为0.8.由抽签确定第1次投篮的人选,第1次投篮的人是甲、乙的概率各为0.5.
(1)求第2次投篮的人是乙的概率;
(2)求第 次投篮的人是甲的概率;
(3)已知:若随机变量 服从两点分布,且 ,则 .
记前 次(即从第1次到第 次投篮)中甲投篮的次数为 ,求 .
【答案】(1)
(2)
(3)
【分析】(1)根据全概率公式即可求出;
(2)设 ,由题意可得 ,根据数列知识,构造等比数列即可解出;
40(3)先求出两点分布的期望,再根据题中的结论以及等比数列的求和公式即可求出.
【详解】(1)记“第 次投篮的人是甲”为事件 ,“第 次投篮的人是乙”为事件 ,
所以,
.
(2)设 ,依题可知, ,则
,
即 ,
构造等比数列 ,
设 ,解得 ,则 ,
又 ,所以 是首项为 ,公比为 的等比数列,
即 .
(3)因为 , ,
所以当 时, ,
故 .
【点睛】本题第一问直接考查全概率公式的应用,后两问的解题关键是根据题意找到递推式,然后根据数
列的基本知识求解.
6.(2022高考北京卷·第21题) 已知 为有穷整数数列.给定正整数m,若对任意的
,在Q中存在 ,使得 ,则称Q为
连续可表数列.
(1)判断 是否为 连续可表数列?是否为 连续可表数列?说明理由;
(2)若 为 连续可表数列,求证:k的最小值为4;
(3)若 为 连续可表数列,且 ,求证: .
【答案】【解析】(1) , , , , ,所以 是 连续可表数列;
41易知,不存在 使得 ,所以 不是 连续可表数列.
(2)若 ,设为 ,则至多 ,6个数字,没有 个,矛盾;
当 时,数列 ,满足 , , , , , ,
, , .
(3) ,若 最多有 种,若 ,最多有 种,所以最多有 种,
若 ,则 至多可表 个数,矛盾,
从而若 ,则 , 至多可表 个数,
而 ,所以其中有负的,从而 可表1~20及那个负数(恰 21个),这表明
中仅一个负的,没有0,且这个负的在 中绝对值最小,同时 中没有两数相同,设那个负数
为 ,
则所有数之和 , ,
,再考虑排序,排序中不能有和相同,否则不足 个,
(仅一种方式),
与2相邻,
若 不在两端,则 形式,
若 ,则 (有2种结果相同,方式矛盾),
, 同理 ,故 在一端,不妨为 形式,
若 ,则 (有2种结果相同,矛盾), 同理不行,
,则 (有2种结果相同,矛盾),从而 ,
由于 ,由表法唯一知3,4不相邻,、
故只能 ,①或 ,②
这2种情形,
对①: ,矛盾,
对②: ,也矛盾,综上
7.(2021年高考浙江卷·第20题) 已知数列 前n项和为 , ,且 .
的
(1)求数列 的通项;
42(2)设数列 满足 ,记 的前n项和为 ,若 对任意 恒成立,求 的
范围.
【答案】(1) ;(2) .
【解析】(1)当 时, , ,
当 时,由 ①,得 ②,① ②得
,又 是首项为 ,公比为 的等比数列,
;
(2)由 ,得 ,
所以 ,
,
两式相减得
,
所以 ,由 得 恒成立,
即 恒成立,
时不等式恒成立;
时, ,得 ;
时, ,得 ;
所以 .
8.(2022新高考全国II卷·第17题) 已知 为等差数列, 是公比为2的等比数列,且
43.
(1)证明: ;
(2)求集合 中元素个数.
【答案】(1)证明见解析;
(2) .
解析:(1)设数列 的公差为 ,所以, ,即可解得, ,所以
原命题得证.
(2)由(1)知, ,所以 ,即 ,亦即
,解得 ,所以满足等式的解 ,故集合
中的元素个数为
9.(2022年浙江省高考数学试题·第20题) 已知等差数列 的首项 ,公差 .记 的前n
项和为 .
(1)若 ,求 ;
(2)若对于每个 ,存在实数 ,使 成等比数列,求d的取值范围.
【答案】【解析】(1)因为 ,
所以 ,
所以 ,又 ,
所以 ,
所以 ,
所以 ,
(2)因为 , , 成等比数列,
所以 ,
,
44,
由已知方程 的判别式大于等于0,
所以 ,
所以 对于任意的 恒成立,
所以 对于任意的 恒成立,
当 时, ,
当 时,由 ,可得
当 时, ,
又
所以
10.(2021年高考全国甲卷理科·第18题) 已知数列 的各项均为正数,记 为 的前n项和,从下
面①②③中选取两个作为条件,证明另外一个成立.
①数列 是等差数列:②数列 是等差数列;③ .
注:若选择不同的组合分别解答,则按第一个解答计分.
【答案】答案见解析
解析:选①②作条件证明③:
设 ,则 ,
当 时, ;
当 时, ;
因为 也是等差数列,所以 ,解得 ;
所以 ,所以 .
选①③作条件证明②:
因为 , 是等差数列,
所以公差 ,
所以 ,即 ,
45因为 ,
所以 是等差数列.
选②③作条件证明①:
设 ,则 ,
当 时, ;
当 时, ;
因为 ,所以 ,解得 或 ;
当 时, ,当 时, 满足等差数列的定义,此时 为等差
数列;
当 时, , 不合题意,舍去.
综上可知 为等差数列.
【点睛】这类题型在解答题中较为罕见,求解的关键是牢牢抓住已知条件,结合相关公式,逐步推演,等
差数列的证明通常采用定义法或者等差中项法.
46