文档内容
专题 21 立体几何大题综合
考点 十年考情(2015-2024) 命题趋势
2024·全国新Ⅰ卷、2024·全国甲卷、2024·北京卷、2024·天津卷、
2023·全国新Ⅰ卷、2023·全国甲卷、2023·全国乙卷、2023·天津
卷、2022·全国新Ⅱ卷、2022·全国甲卷、2022·天津卷、2022·北京
空间中的平
卷
行关系和垂
2021·天津卷、2020·北京卷、2020·江苏卷、2019·江苏卷、
考点1 空间中的平 直关系依然
2019·天津卷、2019·天津卷、2019·全国卷、2019·全国卷、
行关系(第一问) 是立体几何
2018·江苏卷2017·天津卷、2017·浙江卷、2017·全国卷
(10年10考) 大题第一问
2017·全国卷、2017·江苏卷、2016·四川卷、2016·江苏卷、
的 命 题 热
2016·天津卷、2016·全国卷、2016·山东卷、2016·全国卷、
点,要熟练
2015·江苏卷、2015·天津卷、2015·天津卷、2015·四川卷
掌握
2015·山东卷、2015·山东卷、2015·安徽卷
2015·福建卷、2015·北京卷
空间中的距
2024·全国新Ⅱ卷、2023·全国新Ⅱ卷、2023·全国甲卷、2023·北京 离 及 表 面
卷、2022·全国甲卷、2022·全国乙卷、2022·浙江卷、2021·全国新 积、体积的
Ⅰ卷、2021·全国新Ⅱ卷、2021·全国甲卷、2021·全国乙卷、2021· 计算同样是
浙江卷 命题热点,
2020·海南卷、2020·天津卷、2020·浙江卷、2020·山东卷、 异面直线所
2020·全国卷、2020·全国卷、2020·全国卷、2020·全国卷、 成角、线面
2020·全国卷、2019·江苏卷、2019·北京卷、2019·北京卷 角 、 二 面
考点2 空间中的垂
角、及其最
2019·全国卷、2019·全国卷、2019·天津卷、2019·浙江卷、
直关系(第一问) 值范围等内
2019·全国卷、2019·全国卷、2018·江苏卷、2018·北京卷、
(10年10考) 容也是高频
2018·北京卷、2018·全国卷、2018·浙江卷、2018·全国卷
考点,同时
2018·全国卷、2018·全国卷、2018·全国卷、2018·天津卷、
也需掌握方
2017·山东卷、2017·全国卷、2017·天津卷、2017·全国卷、
程思想的应
2017·全国卷、2017·北京卷、2017·江苏卷、2016·浙江卷
用
2016·北京卷、2016·全国卷、2016·北京卷、2016·山东卷、
2016·浙江卷、2016·天津卷、2016·全国卷、2016·全国卷、
2015·广东卷、2015·江苏卷、2015·重庆卷、2015·重庆卷2015·浙江卷、2015·浙江卷、2015·全国卷、2015·全国卷、
2015全国卷、2015·天津卷、2015·陕西卷、2015·湖南卷、
2015·湖南卷、2015·湖北卷、2015·福建卷、2015·北京卷
2015·北京卷
考点3 求空间中的
线段长度、点面距 2024·全国甲卷、2024·天津卷、2023·全国甲卷、2022·全国新Ⅰ
的值及最值或范围 卷、2021·全国乙卷、2019·全国卷、2018·全国卷
(10年6考)
2024·上海卷、2023·全国乙卷、2022·全国甲卷、2022·全国乙卷、
2021·全国新Ⅰ卷、2021·全国甲卷、2021·全国乙卷、2020·全国
考点4 求空间中的 卷、2020·全国卷、2019·全国卷、2019·全国卷、2018·全国卷
体积、表面积的值 2017·上海卷、2017·全国卷、2017·北京卷、2017·全国卷、
及最值或范围 2016·江苏卷、2016·全国卷、2016·上海卷、2016·上海卷、
(10年10考) 2016·全国卷、2016·全国卷、2015·重庆卷、2015·全国卷
2015·湖南卷、2015·湖南卷、2015·湖北卷
2015·福建卷、2015·北京卷
考点5 异面直线所
2018·天津卷、2017·天津卷、2016·上海卷、2015·广东卷、
成角及最值或范围
2015·全国卷、2015·上海卷、2015·山东卷
(10年4考)
2024·天津卷、2024·上海卷、2023·全国甲卷、2022·全国甲卷、
2022·全国乙卷、2022·浙江卷、2022·天津卷、2021·浙江卷、
2020·海南卷、2020·天津卷、2020·北京卷、2020·浙江卷
考点6 求线面角及 2020·山东卷、2020·全国卷、2019·天津卷、2019·浙江卷、
最值或范围 2018·江苏卷、2018·浙江卷、2018·全国卷、2018·天津卷、
(10年10考) 2017·上海卷、2017·天津卷、2017·浙江卷、2017·北京卷
2016·浙江卷、2016·天津卷、2016·全国卷、2016·北京卷、
2016·天津卷、2015·广东卷、2015·浙江卷、2015·天津卷、
2015·上海卷、2015·全国卷
2024·全国新Ⅱ卷、2024·全国甲卷、2024·北京卷、2024·天津卷、
2023·全国新Ⅱ卷、2023·全国乙卷、2023·北京卷、2023·天津卷、
2022·全国新Ⅰ卷、2022·全国新Ⅱ卷、2022·天津卷、2021·全国新
考点7 求二面角及
Ⅱ卷
最值或范围
2021·全国甲卷、2021·全国乙卷、2021·天津卷、2020·天津卷、
(10年10考)
2020·江苏卷、2020·全国卷、2020·全国卷、2019·北京卷、
2019·全国卷、2019·全国卷、2019·全国卷、2018·北京卷
2018·全国卷、2017·山东卷、2017·全国卷、2016·天津卷、2016·山东卷、2016·浙江卷、2016·全国卷、2016·全国卷、
2015·广东卷、2015·重庆卷、2015·浙江卷、2015·四川卷
2015·陕西卷、2015·山东卷、2015·安徽卷
2015·福建卷、2015·北京卷
考点8 已知异面直
线所成角、线面 2024·全国新Ⅰ卷、2023·全国新Ⅰ卷、2021·全国新Ⅰ卷、2021·北
角、二面角求值或 京卷、2017·天津卷、2017·全国卷、2015·天津卷、2015·湖南卷、
范围(方程思想) 2015·湖南卷、2015·湖北卷
(10年5考)
考点01 空间中的平行关系(第一问)
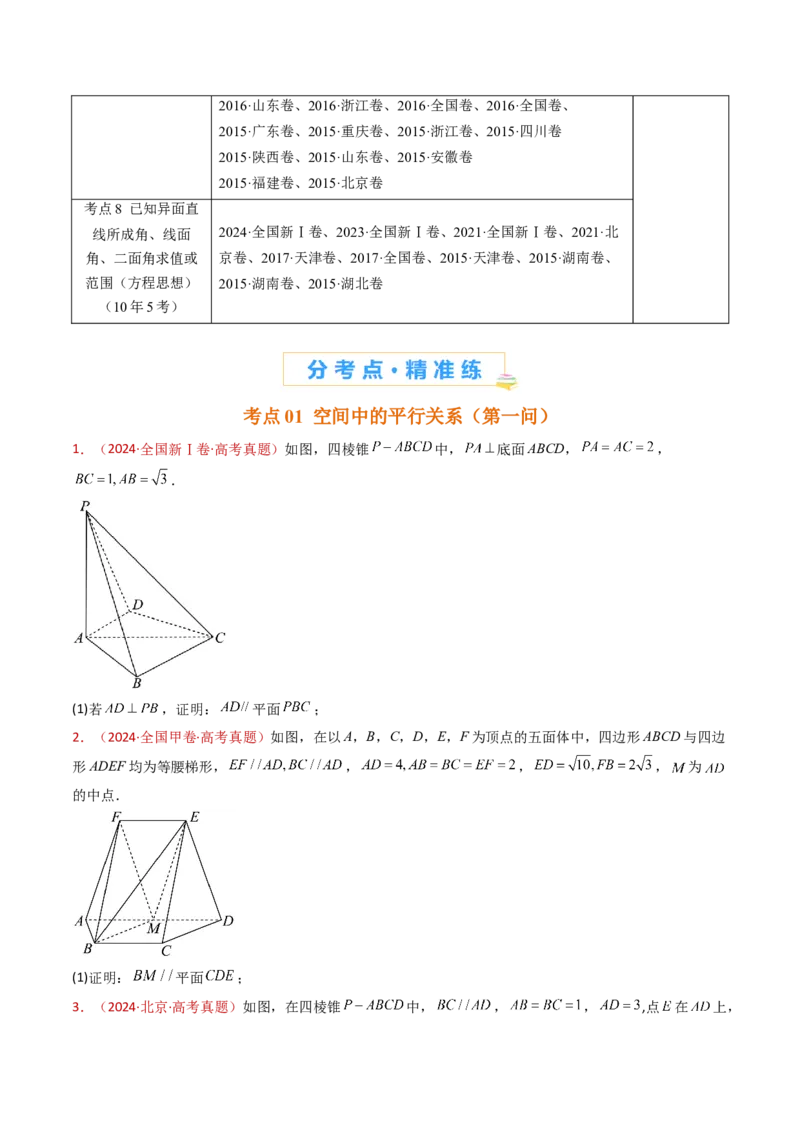
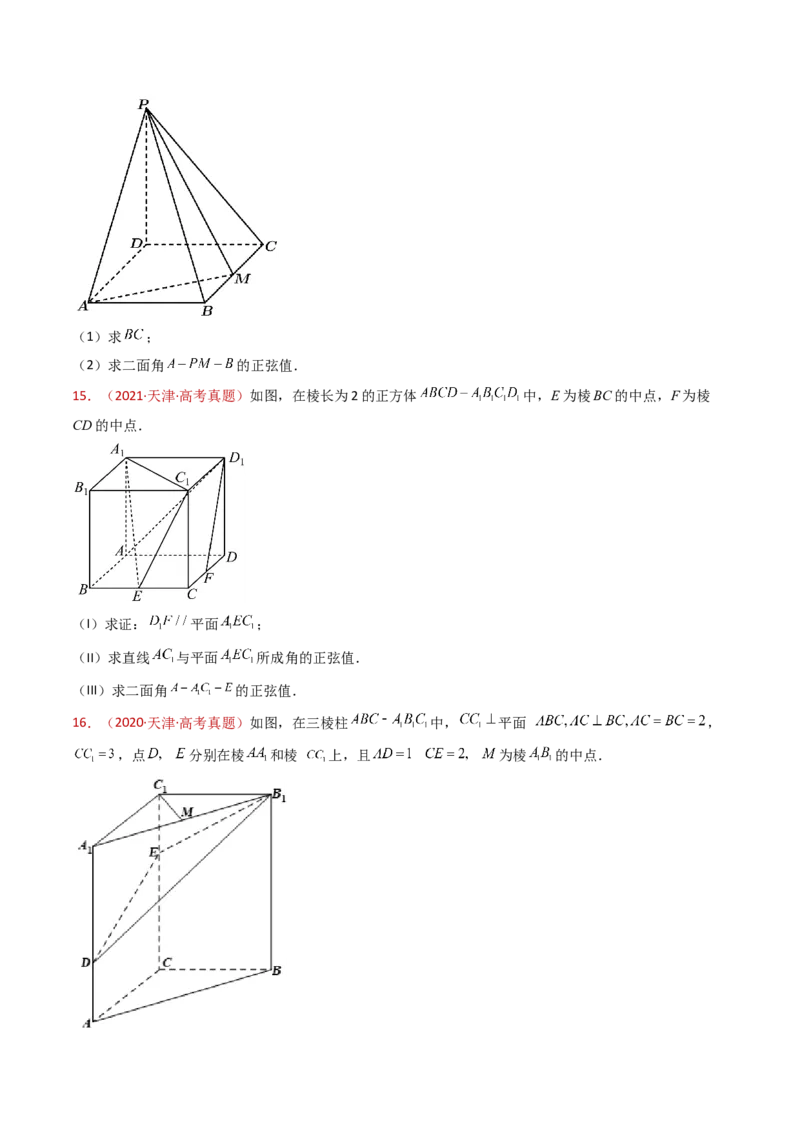
1.(2024·全国新Ⅰ卷·高考真题)如图,四棱锥 中, 底面ABCD, ,
.
(1)若 ,证明: 平面 ;
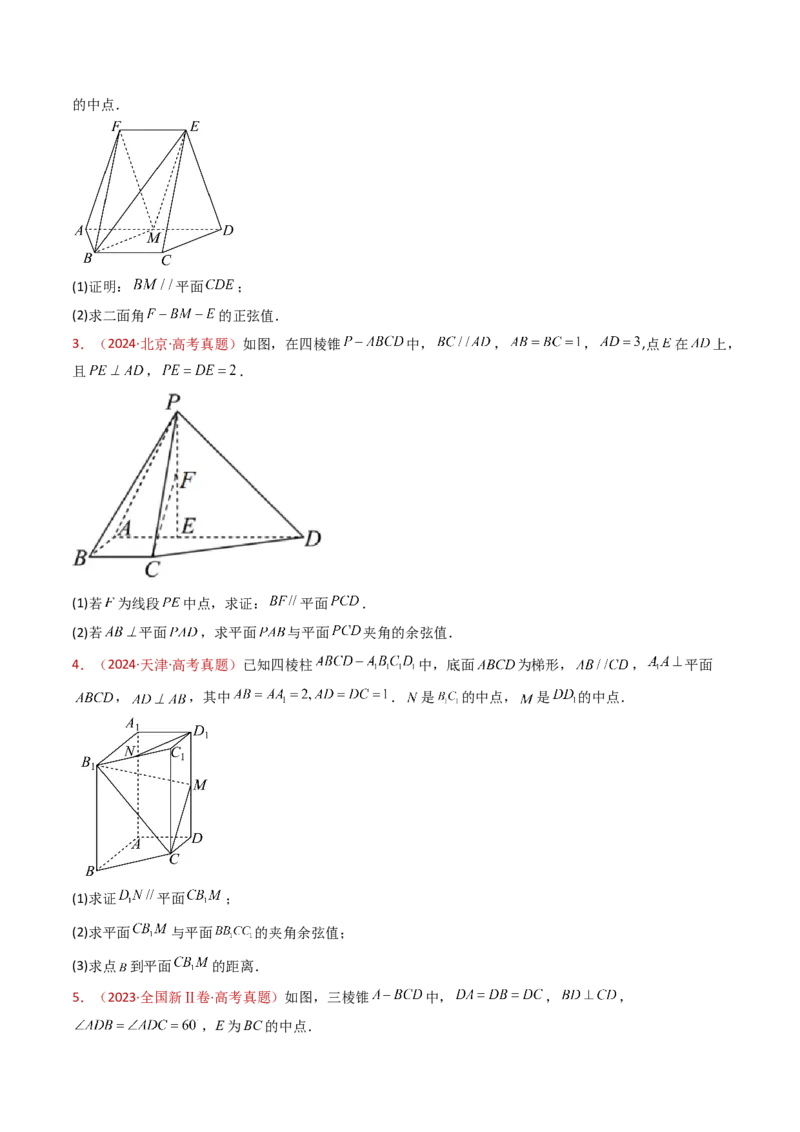
2.(2024·全国甲卷·高考真题)如图,在以A,B,C,D,E,F为顶点的五面体中,四边形ABCD与四边
形ADEF均为等腰梯形, , , , 为
的中点.
(1)证明: 平面 ;
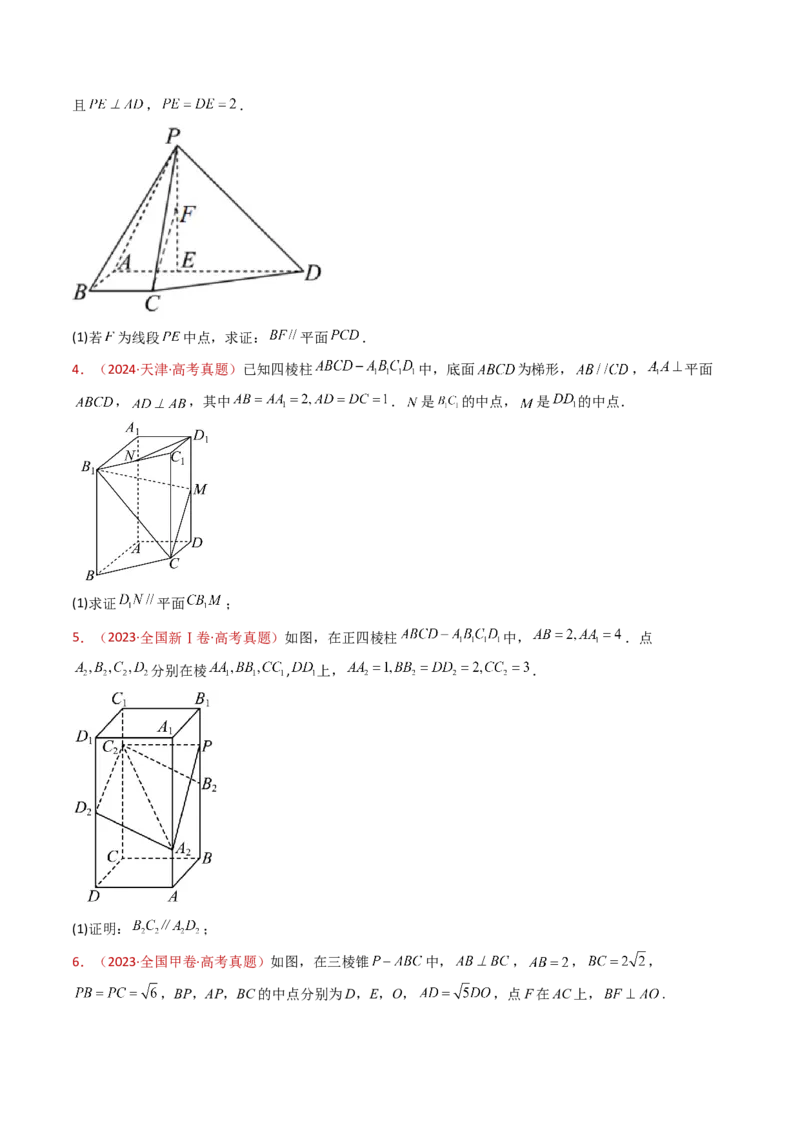
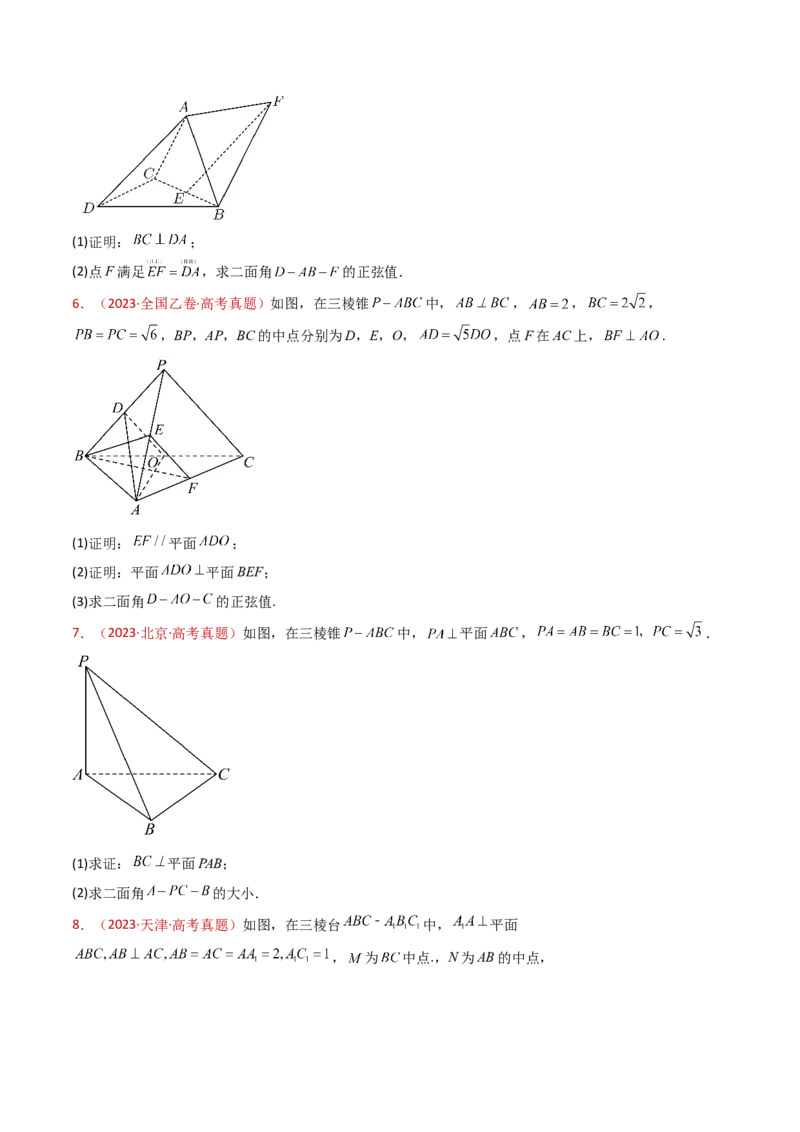
3.(2024·北京·高考真题)如图,在四棱锥 中, , , ,点 在 上,且 , .
(1)若 为线段 中点,求证: 平面 .
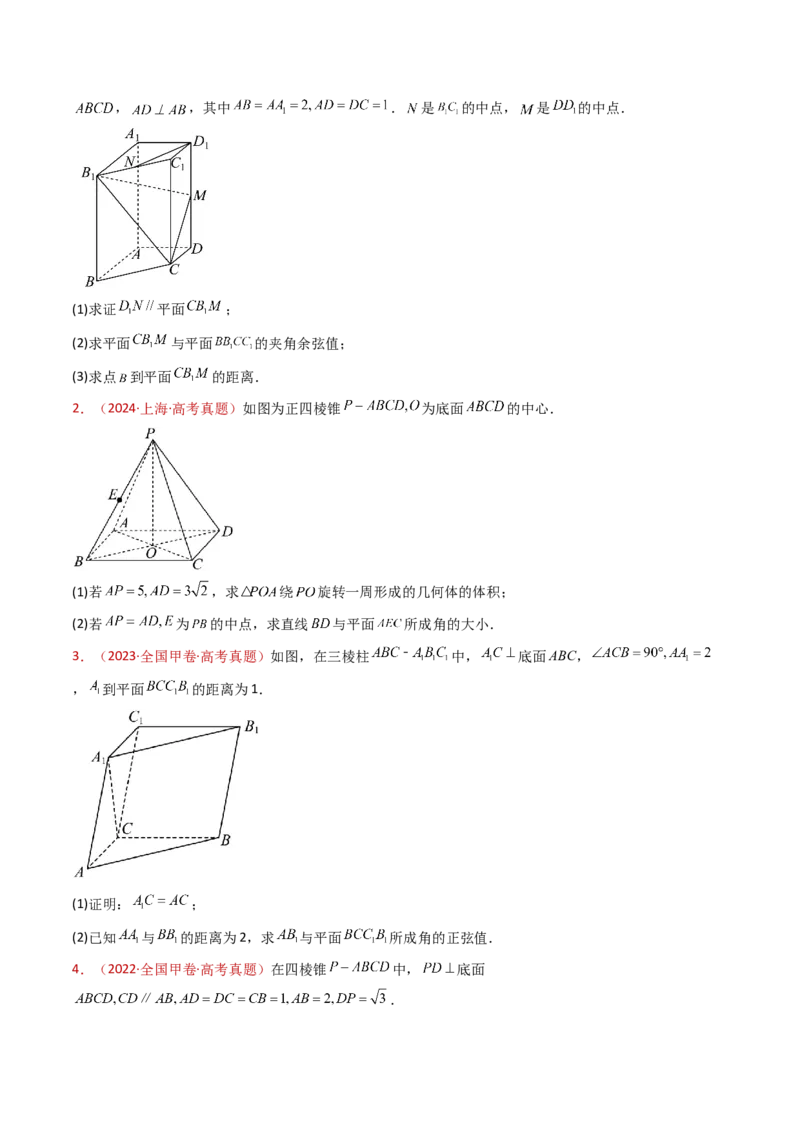
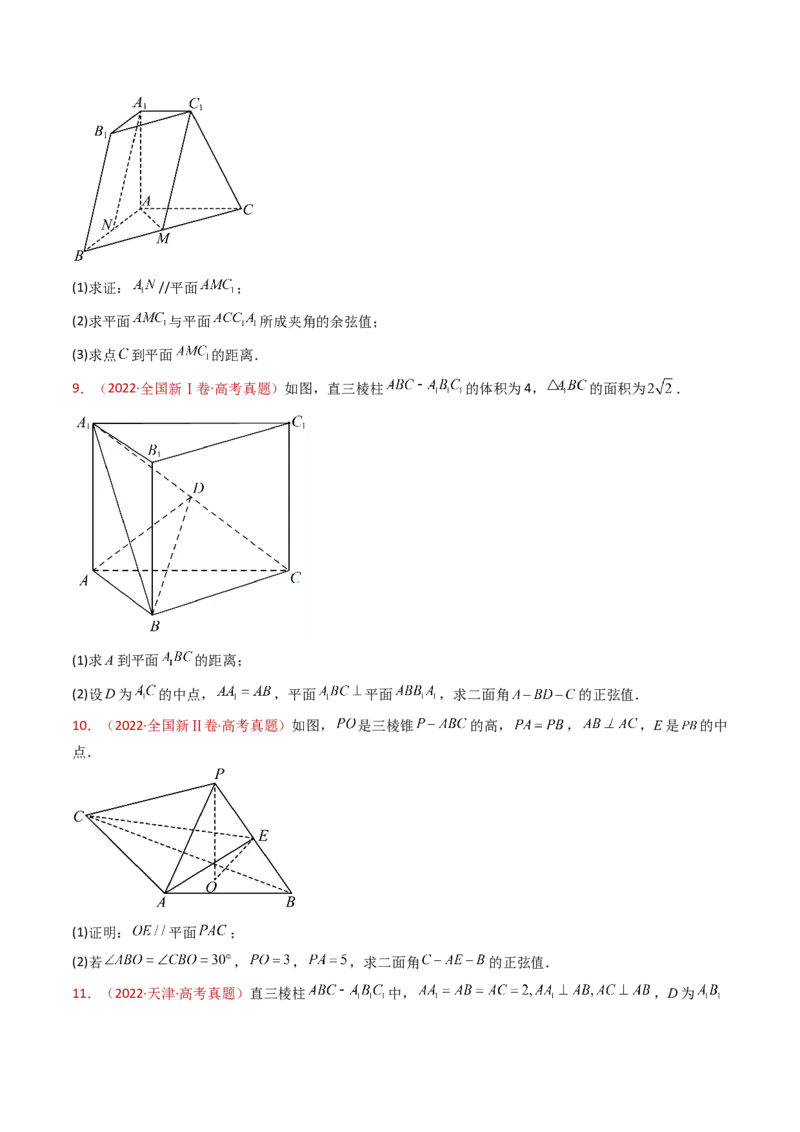
4.(2024·天津·高考真题)已知四棱柱 中,底面 为梯形, , 平面
, ,其中 . 是 的中点, 是 的中点.
(1)求证 平面 ;
5.(2023·全国新Ⅰ卷·高考真题)如图,在正四棱柱 中, .点
分别在棱 , 上, .
(1)证明: ;
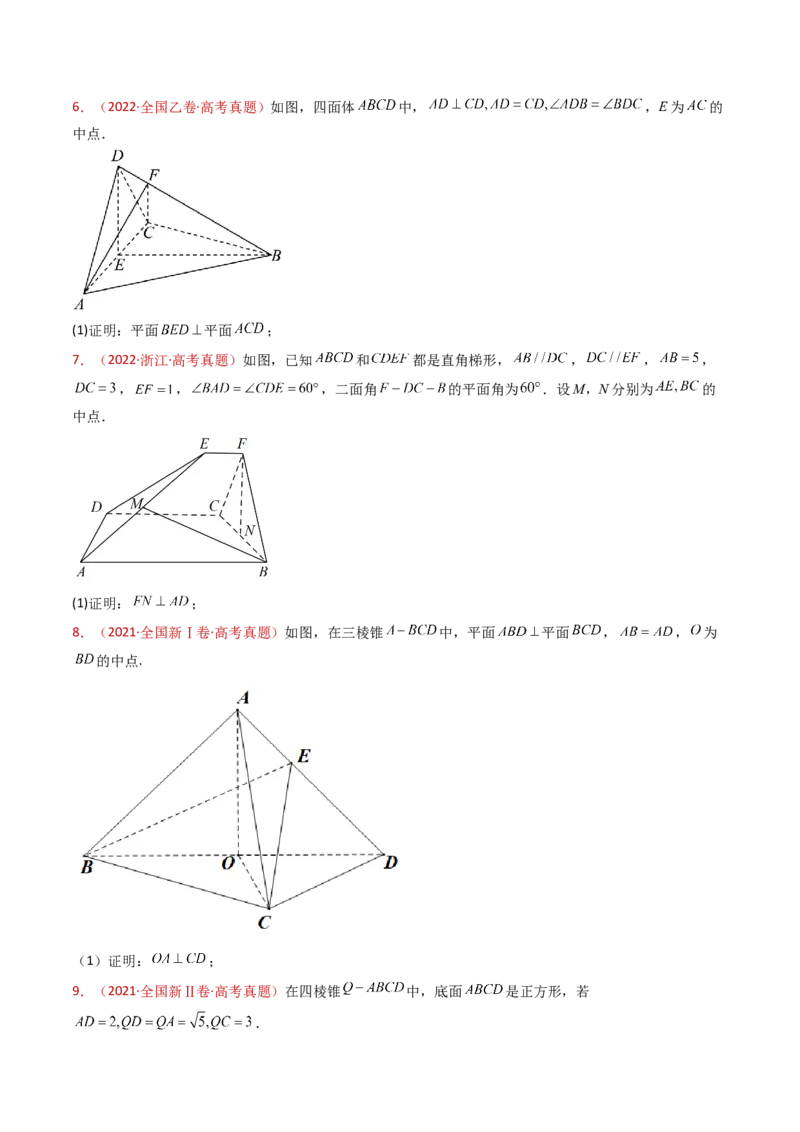
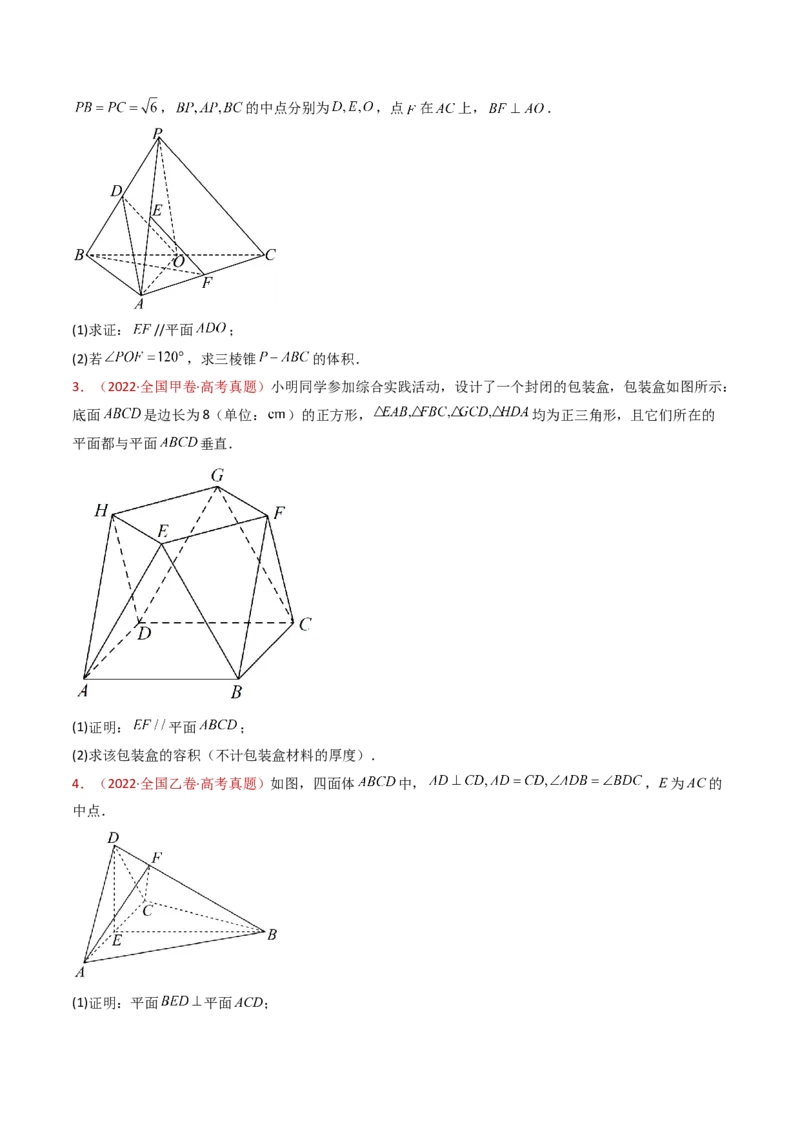
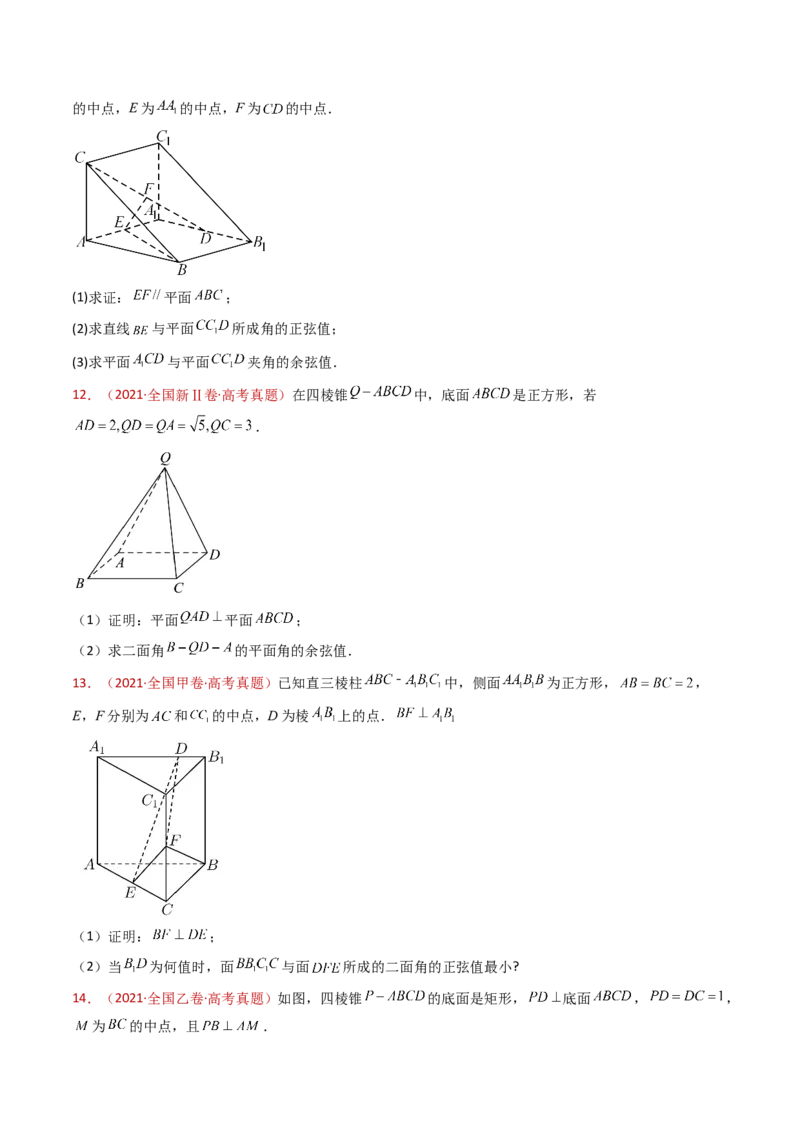
6.(2023·全国甲卷·高考真题)如图,在三棱锥 中, , , ,
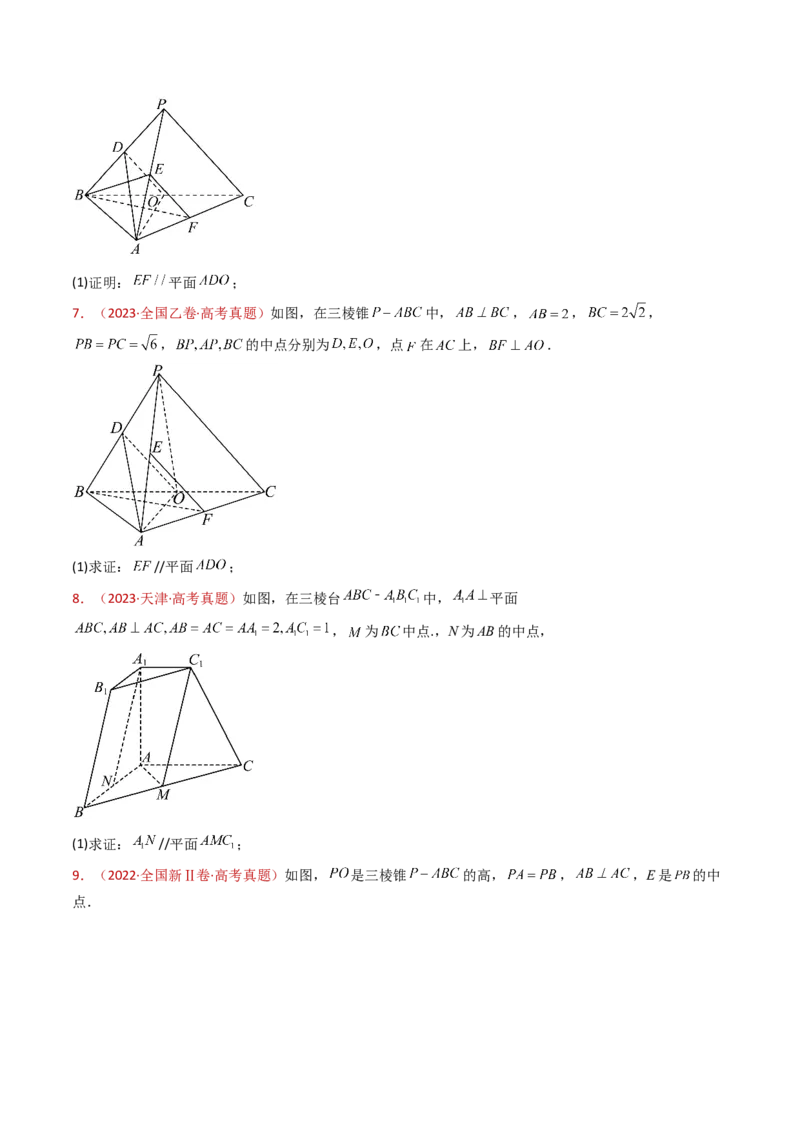
,BP,AP,BC的中点分别为D,E,O, ,点F在AC上, .(1)证明: 平面 ;
7.(2023·全国乙卷·高考真题)如图,在三棱锥 中, , , ,
, 的中点分别为 ,点 在 上, .
(1)求证: //平面 ;
8.(2023·天津·高考真题)如图,在三棱台 中, 平面
, 为 中点.,N为AB的中点,
(1)求证: //平面 ;
9.(2022·全国新Ⅱ卷·高考真题)如图, 是三棱锥 的高, , ,E是 的中
点.(1)证明: 平面 ;
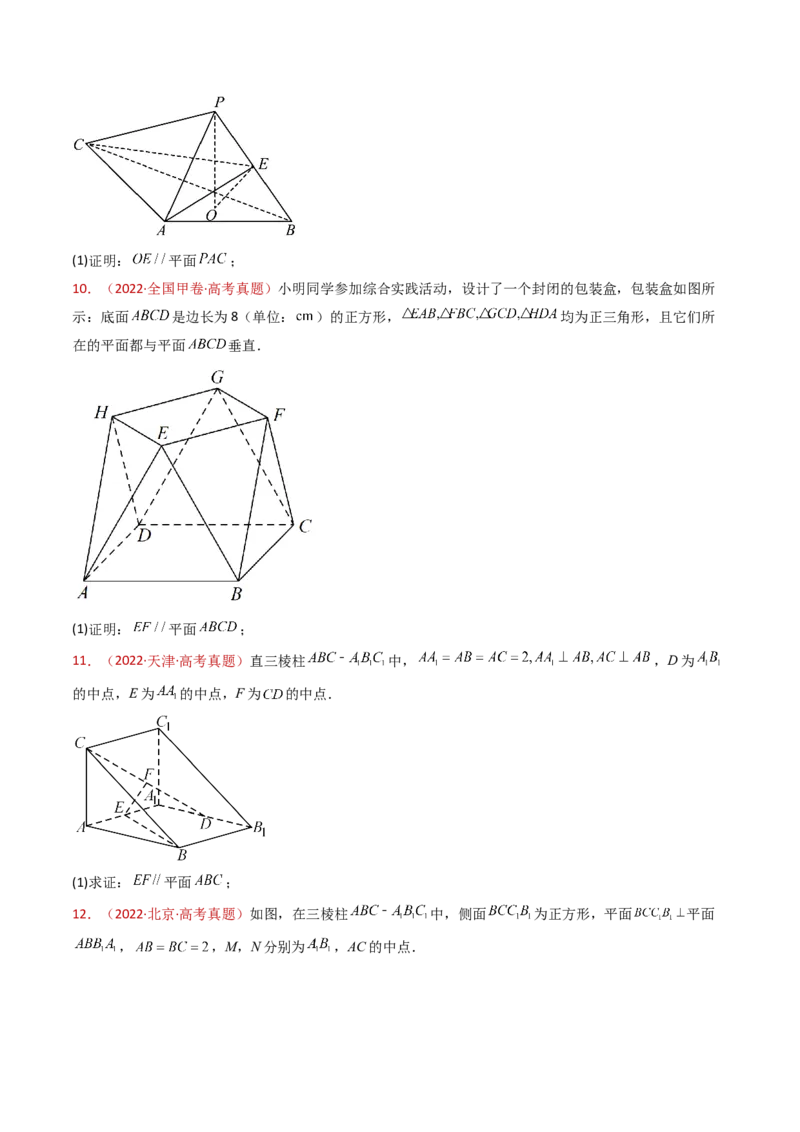
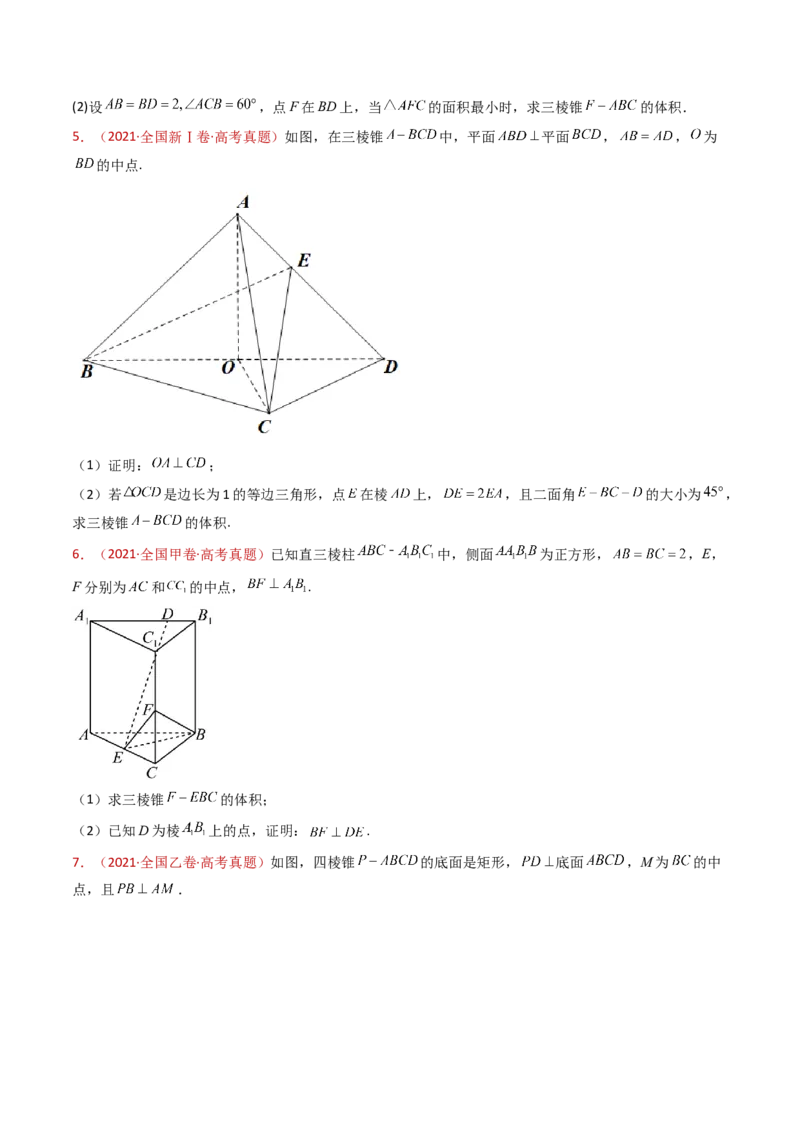
10.(2022·全国甲卷·高考真题)小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所
示:底面 是边长为8(单位: )的正方形, 均为正三角形,且它们所
在的平面都与平面 垂直.
(1)证明: 平面 ;
11.(2022·天津·高考真题)直三棱柱 中, ,D为
的中点,E为 的中点,F为 的中点.
(1)求证: 平面 ;
12.(2022·北京·高考真题)如图,在三棱柱 中,侧面 为正方形,平面 平面
, ,M,N分别为 ,AC的中点.(1)求证: 平面 ;
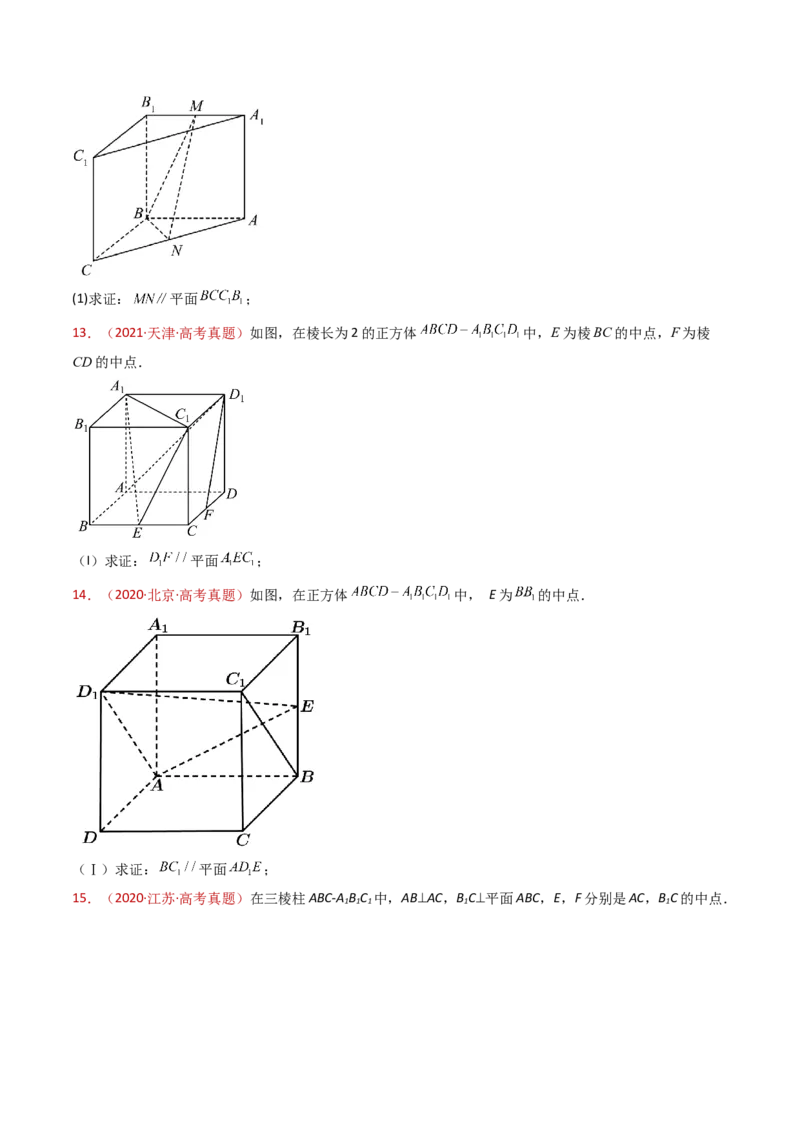
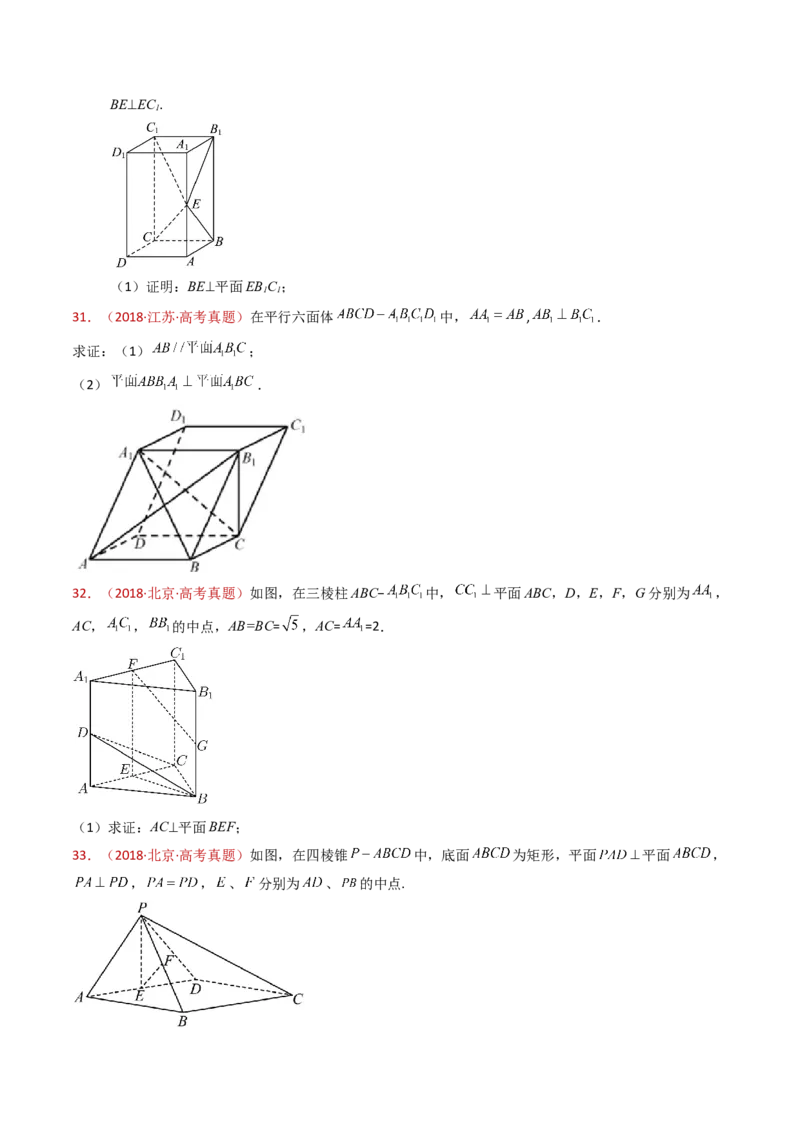
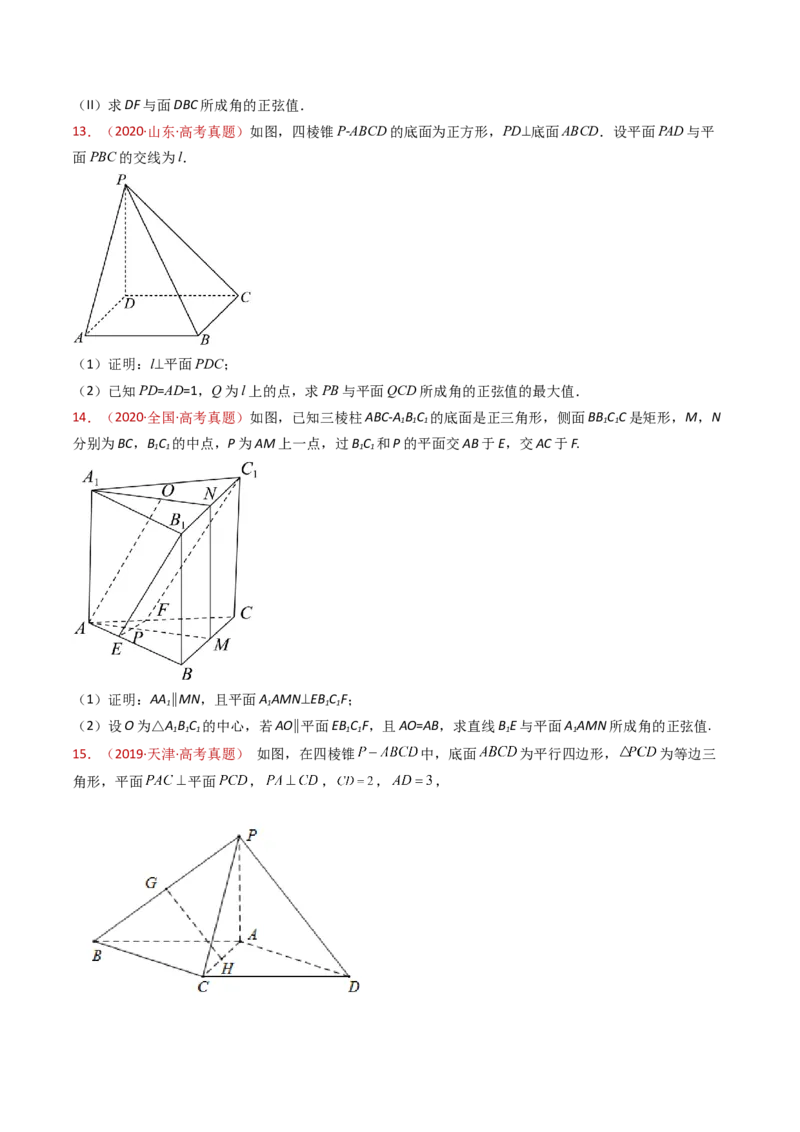
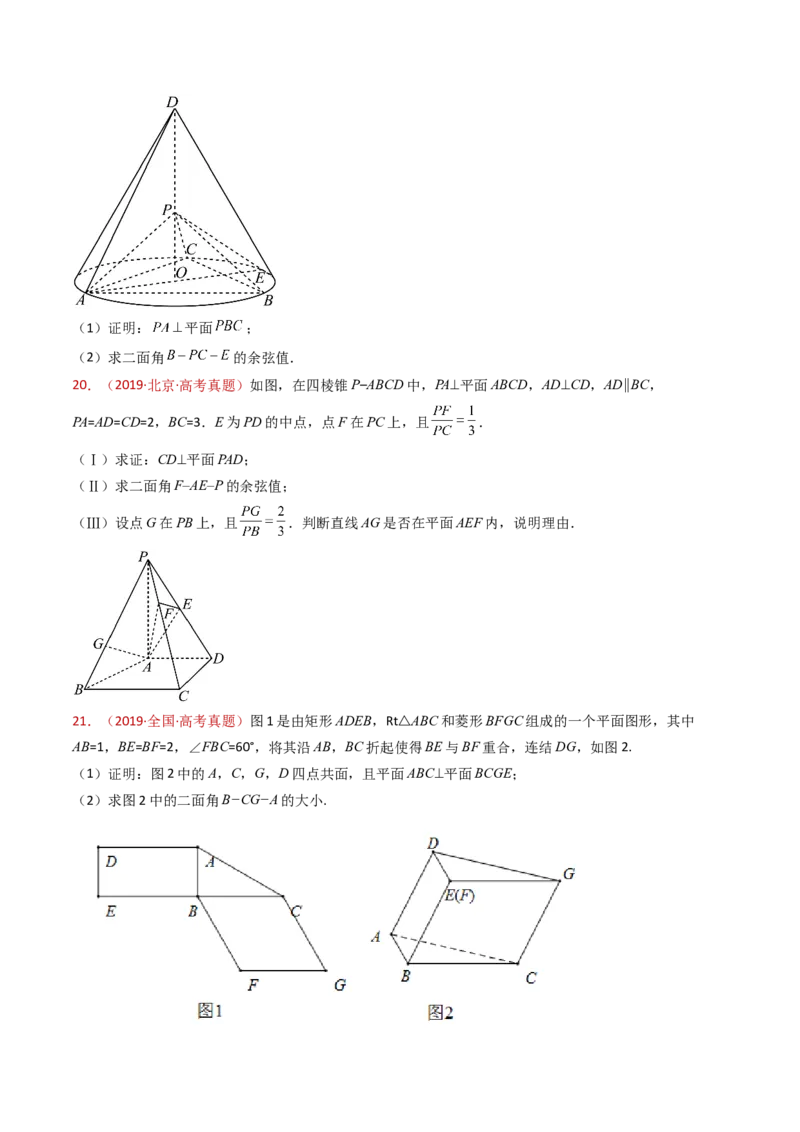
13.(2021·天津·高考真题)如图,在棱长为2的正方体 中,E为棱BC的中点,F为棱
CD的中点.
(I)求证: 平面 ;
14.(2020·北京·高考真题)如图,在正方体 中, E为 的中点.
(Ⅰ)求证: 平面 ;
15.(2020·江苏·高考真题)在三棱柱ABC-A B C 中,AB⊥AC,B C⊥平面ABC,E,F分别是AC,B C的中点.
1 1 1 1 1(1)求证:EF∥平面AB C ;
1 1
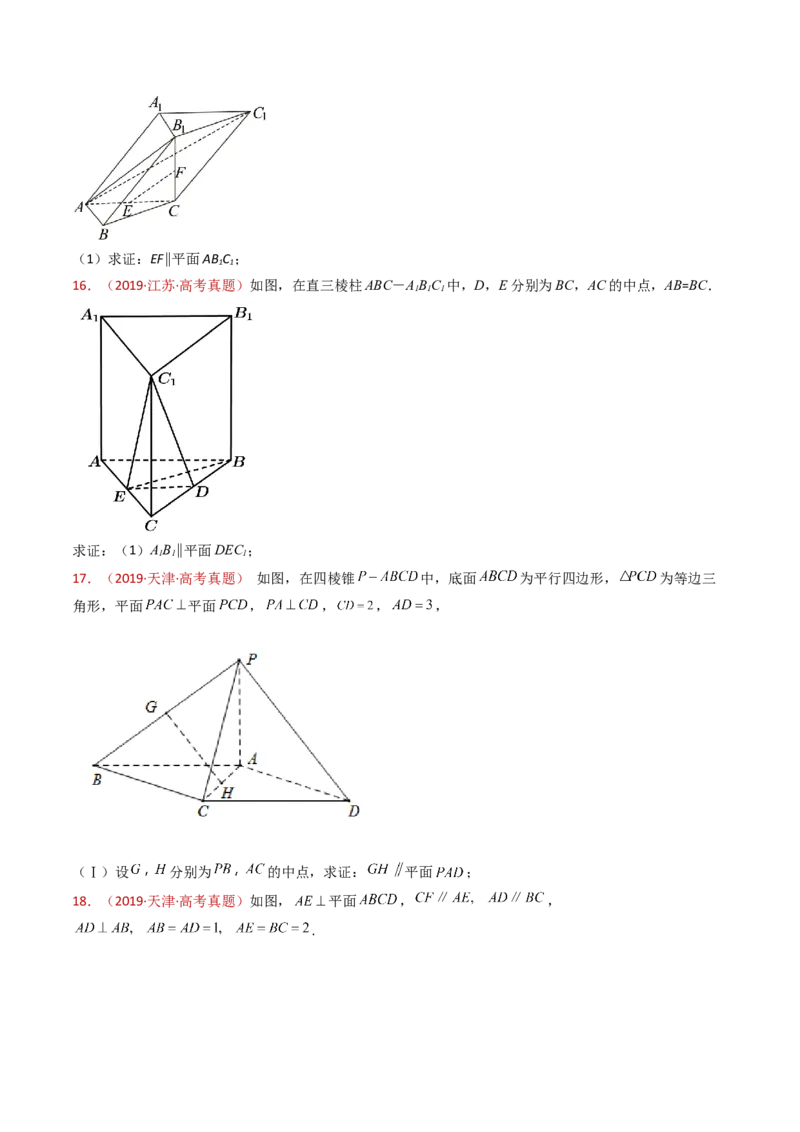
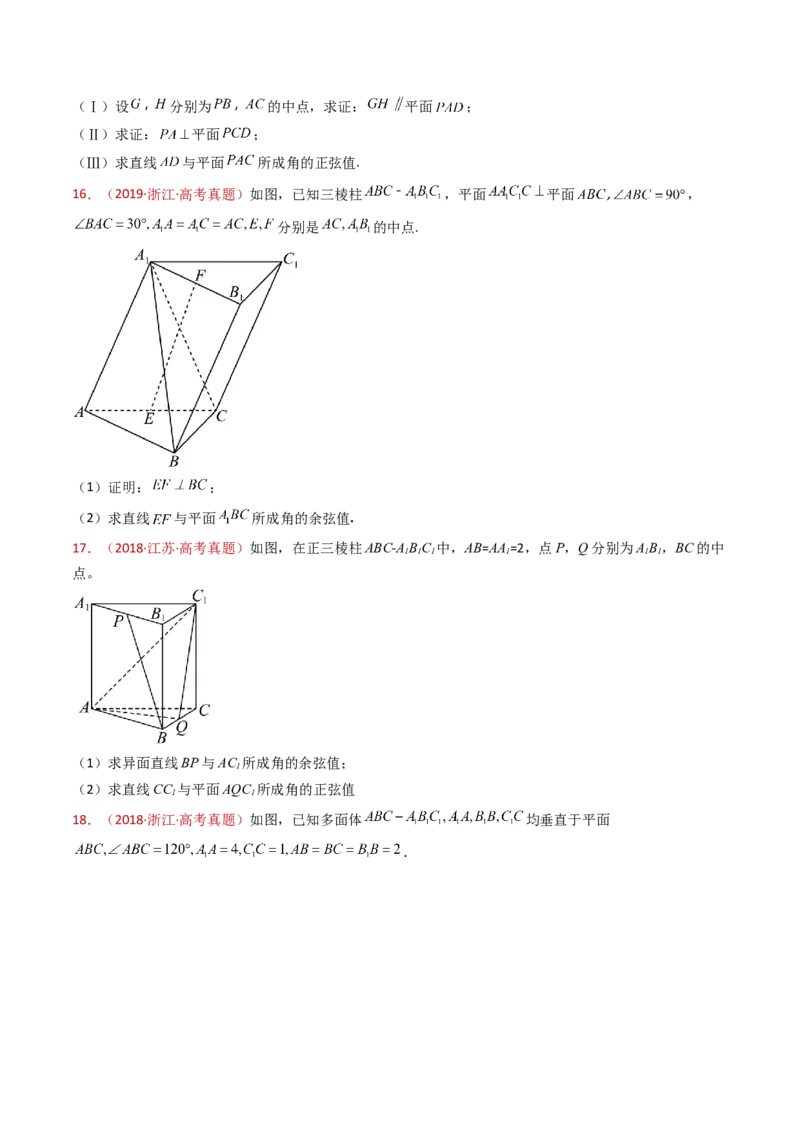
16.(2019·江苏·高考真题)如图,在直三棱柱ABC-ABC 中,D,E分别为BC,AC的中点,AB=BC.
1 1 1
求证:(1)AB∥平面DEC ;
1 1 1
17.(2019·天津·高考真题) 如图,在四棱锥 中,底面 为平行四边形, 为等边三
角形,平面 平面 , , , ,
(Ⅰ)设 分别为 的中点,求证: 平面 ;
18.(2019·天津·高考真题)如图, 平面 , ,
.(Ⅰ)求证: 平面 ;
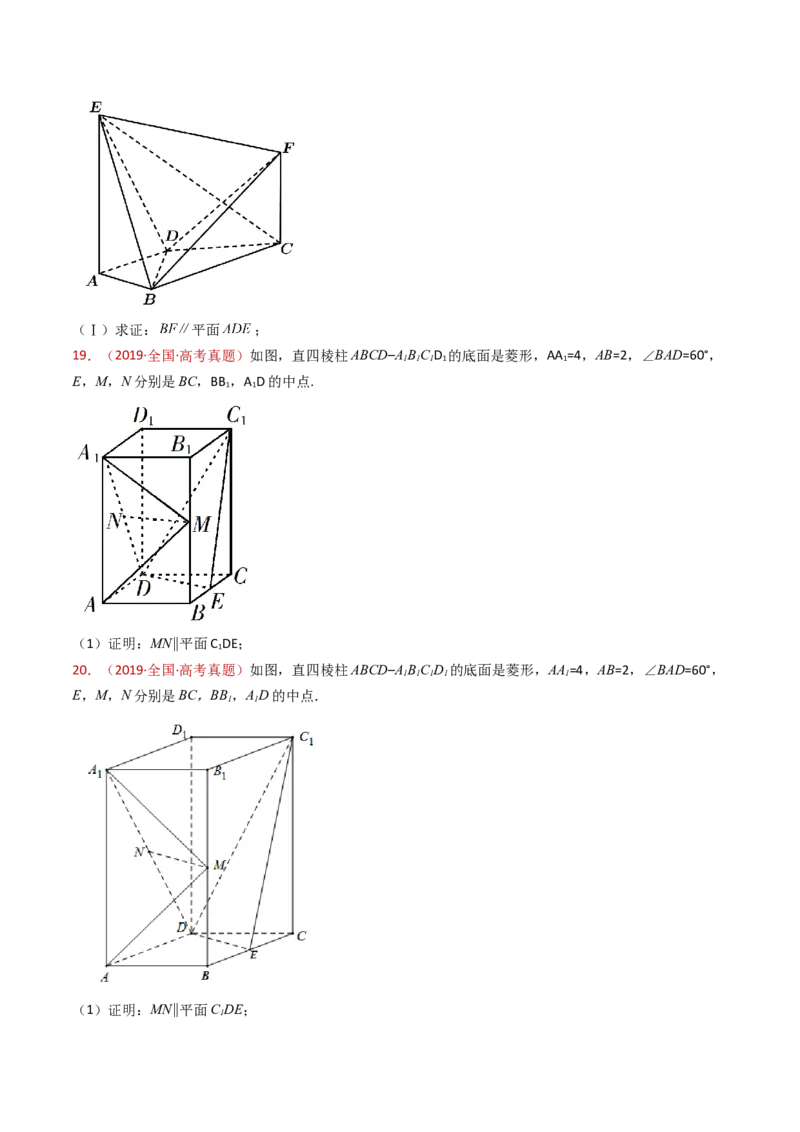
19.(2019·全国·高考真题)如图,直四棱柱ABCD–ABC D 的底面是菱形,AA =4,AB=2,∠BAD=60°,
1 1 1 1 1
E,M,N分别是BC,BB ,A D的中点.
1 1
(1)证明:MN∥平面C DE;
1
20.(2019·全国·高考真题)如图,直四棱柱ABCD–ABC D 的底面是菱形,AA=4,AB=2,∠BAD=60°,
1 1 1 1 1
E,M,N分别是BC,BB,AD的中点.
1 1
(1)证明:MN∥平面C DE;
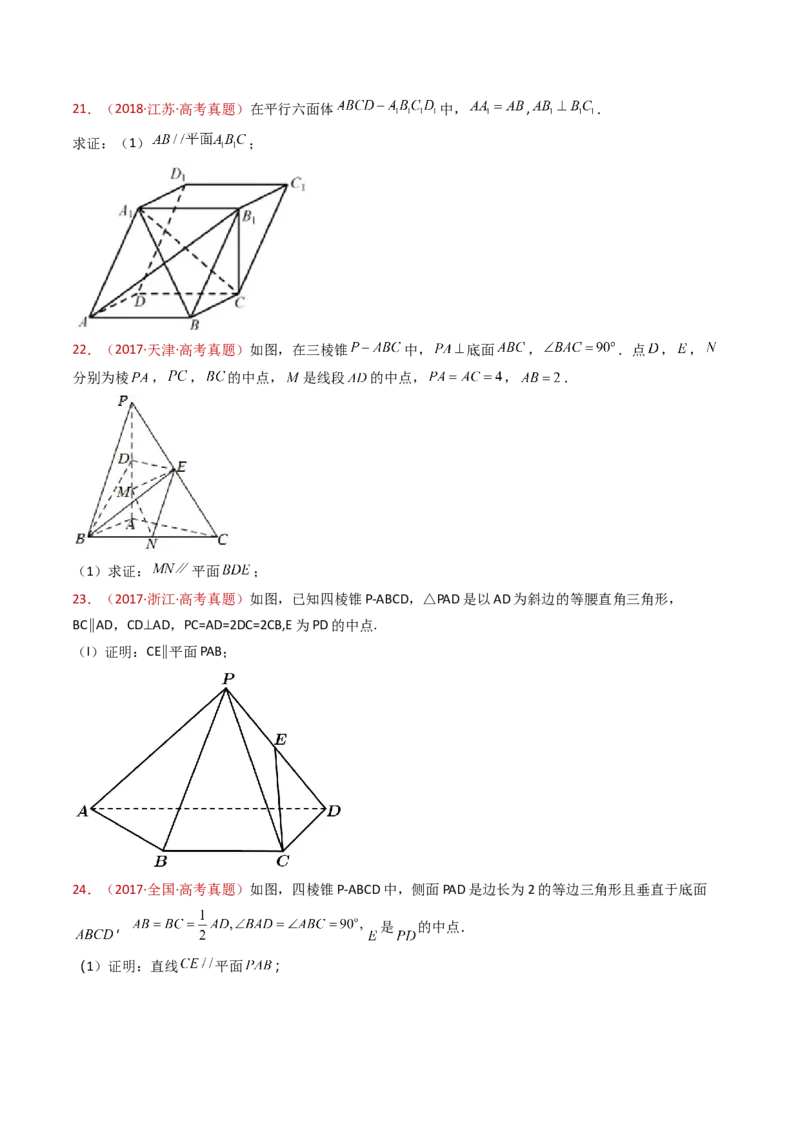
121.(2018·江苏·高考真题)在平行六面体 中, , .
求证:(1) ;
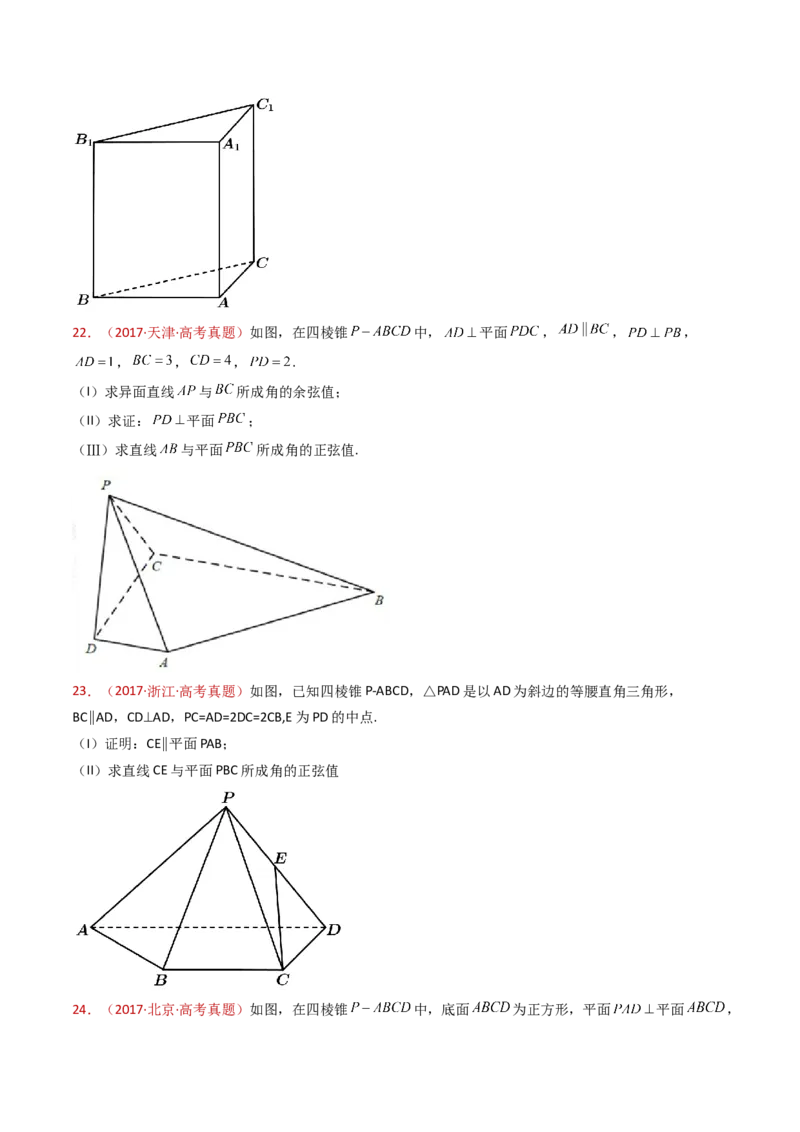
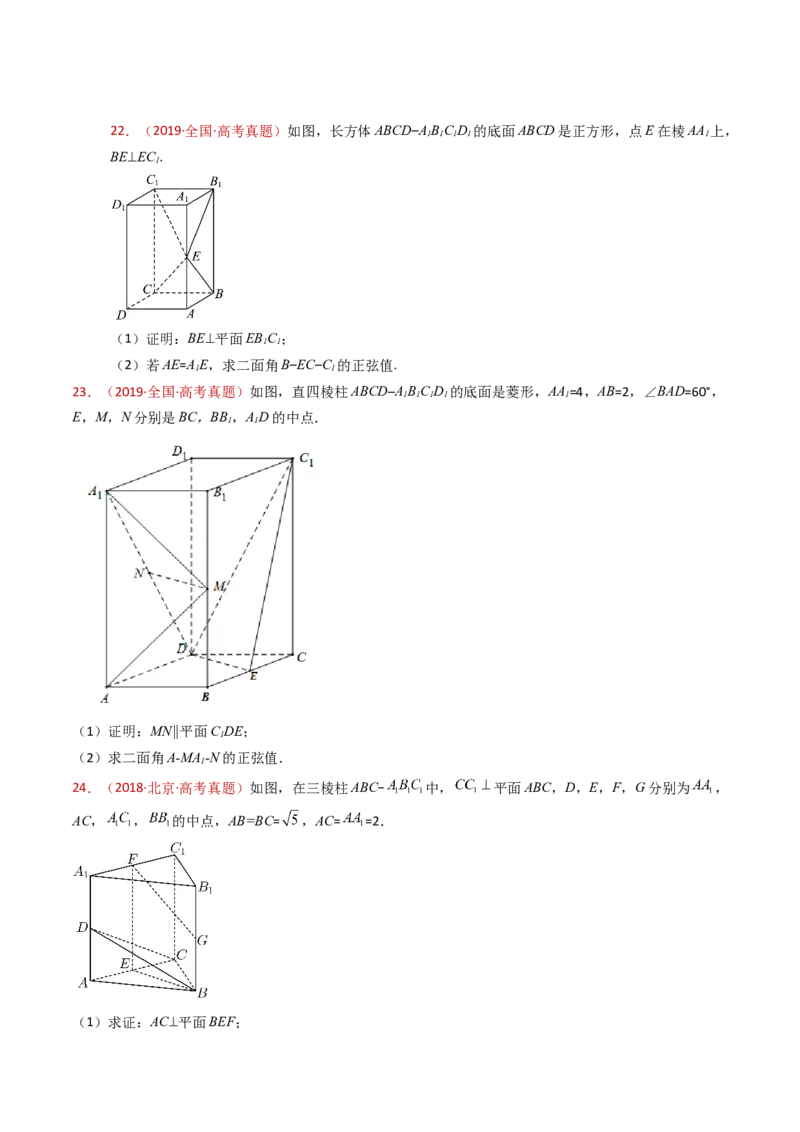
22.(2017·天津·高考真题)如图,在三棱锥 中, 底面 , .点 , ,
分别为棱 , , 的中点, 是线段 的中点, , .
(1)求证: 平面 ;
23.(2017·浙江·高考真题)如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,
BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(I)证明:CE∥平面PAB;
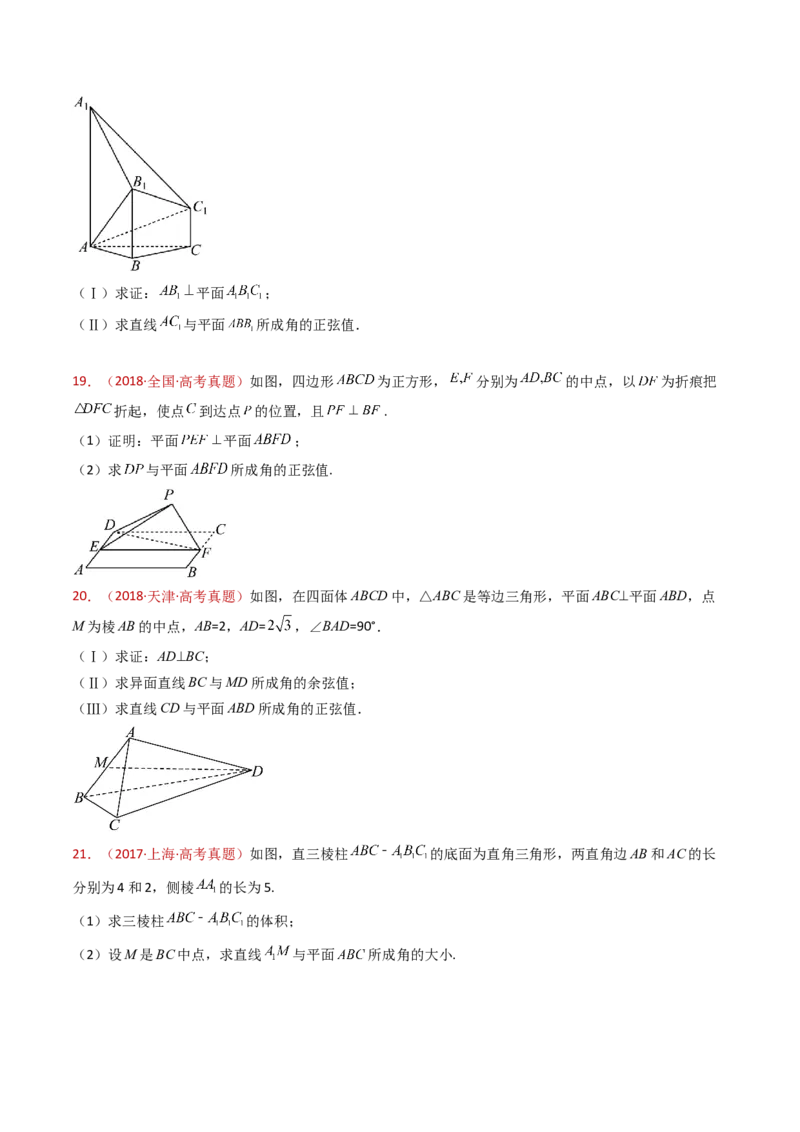
24.(2017·全国·高考真题)如图,四棱锥P-ABCD中,侧面PAD是边长为2的等边三角形且垂直于底面
, 是 的中点.
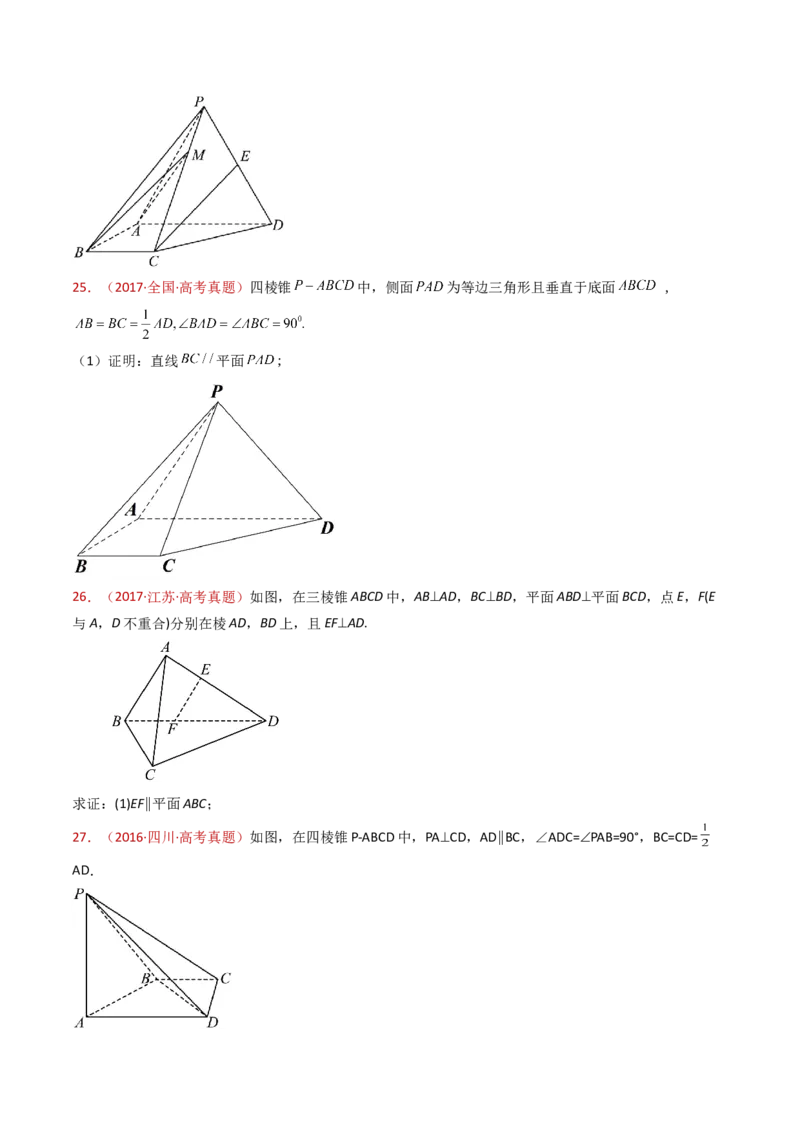
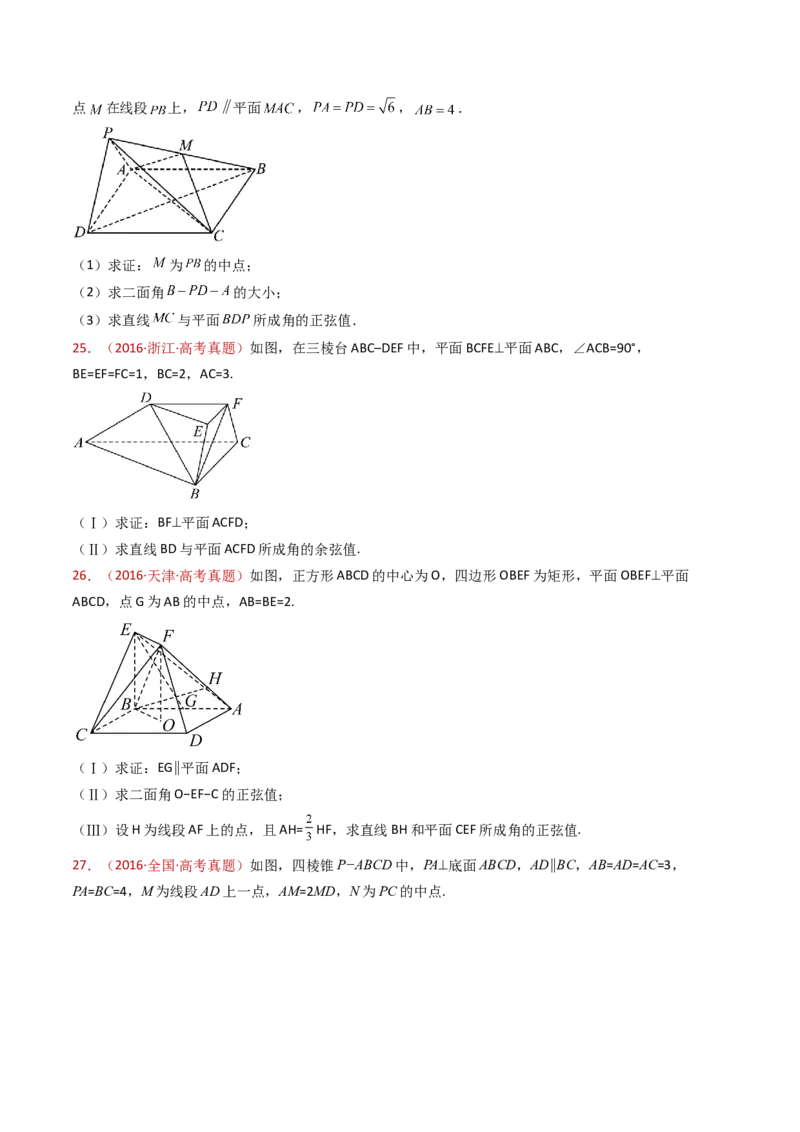
(1)证明:直线 平面 ;25.(2017·全国·高考真题)四棱锥 中,侧面 为等边三角形且垂直于底面 ,
(1)证明:直线 平面 ;
26.(2017·江苏·高考真题)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E
与A,D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
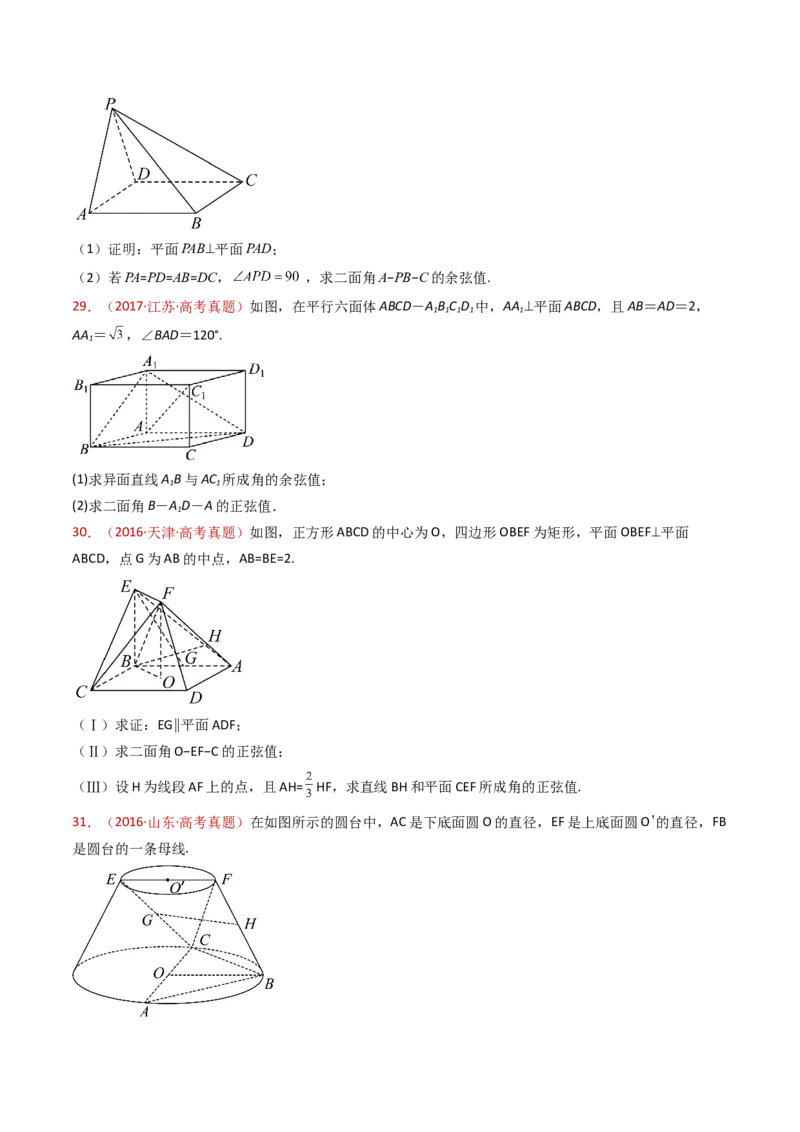
27.(2016·四川·高考真题)如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=
AD.(Ⅰ)在平面PAD内找一点M,使得直线CM∥平面PAB,并说明理由;
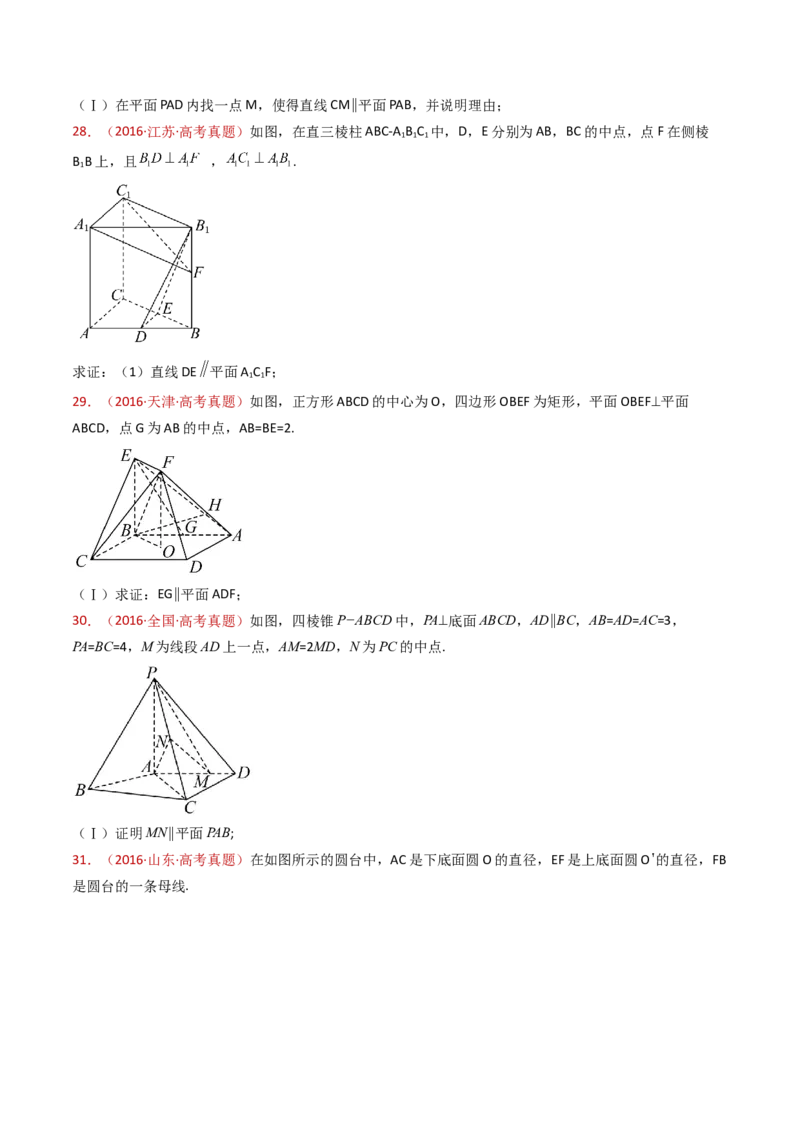
28.(2016·江苏·高考真题)如图,在直三棱柱ABC-A B C 中,D,E分别为AB,BC的中点,点F在侧棱
1 1 1
B B上,且 , .
1
求证:(1)直线DE 平面A C F;
1 1
29.(2016·天津·高考真题)如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面
ABCD,点G为AB的中点,AB=BE=2.
(Ⅰ)求证:EG∥平面ADF;
30.(2016·全国·高考真题)如图,四棱锥P−ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,
PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(Ⅰ)证明MN∥平面PAB;
31.(2016·山东·高考真题)在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O 的直径,FB
是圆台的一条母线.(Ⅰ)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
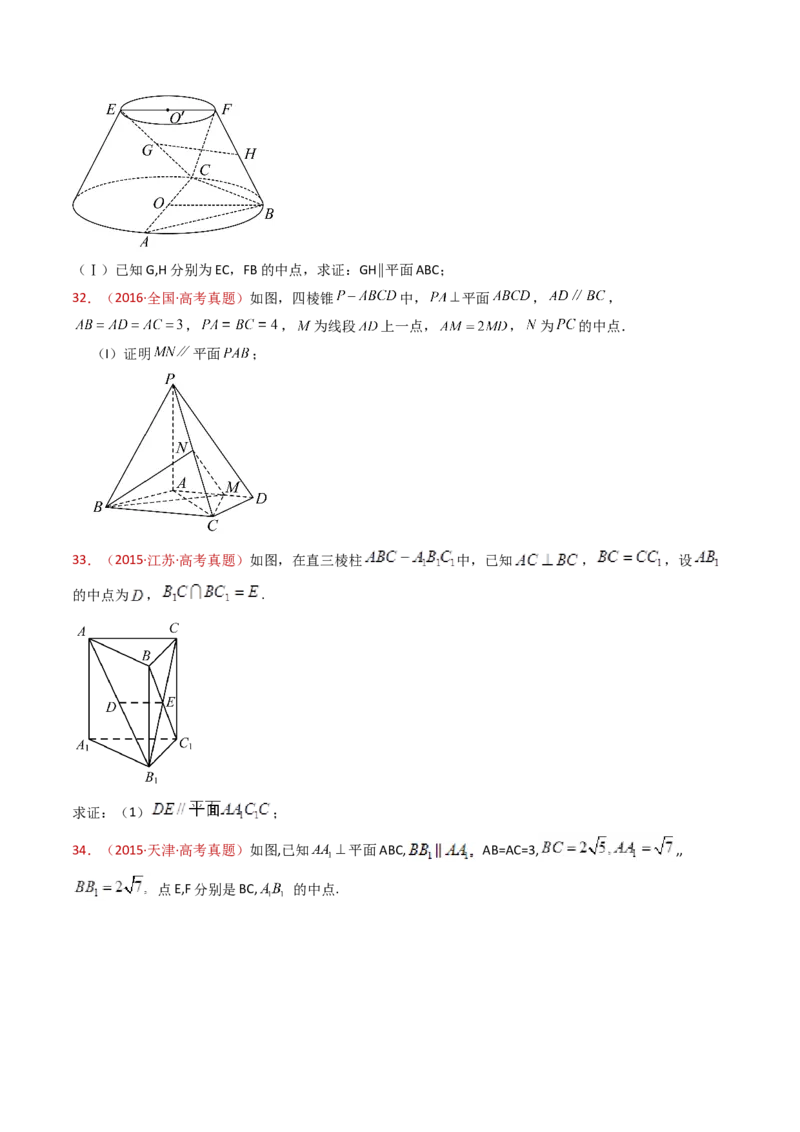
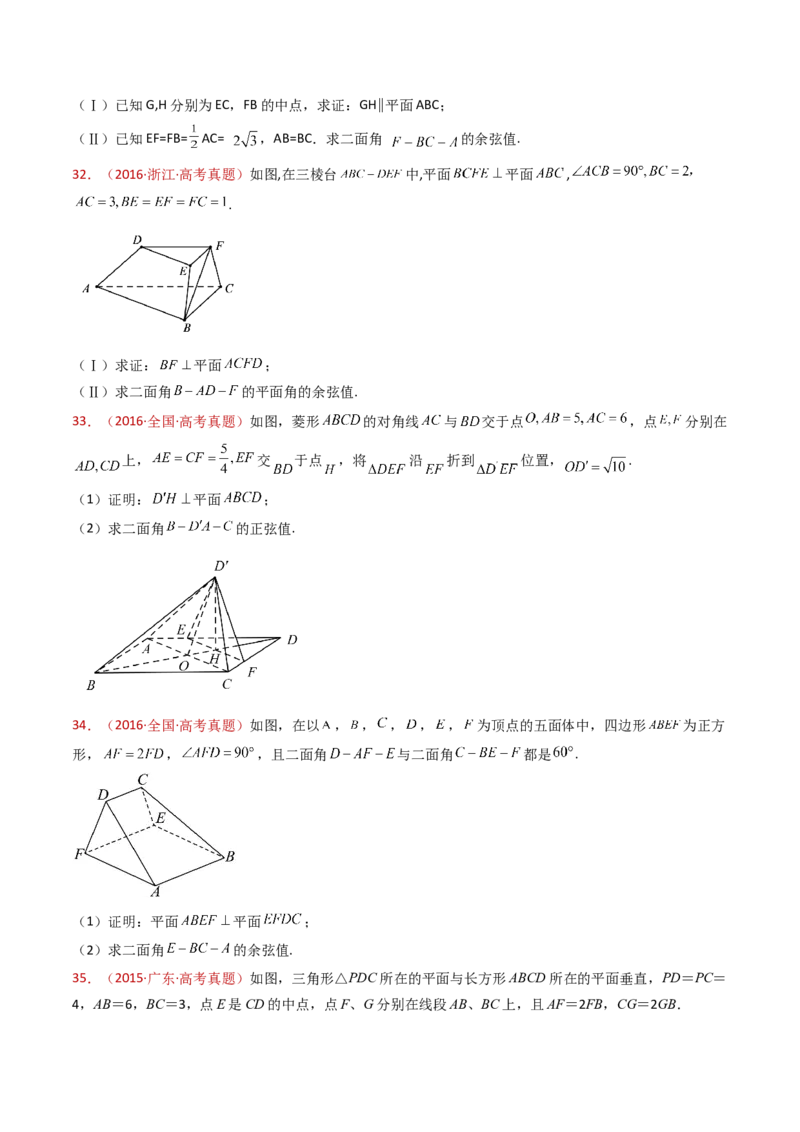
32.(2016·全国·高考真题)如图,四棱锥 中, 平面 , ,
, , 为线段 上一点, , 为 的中点.
(I)证明 平面 ;
33.(2015·江苏·高考真题)如图,在直三棱柱 中,已知 , ,设
的中点为 , .
求证:(1) ;
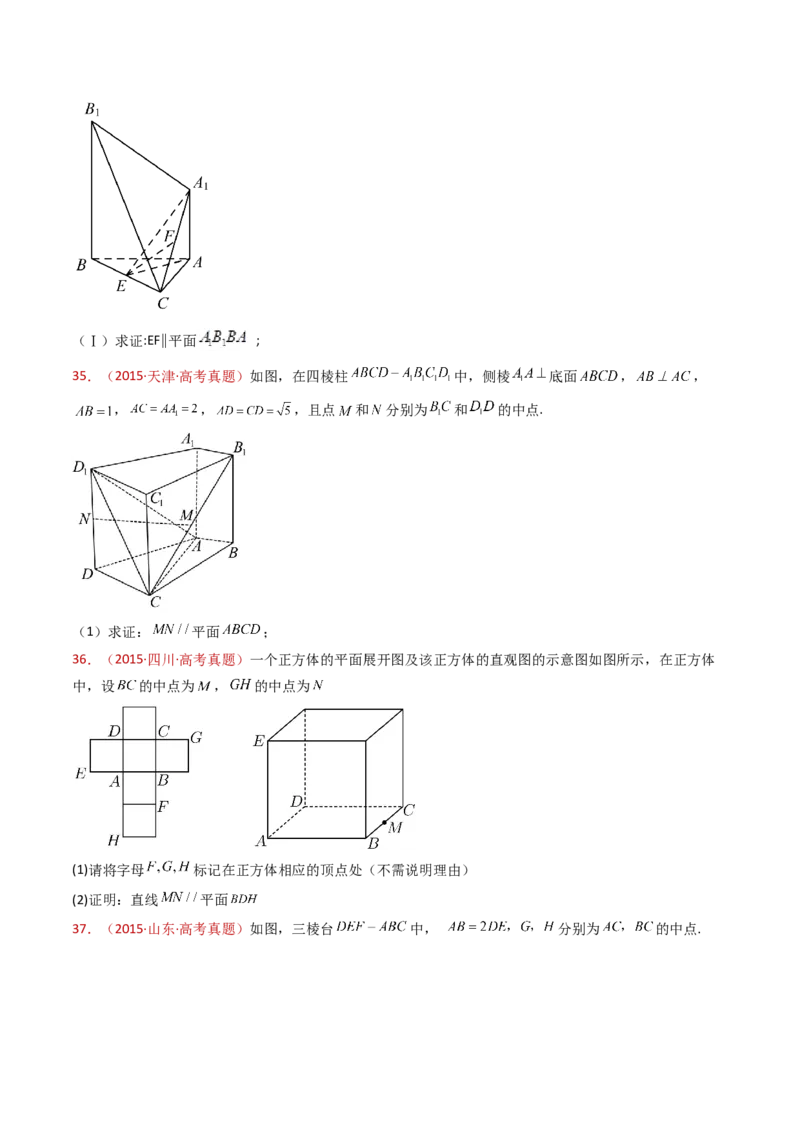
34.(2015·天津·高考真题)如图,已知 平面ABC, AB=AC=3, ,,
点E,F分别是BC, 的中点.(Ⅰ)求证:EF∥平面 ;
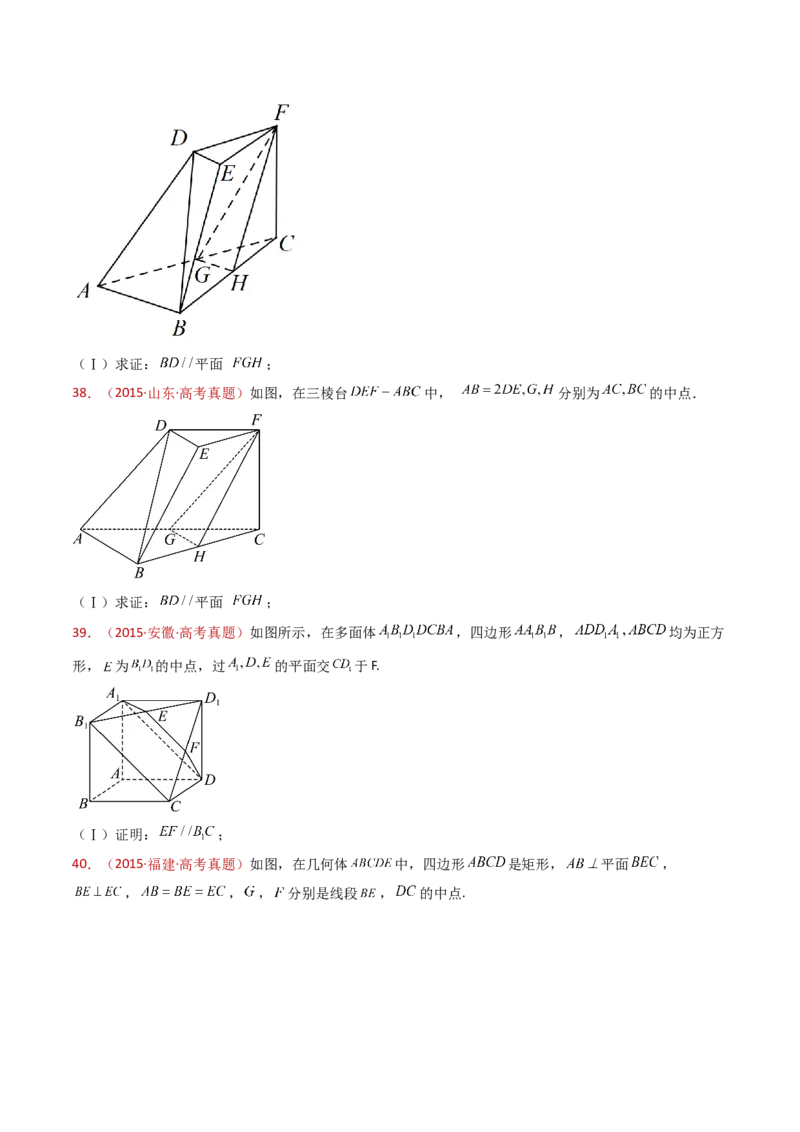
35.(2015·天津·高考真题)如图,在四棱柱 中,侧棱 底面 , ,
, , ,且点 和 分别为 和 的中点.
(1)求证: 平面 ;
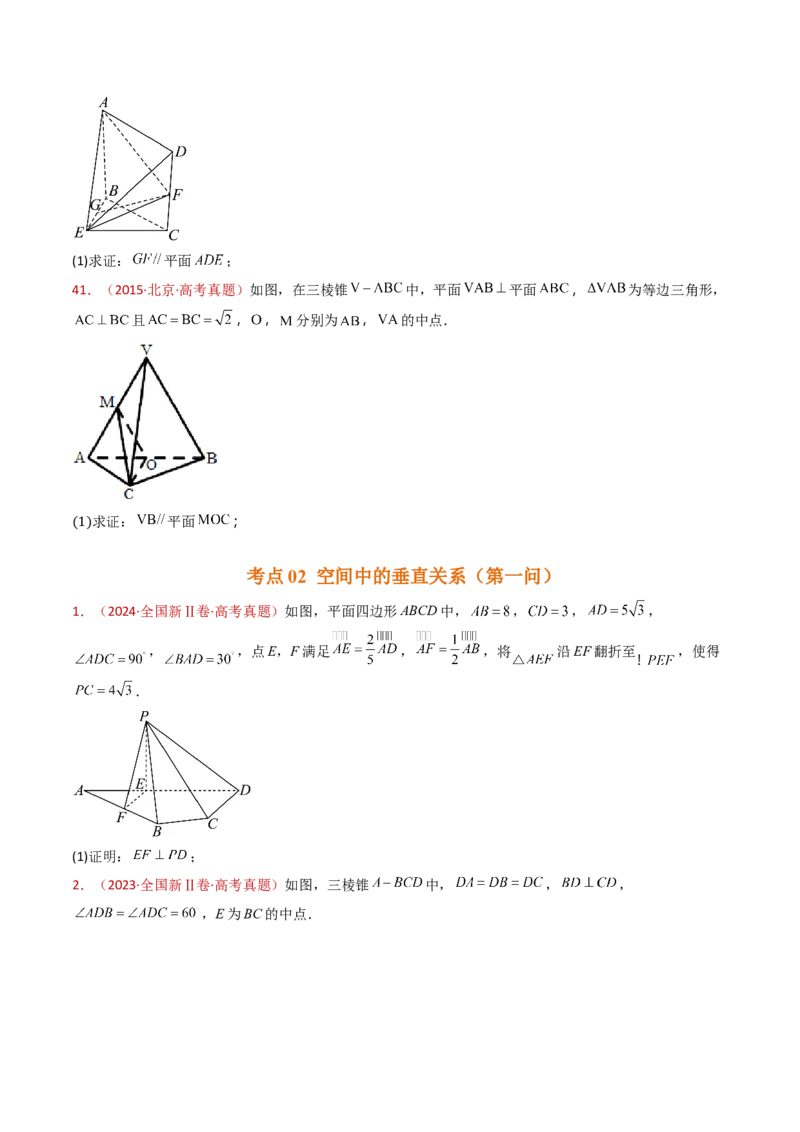
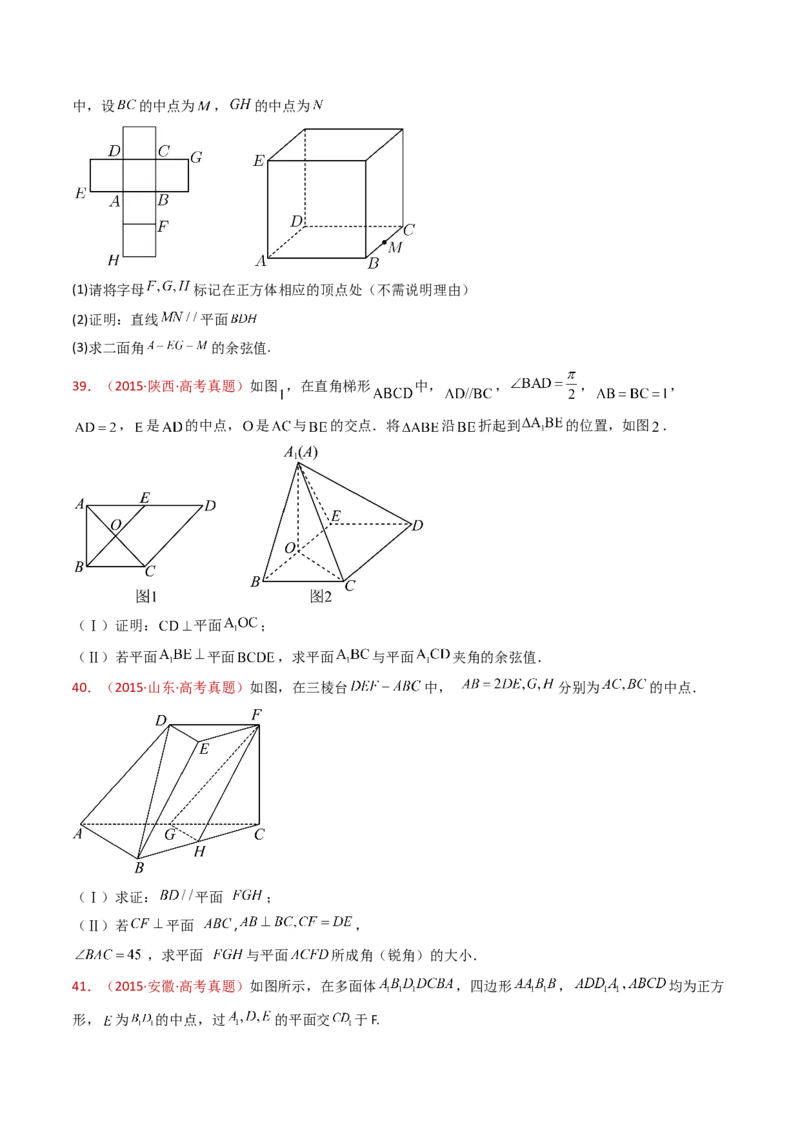
36.(2015·四川·高考真题)一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体
中,设 的中点为 , 的中点为
(1)请将字母 标记在正方体相应的顶点处(不需说明理由)
(2)证明:直线 平面
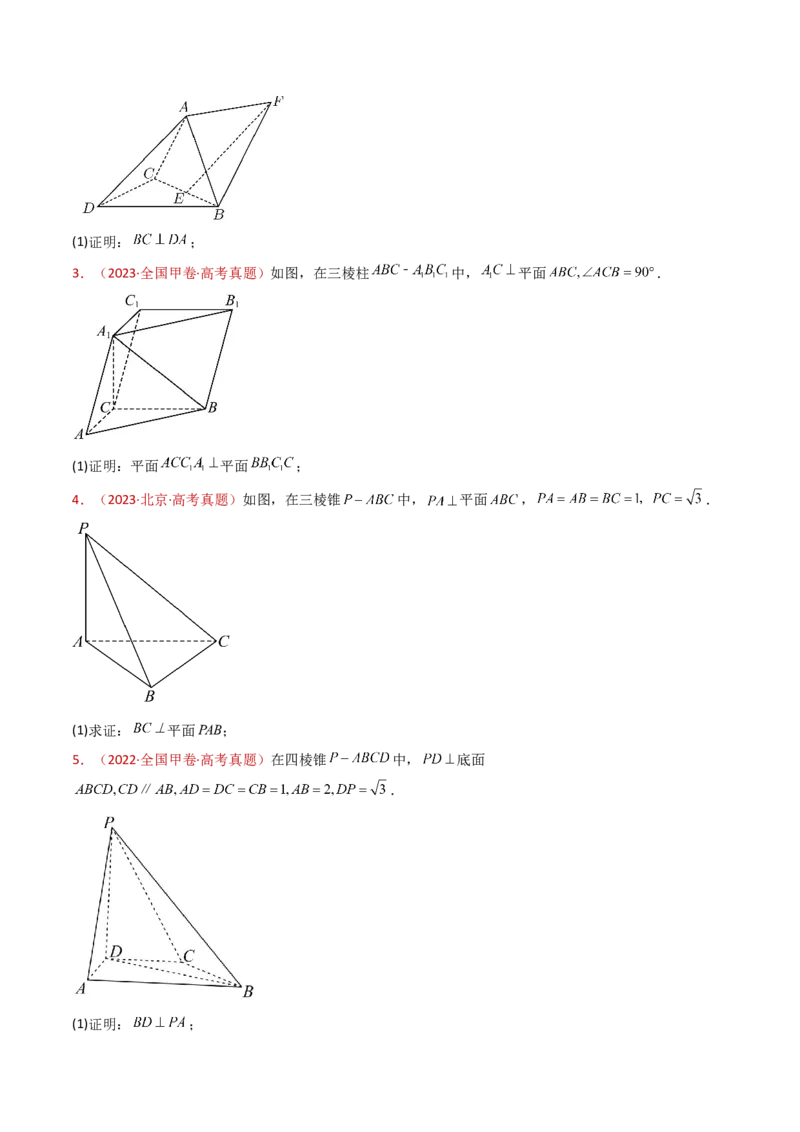
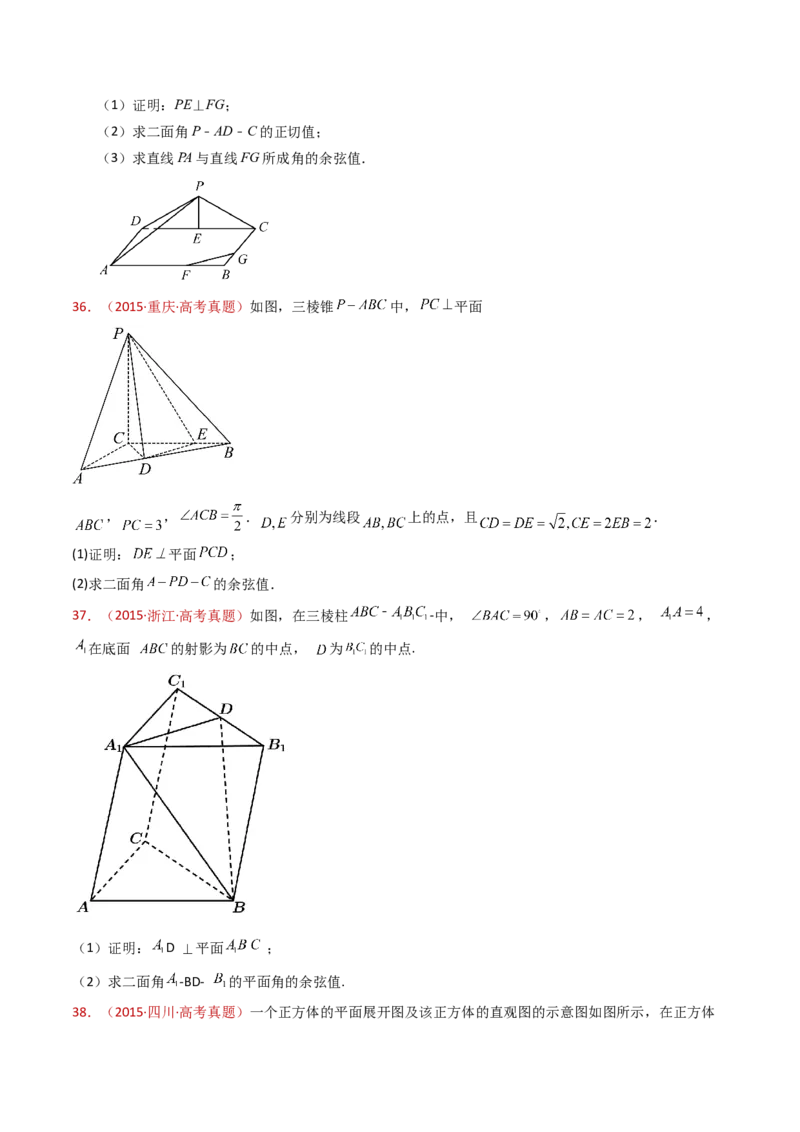
37.(2015·山东·高考真题)如图,三棱台 中, 分别为 的中点.(Ⅰ)求证: 平面 ;
38.(2015·山东·高考真题)如图,在三棱台 中, 分别为 的中点.
(Ⅰ)求证: 平面 ;
39.(2015·安徽·高考真题)如图所示,在多面体 ,四边形 , 均为正方
形, 为 的中点,过 的平面交 于F.
(Ⅰ)证明: ;
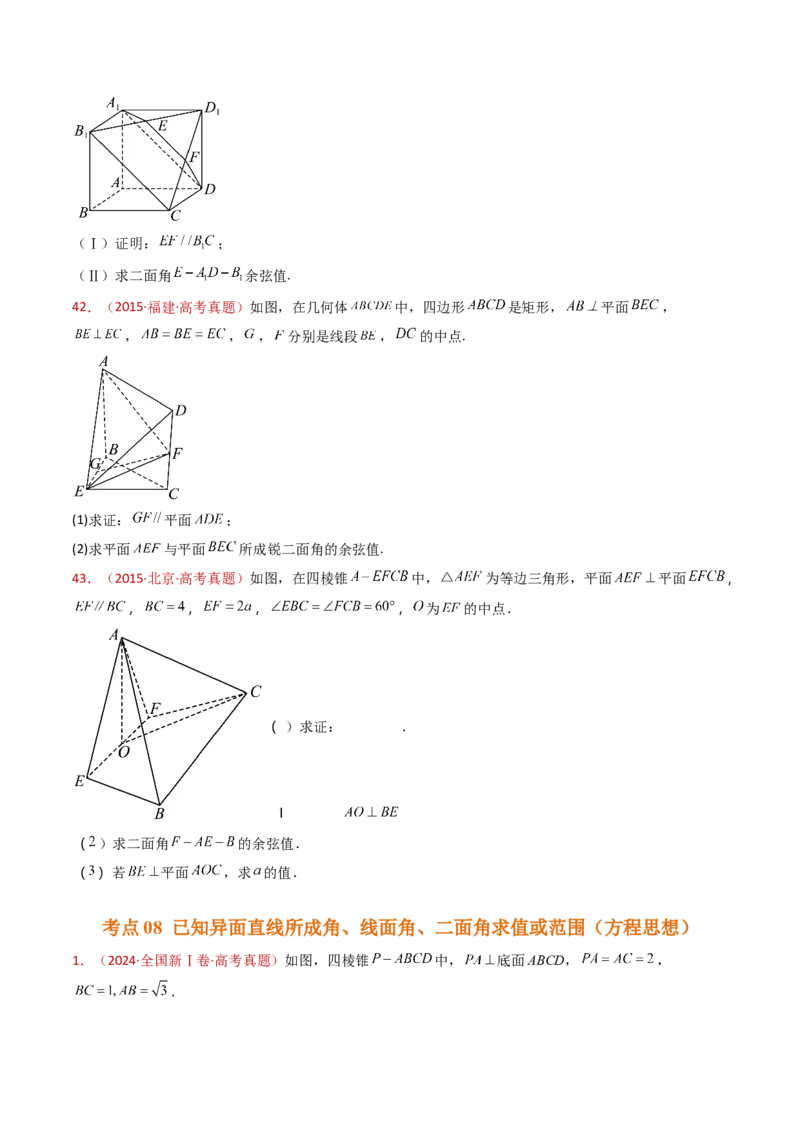
40.(2015·福建·高考真题)如图,在几何体 中,四边形 是矩形, 平面 ,
, , , 分别是线段 , 的中点.(1)求证: 平面 ;
41.(2015·北京·高考真题)如图,在三棱锥 中,平面 平面 , 为等边三角形,
且 , , 分别为 , 的中点.
求证: 平面 ;
(1)
考点02 空间中的垂直关系(第一问)
1.(2024·全国新Ⅱ卷·高考真题)如图,平面四边形ABCD中, , , ,
, ,点E,F满足 , ,将 沿EF翻折至 ,使得
.
(1)证明: ;
2.(2023·全国新Ⅱ卷·高考真题)如图,三棱锥 中, , ,
,E为BC的中点.(1)证明: ;
3.(2023·全国甲卷·高考真题)如图,在三棱柱 中, 平面 .
(1)证明:平面 平面 ;
4.(2023·北京·高考真题)如图,在三棱锥 中, 平面 , .
(1)求证: 平面PAB;
5.(2022·全国甲卷·高考真题)在四棱锥 中, 底面
.
(1)证明: ;6.(2022·全国乙卷·高考真题)如图,四面体 中, ,E为 的
中点.
(1)证明:平面 平面 ;
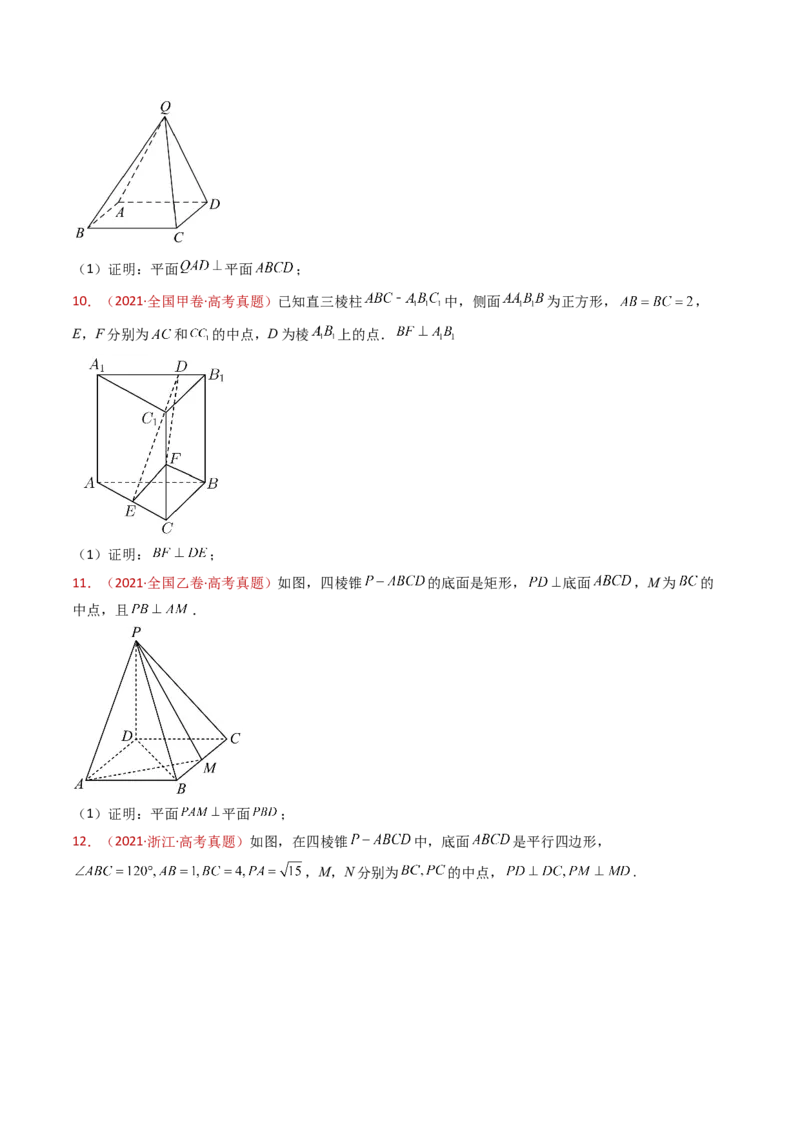
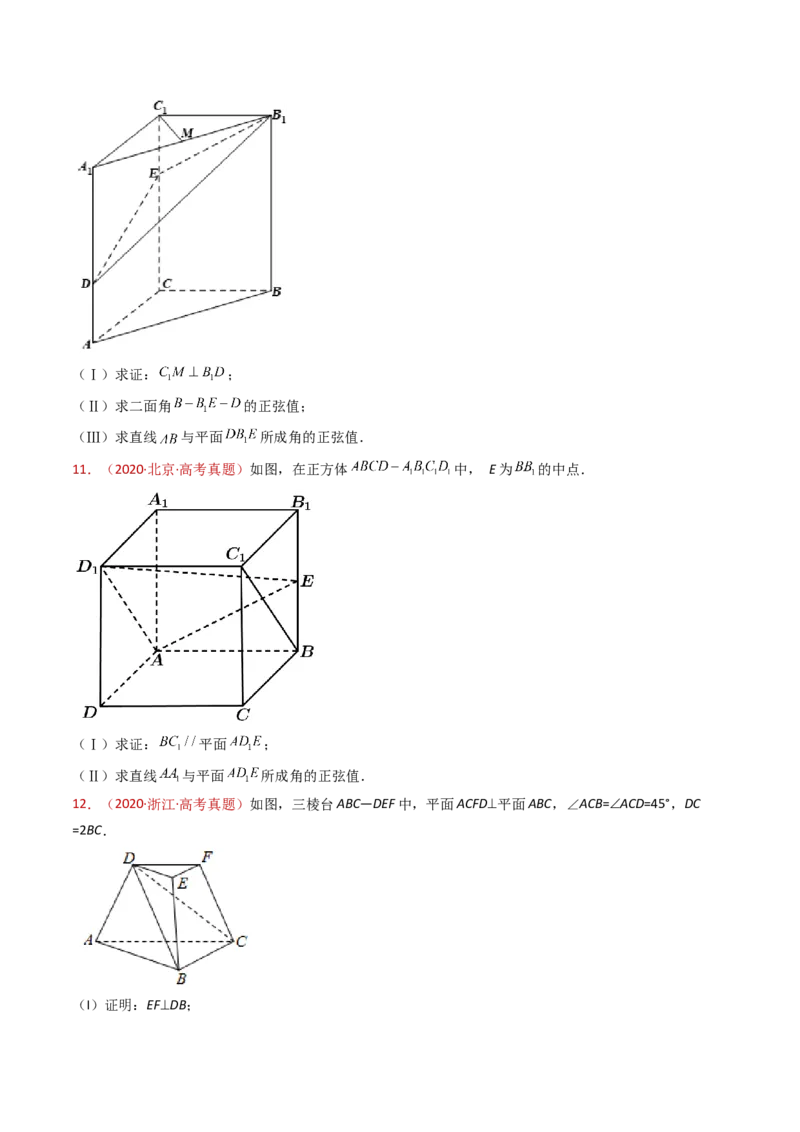
7.(2022·浙江·高考真题)如图,已知 和 都是直角梯形, , , ,
, , ,二面角 的平面角为 .设M,N分别为 的
中点.
(1)证明: ;
8.(2021·全国新Ⅰ卷·高考真题)如图,在三棱锥 中,平面 平面 , , 为
的中点.
(1)证明: ;
9.(2021·全国新Ⅱ卷·高考真题)在四棱锥 中,底面 是正方形,若
.(1)证明:平面 平面 ;
10.(2021·全国甲卷·高考真题)已知直三棱柱 中,侧面 为正方形, ,
E,F分别为 和 的中点,D为棱 上的点.
(1)证明: ;
11.(2021·全国乙卷·高考真题)如图,四棱锥 的底面是矩形, 底面 ,M为 的
中点,且 .
(1)证明:平面 平面 ;
12.(2021·浙江·高考真题)如图,在四棱锥 中,底面 是平行四边形,
,M,N分别为 的中点, .(1)证明: ;
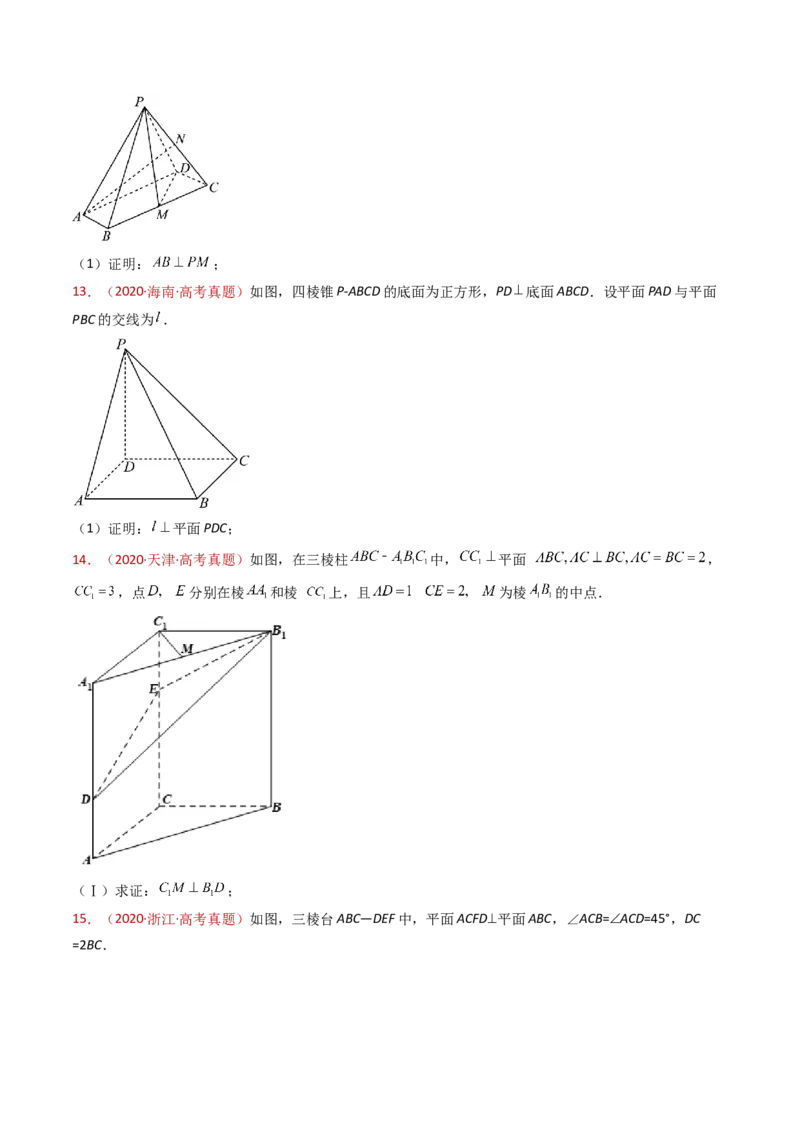
13.(2020·海南·高考真题)如图,四棱锥P-ABCD的底面为正方形,PD 底面ABCD.设平面PAD与平面
PBC的交线为 .
(1)证明: 平面PDC;
14.(2020·天津·高考真题)如图,在三棱柱 中, 平面 ,
,点 分别在棱 和棱 上,且 为棱 的中点.
(Ⅰ)求证: ;
15.(2020·浙江·高考真题)如图,三棱台ABC—DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC
=2BC.(I)证明:EF⊥DB;
16.(2020·山东·高考真题)如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平
面PBC的交线为l.
(1)证明:l⊥平面PDC;
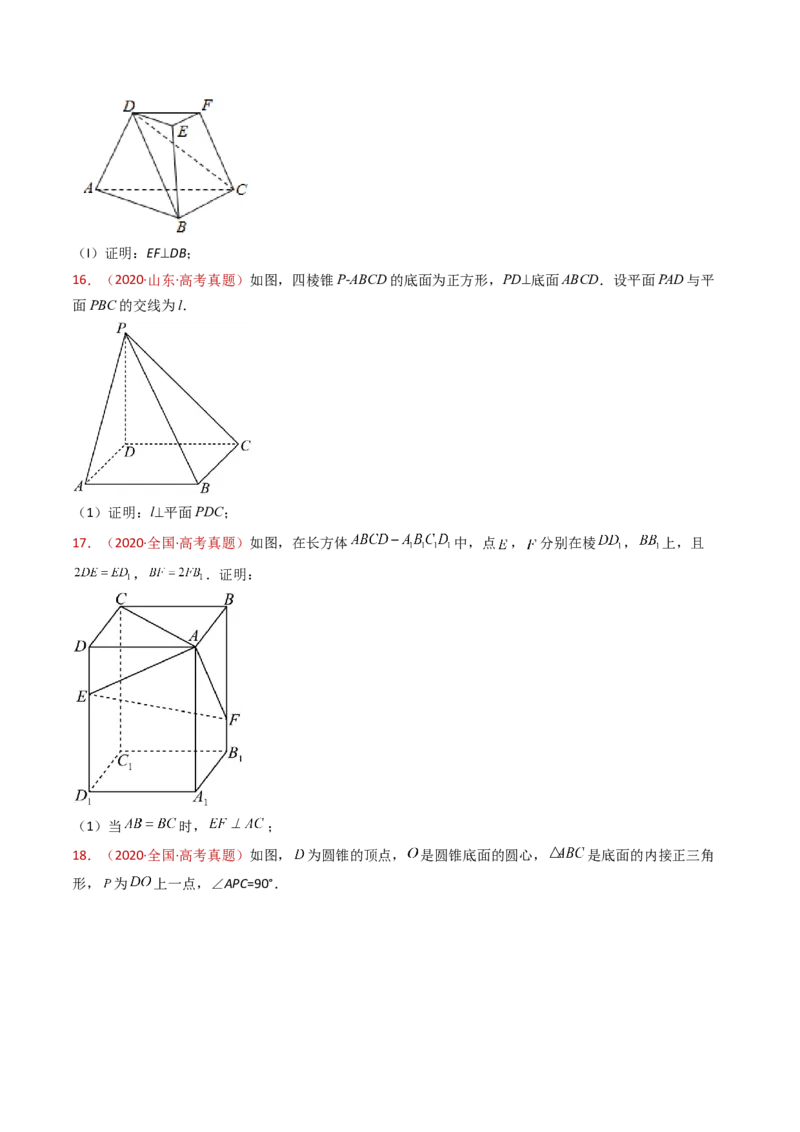
17.(2020·全国·高考真题)如图,在长方体 中,点 , 分别在棱 , 上,且
, .证明:
(1)当 时, ;
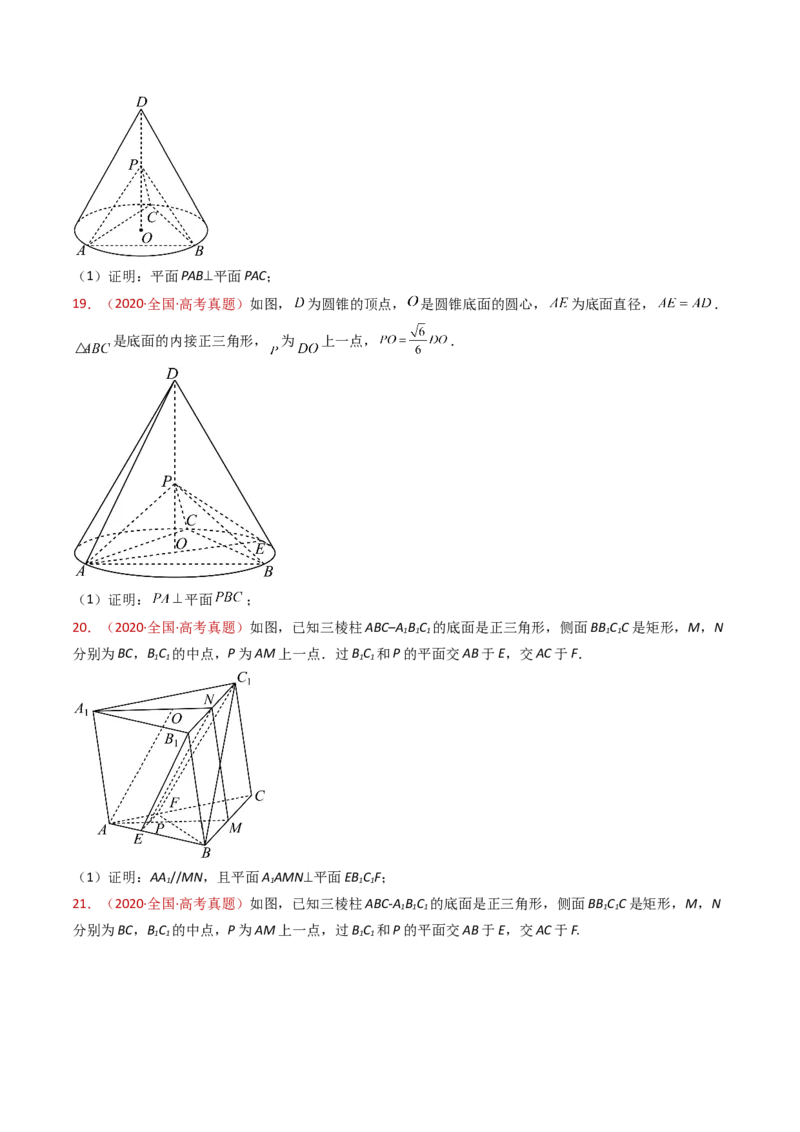
18.(2020·全国·高考真题)如图, 为圆锥的顶点, 是圆锥底面的圆心, 是底面的内接正三角
形, 为 上一点,∠APC=90°.(1)证明:平面PAB⊥平面PAC;
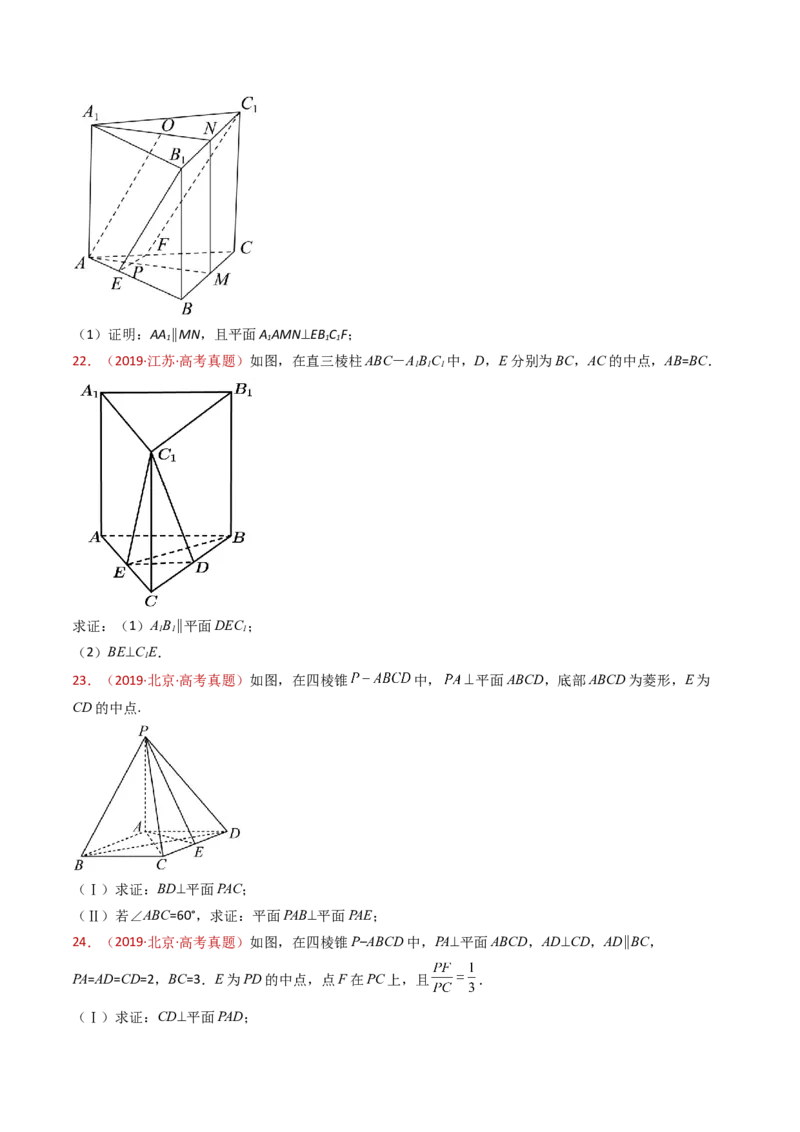
19.(2020·全国·高考真题)如图, 为圆锥的顶点, 是圆锥底面的圆心, 为底面直径, .
是底面的内接正三角形, 为 上一点, .
(1)证明: 平面 ;
20.(2020·全国·高考真题)如图,已知三棱柱ABC–A B C 的底面是正三角形,侧面BB C C是矩形,M,N
1 1 1 1 1
分别为BC,B C 的中点,P为AM上一点.过B C 和P的平面交AB于E,交AC于F.
1 1 1 1
(1)证明:AA //MN,且平面A AMN⊥平面EB C F;
1 1 1 1
21.(2020·全国·高考真题)如图,已知三棱柱ABC-A B C 的底面是正三角形,侧面BB C C是矩形,M,N
1 1 1 1 1
分别为BC,B C 的中点,P为AM上一点,过B C 和P的平面交AB于E,交AC于F.
1 1 1 1(1)证明:AA ∥MN,且平面A AMN⊥EB C F;
1 1 1 1
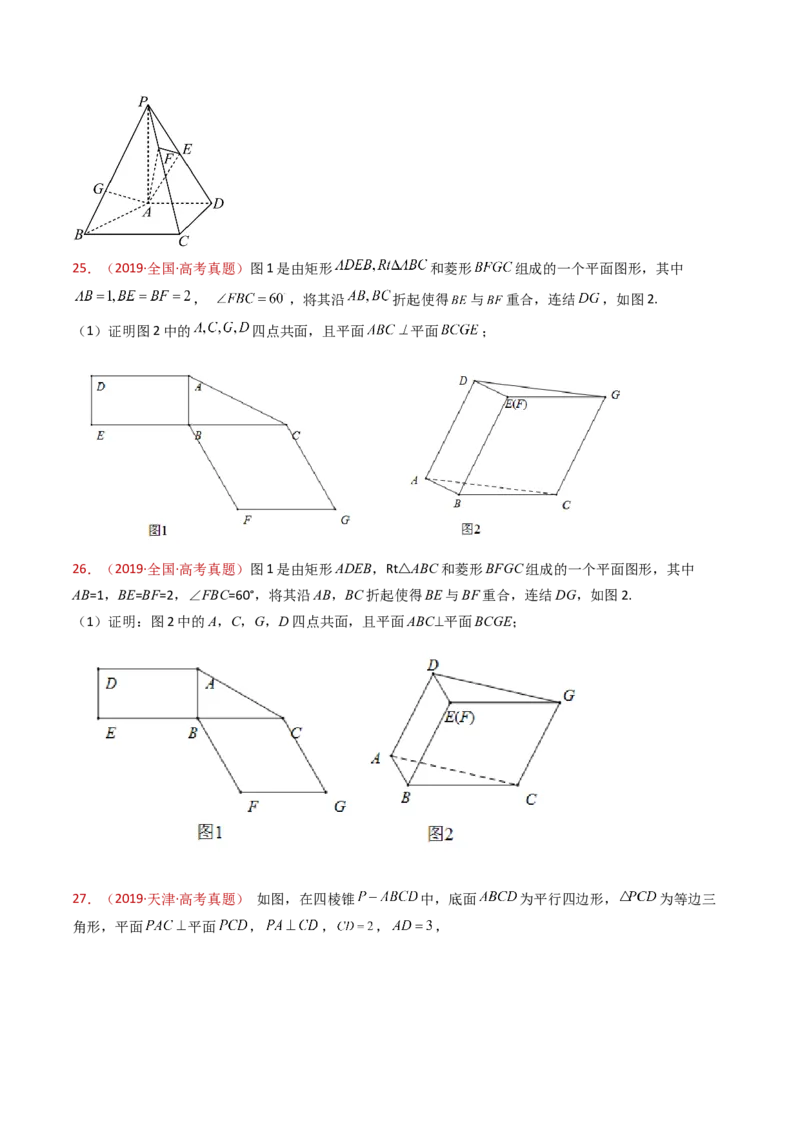
22.(2019·江苏·高考真题)如图,在直三棱柱ABC-ABC 中,D,E分别为BC,AC的中点,AB=BC.
1 1 1
求证:(1)AB∥平面DEC ;
1 1 1
(2)BE⊥C E.
1
23.(2019·北京·高考真题)如图,在四棱锥 中, 平面ABCD,底部ABCD为菱形,E为
CD的中点.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;
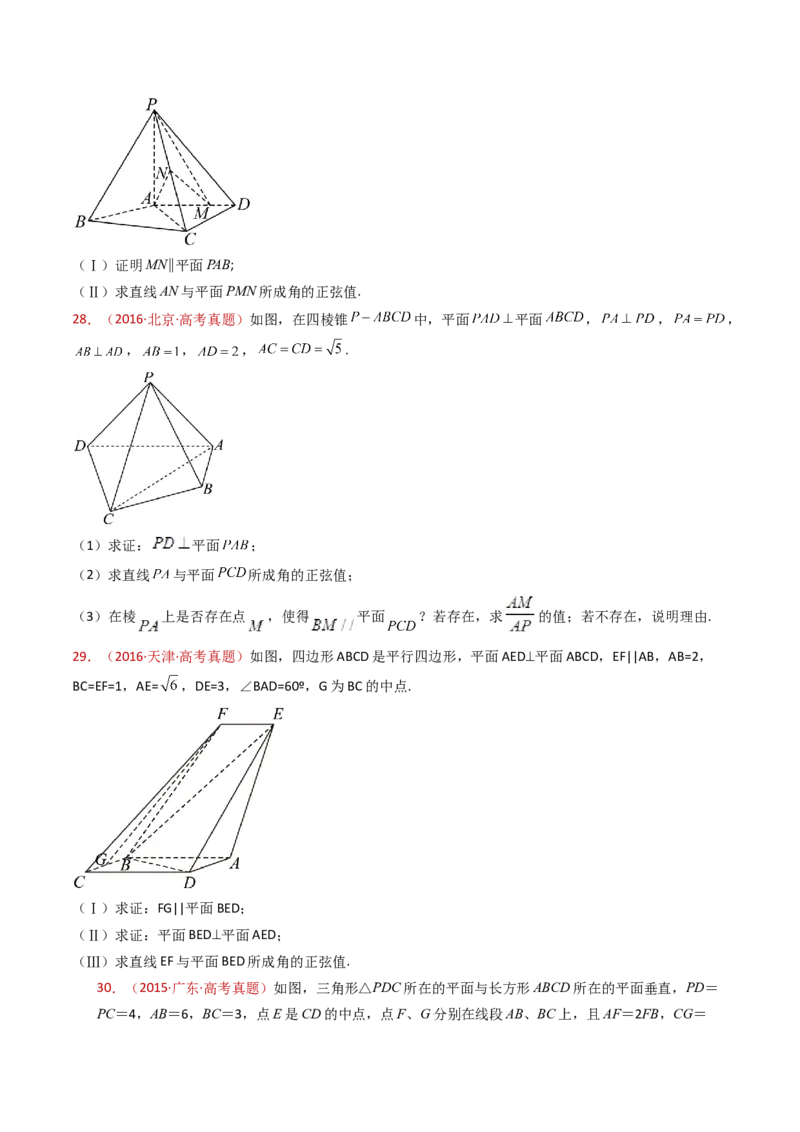
24.(2019·北京·高考真题)如图,在四棱锥P–ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,
PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且 .
(Ⅰ)求证:CD⊥平面PAD;25.(2019·全国·高考真题)图1是由矩形 和菱形 组成的一个平面图形,其中
, ,将其沿 折起使得 与 重合,连结 ,如图2.
(1)证明图2中的 四点共面,且平面 平面 ;
26.(2019·全国·高考真题)图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中
AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
27.(2019·天津·高考真题) 如图,在四棱锥 中,底面 为平行四边形, 为等边三
角形,平面 平面 , , , ,(Ⅰ)设 分别为 的中点,求证: 平面 ;
(Ⅱ)求证: 平面 ;
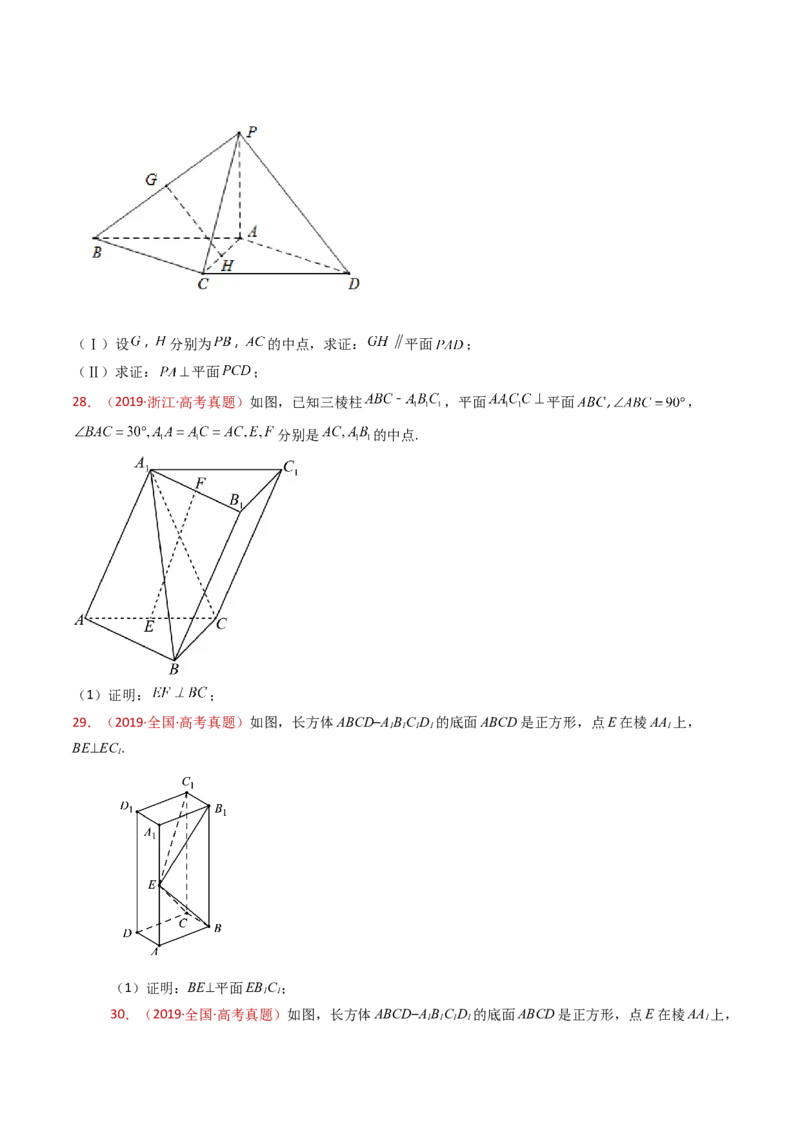
28.(2019·浙江·高考真题)如图,已知三棱柱 ,平面 平面 , ,
分别是 的中点.
(1)证明: ;
29.(2019·全国·高考真题)如图,长方体ABCD–ABC D 的底面ABCD是正方形,点E在棱AA 上,
1 1 1 1 1
BE⊥EC .
1
(1)证明:BE⊥平面EBC ;
1 1
30.(2019·全国·高考真题)如图,长方体ABCD–ABC D 的底面ABCD是正方形,点E在棱AA 上,
1 1 1 1 1BE⊥EC .
1
(1)证明:BE⊥平面EBC ;
1 1
31.(2018·江苏·高考真题)在平行六面体 中, , .
求证:(1) ;
(2) .
32.(2018·北京·高考真题)如图,在三棱柱ABC− 中, 平面ABC,D,E,F,G分别为 ,
AC, , 的中点,AB=BC= ,AC= =2.
(1)求证:AC⊥平面BEF;
33.(2018·北京·高考真题)如图,在四棱锥 中,底面 为矩形,平面 平面 ,
, , 、 分别为 、 的中点.(Ⅰ)求证: ;
(Ⅱ)求证:平面 平面 ;
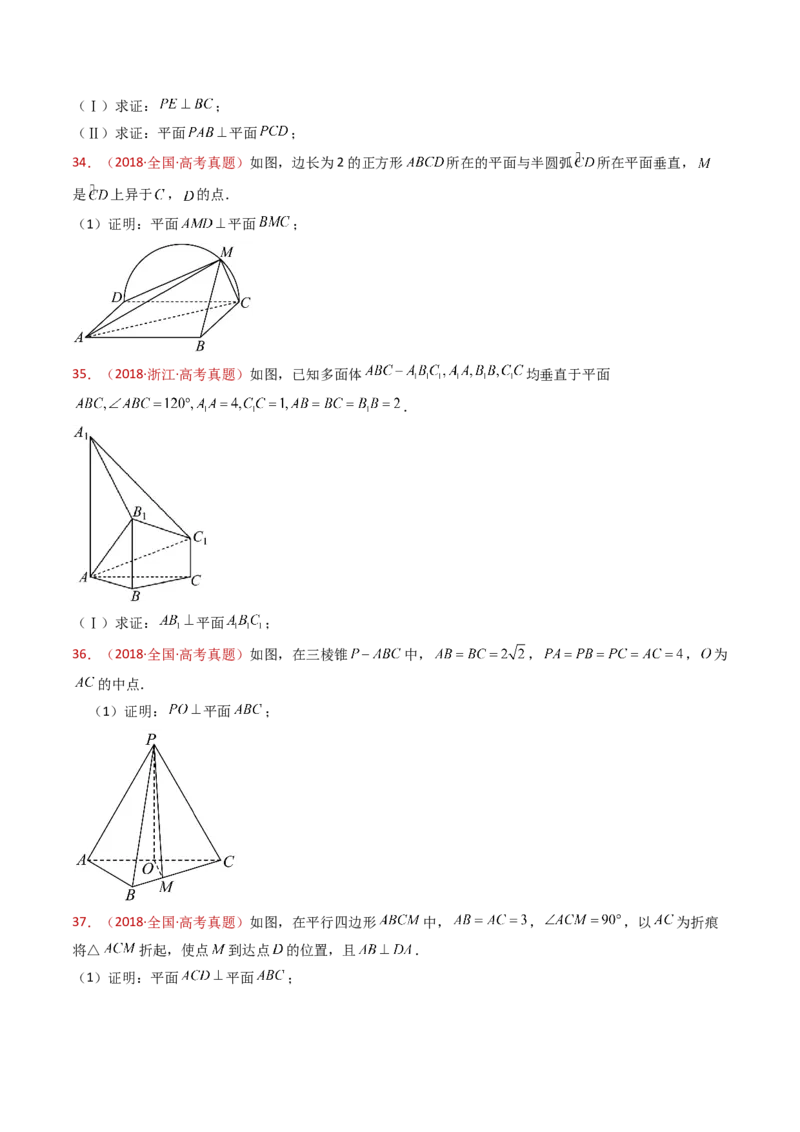
34.(2018·全国·高考真题)如图,边长为2的正方形 所在的平面与半圆弧 所在平面垂直,
是 上异于 , 的点.
(1)证明:平面 平面 ;
35.(2018·浙江·高考真题)如图,已知多面体 均垂直于平面
.
(Ⅰ)求证: 平面 ;
36.(2018·全国·高考真题)如图,在三棱锥 中, , , 为
的中点.
(1)证明: 平面 ;
37.(2018·全国·高考真题)如图,在平行四边形 中, , ,以 为折痕
将△ 折起,使点 到达点 的位置,且 .
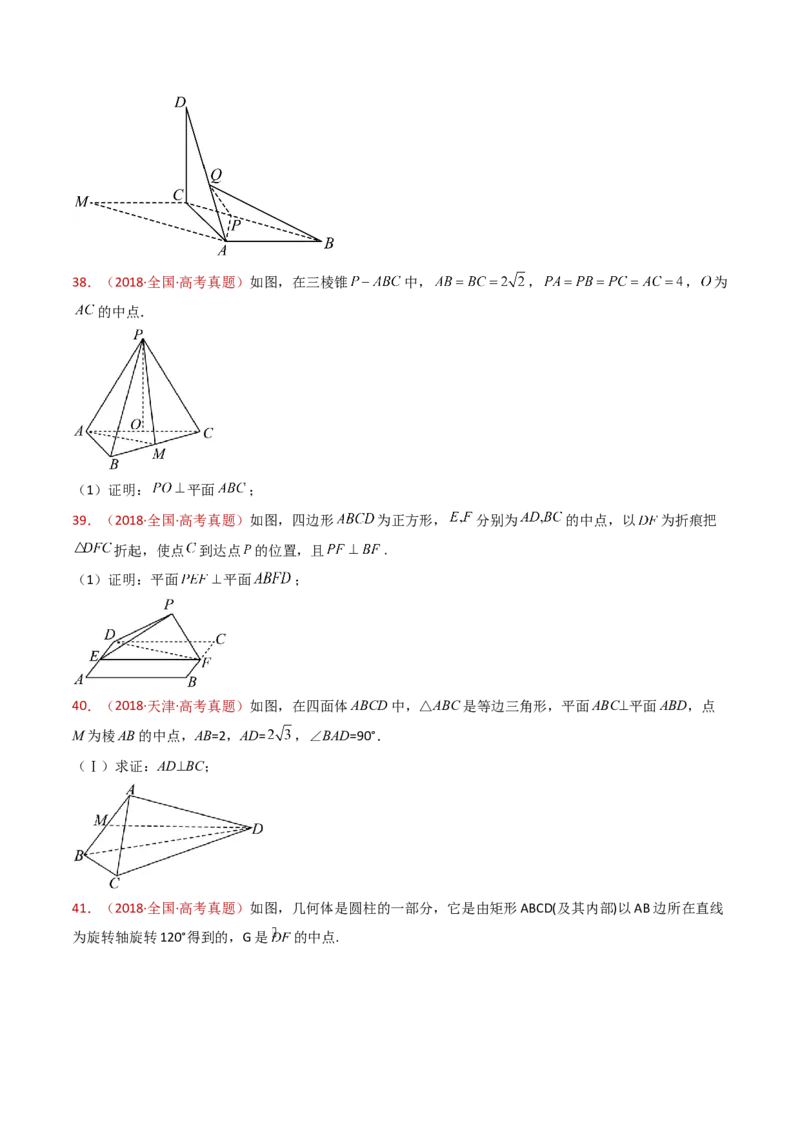
(1)证明:平面 平面 ;38.(2018·全国·高考真题)如图,在三棱锥 中, , , 为
的中点.
(1)证明: 平面 ;
39.(2018·全国·高考真题)如图,四边形 为正方形, 分别为 的中点,以 为折痕把
折起,使点 到达点 的位置,且 .
(1)证明:平面 平面 ;
40.(2018·天津·高考真题)如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点
M为棱AB的中点,AB=2,AD= ,∠BAD=90°.
(Ⅰ)求证:AD⊥BC;
41.(2018·全国·高考真题)如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线
为旋转轴旋转120°得到的,G是 的中点.(1)设P是 上的一点,且AP⊥BE,求∠CBP的大小;
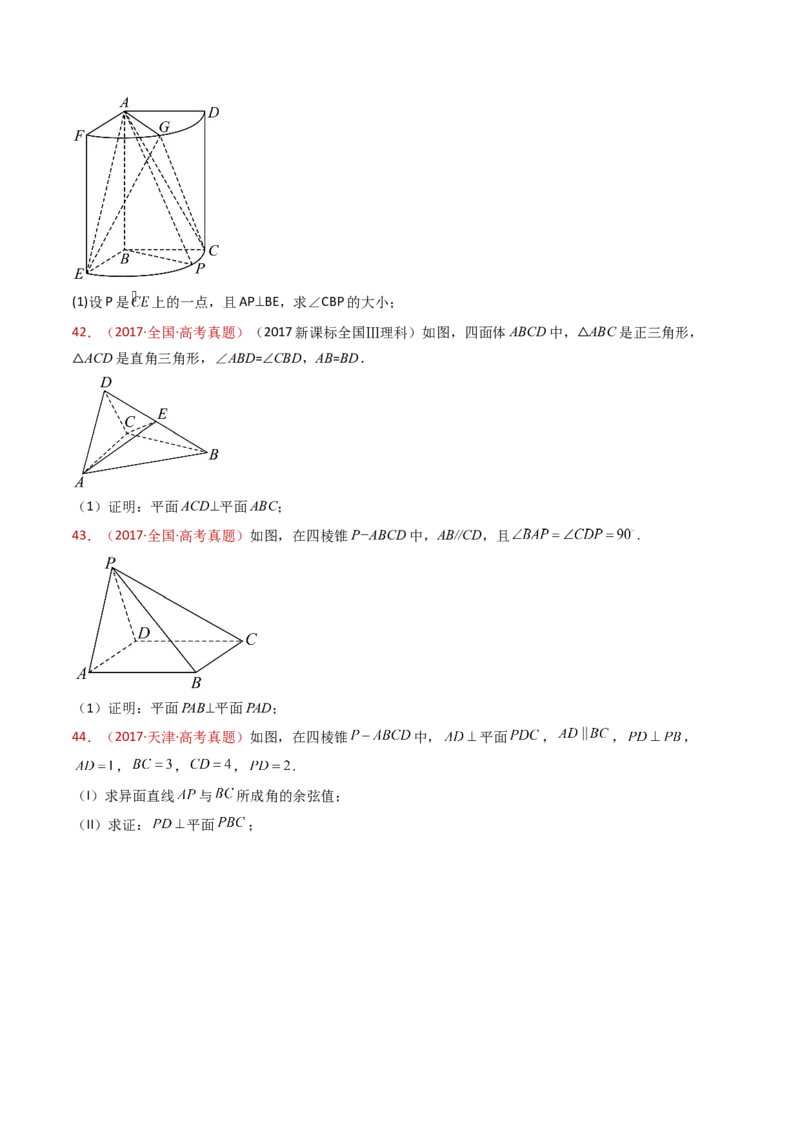
42.(2017·全国·高考真题)(2017新课标全国Ⅲ理科)如图,四面体ABCD中, ABC是正三角形,
ACD是直角三角形,∠ABD=∠CBD,AB=BD.
△
△
(1)证明:平面ACD⊥平面ABC;
43.(2017·全国·高考真题)如图,在四棱锥P−ABCD中,AB//CD,且 .
(1)证明:平面PAB⊥平面PAD;
44.(2017·天津·高考真题)如图,在四棱锥 中, 平面 , , ,
, , , .
(I)求异面直线 与 所成角的余弦值;
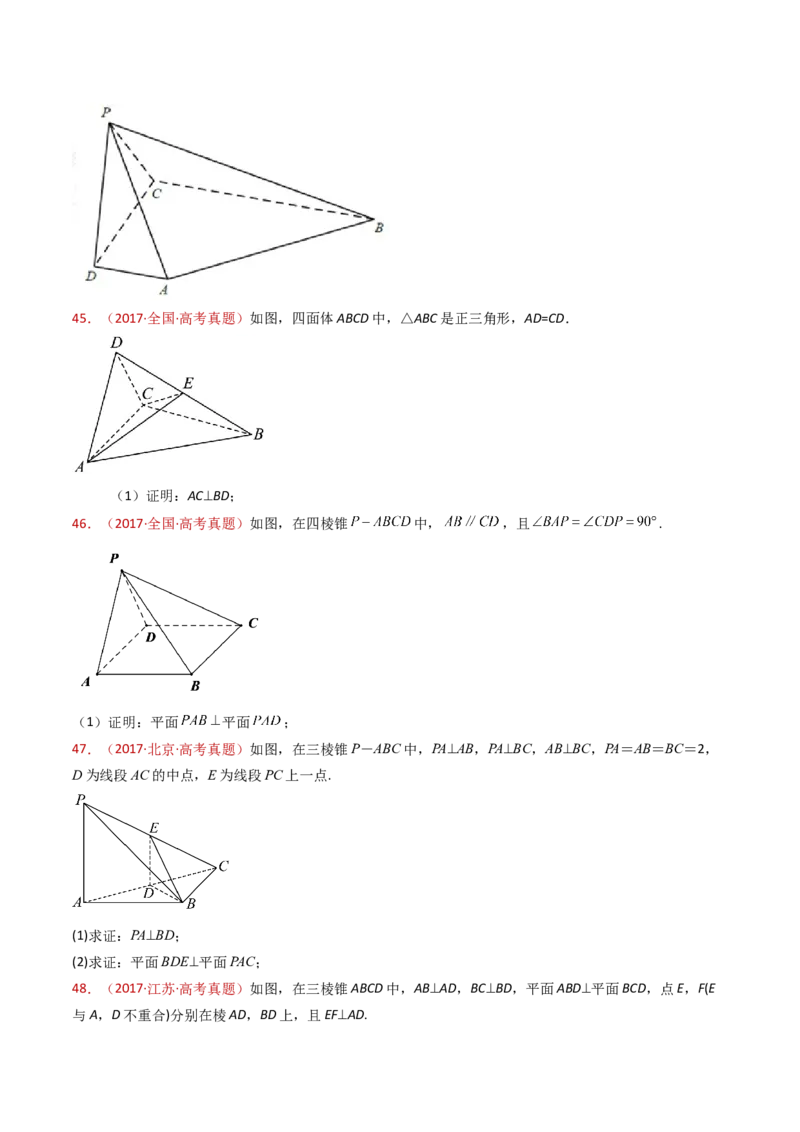
(II)求证: 平面 ;45.(2017·全国·高考真题)如图,四面体ABCD中,△ABC是正三角形,AD=CD.
(1)证明:AC⊥BD;
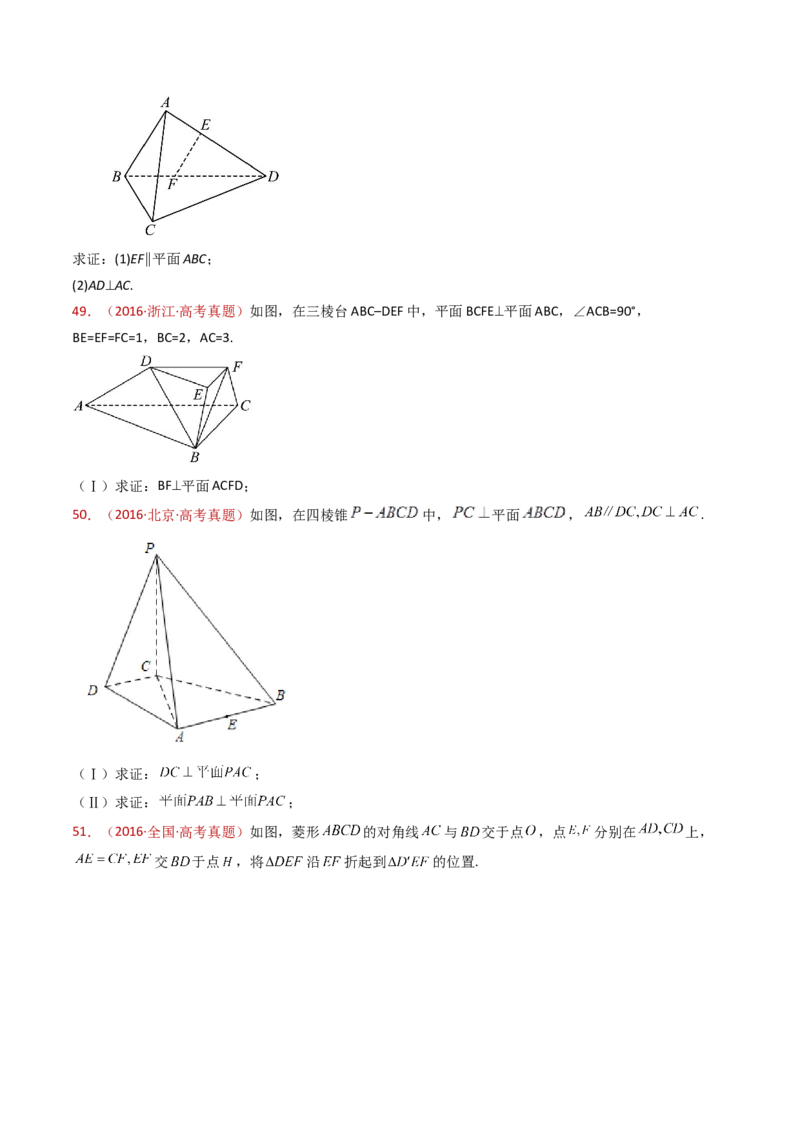
46.(2017·全国·高考真题)如图,在四棱锥 中, ,且 .
(1)证明:平面 平面 ;
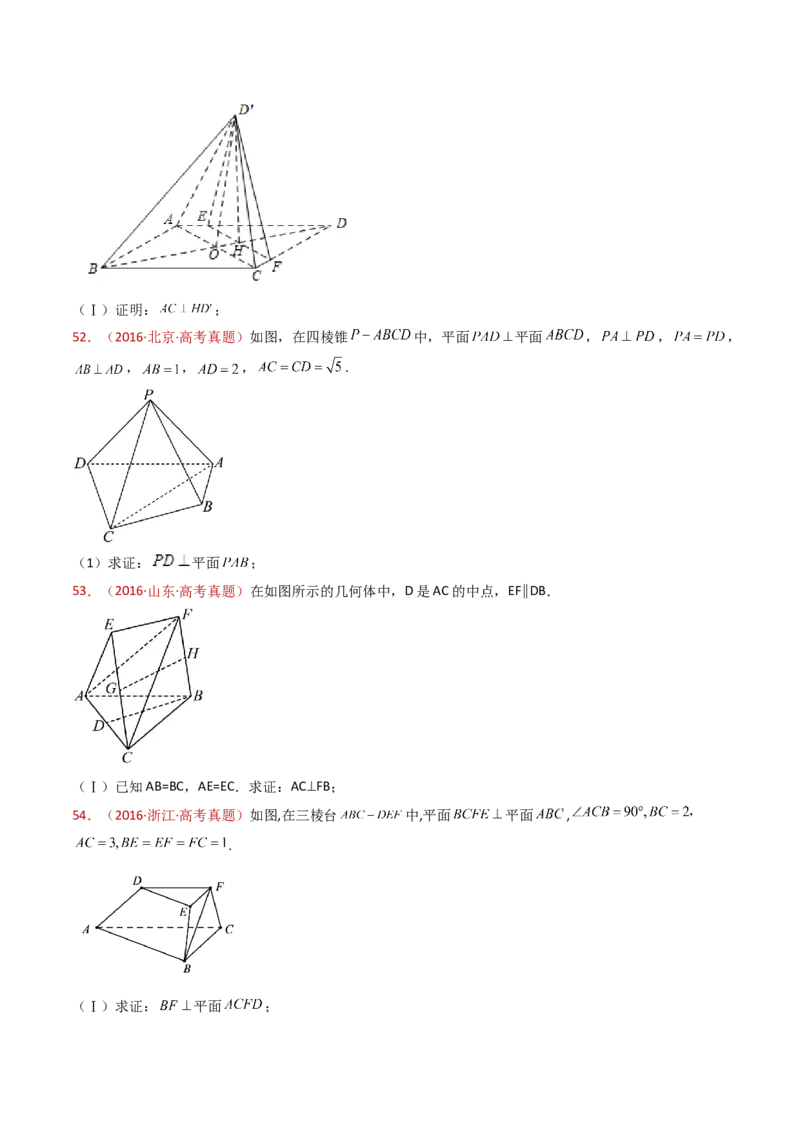
47.(2017·北京·高考真题)如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,
D为线段AC的中点,E为线段PC上一点.
(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
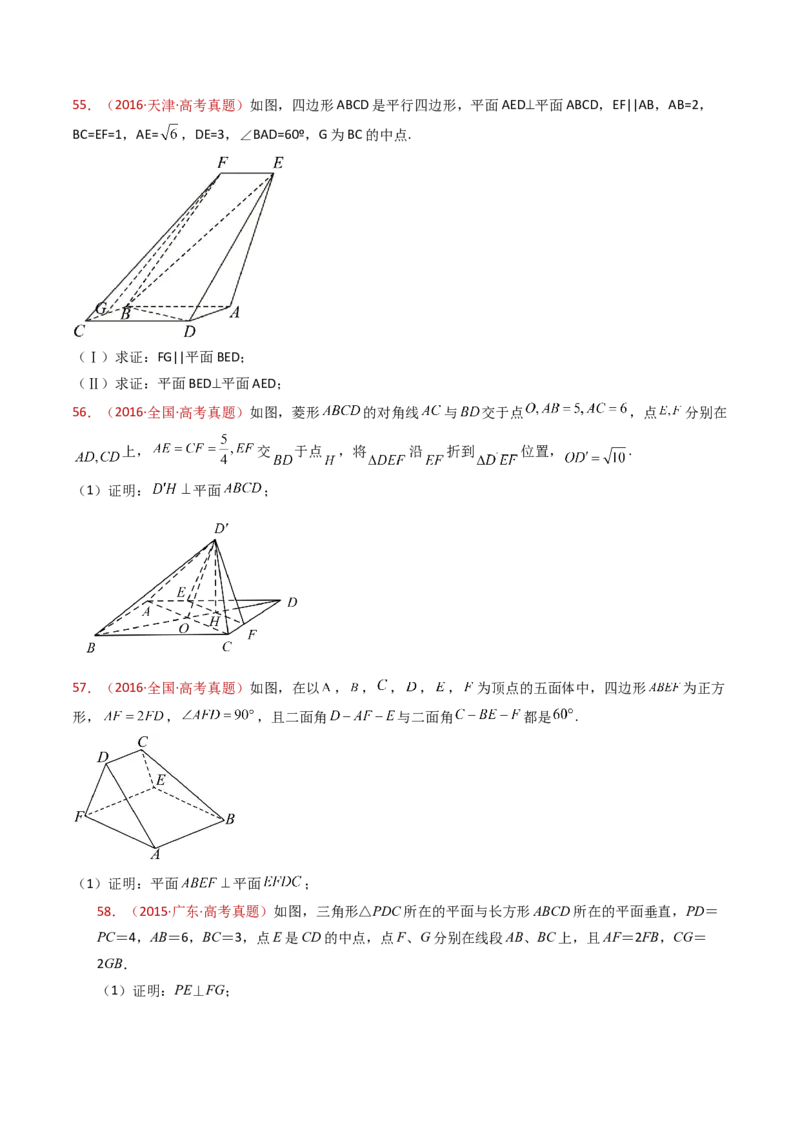
48.(2017·江苏·高考真题)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E
与A,D不重合)分别在棱AD,BD上,且EF⊥AD.求证:(1)EF∥平面ABC;
(2)AD⊥AC.
49.(2016·浙江·高考真题)如图,在三棱台ABC–DEF中,平面BCFE⊥平面ABC,∠ACB=90°,
BE=EF=FC=1,BC=2,AC=3.
(Ⅰ)求证:BF⊥平面ACFD;
50.(2016·北京·高考真题)如图,在四棱锥 中, 平面 , .
(Ⅰ)求证: ;
(Ⅱ)求证: ;
51.(2016·全国·高考真题)如图,菱形 的对角线 与 交于点 ,点 分别在 上,
交 于点 ,将 沿 折起到 的位置.(Ⅰ)证明: ;
52.(2016·北京·高考真题)如图,在四棱锥 中,平面 平面 , , ,
, , , .
(1)求证: 平面 ;
53.(2016·山东·高考真题)在如图所示的几何体中,D是AC的中点,EF∥DB.
(Ⅰ)已知AB=BC,AE=EC.求证:AC⊥FB;
54.(2016·浙江·高考真题)如图,在三棱台 中,平面 平面 ,
.
(Ⅰ)求证: 平面 ;55.(2016·天津·高考真题)如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF||AB,AB=2,
BC=EF=1,AE= ,DE=3,∠BAD=60º,G为BC的中点.
(Ⅰ)求证:FG||平面BED;
(Ⅱ)求证:平面BED⊥平面AED;
56.(2016·全国·高考真题)如图,菱形 的对角线 与 交于点 ,点 分别在
上, 交 于点 ,将 沿 折到 位置, .
(1)证明: 平面 ;
57.(2016·全国·高考真题)如图,在以 , , , , , 为顶点的五面体中,四边形 为正方
形, , ,且二面角 与二面角 都是 .
(1)证明:平面 平面 ;
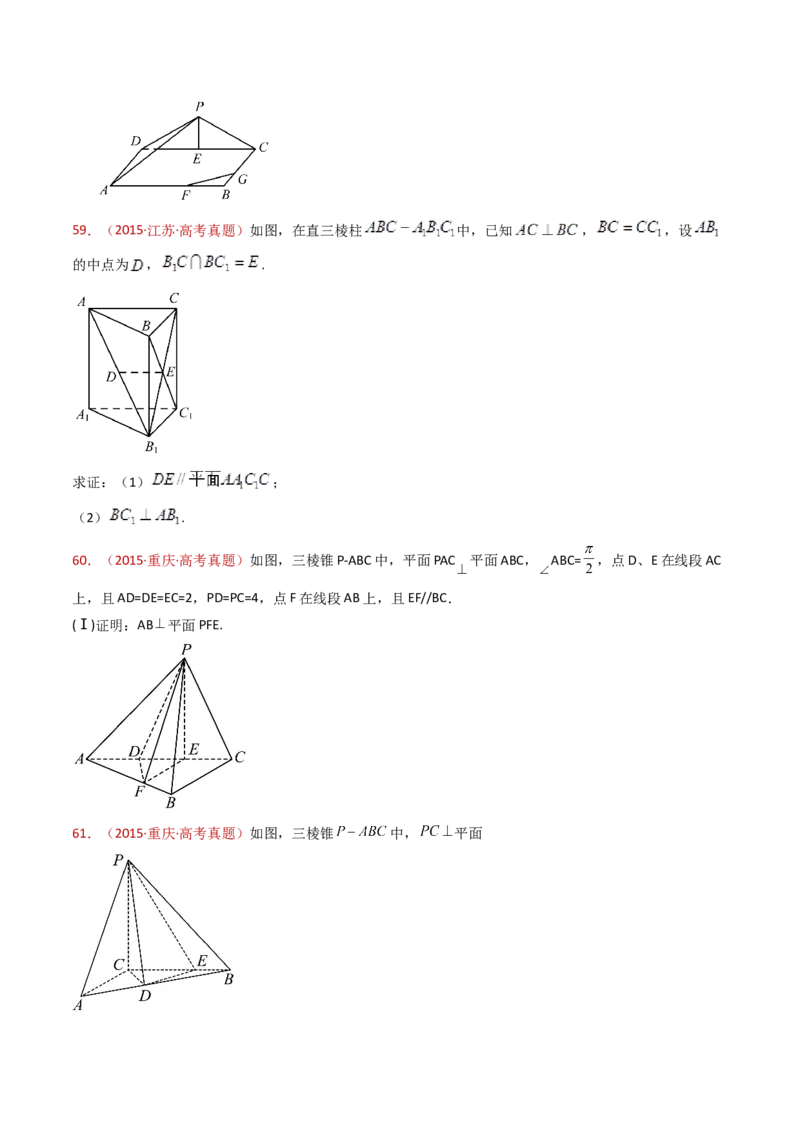
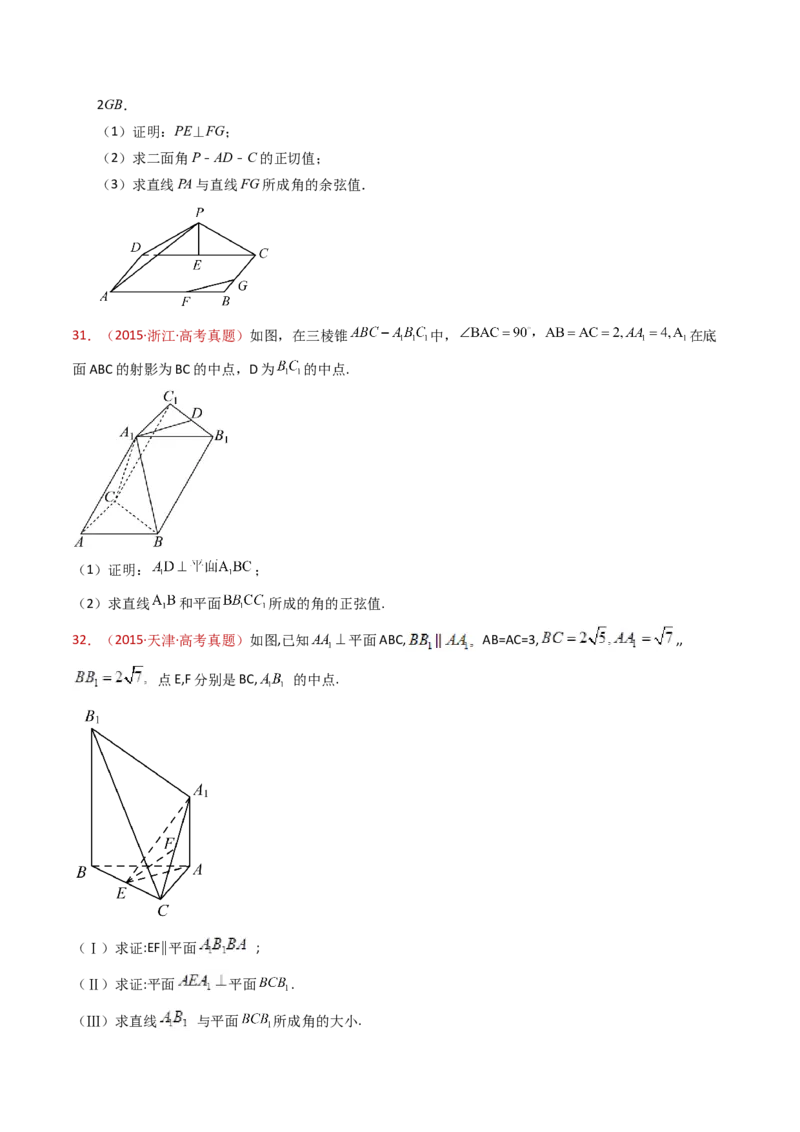
58.(2015·广东·高考真题)如图,三角形△PDC所在的平面与长方形ABCD所在的平面垂直,PD=
PC=4,AB=6,BC=3,点E是CD的中点,点F、G分别在线段AB、BC上,且AF=2FB,CG=
2GB.
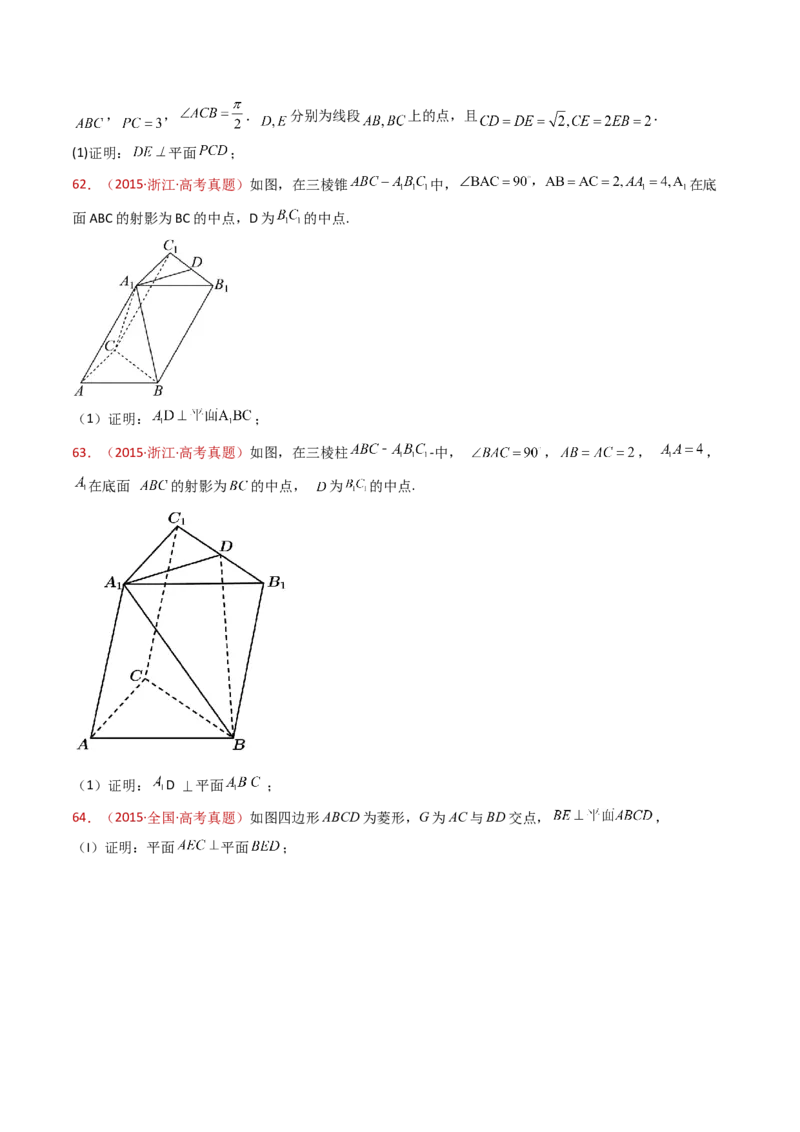
(1)证明:PE⊥FG;59.(2015·江苏·高考真题)如图,在直三棱柱 中,已知 , ,设
的中点为 , .
求证:(1) ;
(2) .
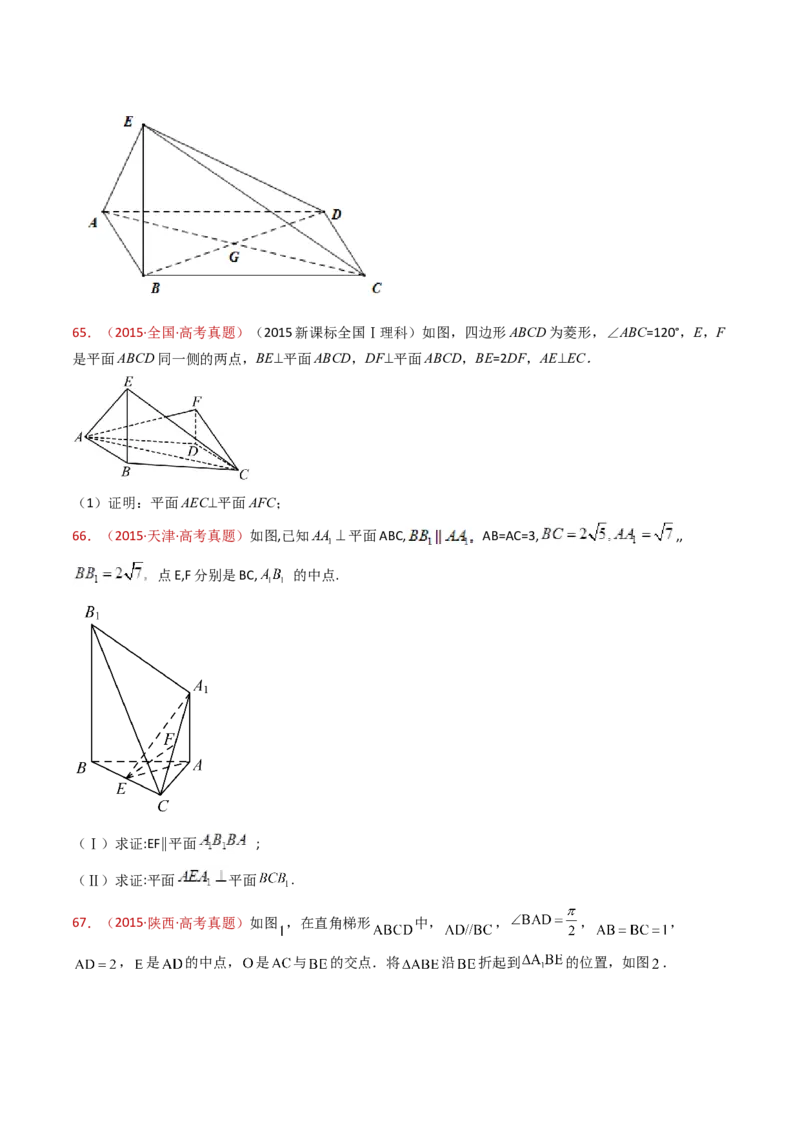
60.(2015·重庆·高考真题)如图,三棱锥P-ABC中,平面PAC 平面ABC, ABC= ,点D、E在线段AC
上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
(Ⅰ)证明:AB 平面PFE.
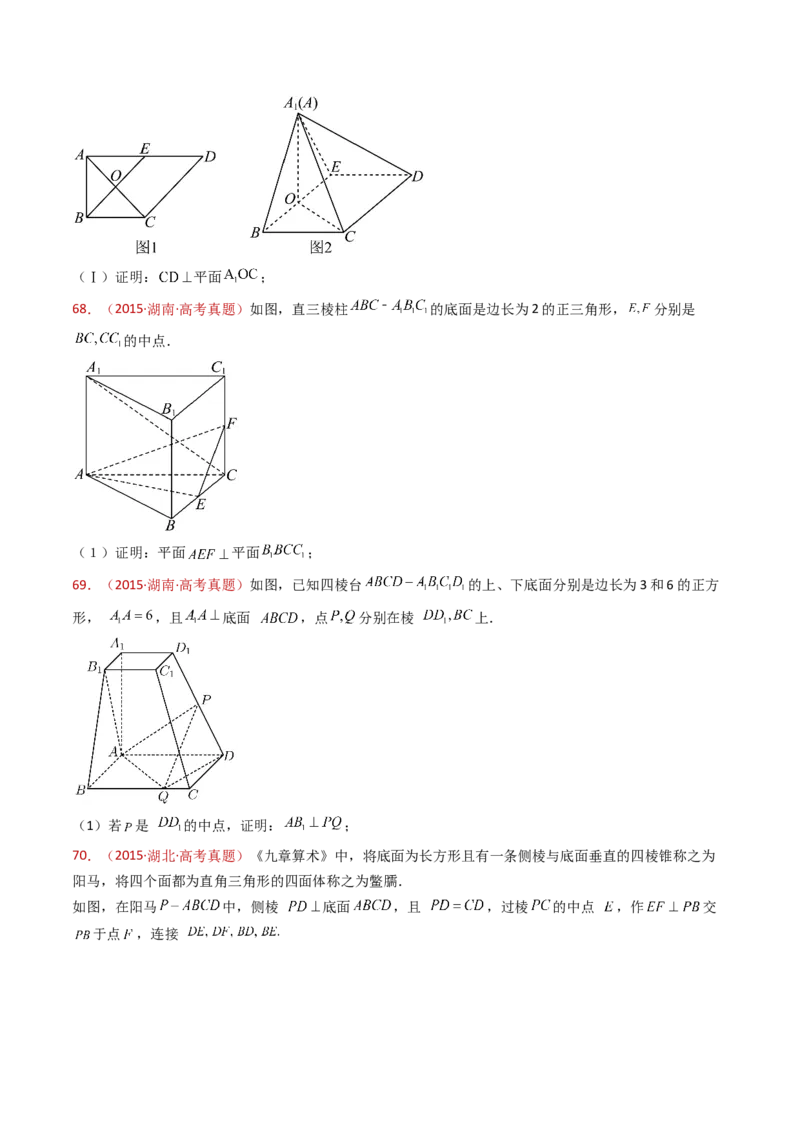
61.(2015·重庆·高考真题)如图,三棱锥 中, 平面, , . 分别为线段 上的点,且 .
(1)证明: 平面 ;
62.(2015·浙江·高考真题)如图,在三棱锥 中, 在底
面ABC的射影为BC的中点,D为 的中点.
(1)证明: ;
63.(2015·浙江·高考真题)如图,在三棱柱 -中, , , ,
在底面 的射影为 的中点, 为 的中点.
(1)证明: D 平面 ;
64.(2015·全国·高考真题)如图四边形ABCD为菱形,G为AC与BD交点, ,
(I)证明:平面 平面 ;65.(2015·全国·高考真题)(2015新课标全国Ⅰ理科)如图,四边形ABCD为菱形,∠ABC=120°,E,F
是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.
(1)证明:平面AEC⊥平面AFC;
66.(2015·天津·高考真题)如图,已知 平面ABC, AB=AC=3, ,,
点E,F分别是BC, 的中点.
(Ⅰ)求证:EF∥平面 ;
(Ⅱ)求证:平面 平面 .
67.(2015·陕西·高考真题)如图 ,在直角梯形 中, , , ,
, 是 的中点, 是 与 的交点.将 沿 折起到 的位置,如图 .(Ⅰ)证明: 平面 ;
68.(2015·湖南·高考真题)如图,直三棱柱 的底面是边长为2的正三角形, 分别是
的中点.
(1)证明:平面 平面 ;
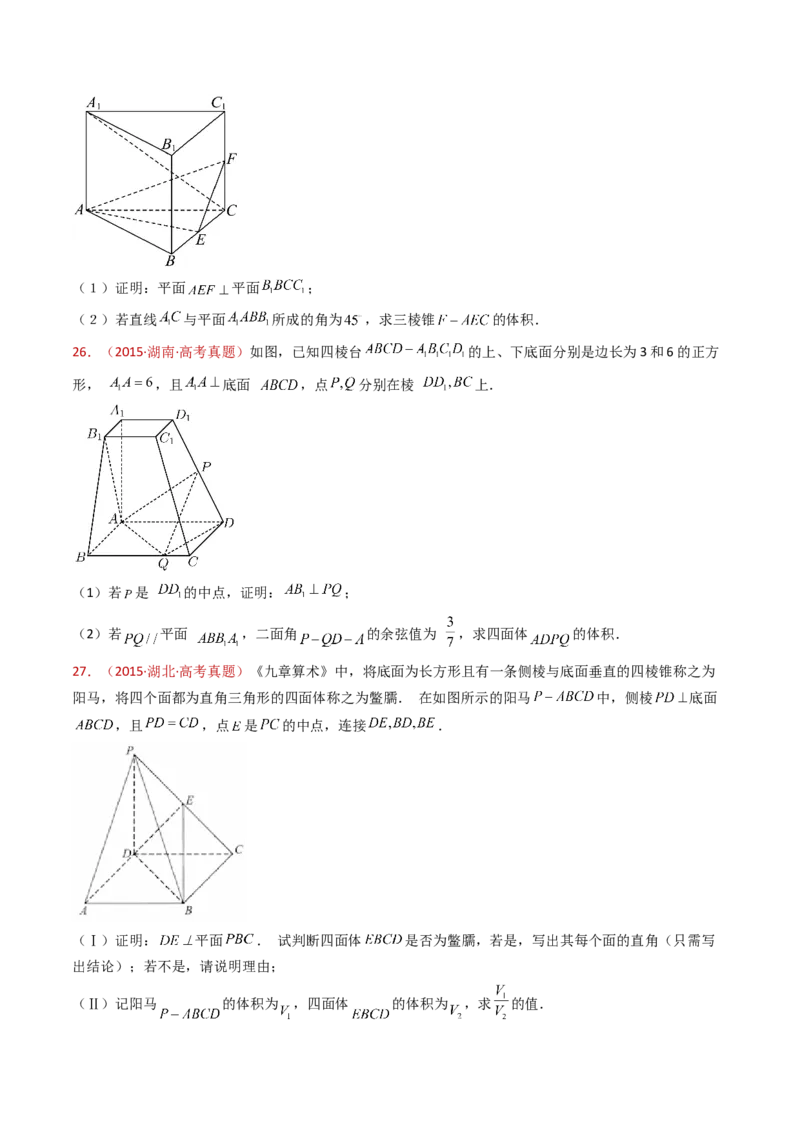
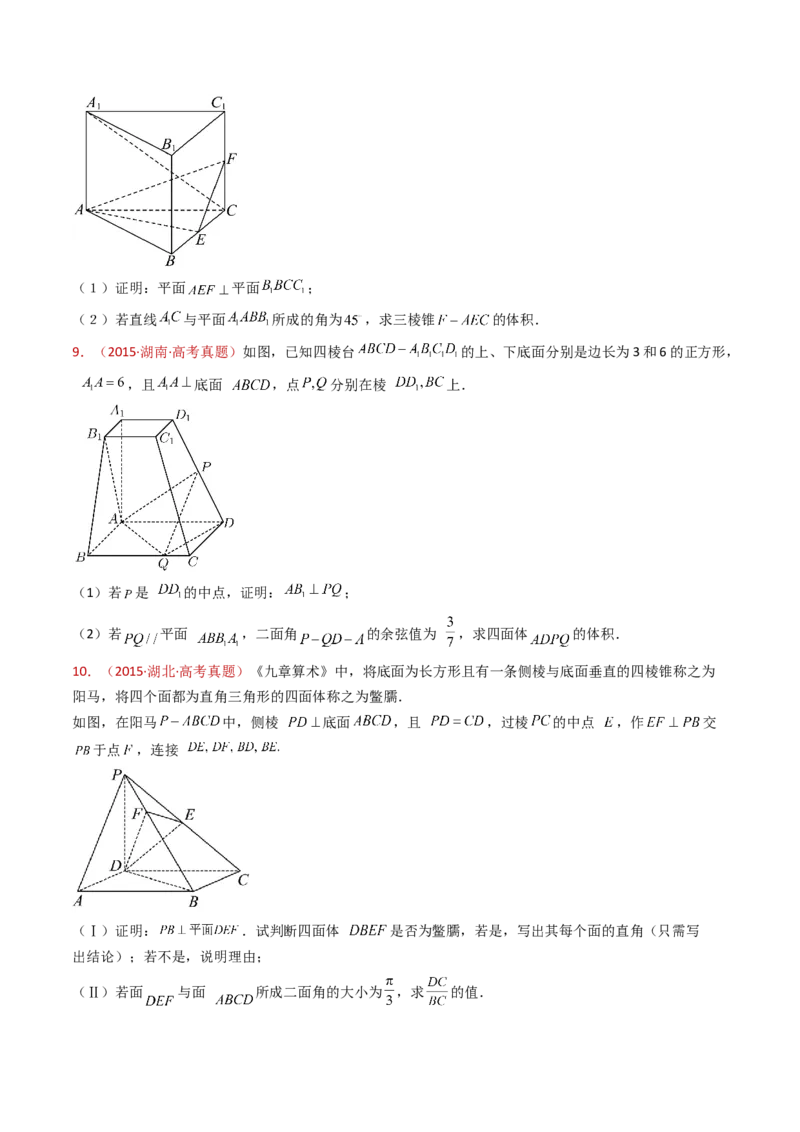
69.(2015·湖南·高考真题)如图,已知四棱台 的上、下底面分别是边长为3和6的正方
形, ,且 底面 ,点 分别在棱 上.
(1)若 是 的中点,证明: ;
70.(2015·湖北·高考真题)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为
阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马 中,侧棱 底面 ,且 ,过棱 的中点 ,作 交
于点 ,连接(Ⅰ)证明: .试判断四面体 是否为鳖臑,若是,写出其每个面的直角(只需写
出结论);若不是,说明理由;
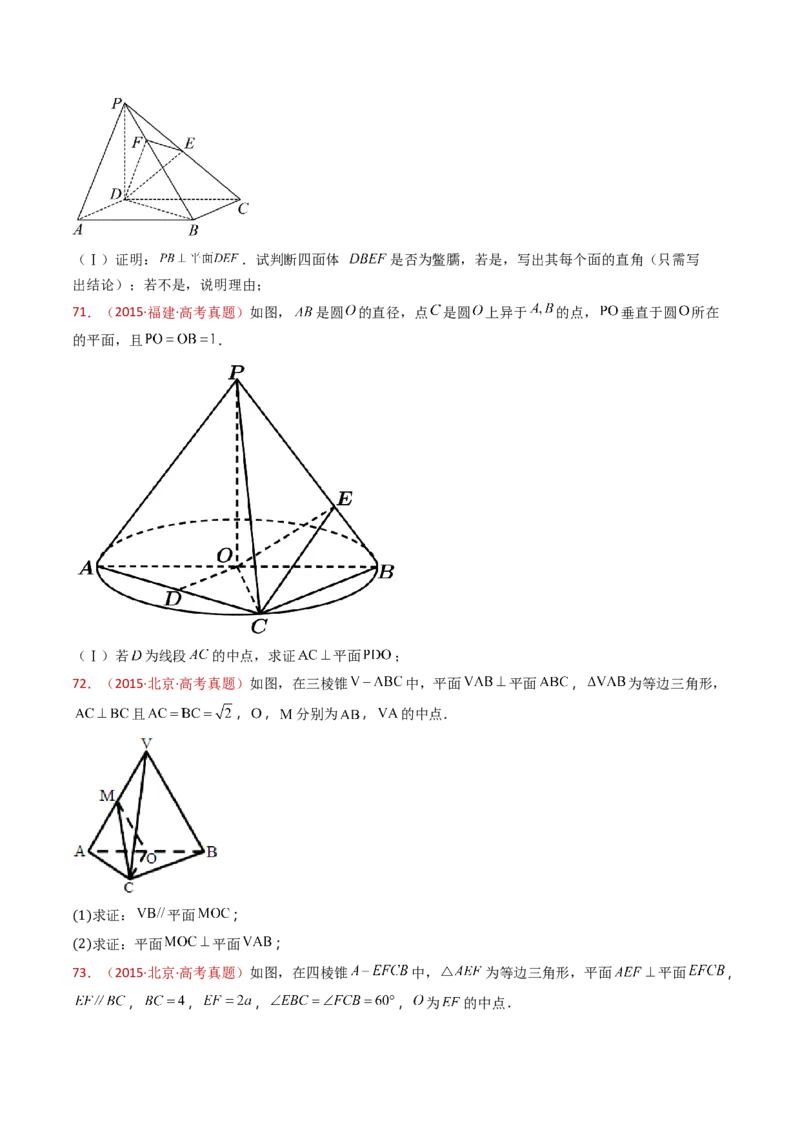
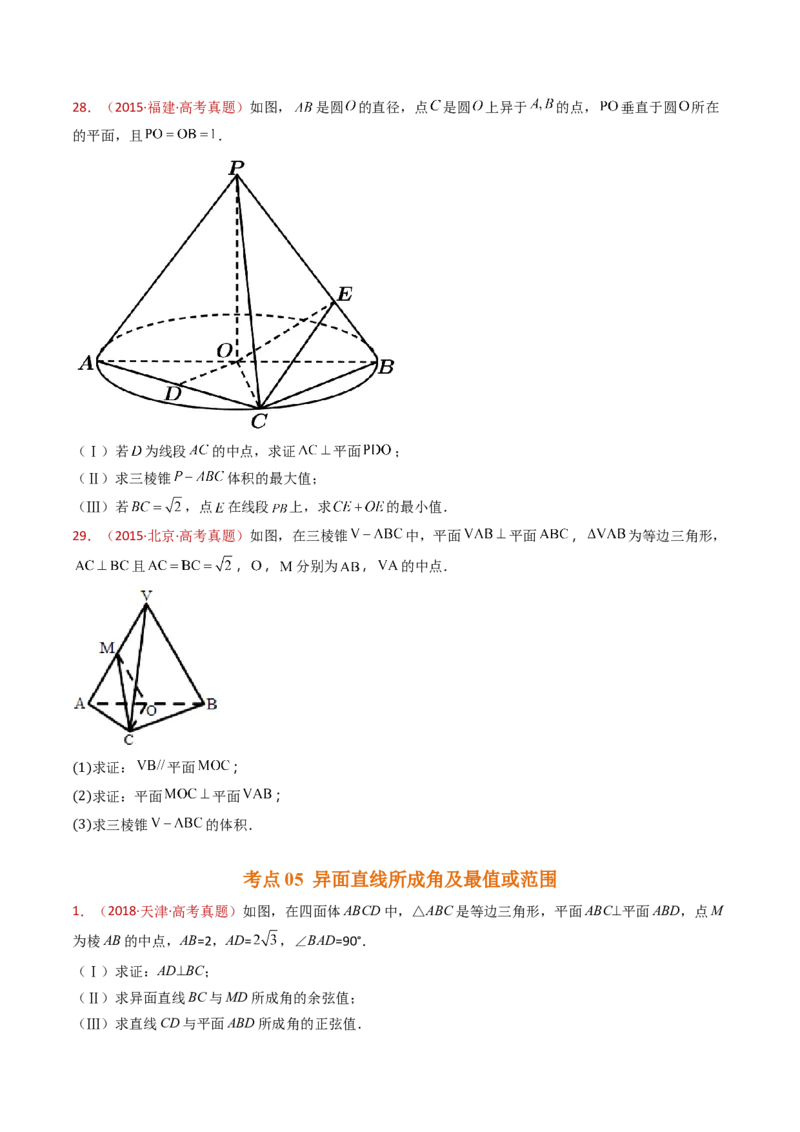
71.(2015·福建·高考真题)如图, 是圆 的直径,点 是圆 上异于 的点, 垂直于圆 所在
的平面,且 .
(Ⅰ)若 为线段 的中点,求证 平面 ;
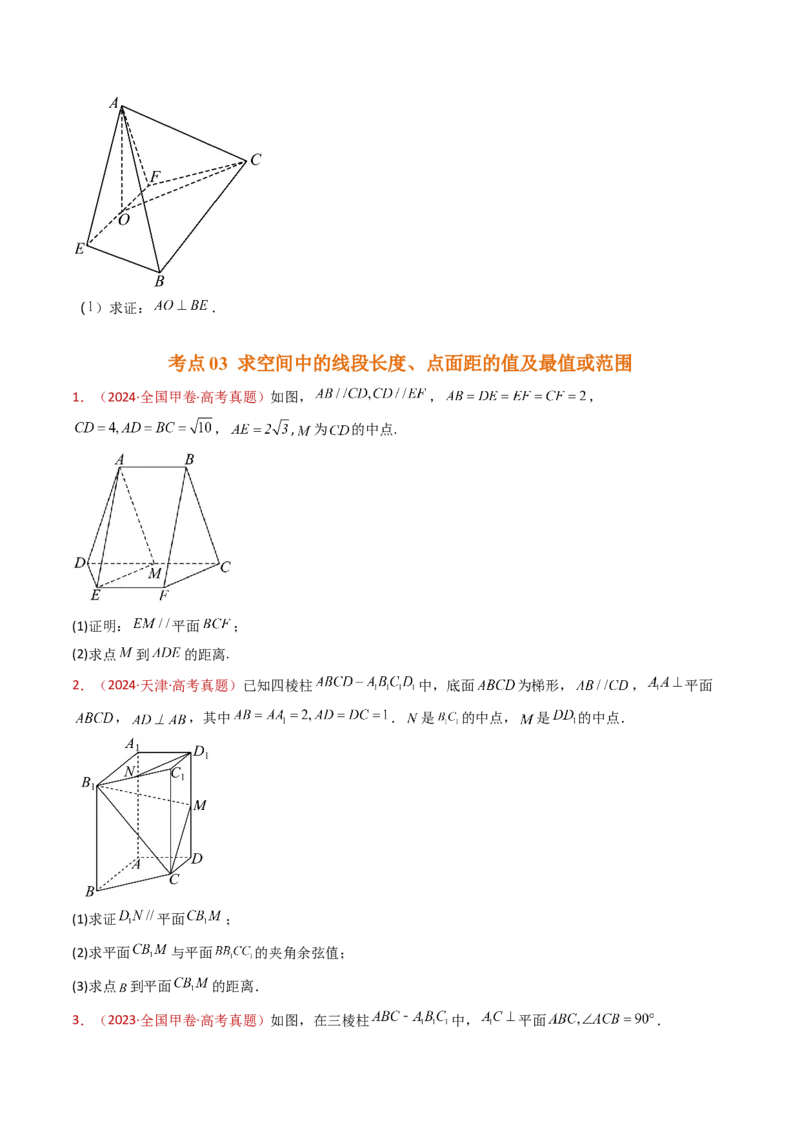
72.(2015·北京·高考真题)如图,在三棱锥 中,平面 平面 , 为等边三角形,
且 , , 分别为 , 的中点.
求证: 平面 ;
(1)求证:平面 平面 ;
(723).(2015·北京·高考真题)如图, 在四棱锥 中, 为等边三角形,平面 平面 ,
, , , , 为 的中点.( )求证: .
考点03 求空间中的线段长度、点面距的值及最值或范围
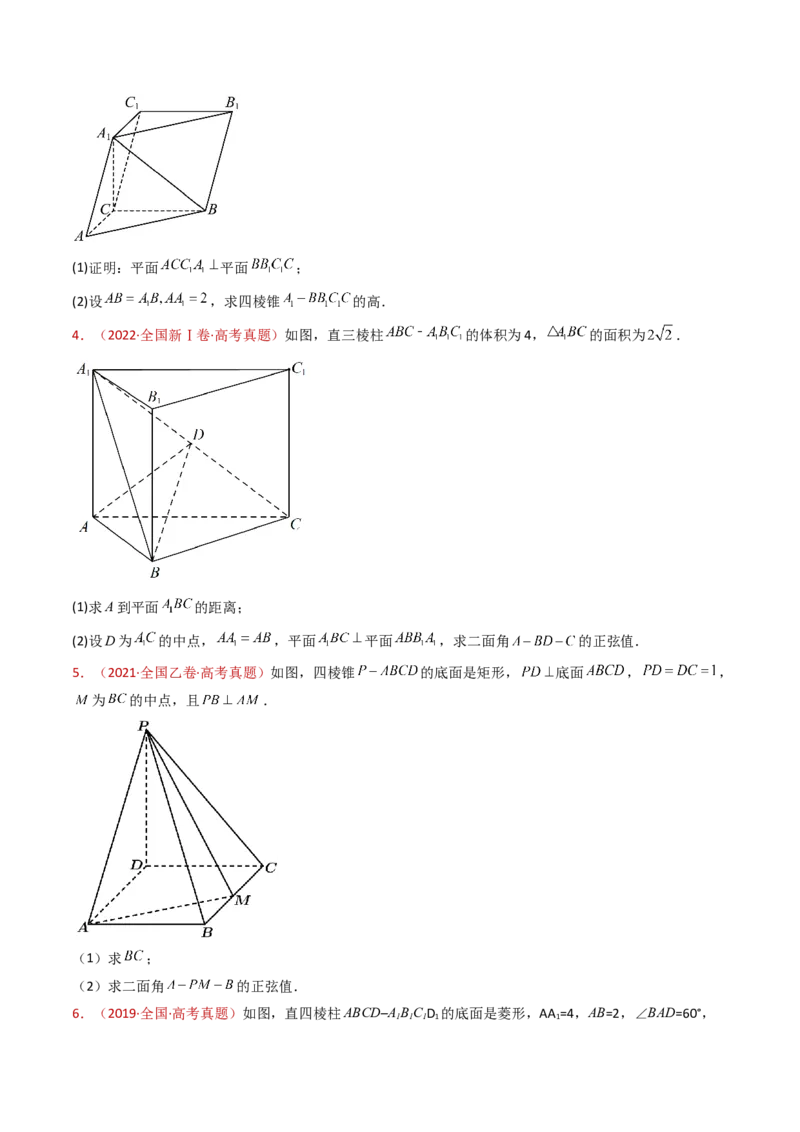
1.(2024·全国甲卷·高考真题)如图, , ,
, , 为 的中点.
(1)证明: 平面 ;
(2)求点 到 的距离.
2.(2024·天津·高考真题)已知四棱柱 中,底面 为梯形, , 平面
, ,其中 . 是 的中点, 是 的中点.
(1)求证 平面 ;
(2)求平面 与平面 的夹角余弦值;
(3)求点 到平面 的距离.
3.(2023·全国甲卷·高考真题)如图,在三棱柱 中, 平面 .(1)证明:平面 平面 ;
(2)设 ,求四棱锥 的高.
4.(2022·全国新Ⅰ卷·高考真题)如图,直三棱柱 的体积为4, 的面积为 .
(1)求A到平面 的距离;
(2)设D为 的中点, ,平面 平面 ,求二面角 的正弦值.
5.(2021·全国乙卷·高考真题)如图,四棱锥 的底面是矩形, 底面 , ,
为 的中点,且 .
(1)求 ;
(2)求二面角 的正弦值.
6.(2019·全国·高考真题)如图,直四棱柱ABCD–ABC D 的底面是菱形,AA =4,AB=2,∠BAD=60°,
1 1 1 1 1E,M,N分别是BC,BB ,A D的中点.
1 1
(1)证明:MN∥平面C DE;
1
(2)求点C到平面C DE的距离.
1
7.(2018·全国·高考真题)如图,在三棱锥 中, , , 为
的中点.
(1)证明: 平面 ;
(2)若点 在棱 上,且 ,求点 到平面 的距离.
考点04 求空间中的体积、表面积的值及最值或范围
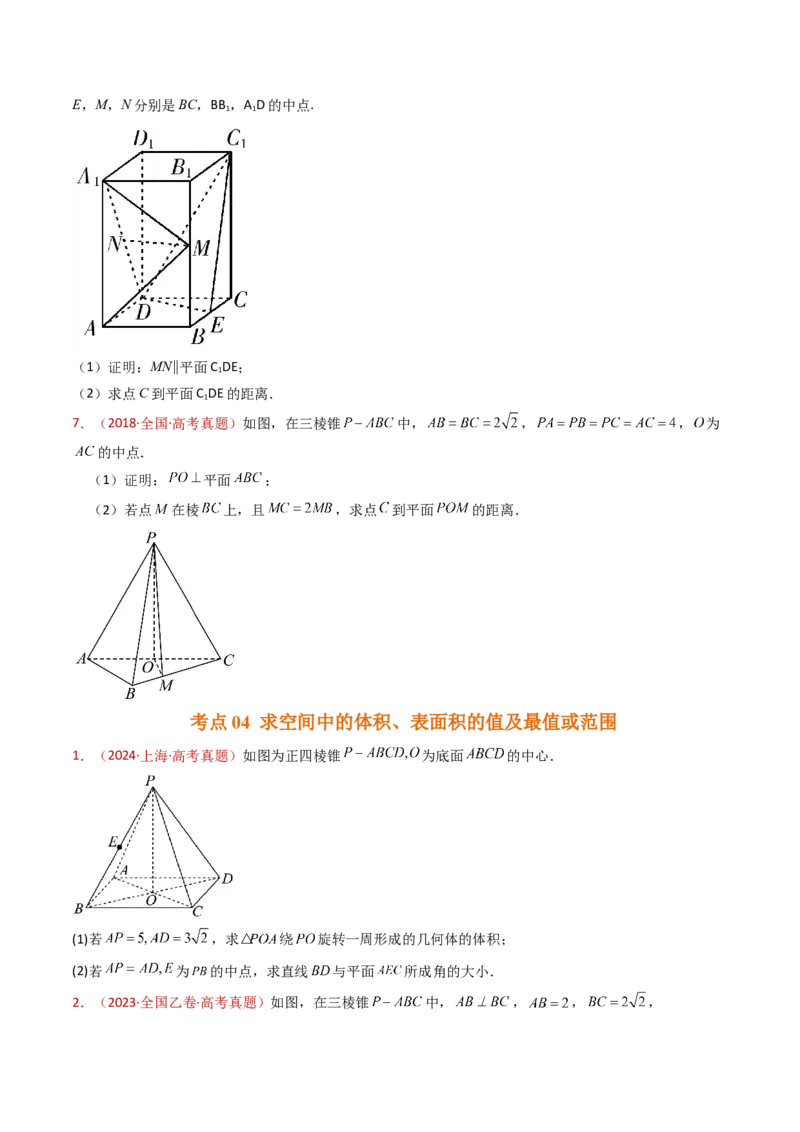
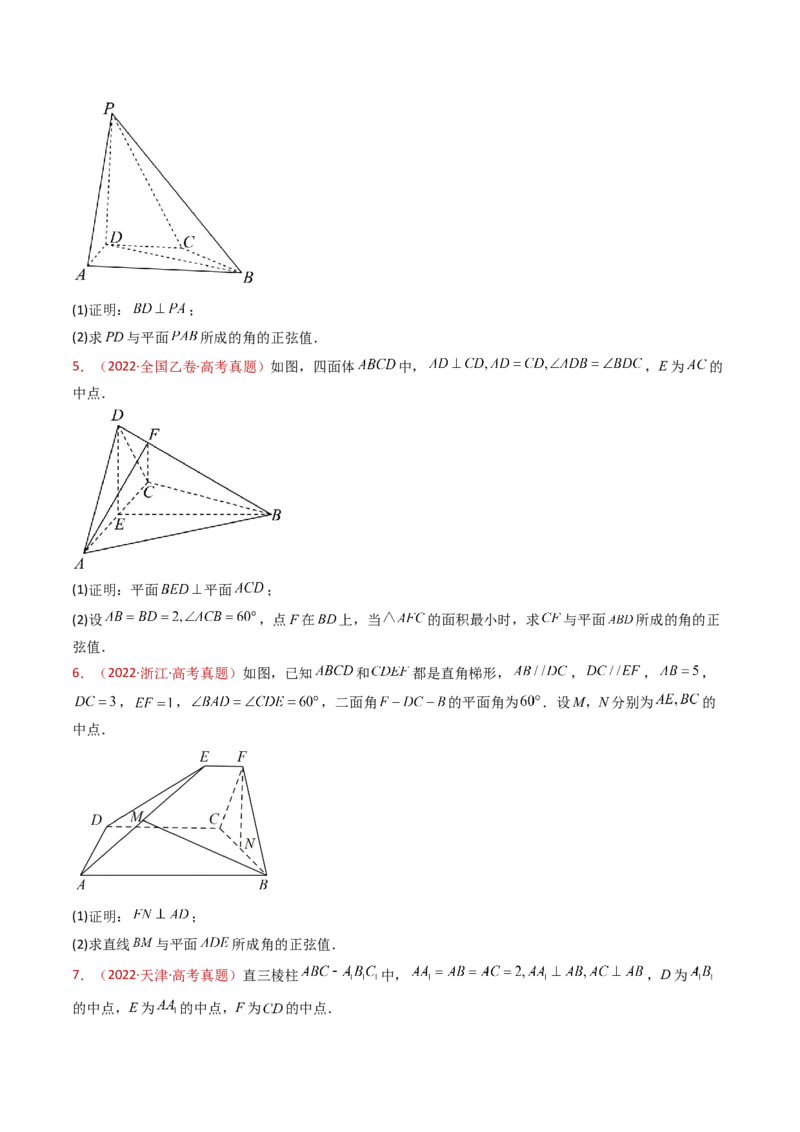
1.(2024·上海·高考真题)如图为正四棱锥 为底面 的中心.
(1)若 ,求 绕 旋转一周形成的几何体的体积;
(2)若 为 的中点,求直线 与平面 所成角的大小.
2.(2023·全国乙卷·高考真题)如图,在三棱锥 中, , , ,, 的中点分别为 ,点 在 上, .
(1)求证: //平面 ;
(2)若 ,求三棱锥 的体积.
3.(2022·全国甲卷·高考真题)小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:
底面 是边长为8(单位: )的正方形, 均为正三角形,且它们所在的
平面都与平面 垂直.
(1)证明: 平面 ;
(2)求该包装盒的容积(不计包装盒材料的厚度).
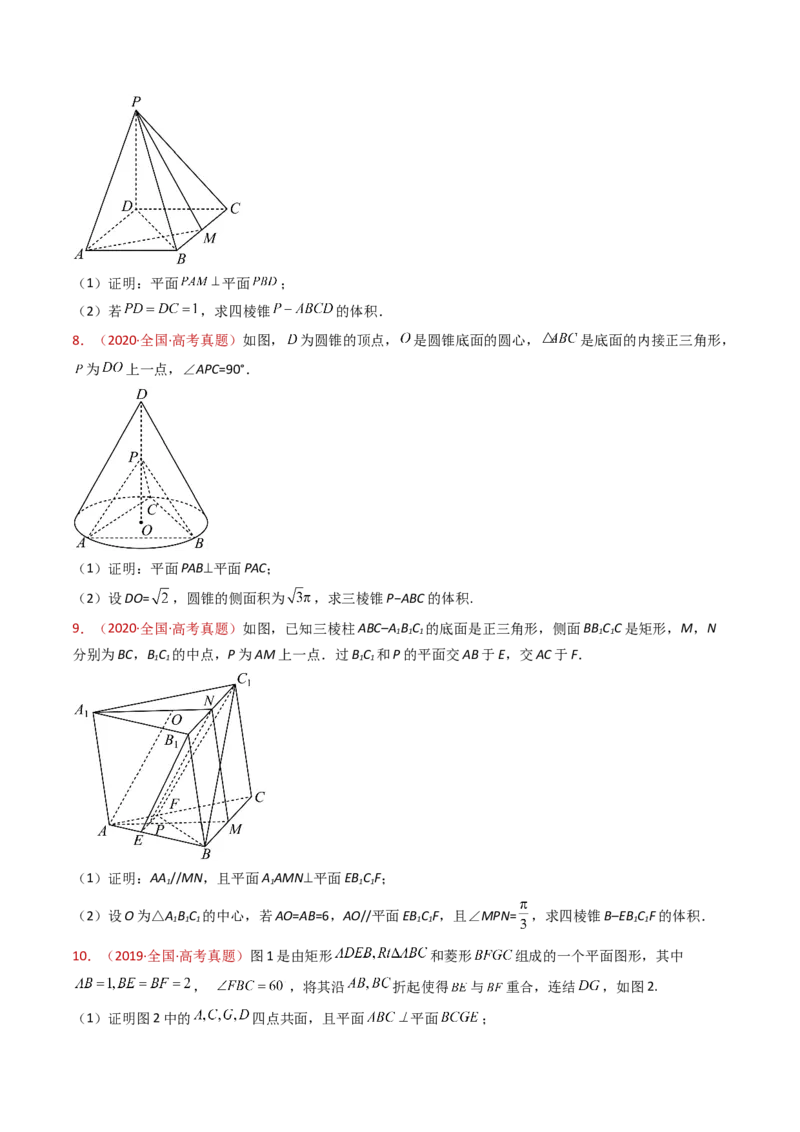
4.(2022·全国乙卷·高考真题)如图,四面体 中, ,E为AC的
中点.
(1)证明:平面 平面ACD;(2)设 ,点F在BD上,当 的面积最小时,求三棱锥 的体积.
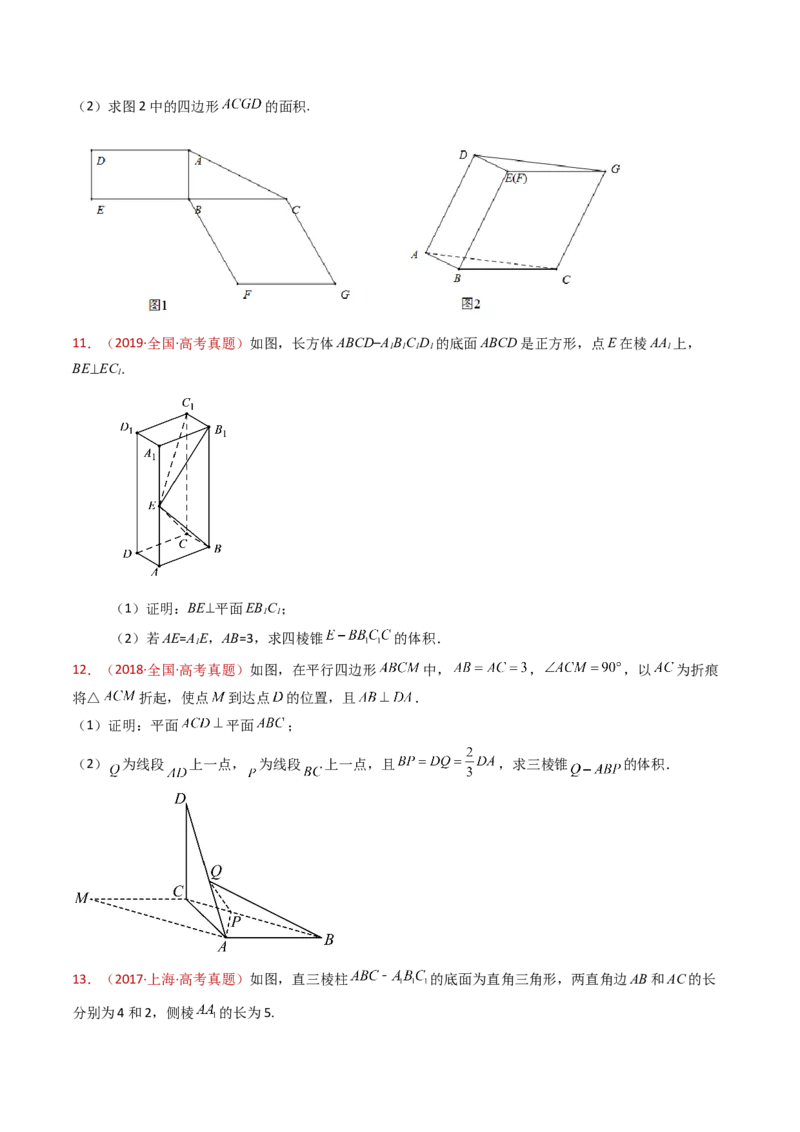
5.(2021·全国新Ⅰ卷·高考真题)如图,在三棱锥 中,平面 平面 , , 为
的中点.
(1)证明: ;
(2)若 是边长为1的等边三角形,点 在棱 上, ,且二面角 的大小为 ,
求三棱锥 的体积.
6.(2021·全国甲卷·高考真题)已知直三棱柱 中,侧面 为正方形, ,E,
F分别为 和 的中点, .
(1)求三棱锥 的体积;
(2)已知D为棱 上的点,证明: .
7.(2021·全国乙卷·高考真题)如图,四棱锥 的底面是矩形, 底面 ,M为 的中
点,且 .(1)证明:平面 平面 ;
(2)若 ,求四棱锥 的体积.
8.(2020·全国·高考真题)如图, 为圆锥的顶点, 是圆锥底面的圆心, 是底面的内接正三角形,
为 上一点,∠APC=90°.
(1)证明:平面PAB⊥平面PAC;
(2)设DO= ,圆锥的侧面积为 ,求三棱锥P−ABC的体积.
9.(2020·全国·高考真题)如图,已知三棱柱ABC–A B C 的底面是正三角形,侧面BB C C是矩形,M,N
1 1 1 1 1
分别为BC,B C 的中点,P为AM上一点.过B C 和P的平面交AB于E,交AC于F.
1 1 1 1
(1)证明:AA //MN,且平面A AMN⊥平面EB C F;
1 1 1 1
(2)设O为△A B C 的中心,若AO=AB=6,AO//平面EB C F,且∠MPN= ,求四棱锥B–EB C F的体积.
1 1 1 1 1 1 1
10.(2019·全国·高考真题)图1是由矩形 和菱形 组成的一个平面图形,其中
, ,将其沿 折起使得 与 重合,连结 ,如图2.
(1)证明图2中的 四点共面,且平面 平面 ;(2)求图2中的四边形 的面积.
11.(2019·全国·高考真题)如图,长方体ABCD–ABC D 的底面ABCD是正方形,点E在棱AA 上,
1 1 1 1 1
BE⊥EC .
1
(1)证明:BE⊥平面EBC ;
1 1
(2)若AE=AE,AB=3,求四棱锥 的体积.
1
12.(2018·全国·高考真题)如图,在平行四边形 中, , ,以 为折痕
将△ 折起,使点 到达点 的位置,且 .
(1)证明:平面 平面 ;
(2) 为线段 上一点, 为线段 上一点,且 ,求三棱锥 的体积.
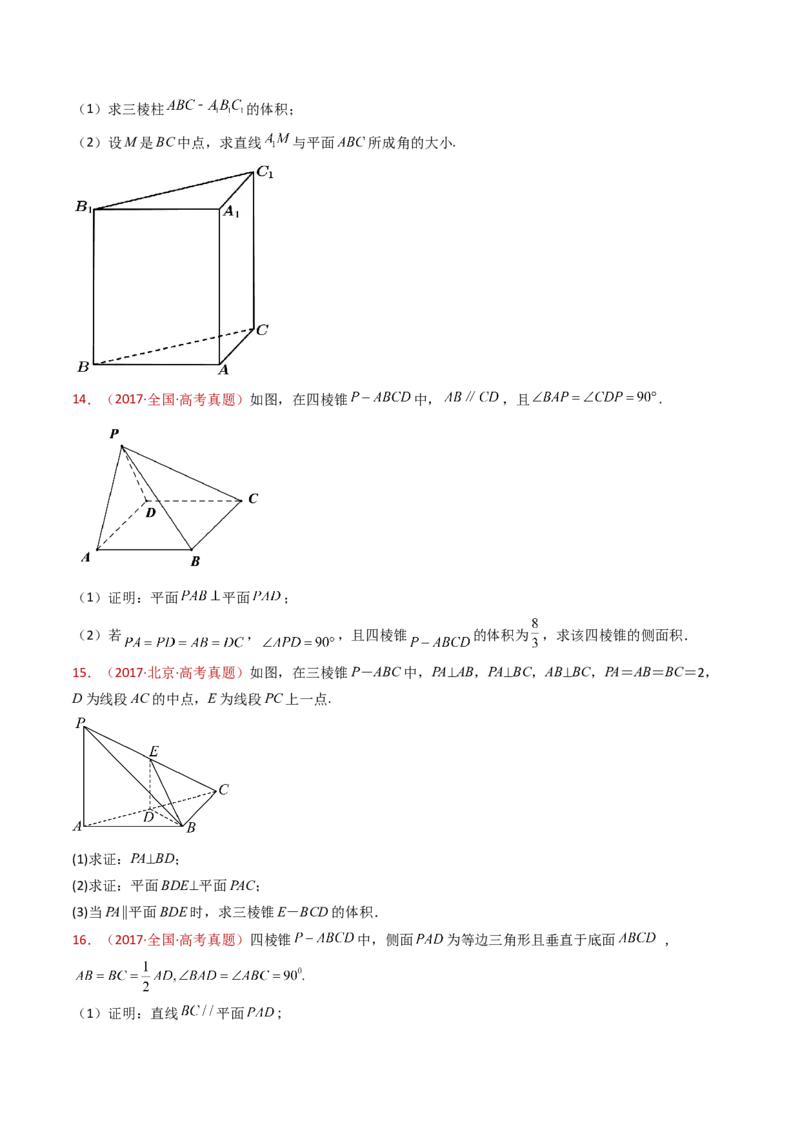
13.(2017·上海·高考真题)如图,直三棱柱 的底面为直角三角形,两直角边AB和AC的长
分别为4和2,侧棱 的长为5.(1)求三棱柱 的体积;
(2)设M是BC中点,求直线 与平面 所成角的大小.
14.(2017·全国·高考真题)如图,在四棱锥 中, ,且 .
(1)证明:平面 平面 ;
(2)若 , ,且四棱锥 的体积为 ,求该四棱锥的侧面积.
15.(2017·北京·高考真题)如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,
D为线段AC的中点,E为线段PC上一点.
(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
16.(2017·全国·高考真题)四棱锥 中,侧面 为等边三角形且垂直于底面 ,
(1)证明:直线 平面 ;(2)若△ 面积为 ,求四棱锥 的体积.
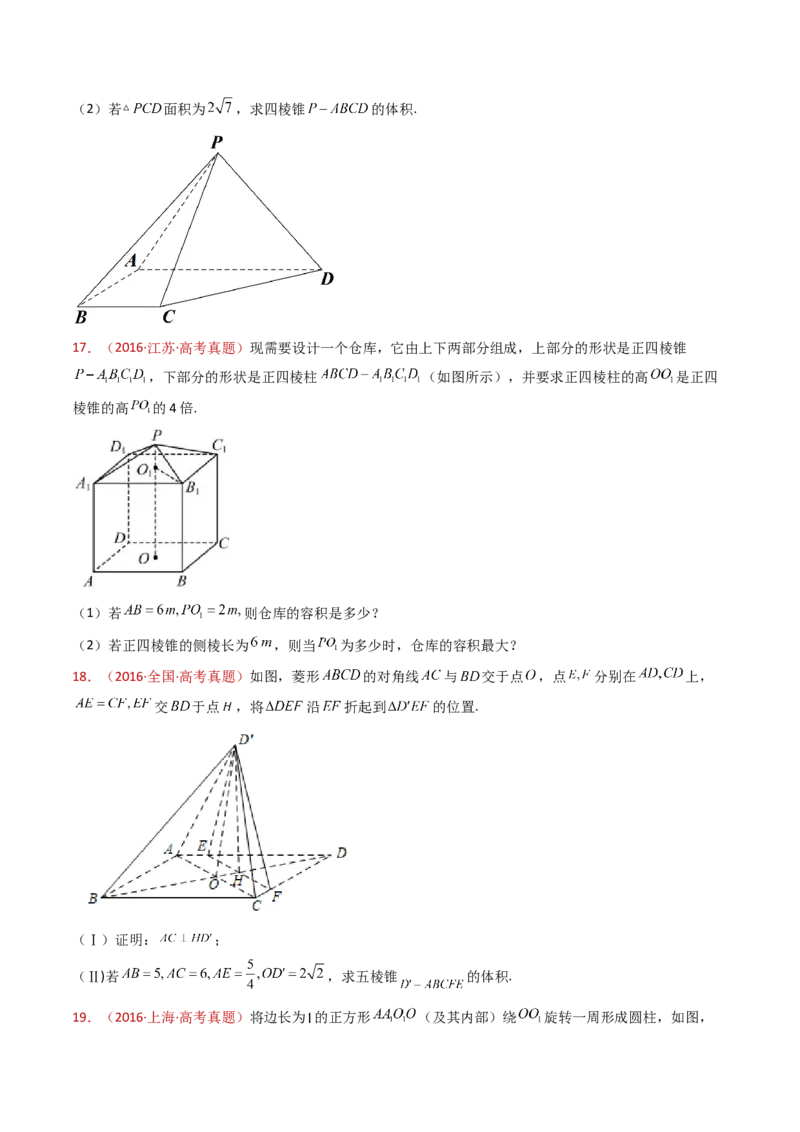
17.(2016·江苏·高考真题)现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥
,下部分的形状是正四棱柱 (如图所示),并要求正四棱柱的高 是正四
棱锥的高 的4倍.
(1)若 则仓库的容积是多少?
(2)若正四棱锥的侧棱长为 ,则当 为多少时,仓库的容积最大?
18.(2016·全国·高考真题)如图,菱形 的对角线 与 交于点 ,点 分别在 上,
交 于点 ,将 沿 折起到 的位置.
(Ⅰ)证明: ;
(Ⅱ)若 ,求五棱锥 的体积.
19.(2016·上海·高考真题)将边长为 的正方形 (及其内部)绕 旋转一周形成圆柱,如图,长为 , 长为 ,其中 与 在平面 的同侧.
(1)求三棱锥 的体积;
(2)求异面直线 与 所成的角的大小.
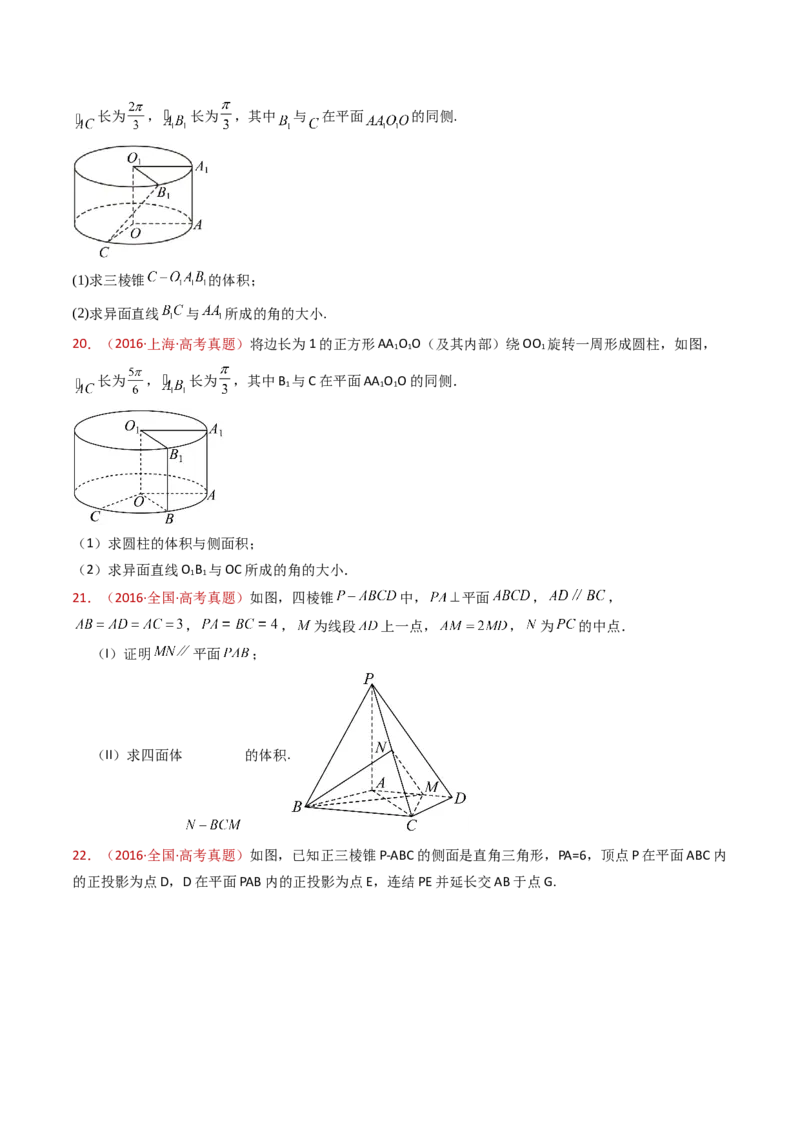
20.(2016·上海·高考真题)将边长为1的正方形AA O O(及其内部)绕OO 旋转一周形成圆柱,如图,
1 1 1
长为 , 长为 ,其中B 与C在平面AA O O的同侧.
1 1 1
(1)求圆柱的体积与侧面积;
(2)求异面直线O B 与OC所成的角的大小.
1 1
21.(2016·全国·高考真题)如图,四棱锥 中, 平面 , ,
, , 为线段 上一点, , 为 的中点.
(I)证明 平面 ;
(II)求四面体 的体积.
22.(2016·全国·高考真题)如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内
的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于点G.(Ⅰ)证明:G是AB的中点;
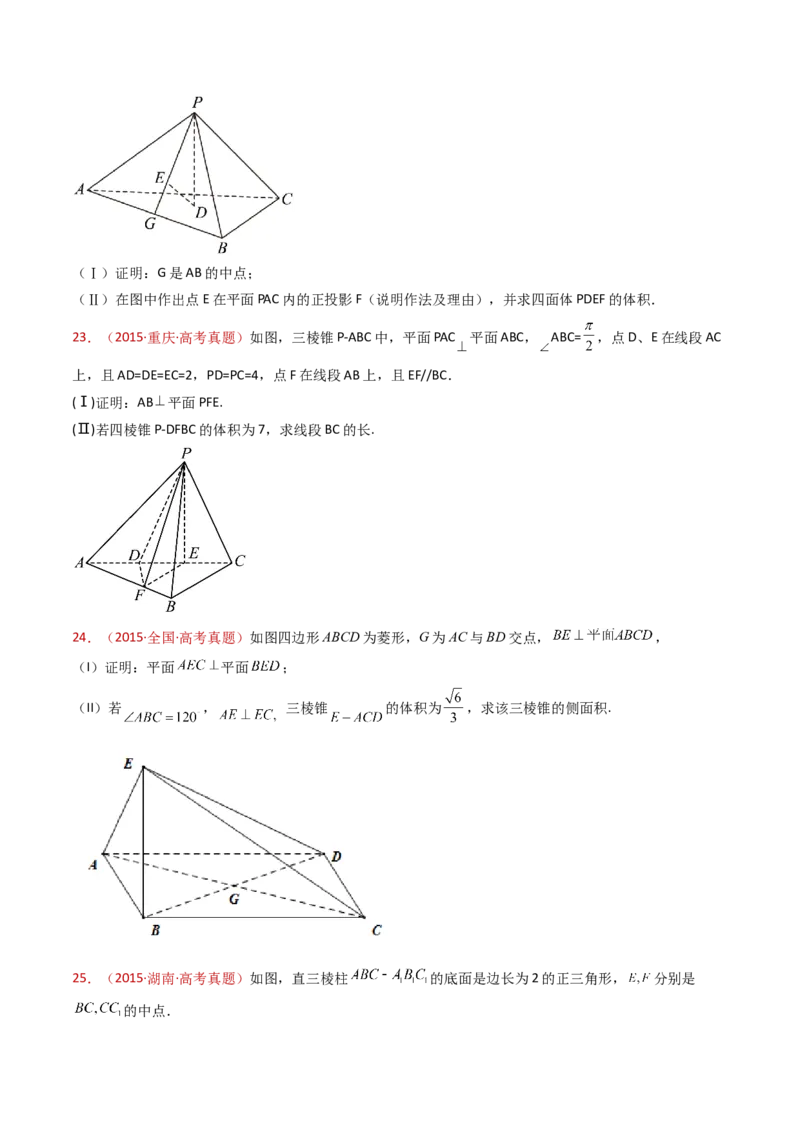
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
23.(2015·重庆·高考真题)如图,三棱锥P-ABC中,平面PAC 平面ABC, ABC= ,点D、E在线段AC
上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
(Ⅰ)证明:AB 平面PFE.
(Ⅱ)若四棱锥P-DFBC的体积为7,求线段BC的长.
24.(2015·全国·高考真题)如图四边形ABCD为菱形,G为AC与BD交点, ,
(I)证明:平面 平面 ;
(II)若 , 三棱锥 的体积为 ,求该三棱锥的侧面积.
25.(2015·湖南·高考真题)如图,直三棱柱 的底面是边长为2的正三角形, 分别是
的中点.(1)证明:平面 平面 ;
(2)若直线 与平面 所成的角为 ,求三棱锥 的体积.
26.(2015·湖南·高考真题)如图,已知四棱台 的上、下底面分别是边长为3和6的正方
形, ,且 底面 ,点 分别在棱 上.
(1)若 是 的中点,证明: ;
(2)若 平面 ,二面角 的余弦值为 ,求四面体 的体积.
27.(2015·湖北·高考真题)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为
阳马,将四个面都为直角三角形的四面体称之为鳖臑. 在如图所示的阳马 中,侧棱 底面
,且 ,点 是 的中点,连接 .
(Ⅰ)证明: 平面 . 试判断四面体 是否为鳖臑,若是,写出其每个面的直角(只需写
出结论);若不是,请说明理由;
(Ⅱ)记阳马 的体积为 ,四面体 的体积为 ,求 的值.28.(2015·福建·高考真题)如图, 是圆 的直径,点 是圆 上异于 的点, 垂直于圆 所在
的平面,且 .
(Ⅰ)若 为线段 的中点,求证 平面 ;
(Ⅱ)求三棱锥 体积的最大值;
(Ⅲ)若 ,点 在线段 上,求 的最小值.
29.(2015·北京·高考真题)如图,在三棱锥 中,平面 平面 , 为等边三角形,
且 , , 分别为 , 的中点.
求证: 平面 ;
(1)求证:平面 平面 ;
(2)求三棱锥 的体积.
(3)
考点05 异面直线所成角及最值或范围
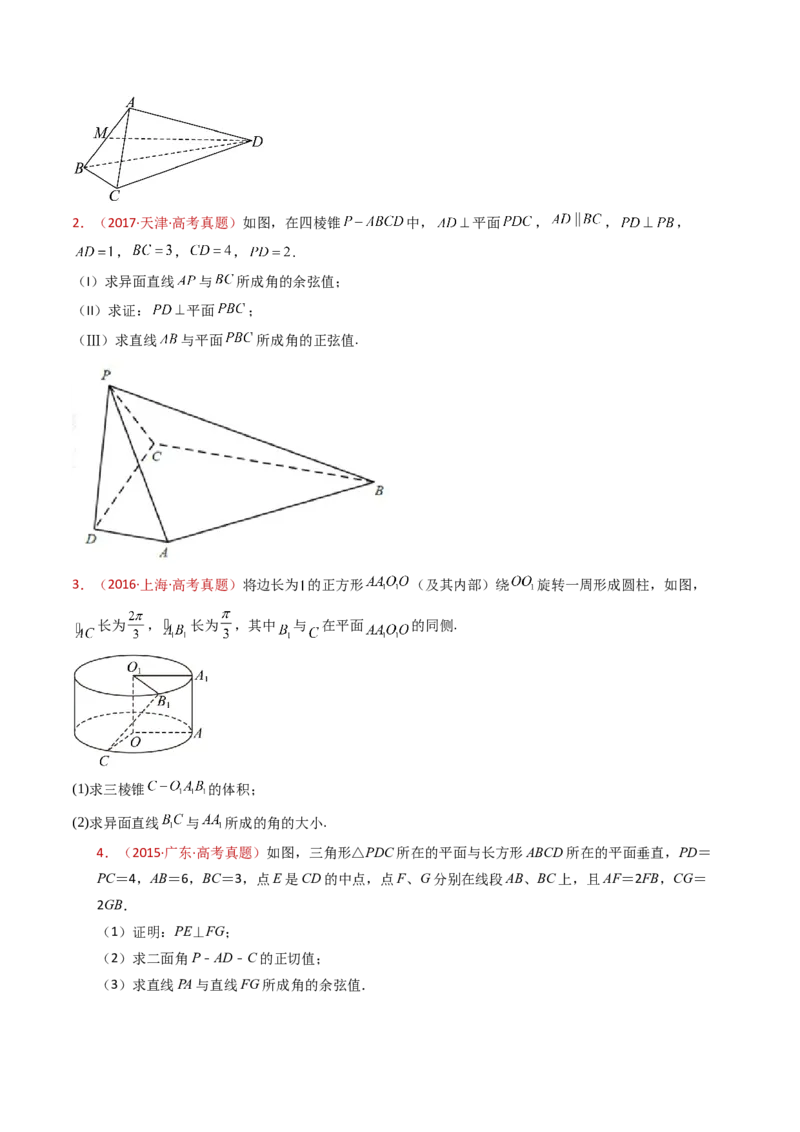
1.(2018·天津·高考真题)如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M
为棱AB的中点,AB=2,AD= ,∠BAD=90°.
(Ⅰ)求证:AD⊥BC;
(Ⅱ)求异面直线BC与MD所成角的余弦值;
(Ⅲ)求直线CD与平面ABD所成角的正弦值.2.(2017·天津·高考真题)如图,在四棱锥 中, 平面 , , ,
, , , .
(I)求异面直线 与 所成角的余弦值;
(II)求证: 平面 ;
(Ⅲ)求直线 与平面 所成角的正弦值.
3.(2016·上海·高考真题)将边长为 的正方形 (及其内部)绕 旋转一周形成圆柱,如图,
长为 , 长为 ,其中 与 在平面 的同侧.
(1)求三棱锥 的体积;
(2)求异面直线 与 所成的角的大小.
4.(2015·广东·高考真题)如图,三角形△PDC所在的平面与长方形ABCD所在的平面垂直,PD=
PC=4,AB=6,BC=3,点E是CD的中点,点F、G分别在线段AB、BC上,且AF=2FB,CG=
2GB.
(1)证明:PE⊥FG;
(2)求二面角P﹣AD﹣C的正切值;
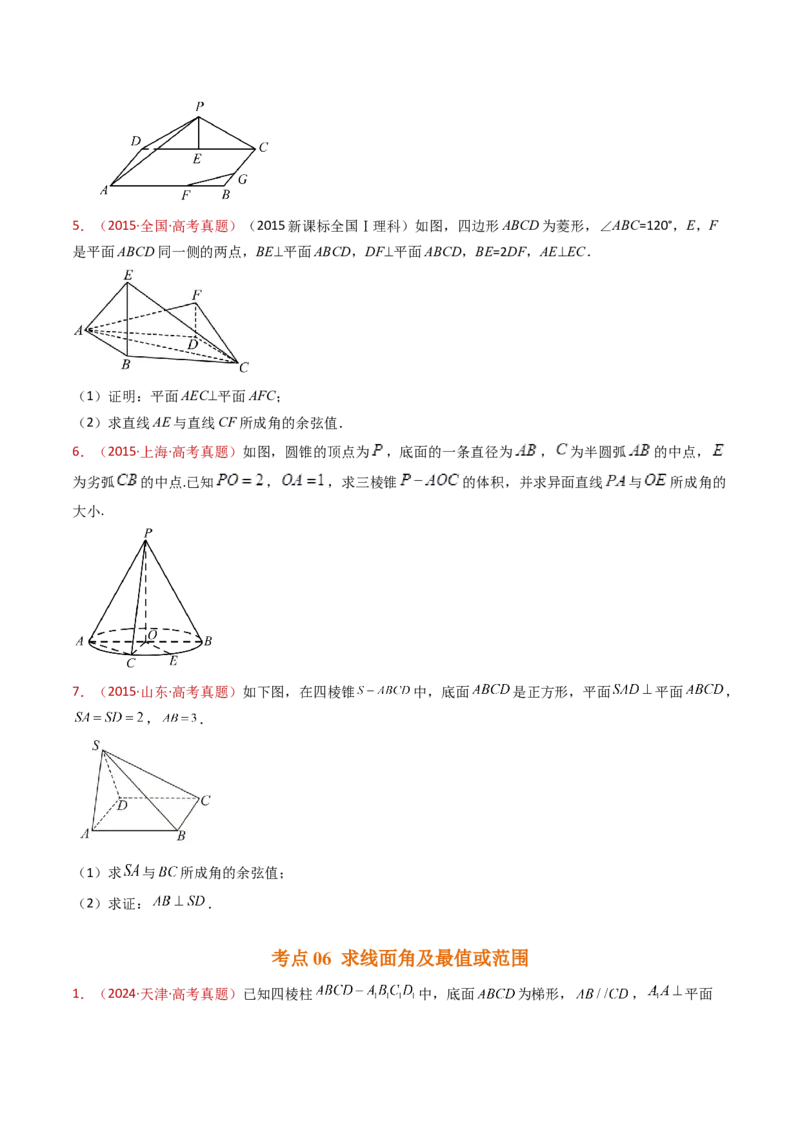
(3)求直线PA与直线FG所成角的余弦值.5.(2015·全国·高考真题)(2015新课标全国Ⅰ理科)如图,四边形ABCD为菱形,∠ABC=120°,E,F
是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.
(1)证明:平面AEC⊥平面AFC;
(2)求直线AE与直线CF所成角的余弦值.
6.(2015·上海·高考真题)如图,圆锥的顶点为 ,底面的一条直径为 , 为半圆弧 的中点,
为劣弧 的中点.已知 , ,求三棱锥 的体积,并求异面直线 与 所成角的
大小.
7.(2015·山东·高考真题)如下图,在四棱锥 中,底面 是正方形,平面 平面 ,
, .
(1)求 与 所成角的余弦值;
(2)求证: .
考点06 求线面角及最值或范围
1.(2024·天津·高考真题)已知四棱柱 中,底面 为梯形, , 平面, ,其中 . 是 的中点, 是 的中点.
(1)求证 平面 ;
(2)求平面 与平面 的夹角余弦值;
(3)求点 到平面 的距离.
2.(2024·上海·高考真题)如图为正四棱锥 为底面 的中心.
(1)若 ,求 绕 旋转一周形成的几何体的体积;
(2)若 为 的中点,求直线 与平面 所成角的大小.
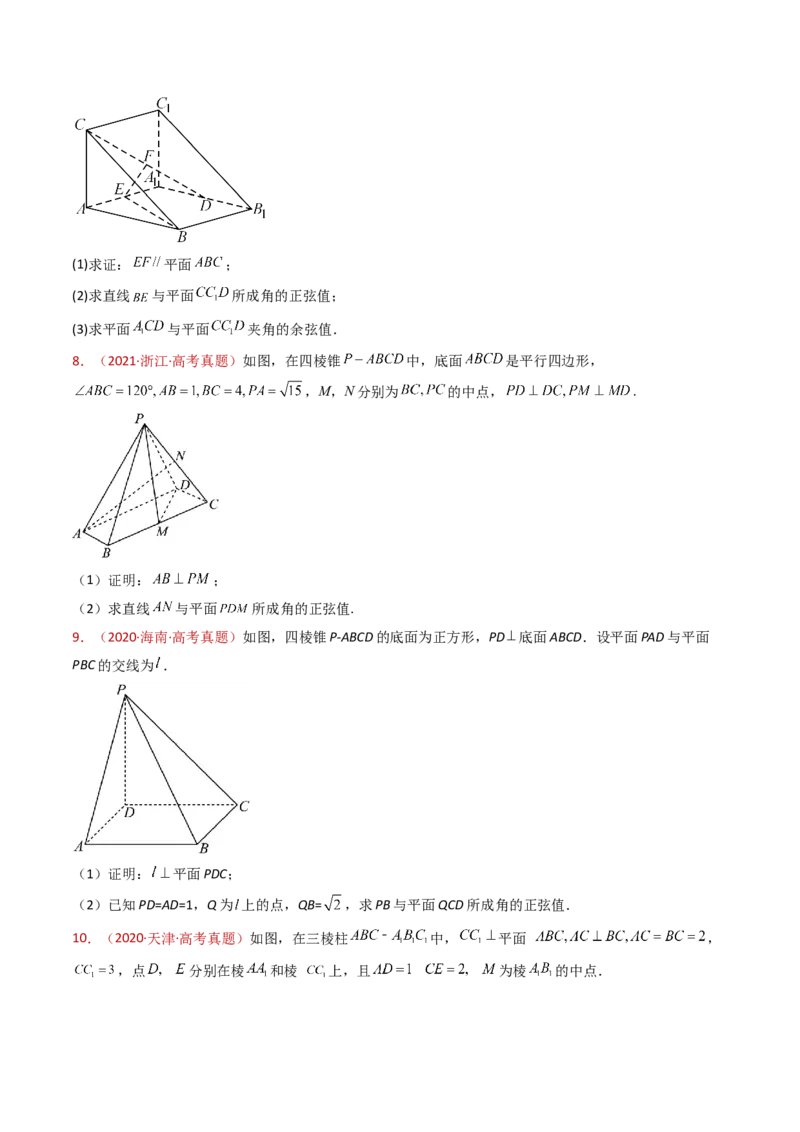
3.(2023·全国甲卷·高考真题)如图,在三棱柱 中, 底面ABC,
, 到平面 的距离为1.
(1)证明: ;
(2)已知 与 的距离为2,求 与平面 所成角的正弦值.
4.(2022·全国甲卷·高考真题)在四棱锥 中, 底面
.(1)证明: ;
(2)求PD与平面 所成的角的正弦值.
5.(2022·全国乙卷·高考真题)如图,四面体 中, ,E为 的
中点.
(1)证明:平面 平面 ;
(2)设 ,点F在 上,当 的面积最小时,求 与平面 所成的角的正
弦值.
6.(2022·浙江·高考真题)如图,已知 和 都是直角梯形, , , ,
, , ,二面角 的平面角为 .设M,N分别为 的
中点.
(1)证明: ;
(2)求直线 与平面 所成角的正弦值.
7.(2022·天津·高考真题)直三棱柱 中, ,D为
的中点,E为 的中点,F为 的中点.(1)求证: 平面 ;
(2)求直线 与平面 所成角的正弦值;
(3)求平面 与平面 夹角的余弦值.
8.(2021·浙江·高考真题)如图,在四棱锥 中,底面 是平行四边形,
,M,N分别为 的中点, .
(1)证明: ;
(2)求直线 与平面 所成角的正弦值.
9.(2020·海南·高考真题)如图,四棱锥P-ABCD的底面为正方形,PD 底面ABCD.设平面PAD与平面
PBC的交线为 .
(1)证明: 平面PDC;
(2)已知PD=AD=1,Q为 上的点,QB= ,求PB与平面QCD所成角的正弦值.
10.(2020·天津·高考真题)如图,在三棱柱 中, 平面 ,
,点 分别在棱 和棱 上,且 为棱 的中点.(Ⅰ)求证: ;
(Ⅱ)求二面角 的正弦值;
(Ⅲ)求直线 与平面 所成角的正弦值.
11.(2020·北京·高考真题)如图,在正方体 中, E为 的中点.
(Ⅰ)求证: 平面 ;
(Ⅱ)求直线 与平面 所成角的正弦值.
12.(2020·浙江·高考真题)如图,三棱台ABC—DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC
=2BC.
(I)证明:EF⊥DB;(II)求DF与面DBC所成角的正弦值.
13.(2020·山东·高考真题)如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平
面PBC的交线为l.
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
14.(2020·全国·高考真题)如图,已知三棱柱ABC-A B C 的底面是正三角形,侧面BB C C是矩形,M,N
1 1 1 1 1
分别为BC,B C 的中点,P为AM上一点,过B C 和P的平面交AB于E,交AC于F.
1 1 1 1
(1)证明:AA ∥MN,且平面A AMN⊥EB C F;
1 1 1 1
(2)设O为△A B C 的中心,若AO∥平面EB C F,且AO=AB,求直线B E与平面A AMN所成角的正弦值.
1 1 1 1 1 1 1
15.(2019·天津·高考真题) 如图,在四棱锥 中,底面 为平行四边形, 为等边三
角形,平面 平面 , , , ,(Ⅰ)设 分别为 的中点,求证: 平面 ;
(Ⅱ)求证: 平面 ;
(Ⅲ)求直线 与平面 所成角的正弦值.
16.(2019·浙江·高考真题)如图,已知三棱柱 ,平面 平面 , ,
分别是 的中点.
(1)证明: ;
(2)求直线 与平面 所成角的余弦值.
17.(2018·江苏·高考真题)如图,在正三棱柱ABC-ABC 中,AB=AA=2,点P,Q分别为AB,BC的中
1 1 1 1 1 1
点。
(1)求异面直线BP与AC 所成角的余弦值;
1
(2)求直线CC 与平面AQC 所成角的正弦值
1 1
18.(2018·浙江·高考真题)如图,已知多面体 均垂直于平面
.(Ⅰ)求证: 平面 ;
(Ⅱ)求直线 与平面 所成角的正弦值.
19.(2018·全国·高考真题)如图,四边形 为正方形, 分别为 的中点,以 为折痕把
折起,使点 到达点 的位置,且 .
(1)证明:平面 平面 ;
(2)求 与平面 所成角的正弦值.
20.(2018·天津·高考真题)如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点
M为棱AB的中点,AB=2,AD= ,∠BAD=90°.
(Ⅰ)求证:AD⊥BC;
(Ⅱ)求异面直线BC与MD所成角的余弦值;
(Ⅲ)求直线CD与平面ABD所成角的正弦值.
21.(2017·上海·高考真题)如图,直三棱柱 的底面为直角三角形,两直角边AB和AC的长
分别为4和2,侧棱 的长为5.
(1)求三棱柱 的体积;
(2)设M是BC中点,求直线 与平面 所成角的大小.22.(2017·天津·高考真题)如图,在四棱锥 中, 平面 , , ,
, , , .
(I)求异面直线 与 所成角的余弦值;
(II)求证: 平面 ;
(Ⅲ)求直线 与平面 所成角的正弦值.
23.(2017·浙江·高考真题)如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,
BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(I)证明:CE∥平面PAB;
(II)求直线CE与平面PBC所成角的正弦值
24.(2017·北京·高考真题)如图,在四棱锥 中,底面 为正方形,平面 平面 ,点 在线段 上, 平面 , , .
(1)求证: 为 的中点;
(2)求二面角 的大小;
(3)求直线 与平面 所成角的正弦值.
25.(2016·浙江·高考真题)如图,在三棱台ABC–DEF中,平面BCFE⊥平面ABC,∠ACB=90°,
BE=EF=FC=1,BC=2,AC=3.
(Ⅰ)求证:BF⊥平面ACFD;
(Ⅱ)求直线BD与平面ACFD所成角的余弦值.
26.(2016·天津·高考真题)如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面
ABCD,点G为AB的中点,AB=BE=2.
(Ⅰ)求证:EG∥平面ADF;
(Ⅱ)求二面角O−EF−C的正弦值;
(Ⅲ)设H为线段AF上的点,且AH= HF,求直线BH和平面CEF所成角的正弦值.
27.(2016·全国·高考真题)如图,四棱锥P−ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,
PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
28.(2016·北京·高考真题)如图,在四棱锥 中,平面 平面 , , ,
, , , .
(1)求证: 平面 ;
(2)求直线 与平面 所成角的正弦值;
(3)在棱 上是否存在点 ,使得 平面 ?若存在,求 的值;若不存在,说明理由.
29.(2016·天津·高考真题)如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF||AB,AB=2,
BC=EF=1,AE= ,DE=3,∠BAD=60º,G为BC的中点.
(Ⅰ)求证:FG||平面BED;
(Ⅱ)求证:平面BED⊥平面AED;
(Ⅲ)求直线EF与平面BED所成角的正弦值.
30.(2015·广东·高考真题)如图,三角形△PDC所在的平面与长方形ABCD所在的平面垂直,PD=
PC=4,AB=6,BC=3,点E是CD的中点,点F、G分别在线段AB、BC上,且AF=2FB,CG=2GB.
(1)证明:PE⊥FG;
(2)求二面角P﹣AD﹣C的正切值;
(3)求直线PA与直线FG所成角的余弦值.
31.(2015·浙江·高考真题)如图,在三棱锥 中, 在底
面ABC的射影为BC的中点,D为 的中点.
(1)证明: ;
(2)求直线 和平面 所成的角的正弦值.
32.(2015·天津·高考真题)如图,已知 平面ABC, AB=AC=3, ,,
点E,F分别是BC, 的中点.
(Ⅰ)求证:EF∥平面 ;
(Ⅱ)求证:平面 平面 .
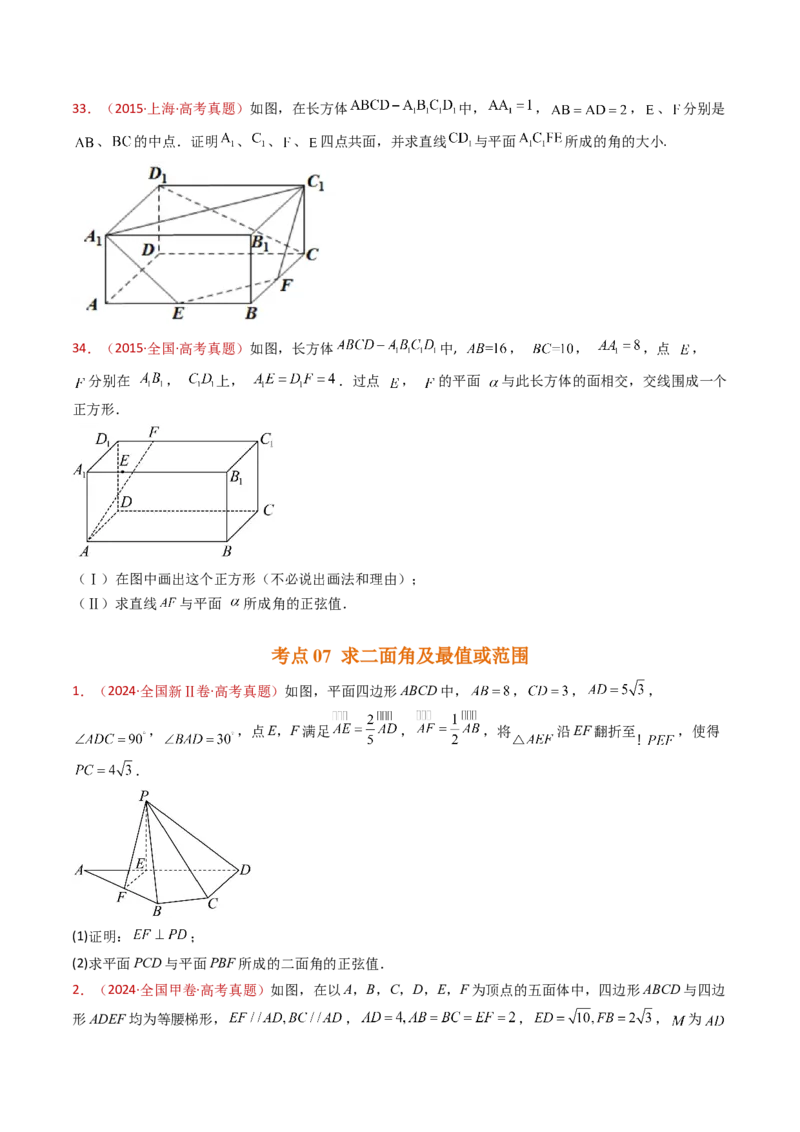
(Ⅲ)求直线 与平面 所成角的大小.33.(2015·上海·高考真题)如图,在长方体 中, , , 、 分别是
、 的中点.证明 、 、 、 四点共面,并求直线 与平面 所成的角的大小.
34.(2015·全国·高考真题)如图,长方体 中, , , ,点 ,
分别在 , 上, .过点 , 的平面 与此长方体的面相交,交线围成一个
正方形.
(Ⅰ)在图中画出这个正方形(不必说出画法和理由);
(Ⅱ)求直线 与平面 所成角的正弦值.
考点07 求二面角及最值或范围
1.(2024·全国新Ⅱ卷·高考真题)如图,平面四边形ABCD中, , , ,
, ,点E,F满足 , ,将 沿EF翻折至 ,使得
.
(1)证明: ;
(2)求平面PCD与平面PBF所成的二面角的正弦值.
2.(2024·全国甲卷·高考真题)如图,在以A,B,C,D,E,F为顶点的五面体中,四边形ABCD与四边
形ADEF均为等腰梯形, , , , 为的中点.
(1)证明: 平面 ;
(2)求二面角 的正弦值.
3.(2024·北京·高考真题)如图,在四棱锥 中, , , ,点 在 上,
且 , .
(1)若 为线段 中点,求证: 平面 .
(2)若 平面 ,求平面 与平面 夹角的余弦值.
4.(2024·天津·高考真题)已知四棱柱 中,底面 为梯形, , 平面
, ,其中 . 是 的中点, 是 的中点.
(1)求证 平面 ;
(2)求平面 与平面 的夹角余弦值;
(3)求点 到平面 的距离.
5.(2023·全国新Ⅱ卷·高考真题)如图,三棱锥 中, , ,
,E为BC的中点.(1)证明: ;
(2)点F满足 ,求二面角 的正弦值.
6.(2023·全国乙卷·高考真题)如图,在三棱锥 中, , , ,
,BP,AP,BC的中点分别为D,E,O, ,点F在AC上, .
(1)证明: 平面 ;
(2)证明:平面 平面BEF;
(3)求二面角 的正弦值.
7.(2023·北京·高考真题)如图,在三棱锥 中, 平面 , .
(1)求证: 平面PAB;
(2)求二面角 的大小.
8.(2023·天津·高考真题)如图,在三棱台 中, 平面
, 为 中点.,N为AB的中点,(1)求证: //平面 ;
(2)求平面 与平面 所成夹角的余弦值;
(3)求点 到平面 的距离.
9.(2022·全国新Ⅰ卷·高考真题)如图,直三棱柱 的体积为4, 的面积为 .
(1)求A到平面 的距离;
(2)设D为 的中点, ,平面 平面 ,求二面角 的正弦值.
10.(2022·全国新Ⅱ卷·高考真题)如图, 是三棱锥 的高, , ,E是 的中
点.
(1)证明: 平面 ;
(2)若 , , ,求二面角 的正弦值.
11.(2022·天津·高考真题)直三棱柱 中, ,D为的中点,E为 的中点,F为 的中点.
(1)求证: 平面 ;
(2)求直线 与平面 所成角的正弦值;
(3)求平面 与平面 夹角的余弦值.
12.(2021·全国新Ⅱ卷·高考真题)在四棱锥 中,底面 是正方形,若
.
(1)证明:平面 平面 ;
(2)求二面角 的平面角的余弦值.
13.(2021·全国甲卷·高考真题)已知直三棱柱 中,侧面 为正方形, ,
E,F分别为 和 的中点,D为棱 上的点.
(1)证明: ;
(2)当 为何值时,面 与面 所成的二面角的正弦值最小?
14.(2021·全国乙卷·高考真题)如图,四棱锥 的底面是矩形, 底面 , ,
为 的中点,且 .(1)求 ;
(2)求二面角 的正弦值.
15.(2021·天津·高考真题)如图,在棱长为2的正方体 中,E为棱BC的中点,F为棱
CD的中点.
(I)求证: 平面 ;
(II)求直线 与平面 所成角的正弦值.
(III)求二面角 的正弦值.
16.(2020·天津·高考真题)如图,在三棱柱 中, 平面 ,
,点 分别在棱 和棱 上,且 为棱 的中点.(Ⅰ)求证: ;
(Ⅱ)求二面角 的正弦值;
(Ⅲ)求直线 与平面 所成角的正弦值.
17.(2020·江苏·高考真题)在三棱锥A—BCD中,已知CB=CD= ,BD=2,O为BD的中点,AO⊥平面
BCD,AO=2,E为AC的中点.
(1)求直线AB与DE所成角的余弦值;
(2)若点F在BC上,满足BF= BC,设二面角F—DE—C的大小为θ,求sinθ的值.
18.(2020·全国·高考真题)如图,在长方体 中,点 分别在棱 上,且
, .
(1)证明:点 在平面 内;
(2)若 , , ,求二面角 的正弦值.
19.(2020·全国·高考真题)如图, 为圆锥的顶点, 是圆锥底面的圆心, 为底面直径, .
是底面的内接正三角形, 为 上一点, .(1)证明: 平面 ;
(2)求二面角 的余弦值.
20.(2019·北京·高考真题)如图,在四棱锥P–ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,
PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且 .
(Ⅰ)求证:CD⊥平面PAD;
(Ⅱ)求二面角F–AE–P的余弦值;
(Ⅲ)设点G在PB上,且 .判断直线AG是否在平面AEF内,说明理由.
21.(2019·全国·高考真题)图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中
AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B−CG−A的大小.22.(2019·全国·高考真题)如图,长方体ABCD–ABC D 的底面ABCD是正方形,点E在棱AA 上,
1 1 1 1 1
BE⊥EC .
1
(1)证明:BE⊥平面EBC ;
1 1
(2)若AE=AE,求二面角B–EC–C 的正弦值.
1 1
23.(2019·全国·高考真题)如图,直四棱柱ABCD–ABC D 的底面是菱形,AA=4,AB=2,∠BAD=60°,
1 1 1 1 1
E,M,N分别是BC,BB,AD的中点.
1 1
(1)证明:MN∥平面C DE;
1
(2)求二面角A-MA-N的正弦值.
1
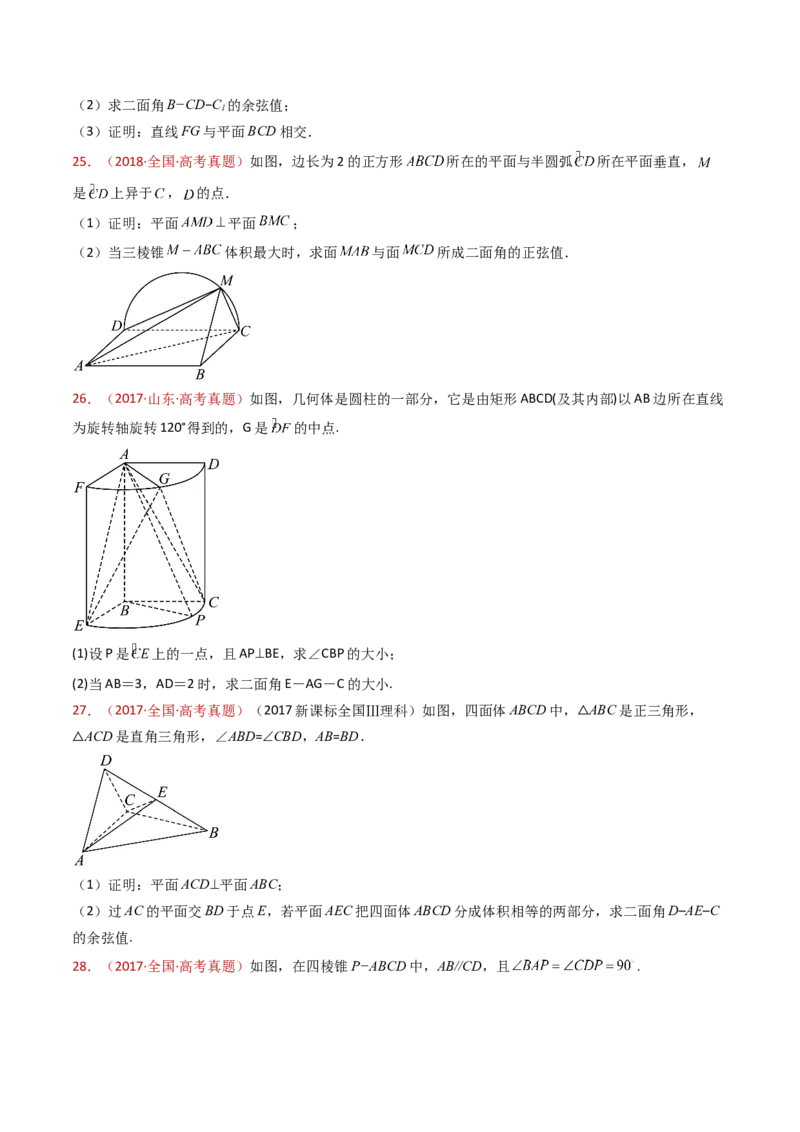
24.(2018·北京·高考真题)如图,在三棱柱ABC− 中, 平面ABC,D,E,F,G分别为 ,
AC, , 的中点,AB=BC= ,AC= =2.
(1)求证:AC⊥平面BEF;(2)求二面角B−CD−C 的余弦值;
1
(3)证明:直线FG与平面BCD相交.
25.(2018·全国·高考真题)如图,边长为2的正方形 所在的平面与半圆弧 所在平面垂直,
是 上异于 , 的点.
(1)证明:平面 平面 ;
(2)当三棱锥 体积最大时,求面 与面 所成二面角的正弦值.
26.(2017·山东·高考真题)如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线
为旋转轴旋转120°得到的,G是 的中点.
(1)设P是 上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
27.(2017·全国·高考真题)(2017新课标全国Ⅲ理科)如图,四面体ABCD中, ABC是正三角形,
ACD是直角三角形,∠ABD=∠CBD,AB=BD.
△
△
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C
的余弦值.
28.(2017·全国·高考真题)如图,在四棱锥P−ABCD中,AB//CD,且 .(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ,求二面角A−PB−C的余弦值.
29.(2017·江苏·高考真题)如图,在平行六面体ABCD-A B C D 中,AA ⊥平面ABCD,且AB=AD=2,
1 1 1 1 1
AA = ,∠BAD=120°.
1
(1)求异面直线A B与AC 所成角的余弦值;
1 1
(2)求二面角B-A D-A的正弦值.
1
30.(2016·天津·高考真题)如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面
ABCD,点G为AB的中点,AB=BE=2.
(Ⅰ)求证:EG∥平面ADF;
(Ⅱ)求二面角O−EF−C的正弦值;
(Ⅲ)设H为线段AF上的点,且AH= HF,求直线BH和平面CEF所成角的正弦值.
31.(2016·山东·高考真题)在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O 的直径,FB
是圆台的一条母线.(Ⅰ)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(Ⅱ)已知EF=FB= AC= ,AB=BC.求二面角 的余弦值.
32.(2016·浙江·高考真题)如图,在三棱台 中,平面 平面 ,
.
(Ⅰ)求证: 平面 ;
(Ⅱ)求二面角 的平面角的余弦值.
33.(2016·全国·高考真题)如图,菱形 的对角线 与 交于点 ,点 分别在
上, 交 于点 ,将 沿 折到 位置, .
(1)证明: 平面 ;
(2)求二面角 的正弦值.
34.(2016·全国·高考真题)如图,在以 , , , , , 为顶点的五面体中,四边形 为正方
形, , ,且二面角 与二面角 都是 .
(1)证明:平面 平面 ;
(2)求二面角 的余弦值.
35.(2015·广东·高考真题)如图,三角形△PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=
4,AB=6,BC=3,点E是CD的中点,点F、G分别在线段AB、BC上,且AF=2FB,CG=2GB.(1)证明:PE⊥FG;
(2)求二面角P﹣AD﹣C的正切值;
(3)求直线PA与直线FG所成角的余弦值.
36.(2015·重庆·高考真题)如图,三棱锥 中, 平面
, , . 分别为线段 上的点,且 .
(1)证明: 平面 ;
(2)求二面角 的余弦值.
37.(2015·浙江·高考真题)如图,在三棱柱 -中, , , ,
在底面 的射影为 的中点, 为 的中点.
(1)证明: D 平面 ;
(2)求二面角 -BD- 的平面角的余弦值.
38.(2015·四川·高考真题)一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设 的中点为 , 的中点为
(1)请将字母 标记在正方体相应的顶点处(不需说明理由)
(2)证明:直线 平面
(3)求二面角 的余弦值.
39.(2015·陕西·高考真题)如图 ,在直角梯形 中, , , ,
, 是 的中点, 是 与 的交点.将 沿 折起到 的位置,如图 .
(Ⅰ)证明: 平面 ;
(Ⅱ)若平面 平面 ,求平面 与平面 夹角的余弦值.
40.(2015·山东·高考真题)如图,在三棱台 中, 分别为 的中点.
(Ⅰ)求证: 平面 ;
(Ⅱ)若 平面 , ,
,求平面 与平面 所成角(锐角)的大小.
41.(2015·安徽·高考真题)如图所示,在多面体 ,四边形 , 均为正方
形, 为 的中点,过 的平面交 于F.(Ⅰ)证明: ;
(Ⅱ)求二面角 余弦值.
42.(2015·福建·高考真题)如图,在几何体 中,四边形 是矩形, 平面 ,
, , , 分别是线段 , 的中点.
(1)求证: 平面 ;
(2)求平面 与平面 所成锐二面角的余弦值.
43.(2015·北京·高考真题)如图,在四棱锥 中, 为等边三角形,平面 平面 ,
, , , , 为 的中点.
( )求证: .
( )求二面角 的余弦值.
( )若 平面 ,求 的值.
考点08 已知异面直线所成角、线面角、二面角求值或范围(方程思想)
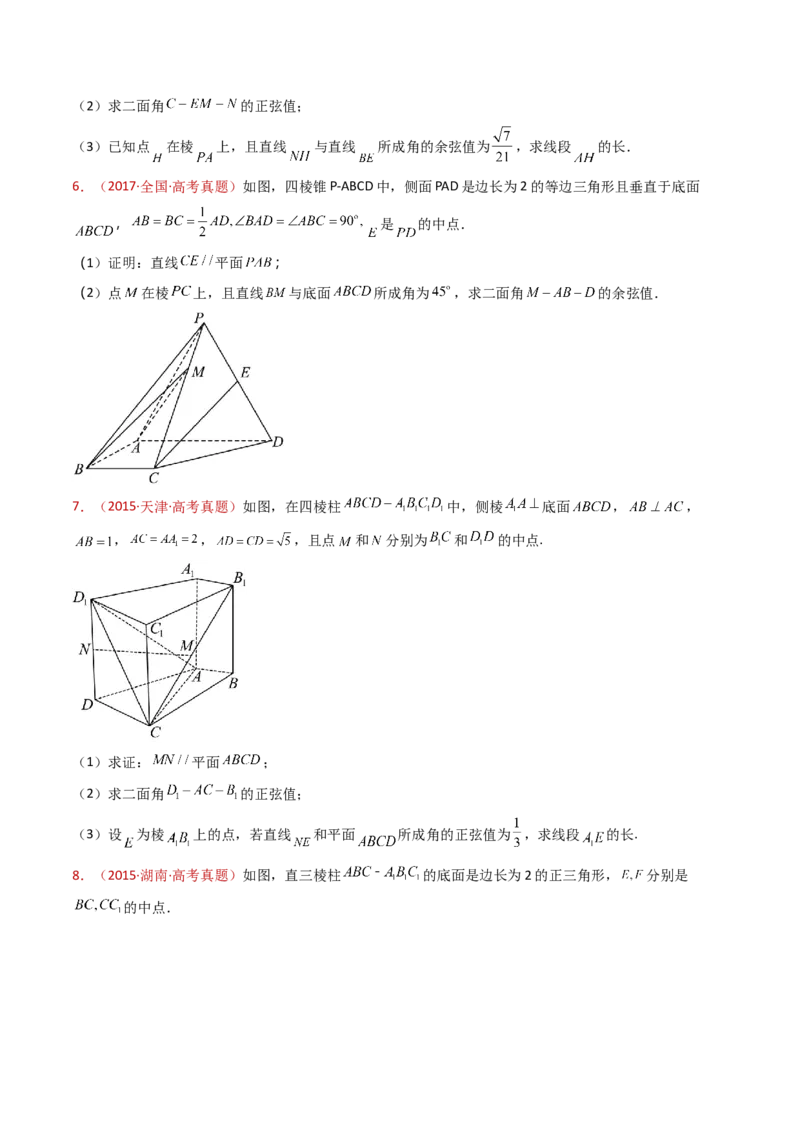
1.(2024·全国新Ⅰ卷·高考真题)如图,四棱锥 中, 底面ABCD, ,
.(1)若 ,证明: 平面 ;
(2)若 ,且二面角 的正弦值为 ,求 .
2.(2023·全国新Ⅰ卷·高考真题)如图,在正四棱柱 中, .点
分别在棱 , 上, .
(1)证明: ;
(2)点 在棱 上,当二面角 为 时,求 .
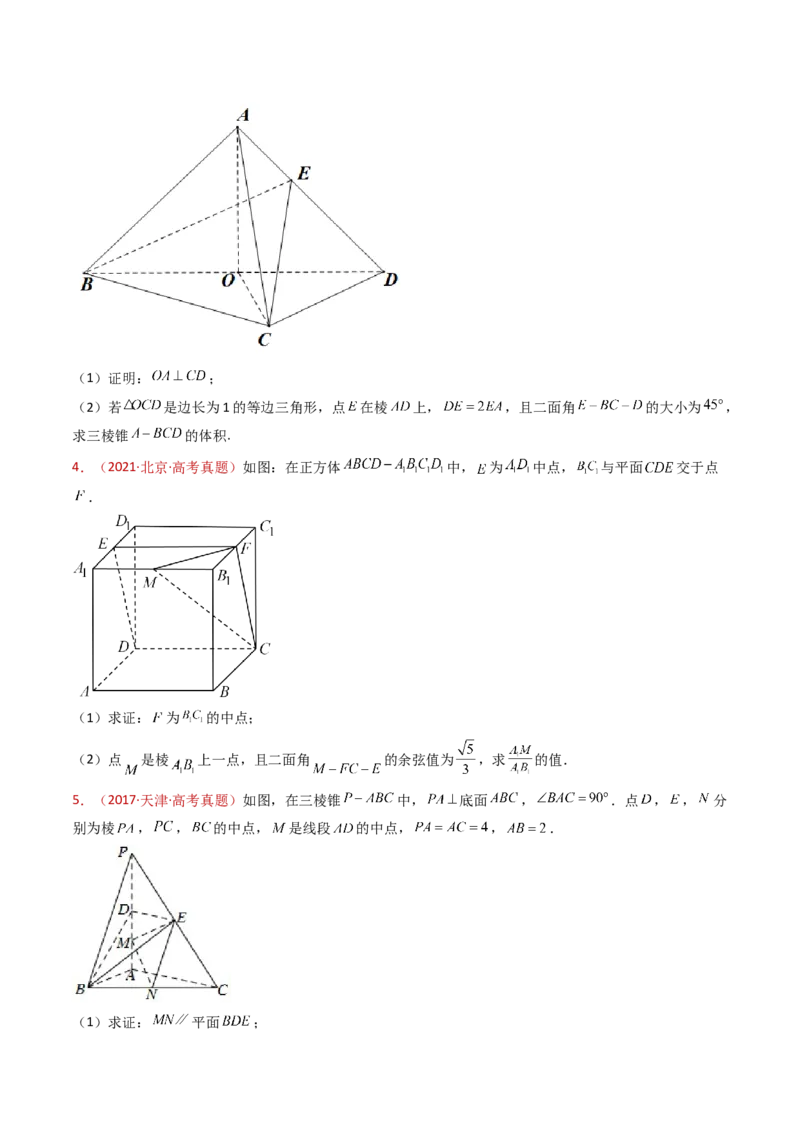
3.(2021·全国新Ⅰ卷·高考真题)如图,在三棱锥 中,平面 平面 , , 为
的中点.(1)证明: ;
(2)若 是边长为1的等边三角形,点 在棱 上, ,且二面角 的大小为 ,
求三棱锥 的体积.
4.(2021·北京·高考真题)如图:在正方体 中, 为 中点, 与平面 交于点
.
(1)求证: 为 的中点;
(2)点 是棱 上一点,且二面角 的余弦值为 ,求 的值.
5.(2017·天津·高考真题)如图,在三棱锥 中, 底面 , .点 , , 分
别为棱 , , 的中点, 是线段 的中点, , .
(1)求证: 平面 ;(2)求二面角 的正弦值;
(3)已知点 在棱 上,且直线 与直线 所成角的余弦值为 ,求线段 的长.
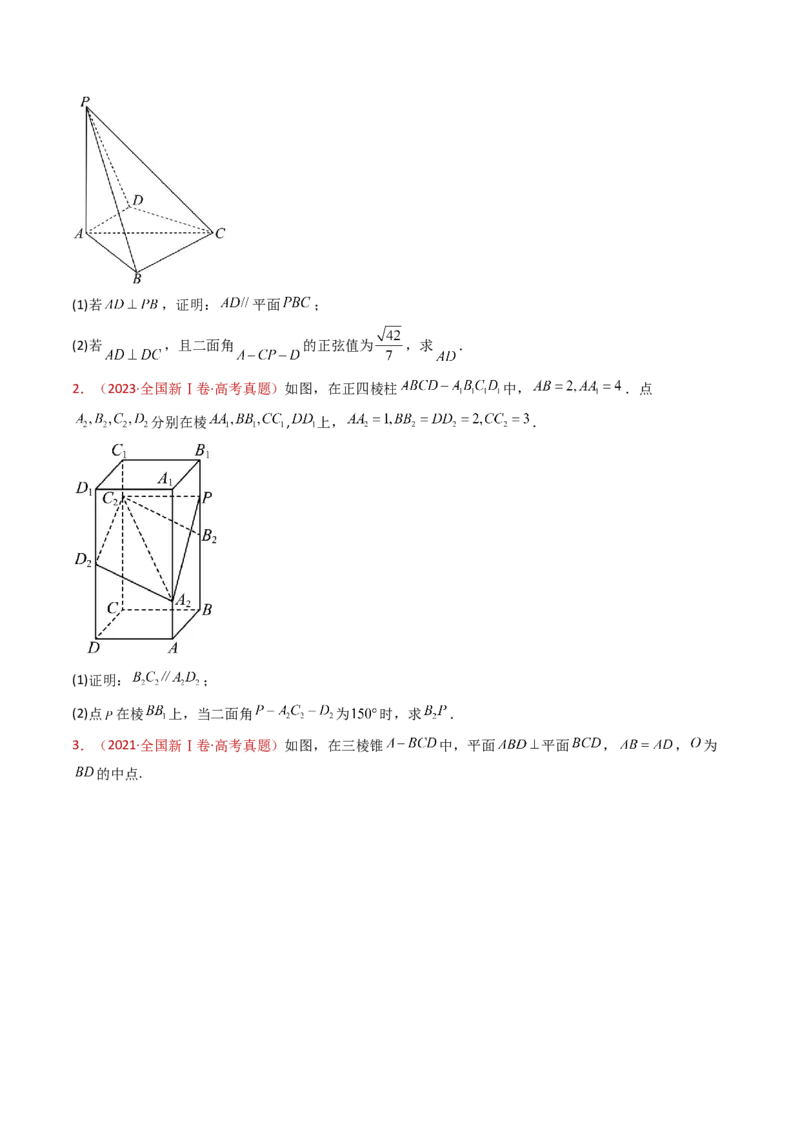
6.(2017·全国·高考真题)如图,四棱锥P-ABCD中,侧面PAD是边长为2的等边三角形且垂直于底面
, 是 的中点.
(1)证明:直线 平面 ;
(2)点 在棱 上,且直线 与底面 所成角为 ,求二面角 的余弦值.
7.(2015·天津·高考真题)如图,在四棱柱 中,侧棱 底面 , ,
, , ,且点 和 分别为 和 的中点.
(1)求证: 平面 ;
(2)求二面角 的正弦值;
(3)设 为棱 上的点,若直线 和平面 所成角的正弦值为 ,求线段 的长.
8.(2015·湖南·高考真题)如图,直三棱柱 的底面是边长为2的正三角形, 分别是
的中点.(1)证明:平面 平面 ;
(2)若直线 与平面 所成的角为 ,求三棱锥 的体积.
9.(2015·湖南·高考真题)如图,已知四棱台 的上、下底面分别是边长为3和6的正方形,
,且 底面 ,点 分别在棱 上.
(1)若 是 的中点,证明: ;
(2)若 平面 ,二面角 的余弦值为 ,求四面体 的体积.
10.(2015·湖北·高考真题)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为
阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马 中,侧棱 底面 ,且 ,过棱 的中点 ,作 交
于点 ,连接
(Ⅰ)证明: .试判断四面体 是否为鳖臑,若是,写出其每个面的直角(只需写
出结论);若不是,说明理由;
(Ⅱ)若面 与面 所成二面角的大小为 ,求 的值.