文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷
(新高考Ⅱ卷专用)
黄金卷01
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。
1.设集合 , ,且 ,则 ( )
A.6 B.4 C. D.
2.已知 ,则 ( ).
A. B. C.2 D.1
3.已知 的图象与直线 在区间 上存在两个交点,则当 最大时,曲线
的对称轴为( )
A. , B. ,
C. , D. ,
4.函数 的图像大致为( )
A. B.C. D.
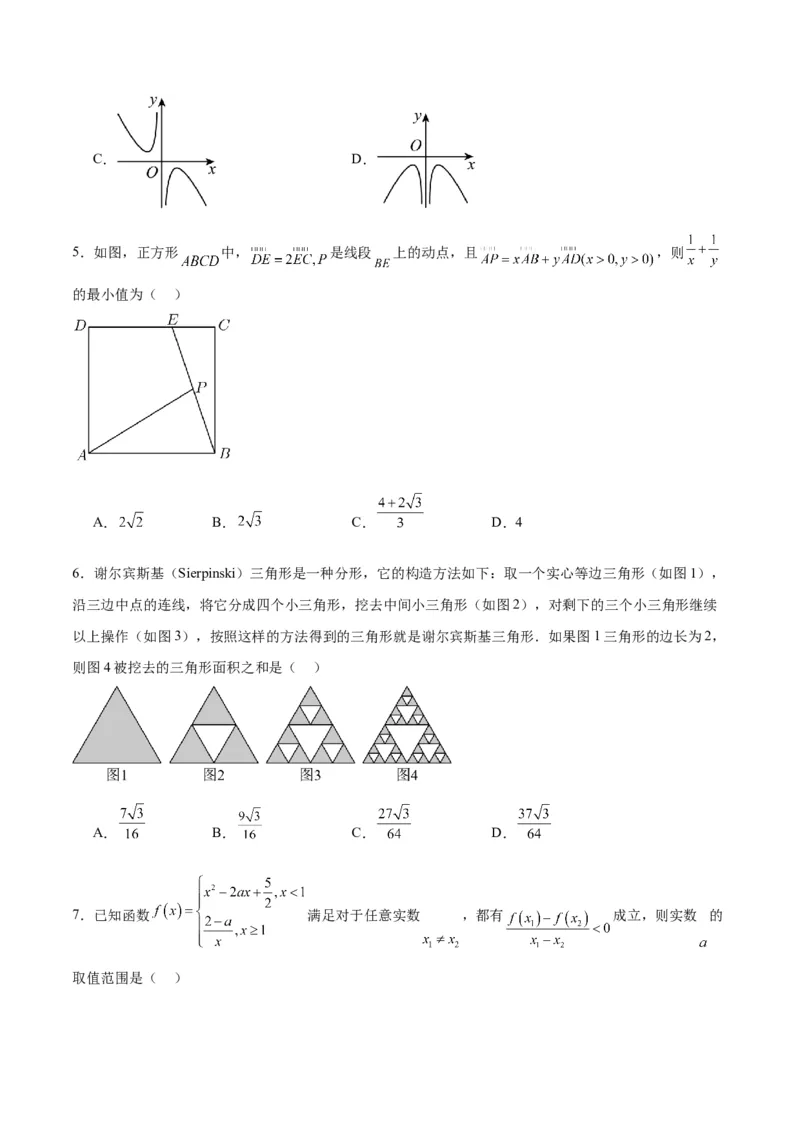
5.如图,正方形 中, 是线段 上的动点,且 ,则
的最小值为( )
A. B. C. D.4
6.谢尔宾斯基(Sierpinski)三角形是一种分形,它的构造方法如下:取一个实心等边三角形(如图1),
沿三边中点的连线,将它分成四个小三角形,挖去中间小三角形(如图2),对剩下的三个小三角形继续
以上操作(如图3),按照这样的方法得到的三角形就是谢尔宾斯基三角形.如果图1三角形的边长为2,
则图4被挖去的三角形面积之和是( )
A. B. C. D.
7.已知函数 满足对于任意实数 ,都有 成立,则实数 的
取值范围是( )A. B. C. D.
8.已知双曲线 右支上非顶点的一点A关于原点的对称点为 为双曲线的右焦点,若
,设 ,且 ,则该双曲线的离心率的取值范围为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的
要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知圆M: ,则下列关于圆M的结论正确的是( )
A.点 在圆M内
B.圆M关于直线 对称
C.圆M与圆O: 相切
D.若直线l过点 ,且被圆M截得的弦长为 ,则l的方程为
10.下列说法正确的是( )
A.若数据 的方差为1,则新数据 , ,…, 的方差为1
B.已知随机事件A和B互斥,且 , ,则 等于0.5.
C.“ ”是直线 与直线 互相垂直的充要条件
D.无论实数λ取何值,直线 恒过定点
11.如图,在棱长为2的正方体 中, , 分别是棱 , 的中点,点 在 上,
点 在 上,且 ,点 在线段 上运动,下列说法正确的有( )A.当点 是 中点时,直线 平面 ;
B.直线 到平面 的距离是 ;
C.存在点 ,使得 ;
D. 面积的最小值是
12.已知 、 都是定义在 上的函数,且 为奇函数, 的图像关于直线 对称,则下
列说法中一定正确的是( )
A. B.
C. 为奇函数 D. 的图像关于直线 对称
第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.已知 的展开式中各项系数的和为 ,则实数 的值为 .
14.已知等差数列 的前 项和分别为 ,且 ,则 .
15.在 中,角 , , 所对的边分别为 , , ,已知 , , ,则
的最大值为 .
16.在棱长为2的正方体 中,点M是对角线 上的点(点M与A、 不重合),则下列结论正确的是 .(请填写序号)
①存在点M,使得平面 平面 ;
②存在点M,使得 平面 ;
③若 的面积为S,则 ;
④若 、 分别是 在平面 与平面 的正投影的面积,则存在点M,使得 .
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.(10分)已知点 是角 终边上一点.
(1)求 的值;
(2)若将角 终边绕着坐标原点逆时针旋转 得到角 的终边,求 的值.
18.(12分)已知正项数列 的前 项和 ,满足: .
(1)求数列 的通项公式;
(2)记 ,设数列 的前 项和为 ,求证 .
19.(12分)如图,在四棱柱 中,四棱锥 是正四棱锥, .(1)求 与平面 所成角的正弦值;
(2)若四棱柱 的体积为16,点 在棱 上,且 ,求点 到平面 的距离.
20.(12分)第19届亚运会于9月23日至10月8日在杭州举行,某学校为持续营造全民参与亚运、服务
亚运、奉献亚运的浓厚氛围举办“心心相融·爱答亚运”知识挑战赛.挑战者向守擂者提出挑战,规则为挑
战者和守擂者轮流答题,直至一方答不出或答错,则另一方自动获胜.若赛制要求挑战者先答题,守擂者
和挑战者每次答对问题的概率都是 ,且每次答题互不影响.
(1)若在不多于两次答题就决出胜负,则挑战者获胜的概率是多少?
(2)在此次比赛中,挑战者获胜的概率是多少?
(3)现赛制改革,挑战者需要按上述方式连续挑战8位守擂者,每次挑战之间相互独立,当战胜至少三分之
二以上的守擂者时,则称该挑战者胜利.若再增加1位守擂者时,试分析该挑战者胜利的概率是否增加?并
说明理由.
21.(12分)已知椭圆 : ,点 、 分别是椭圆 的左焦点、左顶
点,过点 的直线 (不与x轴重合)交椭圆 于A,B两点.
(1)求椭圆M的标准方程;(2)若 ,求 的面积;
(3)是否存在直线 ,使得点B在以线段 为直径的圆上,若存在,求出直线 的方程;若不存在,请说明
理由.
22.(12分)已知函数 .
(1)求 的极值;
(2)若 在区间 有2个零点,求 的取值范围.