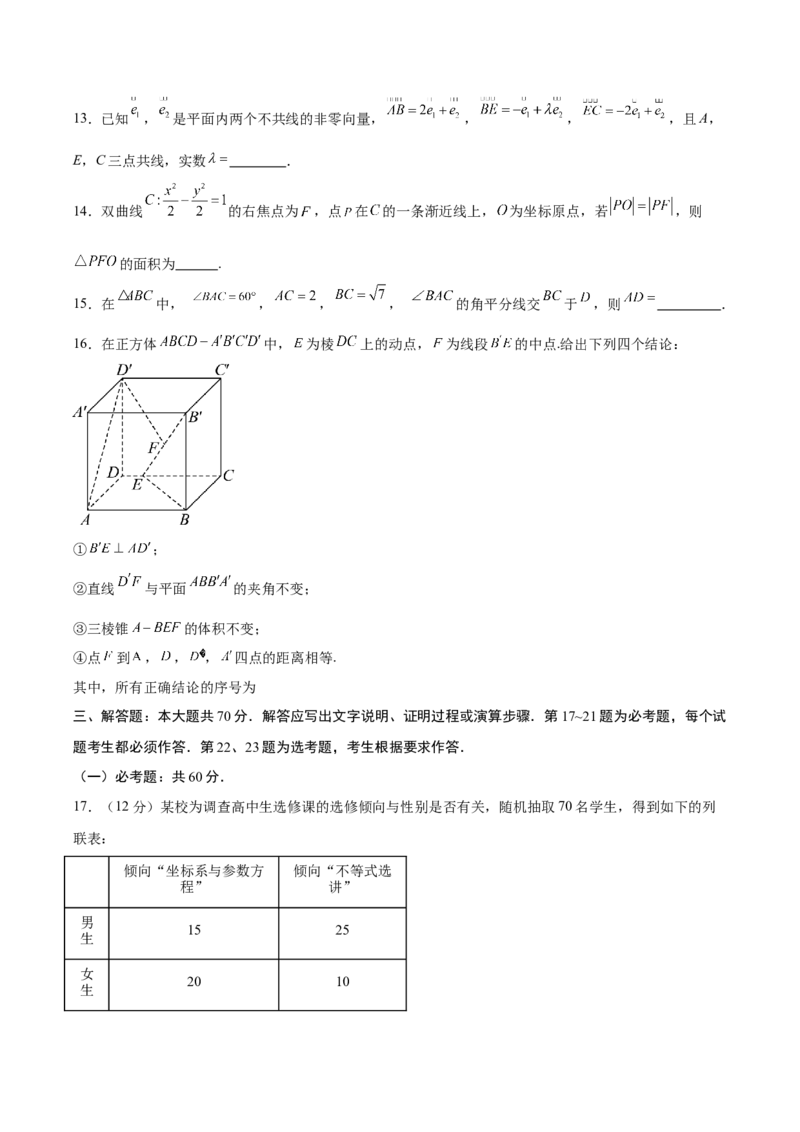文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(全国卷专用)
黄金卷01
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.已知集合 , ,则 ( )
A. B. C. D.
2.复数 在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列结论正确的有( )
① 是 的充要条件
② 的最小值为2
③命题“ , ”的否定是“ , ”
④关于x的不等式 有解,实数a的范围是 或 .
A.①②③④ B.①③④ C.②③④ D.③④
4.(河北省石家庄市2023届高三三模数学试题)已知函数 同时满足性质:① ;②对
于 , ,则函数 可能是( )
A. B.C. D.
5.在直三棱柱 中, ,M,N分别是 , 的中点, ,则AM
与CN所成角的余弦值为( )
A. B. C. D.
6.2023年3月5号是毛泽东主席提出“向雷锋同志学习”60周年纪念日,某志愿者服务队在该日安排4
位志愿者到两所敬老院开展志愿服务活动,要求每所敬老院至少安排1人,每个志愿者都要参加活动,则
不同的分配方法数是( )
A.8 B.12 C.14 D.20
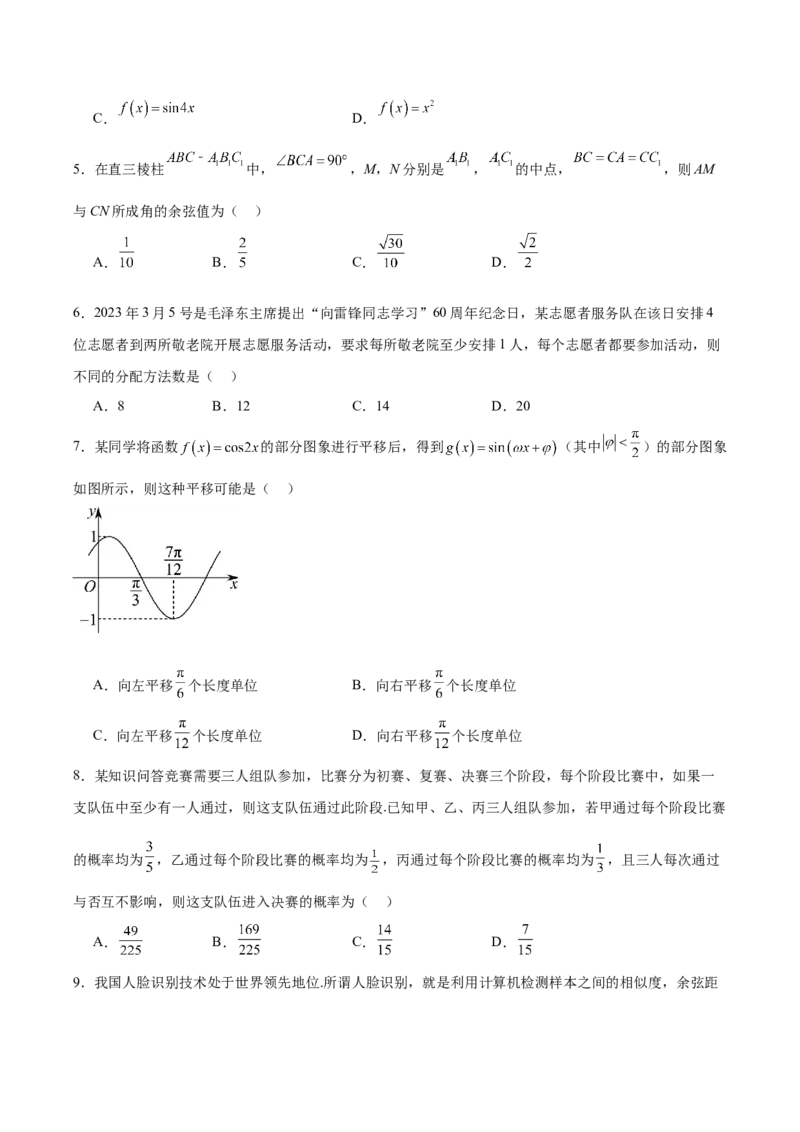
7.某同学将函数 的部分图象进行平移后,得到 (其中 )的部分图象
如图所示,则这种平移可能是( )
A.向左平移 个长度单位 B.向右平移 个长度单位
C.向左平移 个长度单位 D.向右平移 个长度单位
8.某知识问答竞赛需要三人组队参加,比赛分为初赛、复赛、决赛三个阶段,每个阶段比赛中,如果一
支队伍中至少有一人通过,则这支队伍通过此阶段.已知甲、乙、丙三人组队参加,若甲通过每个阶段比赛
的概率均为 ,乙通过每个阶段比赛的概率均为 ,丙通过每个阶段比赛的概率均为 ,且三人每次通过
与否互不影响,则这支队伍进入决赛的概率为( )
A. B. C. D.
9.我国人脸识别技术处于世界领先地位.所谓人脸识别,就是利用计算机检测样本之间的相似度,余弦距离是检测相似度的常用方法.假设二维空间中有两个点 , ,O为坐标原点,余弦相似度为
向量 , 夹角的余弦值,记作 ,余弦距离为 .已知 ,
, ,若P,Q的余弦距离为 , ,则Q,R的余弦距离为
( )
A. B. C. D.
10.函数 在区间 的图象大致为( )
A. B.
C. D.
11.已知圆 与双曲线 ,若在双曲线 上存在一点 ,使得
过点 所作的圆 的两条切线,切点为 、 ,且 ,则双曲线 的离心率的取值范围是( )
A. B.
C. D.
12. ,则( )
A. B. C. D.
第 II 卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分13.已知 , 是平面内两个不共线的非零向量, , , ,且A,
E,C三点共线,实数 .
14.双曲线 的右焦点为 ,点 在 的一条渐近线上, 为坐标原点,若 ,则
的面积为 .
15.在 中, , , , 的角平分线交 于 ,则 .
16.在正方体 中, 为棱 上的动点, 为线段 的中点.给出下列四个结论:
① ;
②直线 与平面 的夹角不变;
③三棱锥 的体积不变;
④点 到 , , , 四点的距离相等.
其中,所有正确结论的序号为
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)某校为调查高中生选修课的选修倾向与性别是否有关,随机抽取70名学生,得到如下的列
联表:
倾向“坐标系与参数方 倾向“不等式选
程” 讲”
男
15 25
生
女
20 10
生附: .
0.100 0.050 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
(1)根据表中提供的数据,判断是否有 以上的把握认为倾向“坐标系与参数方程”还是“不等式选讲”
与性别有关?
(2)在倾向“坐标系与参数方程”的学生中,按照性别采用分层抽样的方法抽取7人,再从这7人中任选3
人参与问卷调查,记3人中男生人数为 ,求 的分布列及数学期望.
18.(12分)从① , , 成等差数列;② , , 成等比数列;③ 这三个条件中任选一
个补充在下面的问题中,并解答下列问题.
已知 为数列 的前 项和, , ,且________.
(1)求数列 的通项公式;
(2)记 ,求数列 的前 项和 .
注:若选择多个条件分别解答,则按第一个解答计分.
19.(12分)如图,在三棱柱 中, , , , ,
且 平面 .
(1)求证: ;(2)求二面角 的正弦值.
20.(12分)已知椭圆 离心率等于 且椭圆C经过点 .
(1)求椭圆的标准方程 ;
(2)若直线 与轨迹 交于 两点, 为坐标原点,直线 的斜率之积等于 ,试探求
的面积是否为定值,并说明理由.
21.(12分)已知函数 .
(1)求曲线 在点 处的切线方程;
(2)若0是函数 的极小值点,求实数 的取值范围.
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.已知曲线 的参数方程分别为 ( 为参数), ( 为参数).
(1)将 的参数方程化为普通方程;
(2)以坐标原点 为极点,以 轴的非负半轴为极轴,建立极坐标系.若射线 与曲线 分别
交于 两点(异于极点),点 ,求 的面积.
选修4-5:不等式选讲
23.已知a、b均为正数,设 .
(1)当 时,求不等式 的解集;(2)若 的最小值为6,求 的值,并求 的最小值.