文档内容
2025 年全国高考数学模拟卷
命题:浙江省温州中学
考生须知:
1. 本卷满分150分,考试时间120分钟;
2. 答题前,在答题卷指定区域填写班级、姓名、试场号、座位号及准考证号。
3. 所有答案必须写在答题卷上,写在试卷上无效;
4. 考试结束后,只需上交答题卷。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合
题目要求的.请将你认为正确的答案填在答题卷的相应位置.
{ |3 ))
1.已知集合A={x∣−1≤x≤4},B= x ≤1 ,则A∩B=( ▲ )
x
A.[3,4) B.[−1,0)∪[3,4) C.(−∞,0)∪[3,+∞) D.[−1,0)
2.已知复数(1+2i)z=i2025(i是虚数单位),则|´z)=( ▲ )
❑√3 ❑√5
A. B. C.❑√3 D.❑√5
5 5
3.已知向量⃗a=(1,m+4),⃗b=(4,2),若|⃗a+⃗b)=|⃗a−⃗b),则|⃗a)=( ▲ )
A.5 B.3 C.❑√5 D.❑√3
4.函数f (x)=cos2x+2sinx在[−π,π)上的图象是( ▲ )
A. B. C. D.
5.已知圆O:x2+ y2=9,则“点M(a,b)在圆O外”是“直线ax+by=1与圆O相交”的( ▲ )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.在△ABC中,角A,B,C的对边分别为a,b,c,atanB+atanA=−2ctanA,则B=( ▲ )
π 2π π 5π
A. B. C. D.
3 3 6 6
x2 y2
7.已知双曲线C: − =1(a>0,b>0)的左、右焦点分别为F ,F ,过F 的直线与C的左、右支分
a2 b2 1 2 1
数学模拟卷·第 1 页(共 5 页)
学科网(北京)股份有限公司数学模拟卷·第 1 页(共 5 页)
别交于M,N两点,且MN⊥N F ,OM//N F ,其中O为坐标原点,则C的离心率为( ▲ )
2 2
A.5 B.❑√17 C.4 D.❑√13
8.若负实数t满足:对于任意a∈[−4,t),总存在b,c∈[−4,t),使得ab+c=1,则t的范围是( ▲
)
[ 5) [ 5 1) [ 1)
A. −4,− B. − ,− C. −❑√5,− D.[−❑√5,−4)
4 4 3 3
二、多选题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知正数a,b满足2a+b=1,则( ▲ )
1 1 2
A.ab≤ B. + ≥8
16 a b
1
C.❑√2a+❑√b≤❑√2 D.a2+b2≥
5
10.若各项为正的无穷数列{a )满足:对于∀n∈N∗,a2 −a2=d,其中d为常数,则称数列{a )为
n n+1 n n
等方差数列.那么( ▲ )
A.{2n)是等方差数列
B.若数列{a )是等方差数列,则数列{a2)是等差数列
n n
C.若数列{a )既是等方差数列,又是等差数列,则该数列为常数列
n
D.若数列{a )是等方差数列,则数列{a )(k∈N∗,k为常数)也是等方差数列
n kn
11.设函数f (x)=2(x−a) 2 (x−2),则( ▲ )
1
A.x=a是f (x)的极值点 B.当a= 时,f (2−x)+f (x)=−1
2
C.当a>2时,f (sin2x)≤f (x2) D.当a=−1时,f (sin2x)≥f (x2)
三、填空题:本大题共3小题,每小题5分,共15分.请将答案填在答题卷的相应位置.
( 1 x) 6
12.二项式 − 的展开式的常数项是 ▲ .
❑√x 3
13.已知三棱锥的侧棱两两夹角都等于60∘,三个侧面三角形的面积分别为S ,S ,S ,满足
1 2 3
数学模拟卷·第 2 页(共 5 页)
学科网(北京)股份有限公司数学模拟卷·第 2 页(共 5 页)
S =2S =2S =❑√3,则三棱锥的体积是 ▲ .
1 2 3
14.盒子中有3个红球,4个黑球,每次随机地从中取出一个球,观察其颜色后放回,并放入5个同色
球,则第三次取出红球的概率为 ▲ .
四、解答题:本大题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(13分)幸得三月樱花舞,从此阡陌多暖春.又到春暖花开时,校园的樱花如约而至.浸润在春
风里的樱花,绚烂柔美,青春美好,尽显春日浪漫.师生共赏樱花盛景,不负这盛世春光.每年樱花
季,若在樱花树下流连超10小时,则称为“樱花迷”,否则称为“非樱花迷”.从全校随机抽取30
个男生和50个女生进行调查,得到数据如表所示:
樱花迷 非樱花迷
男 5m 5
女 40 2m
(1)求m的值;
(2)根据小概率值α=0.01的独立性检验,判断“樱花迷”与性别是否有关联?
(3)现从抽取的50个女生中,用分层抽样的方法抽取10人,再从这10人中随机抽取3人,记这3人
中“非樱花迷”的人数为X,求X的分布列和数学期望.
n(ad−bc) 2
附:参考公式:χ2= ,其中n=a+b+c+d.
(a+b)(c+d)(a+c)(b+d)
α 0.10 0.05 0.01 0.005 0.001
x 2.706 3.841 6.635 7.879 10.828
α
16.(15分)已知抛物线C:y2=2px(p>0)的焦点为F,C上动点P到点F的最小距离为1.
(1)求抛物线C的标准方程;
4 |AF)
(2)过点F的直线与抛物线C交于A,B两点,O为坐标原点,S = ❑√3,求 的值.
△AOB 3 |BF)
数学模拟卷·第 3 页(共 5 页)
学科网(北京)股份有限公司数学模拟卷·第 3 页(共 5 页)
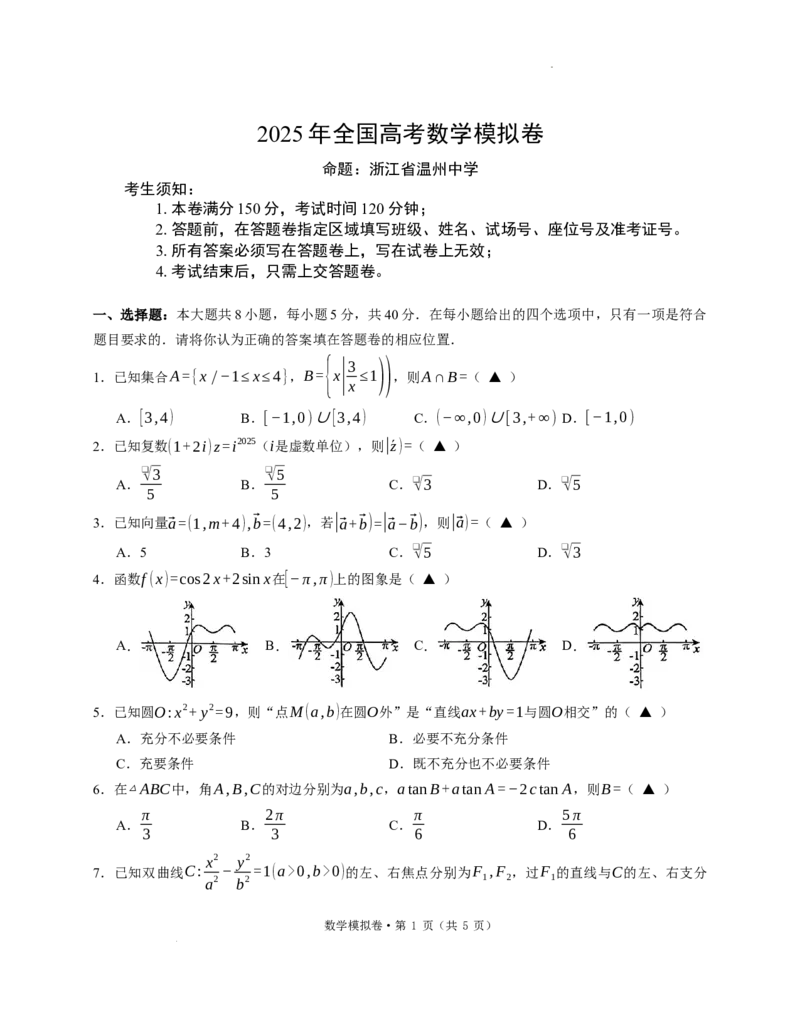
17.(15分)如图,棱长为2的正四面体A−BCD中,P为直线CD上的动点,满足⃗PD=λ⃗CD.
3
(1)若λ= ,证明:平面PAB⊥平面ABD;
2
(2)若直线CD与平面PAB所成夹角为45∘,求线段PA的长度.
18.(17分)已知函数f (x)=(x+a)ln(x+1)(a∈R),g(x)=lnx−bx(b>0).
(1)若a=2,求曲线y=f (x)在点(0,f (0))处的切线方程;
(2)当x>0时,f (x)>2x恒成立,求实数a的取值范围;
2
(3)若存在x ,x ∈(0,+∞),使得g(x )=g(x )(x ≠x ).证明:❑√x +❑√x > .
1 2 1 2 1 2 1 2 ❑√b
19.(17分)对于一个严格递增的无穷正整数数列{a ),如果对每个正整数n,这个数列前a 项的平均
n n
数为a ,则称这个数列是“中立的”.数列{b )的通项公式为b =2n−1(n∈N ).
n n n +
(1)证明:数列{b )是“中立的”;
n
数学模拟卷·第 4 页(共 5 页)
学科网(北京)股份有限公司数学模拟卷·第 4 页(共 5 页)
(2)证明:对于任意一个“中立的”数列{a ),对任意正整数n,均有
n
a +a +⋯+a =b +b +⋯+b ;
a +1 a +2 a a +1 a +2 a
n n n+1 n n n+1
(3)证明:对于任意一个“中立的”数列{a ),均存在无穷多个正整数n,使得a =b .
n n n
数学模拟卷·第 5 页(共 5 页)
学科网(北京)股份有限公司