文档内容
绝密★启用前
2024年普通高等学校招生全国统一考试
文科数学试题卷
( 银川一中第二次模拟考试 )
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,务必将答案写在答题卡上。写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.已知集合 ,则
A. B.
C. D.
2.已知 ,若 为纯虚数,则
A. B.2 C.1 D.
3.我国有着丰富悠久的“印章文化”,古时候的印章一般用贵重的金属或玉石制成,本
是官员或私人签署文件时代表身份的信物,后因其独特的文化内涵,也被作为装饰物来
使用.图1是明清时期的一个金属印章摆件,除去顶部的环以后可以看作是一个正四棱
柱和一个正四棱锥组成的几何体,如图2.已知正四棱柱和正四棱锥的高相等,且底面
边长均为4,若该几何体的所有顶点都在同一个球面上,则这个球的表面积是
A. B. C. D.
文数学试卷 第1页(共3页)
学科网(北京)股份有限公司4.已知函数 为奇函数,则 的值是
A. B. C. D.
5.设O为平面直角坐标系的坐标原点,在区域 内随机取一点,记该点
为A,则点A落在区域 内的概率为
A. B. C. D.
6.已知向量 满足 , , ,则
A. B. C. D.
7.已知 为等比数列 的前 项和,且公比 ,则“ ”是“ ”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
8.若 ,则
A. B. C. D.
9.过双曲线 的左焦点 作圆 的切线,切点
为 ,延长 交双曲线右支于点 , 为坐标原点,若 为 的中点,则双曲线的
离
心率为
A. B. C. D.
10.已知 为直线 上的动点,点 满足 ,记 的轨迹为
,
则
A. 是一个半径为 的圆 B. 是一条与 相交的直线
C. 上的点到 的距离均为 D. 是两条平行直线
文数学试卷 第2页(共3页)
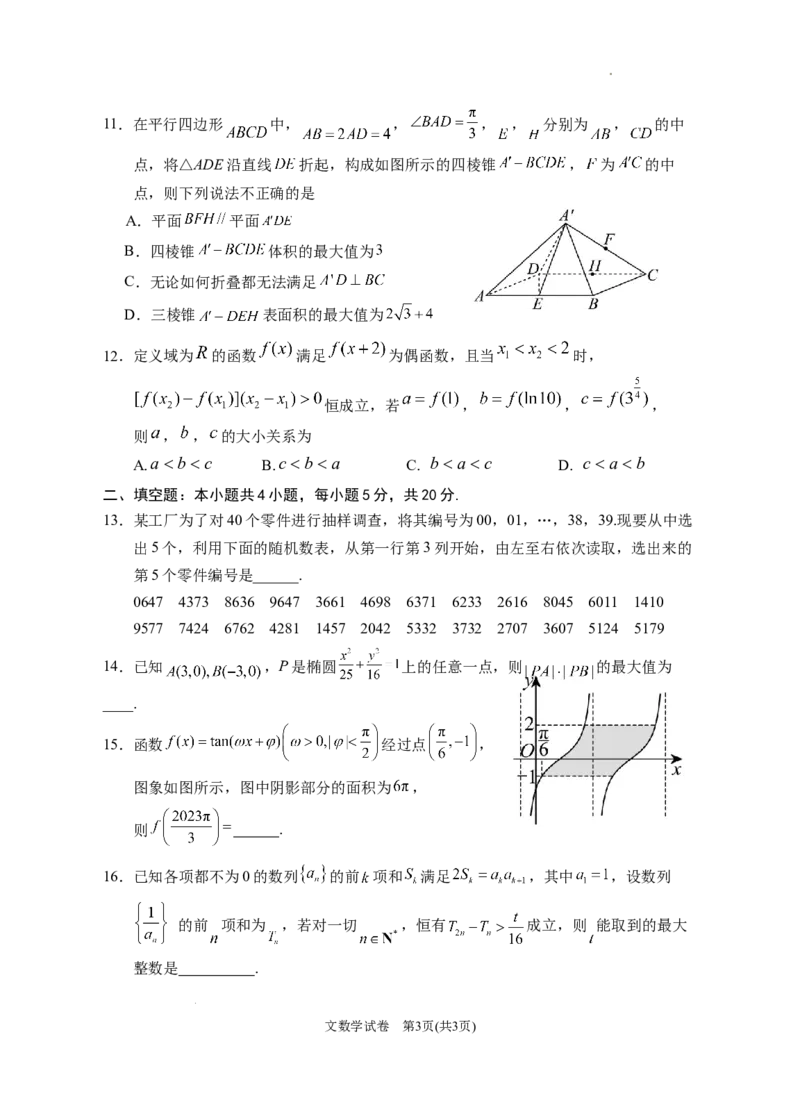
学科网(北京)股份有限公司11.在平行四边形 中, , , , 分别为 , 的中
点,将△ADE沿直线 折起,构成如图所示的四棱锥 , 为 的中
点,则下列说法不正确的是
A.平面 平面
B.四棱锥 体积的最大值为
C.无论如何折叠都无法满足
D.三棱锥 表面积的最大值为
12.定义域为 的函数 满足 为偶函数,且当 时,
恒成立,若 , , ,
则 , , 的大小关系为
A.a bc B.c b a C. b a c D. c a b
二、填空题:本小题共4小题,每小题5分,共20分.
13.某工厂为了对40个零件进行抽样调查,将其编号为00,01,…,38,39.现要从中选
出5个,利用下面的随机数表,从第一行第3列开始,由左至右依次读取,选出来的
第5个零件编号是______.
0647 4373 8636 9647 3661 4698 6371 6233 2616 8045 6011 1410
9577 7424 6762 4281 1457 2042 5332 3732 2707 3607 5124 5179
14.已知 ,P是椭圆 上的任意一点,则 的最大值为
____.
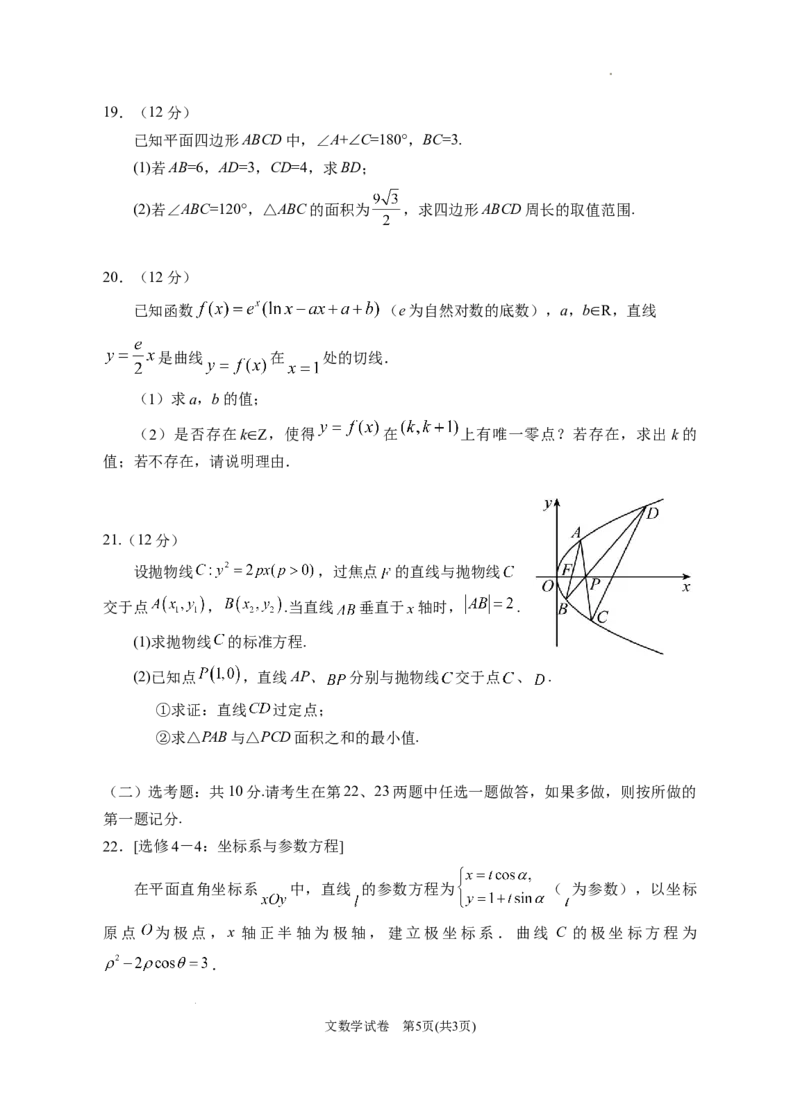
15.函数 经过点 ,
图象如图所示,图中阴影部分的面积为 ,
则 .
16.已知各项都不为0的数列 的前 项和 满足 ,其中 ,设数列
的前 项和为 ,若对一切 ,恒有 成立,则 能取到的最大
整数是 .
文数学试卷 第3页(共3页)
学科网(北京)股份有限公司三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考
题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分)
17.(12分)
某蛋糕店计划按天生产一种面包,每天生产量相同,生产成本每个6元,售价每个8
元,未售出的面包降价处理,以每个5元的价格当天全部处理完.
(1)若该蛋糕店一天生产30个这种面包,求当天的利润y(单位:元)关于当天需
求量n(单位:个, )的函数解析式;
(2)蛋糕店记录了30天这种面包的日需求量(单位:个),整理得表:
2 3
日需求量n 29 30 31 33
8 2
频数 3 4 6 6 7 4
假设蛋糕店在这30天内每天生产30个这种面包,求这30天的日利润(单位:元)
的平均数及方差.
18.(12分)
如图,已知三棱柱 的底面是边长为2的
正三角形,侧面 为菱形, 为其两对角线的交点,
, , 、 分别为 、 的
中点,顶点 在底面 的射影 为底面中心.
(1)求证: 平面 ,且 平面 ;
(2)求三棱锥 与三棱柱 的体积之比.
文数学试卷 第4页(共3页)
学科网(北京)股份有限公司19.(12分)
已知平面四边形ABCD中,∠A+∠C=180°,BC=3.
(1)若AB=6,AD=3,CD=4,求BD;
(2)若∠ABC=120°,△ABC的面积为 ,求四边形ABCD周长的取值范围.
20.(12分)
已知函数 (e为自然对数的底数),a,b∈R,直线
是曲线 在 处的切线.
(1)求a,b的值;
(2)是否存在k∈Z,使得 在 上有唯一零点?若存在,求出k的
值;若不存在,请说明理由.
21.(12分)
设抛物线 ,过焦点 的直线与抛物线
交于点 , .当直线 垂直于 轴时, .
(1)求抛物线 的标准方程.
(2)已知点 ,直线AP、 分别与抛物线 交于点 、 .
①求证:直线 过定点;
②求△PAB与△PCD面积之和的最小值.
(二)选考题:共10分.请考生在第22、23两题中任选一题做答,如果多做,则按所做的
第一题记分.
22.[选修4-4:坐标系与参数方程]
在平面直角坐标系 中,直线 的参数方程为 ( 为参数),以坐标
原点 为极点,x 轴正半轴为极轴,建立极坐标系.曲线 C 的极坐标方程为
.
文数学试卷 第5页(共3页)
学科网(北京)股份有限公司(1)求曲线C的直角坐标方程和直线 的一般方程;
(2)设直线 与曲线C交于A、B两点,求△ABC面积的最大值.
23.[选修4-5:不等式选讲]
已知函数 , .
(1)当 时,解不等式 ;
(2)若 对任意 恒成立,求 的取值范围.
文数学试卷 第6页(共3页)
学科网(北京)股份有限公司