文档内容
2024 年 1 月“九省联考”考后提升卷
高三数学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,
用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上
无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.现有一组数据: ,则这组数据的第85百分位
数是( )
A.652 B.668 C.671 D.674
【答案】C
【解析】
【分析】根据百分位数的定义,求得 ,即可确定第85百分位数为第11个数,可得
答案.
【详解】由题意这组数共12个,则 ,
为
将这组数据从小到大排列 ,
故这组数据的第85百分位数为第11个数,即671,故选:C
2.已知椭圆 的上顶点、右顶点、左焦点恰好是等腰三角形的三个顶点,则
椭圆C的离心率为( )A. B. C. D.
2.【答案】D【解析】易知等腰三角形的三边为 ;则 即有
,解得e ,故选:D.
3.已知 为数列 的前 项和,且满足 ,则 ( )
A. B. C. D.
【答案】A
【解析】
【分析】由题,当 时, ,当 时 ,进而分奇偶性讨论得
, 为正偶数, , 为正奇数,再求和即可.
【详解】解:因为 ,
所以,当 时, ,解得 ,
当 时, ,
所以,当 为偶数时, ,故 , 为正奇数;
当 为奇数时, ,即 ,故 , 为正偶数;
所以 ,
故选:A4..已知 , 为异面直线,直线 与 , 都垂直,则下列说法不正确的是( )
A.若 平面 ,则 ,
B.存在平面 ,使得 , ,
C.有且只有一对互相平行的平面 和 ,其中 ,
D.至少存在两对互相垂直的平面 和 ,其中 ,
【答案】A
【分析】由线面关系判断ABD;由线面垂直判定判断C;
【详解】对于A,如下图所示,在正方体中取 为 , 为 , 为 ,平面 为平面
,则 , ,故A错误;
对于B,在正方体中取 为 , 为 , 为 ,平面 为平面 ,此时 , ,
,故B正确;
对于C,由线面垂直的判定可知, , ,过直线 且与 垂直的平面只有一个,过直线
且与 垂直的平面只有一个,则有且只有一对互相平行的平面 和 ,其中 , ,故C
正确;
对于D,在正方体中取 为 , 为 , 为 ,此时平面 平面 ,平面
平面 ,即至少存在两对互相垂直的平面 和 ,其中 , ,故D正确;故选:A.
5.某学校举办运动会,径赛类共设100米、200米、400米、800米、1500米5个项目,田赛类共设铅
球、跳高、跳远、三级跳远4个项目.现甲、乙两名同学均选择一个径赛类项目和一个田赛类项目参
赛,则甲、乙的参赛项目有且只有一个相同的方法种数等于( )
A.70 B.140 C.252 D.504
【答案】B
【分析】由分类加法、分步乘法计数原理以及排列组合的计算即可得解.
【详解】由题意若甲、乙的相同的参赛项目为径赛类项目,则有 种选法,
他们再分别从田赛类项目中各选一个(互不相同)即可,这时候有 种选法,
所以此时满足题意的选法有 ,
由题意若甲、乙的相同的参赛项目为田赛类项目,则有 种选法,
他们再分别从径赛类项目中各选一个(互不相同)即可,这时候有 种选法,
所以此时满足题意的选法有 ,
.
综上所述,甲、乙的参赛项目有且只有一个相同的方法种数等于 种.故选:B
6.在棱长为1的正方体 中, 在侧面 (含边界)内运动, 在底面
(含边界)内运动,则下列说法不正确的是( )
A. 若直线 与直线 所成角为30°,则 点的轨迹为圆弧B. 若直线 与平面 所成角为30°,则 点的轨迹为双曲线的一部分
C. 若 ,则 点的轨迹为线段
D. 若 到直线 的距离等于 到平面 的距离,则点 的轨迹为抛物线的一部分
【答案】C
【解析】
【分析】画出正方体 ,根据各选项的不同条件对图形进行分析并运算即可得出轨
迹问题的结论.
【详解】直线 与直线 所成角即为 ,在 中, ,∴ ,故
在以 为圆心, 为半径的圆落在侧面 内的圆弧上,A正确;
过 作 于点 (如图),设 , ,直线 与平面 所成角即为 ,
在 中, ,从而 ,故点 的轨迹为双曲线的一部
分,故B正确;
在 中, ,从而 ,故 在以 为圆心, 为半径的圆落
在底面 内的圆弧上,C错误;到直线 的距离等于 到平面 的距离,即 到点 的距离等于 到直线 的距离,
故点 的轨迹为抛物线的一部分,故D正确.
故选:C.
7.已知角 的终边上一点 的坐标为 ,则 的值为( )
A.0 B. C. D.
【答案】B
【分析】根据三角函数的定义求出 ,再根据两角和的正切公式展开代入化简求解.
【详解】角 的终边上一点 的坐标为
所以 ,则 ,故选:B
8.已知 , 分别为双曲线 : 的左,右焦点,点P为双曲线渐近线上一
点,若 , ,则双曲线 的离心率为( )
A. B. C. D. 2
【答案】B
【解析】
【分析】由题可得 ,然后利用二倍角公式结合条件可得 ,然后根据离心率
公式即得.【详解】因为 , 为 的中点,
所以 , ,
所以 ,又 , ,
所以 ,
所以 .
故选:B.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.将函数 的图象向左平移 个单位长度,再将图象上所有点的横坐标变为原来的 倍
(纵坐标不变),得到 的图象,则( )
A. 函数 是偶函数
B. x=- 是函数 的一个零点C. 函数 在区间 上单调递增
D. 函数 的图象关于直线 对称
【答案】BCD
【解析】
【分析】首先求出 的解析式,然后根据正弦函数的性质逐一判断即可.
【详解】将函数 的图象向左平移 个单位长度,可得 ,
再将图象上所有点的横坐标变为原来的 倍(纵坐标不变),可得 ,
对于A选项,令 ,
则 , ,故函数 不是偶函数,A不正确;
对于B选项,因为 ,故 是函数 的一个零点,B正确;
对于C选项,当 时, ,所以函数 在区间 上单调递增,
C正确;
对于D选项,因为对称轴满足 ,解得 ,
则 时, ,所以函数 的图象关于直线 对称,D正确.
故选:BCD.
10.已知z 与z 是共扼复数,以下四个命题一定是正确的是( )
1 2A. B. C. D.
【答案】BC
【分析】设 ,分别求出 ,得到A不正确;根据复数的运算,可得B
正确;根据 ,可得C正确;根据复数的除法运算,可得D不一定正确,即可求解.
【详解】设 ,
则 , ,所以A不正确;
又由 , ,所以 ,所以B正确;
由 ,所以C正确;
由 不一定是实数,所以D不一定正确.
故选:BC
11.已知定义在 上的函数 满足 ,且 为奇函数,则下列说法一定
正确的是( )
A. 函数 的周期为
B. 函数 的图象关于 对称
C. 函数 为偶函数
D. 函数 的图象关于 对称
【答案】BC
【解析】【分析】由 得函数 的一个周期,由 是奇函数得函数的对称中心,
两条件结合得函数 的奇偶性.
【详解】由 ,得 ,
将 代入, ,即 ,
所以函数 的一个周期为7,A项错误;
由 是奇函数得 ,
因为 和 ,
所以 ,
即 ,所以 的图象关于 中心对称,B项正确,D项错误;
因为 , ,
所以 ,将 代入,
得 ,即函数 为偶函数,C项正确.
故选:BC.
三、填空题:本题共3小题,每小题5分,共15分.
12.已知集合 ,若 ,且 ,则实数 的取值范围是
__________.
【答案】【解析】
【分析】先解分式不等式,即可得出集合 ,再由 ,且 ,即可求出实数 的
取值范围.
详解】由 可得: ,解得: ,
【
所以 ,
因为 ,且 ,
所以 .
故答案为: .
13.甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为 ,侧面积分别为 和 ,体积
分别为 和 .若 ,则
【答案】
【分析】设母线长为 ,甲圆锥底面半径为 ,乙圆锥底面圆半径为 ,根据圆锥的侧面积公式可
得 ,再结合圆心角之和可将 分别用 表示,再利用勾股定理分别求出两圆锥的高,再
根据圆锥的体积公式即可得解.
【详解】解:设母线长为 ,甲圆锥底面半径为 ,乙圆锥底面圆半径为 ,
则 ,所以 ,
又 ,则 ,所以 ,所以甲圆锥的高 ,
乙圆锥的高 ,
所以 .
14.已知数列 满足 , ,则 的前 项积的最大值为
【答案】1
【分析】先通过递推关系推出数列的周期为 ,然后 个数为一组,分别计算 的表达
式 后进行研究.
【详解】由 可知, , ,亦可得: ,两式相除得:
,即 ,所以数列 是以 为周期的周期数列,由 得:
.
记数列 的前 项积为 ,结合数列的周期性,当 ,则 ,记
,为了让 越大,显然需考虑 为偶数,令 ,结合指数函数的单调性,则,即 ;类似的 ,
.综上所述, 的前 项积的最大值为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)设函数 , , ,已知曲线 在点
处的切线与直线 垂直.
(1)求a的值;
(2)求 的单调区间;
【答案】(1)2 (2)答案见解析
【解析】
的
【分析】(1)利用导数 几何意义可得关于a的方程,解方程即可得出答案;
(2)对 求导,分 和 讨论 的正负,即可求出 的单调性;
【小问1详解】
的定义域为 ,
,
由于直线 的斜率为 , . 6分
【小问2详解】
, ,
①当 时, , 在R上单调递增;
②当 时,令 有 ,当 时, , 单调递减,
当 时, , 单调递增.
综上所述: , 的单调递增区间为R,
, 的单调减区间为 , 的单调增区间为 . 13分
【点睛】关键点点睛:本题考查导数的几何意义、求单调区间和利用导数求解恒成立问题;本题
求解恒成立问题的关键是将恒成立问题转化为求函数的最值.
16.(15分)为倡导公益环保理念,培养学生社会实践能力,某中学开展了旧物义卖活动,所得
善款将用于捐赠“圆梦困境学生”计划.活动共计50多个班级参与,1000余件物品待出售.摄影社
从中选取了20件物品,用于拍照宣传,这些物品中,最引人注目的当属优秀毕业生们的笔记本,
已知高三1,2,3班分别有 的同学有购买意向.假设三个班的人数比例为6:7:8
(1)现从三个班中随机抽取一位同学:
(i)求该同学有购买意向的概率;
(ii)如果该同学有购买意向,求此人来自2班的概率;
(2)对于优秀毕业生的笔记本,设计了一种有趣的“掷骰子叫价确定购买资格”的竞买方式:统一
以0元为初始叫价,通过掷骰子确定新叫价,若点数大于2,则在已叫价格基础上增加1元更新叫
价,若点数小于3,则在已叫价格基础上增加2元更新叫价;重复上述过程,能叫到10元,即获
得以10元为价格的购买资格,未出现叫价为10元的情况则失去购买资格,并结束叫价.若甲同学
已抢先选中了其中一本笔记本,试估计其获得该笔记本购买资格的概率(精确到0.01).
【答案】(1)(i) (2)0.75.
【分析】(1)设事件 “该同学有购买意向”,事件 “该同学来自i班”(i=1,2,3).根据全概率
公式即可求解 ,根据条件概率公式即可求解
(2)由题意可得每次叫价增加1元的概率为 ,每次叫价增加2元的概率为 .设叫价为 元的概率为 ,叫价出现 元的情况只有下列两种:①叫价为 元,且骰子点数大于2,其概率为
②叫价为 元,且骰子点数小于3,其概率为 .于是得到 ,构
造等比数列 ,结合累加法可求解。
【详解】(1)(i)设事件A=“该同学有购买意向”,事件Bi=“该同学来自i班”
由题意可知 ,
所以,由全概率公式可得
8分
(2)由题意可得每次叫价增加1元的概率为 ,每次叫价增加2元的概率为 .
设叫价为 元的概率为 ,叫价出现 元的情况只有下列两种:
①叫价为 元,且骰子点数大于2,其概率为
②叫价为 元,且骰子点数小于3,其概率为
于是得到 ,易得
由于
于是当 时,数列 是以首项为 公比为 的等比数列,故 .
于是 =
$
于是,甲同学能够获得笔记本购买资格的概率约为0.75. 15分
【点睛】关键点睛:
第二问中关键是设叫价为 元的概率为 ,利用叫价为 元是在叫价为 元的基础上
再叫价1元或在叫价为( 元的基础上再叫价2元,从而确定 与 的关系,再结合数列中的
构造法和累加法即可求解.
17.(15分)如图,在多面体 中,底面 为菱形, 平面 ,
,且 为棱 的中点, 为棱 上的动点.
(1)求二面角 的正弦值;
(2)是否存在点 使得 平面 ?若存在,求 的值;否则,请说明理由.
【答案】(1) ;(2)存在, .
【解析】
【分析】(1)连接 交于点 ,作 平面 ,以 为原点建立空间直角坐标系,利
用面面角的向量求法求解即得.
(2)利用(1)中信息,假定存在符合条件的点 ,利用空间位置关系的向量证明求解即得.
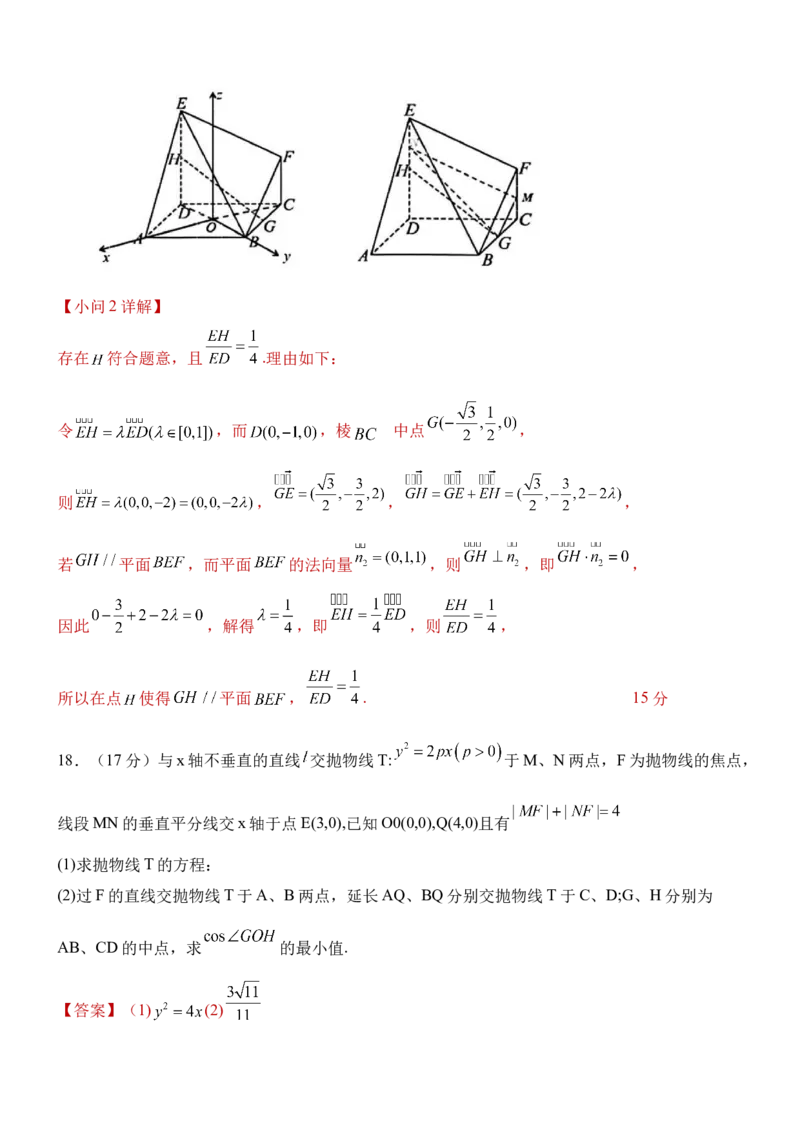
【小问1详解】
连接 交于点 ,由四边形 为菱形,得 ,过点 作 平面 ,
显然直线 两两垂直,以 为原点,直线 分别为 建立空间直角坐标系,
由 平面 ,得 ,又 ,且 ,
则 ,
,
设平面 ,平面 的法向量分别为 ,
则 ,取 ,得 ,
则 ,取 ,得 ,
设二面角 的大小为 ,则 ,
因此 ,所以二面角 的正弦值为 . 8分【小问2详解】
存在 符合题意,且 .理由如下:
令 ,而 ,棱 中点 ,
的
则 , , ,
若 平面 ,而平面 的法向量 ,则 ,即 ,
因此 ,解得 ,即 ,则 ,
所以在点 使得 平面 , . 15分
18.(17分)与x轴不垂直的直线 交抛物线T: 于M、N两点,F为抛物线的焦点,
线段MN的垂直平分线交x轴于点E(3,0),已知O0(0,0),Q(4,0)且有
(1)求抛物线T的方程:
(2)过F的直线交抛物线T于A、B两点,延长AQ、BQ分别交抛物线T于C、D;G、H分别为
AB、CD的中点,求 的最小值.
【答案】(1) (2)【解析】
(1)设M ,N ,由抛物线定义可知 ,又线段MN的垂直平分线
交x轴于点E(3,0),故|ME|=|NE|,
即( = =2
因为 ,所以( ,即 ,则有 ,
即抛物线T的方程为 . 7分
(2)设
代入 得 ,则有 ,
所以 ,故
设C( ,D( ,则 解得 ,同理, ,
所以H点的横坐标为
H点的纵坐标为 ,所以 ,有 , 9分
记 ,故 ,
当 时, =0,
当 时, ,易求得 取直线OG、OH的方向向量分别为 ,
故cos 13分
当 时, ,当 时,
函数 在区间 上单调递减,最小值为 ,
所以当 时, 取到最小值为 17分
19.(17分)对于无穷数列{a },设集合A={x|x=a ,n≥1}.若A为有限集,则称数列{a }为“T
n n n
数列”.
1
(1)已知数列{a }满足a =2,a = ,判断{a }是否为“T数列”,并说明理由;
n 1 n+1 1−a n
n
(2)设函数y=f(x)的表达式为f(x)=3|x+1|−|x+2|,数列{a }满足a =f (a ).若{a }为“T数
n n+1 n n
列”,求首项a 的值;
1
(3)设a =cos(tπn).若数列{a }为“T数列”,求实数t的取值集合.
n n
1
【解题思路】(1)根据a =2,a = ,计算即可;(2)f(x) =f(−1)=−1,当x>−1时,
1 n+1 1−a min
n
f(x)=2x+1>x,分a =−1,a ≠−1两种情况讨即可;(3)当t为有理数时,必存在p∈Z+,q∈Z,
1 1
q [q ] (q ) q
使得t= ,则a =cos π(n+2p) =cos πn+2qπ =cos πn=a ,因此集合
p n+2p p p p n
A={x|x=a ,n∈N∗}中元素个数不超过2p,为有限集;t为无理数时,用反证法证明a ≠a 解决即
n m n
可.1
【解答过程】(1)因为a =2,a = ,
1 n+1 1−a
n
1 1 1 1 1
a = =−1,a = = ,a = =2,a = =−1
所以 2 1−2 3 1+1 2 4 1 5 1−2 ,
1−
2
{ 1 }
所以A={x|x=a ,n∈N∗}= −1, ,2 ,所以{a }是“T数列”; 5分
n 2 n
(2)由题知,f(x)=3|x+1|−|x+2|=¿,
所以f(x) =f(−1)=−1,
min
当x>−1时,f(x)=2x+1>x(∗),
因此当a =−1时,a =f (a )=−1,a =f (a )=−1,⋯,
1 2 1 3 2
即a =−1,n∈N∗,此时{a }为“T数列”,
n n
当a ≠−1时,a =f (a )>−1,
1 2 1
由(∗)得a =f (a )>a >−1,a =f (a )>a >−1,...,
3 2 2 4 3 3
因此a >a ,{a }显然不是“T数列”;
n+1 n n
综上,a =−1; 9分
1
q
(3)当t为有理数时,必存在p∈Z+,q∈Z,使得t= ,
p
[q ] (q ) q
则a =cos π(n+2p) =cos πn+2qπ =cos πn=a ,
n+2p p p p n
因此集合A={x|x=a ,n∈N∗}中元素个数不超过2p,为有限集;
n
当t为无理数时,对任意m,n∈N∗,m≠n,下用反证法证明a ≠a ,
m n
若a =a ,即costπn=costπm,
m n
则tπn=tπm+2kπ或tπn=−tπm+2kπ,其中k∈Z,
2k 2k
则t= ∈Q或t= ∈Q,矛盾,所以a ≠a ,
n−m n+m m n
因此集合A={x|x=a ,n∈N∗}必为无限集;
n
综上,t的取值集合是全体有理数,即t∈Q. 17分