2024年初东北育才学校高中部第六次模拟考试数学试题_2024年3月_013月合集_2024届辽宁省东北育才学校高三下第六次模拟考试

2023-2024 学年度东北育才学校高中部高三年级第六次模 拟考试暨假期质量测试数学科试卷 答题时间：120 分钟 满分：150 分 命题人：高三备课组 一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中项是 符合题目要求的． A  x x2 5x60  B  x y ln2x14 ð A B 1. 若集合 ， ，则 R （ ） A. 7, B. 6, C. 1,7 D. 1,6 1 2.已知xR，则“|x1||x1|2”是“ 1”的（ ） x A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 3. 在x1n 的二项展开式中，仅有第4项的二项式系数最大，则n（ ） A. 5 B. 6 C. 7 D. 8 3 4.若 f x 是R 上周期为3的偶函数，且当0 x 时， f xlog x，则 2 4  13 f    （ ）  2  1 1 A.  B. C. 2 D. 2 2 2 π π π  1 5. 若  , ，且cos2cos  2   ．则tan（ ） 4 2 2  2 A. 3 B. 2 C. 3 D. 2 3 1 6. 函数 f x 2cos  x2023π 在区间[3,5]上所有零点的和等于 x1 （ ） A. 2 B. 4 C. 6 D. 8 高三年级数学科试卷 第1页 共7页 学科网（北京）股份有限公司x2 y2 7. F,F 是双曲线E:  1a,b0的左、右焦点，点M 为双曲线E右支上一 1 2 a2 b2 点 ， 点 N 在 x轴 上 ， 满 足 FMN F MN 60o， 若 1 2 uuuur uuuur uuuur 3MF 5MF MNR，则双曲线E的离心率为 （ ） 1 2 8 6 5 7 A. B. C. D. 7 5 3 2 8．设S 是一个无穷数列a 的前n项和，若一个数列满足对任意的正整数n，不等式 n n S S n  n1 恒成立，则称数列a 为和谐数列，有下列3个命题： n n1 n ①若对任意的正整数n均有a a ，则a 为和谐数列； n n1 n ②若等差数列a 是和谐数列，则S 一定存在最小值； n n ③若a 的首项小于零，则一定存在公比为负数的一个等比数列是和谐数列． n 以上3个命题中真命题的个数有 （ ）个 A．3 B．2 C．1 D．0 二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符 合题目要求。全部选对的得6分，部分选对的得部分分，有选错的得0分。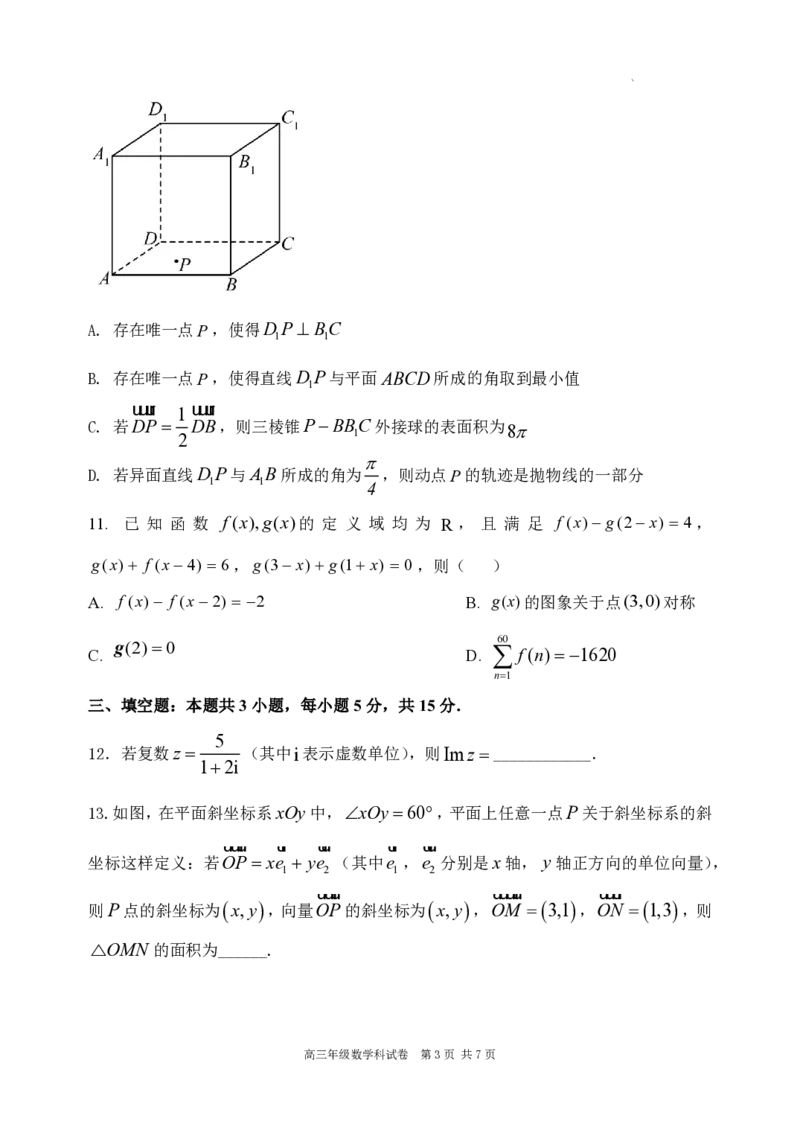 9.下列命题中，真命题有（ ）  1 4 A.若随机变量X ~B6, ，则DX=  3 3 B.数据6，2，3，4，5，7，8，9，1，10的70%分位数是8.5 X ~ N  2,2 PX 10.68 C.若随机变量 ， ，则P2 x30.28 D.若事件A,B满足 0 P(A),P(B)1 且PABPA  1PB ，则A与B独立 10. 如图，在正方体ABCDABC D 中，AB2，P是正方形ABCD内部(含边界) 1 1 1 1 的一个动点，则（ ） 高三年级数学科试卷 第2页 共7页 学科网（北京）股份有限公司A. 存在唯一点P，使得DP BC 1 1 B. 存在唯一点P，使得直线DP与平面ABCD所成的角取到最小值 1 uuur uuur 1 C. 若DP 2 DB，则三棱锥PBB 1 C外接球的表面积为8  D. 若异面直线DP与AB所成的角为 ，则动点P的轨迹是抛物线的一部分 1 1 4 11. 已 知 函 数 f(x),g(x)的 定 义 域 均 为 R ， 且 满 足 f (x) g(2 x)  4， g(x) f (x4)  6，g(3 x) g(1 x)  0，则（ ） A. f (x) f (x2)  2 B. g(x)的图象关于点(3,0)对称 60 g(2)0 C. D. 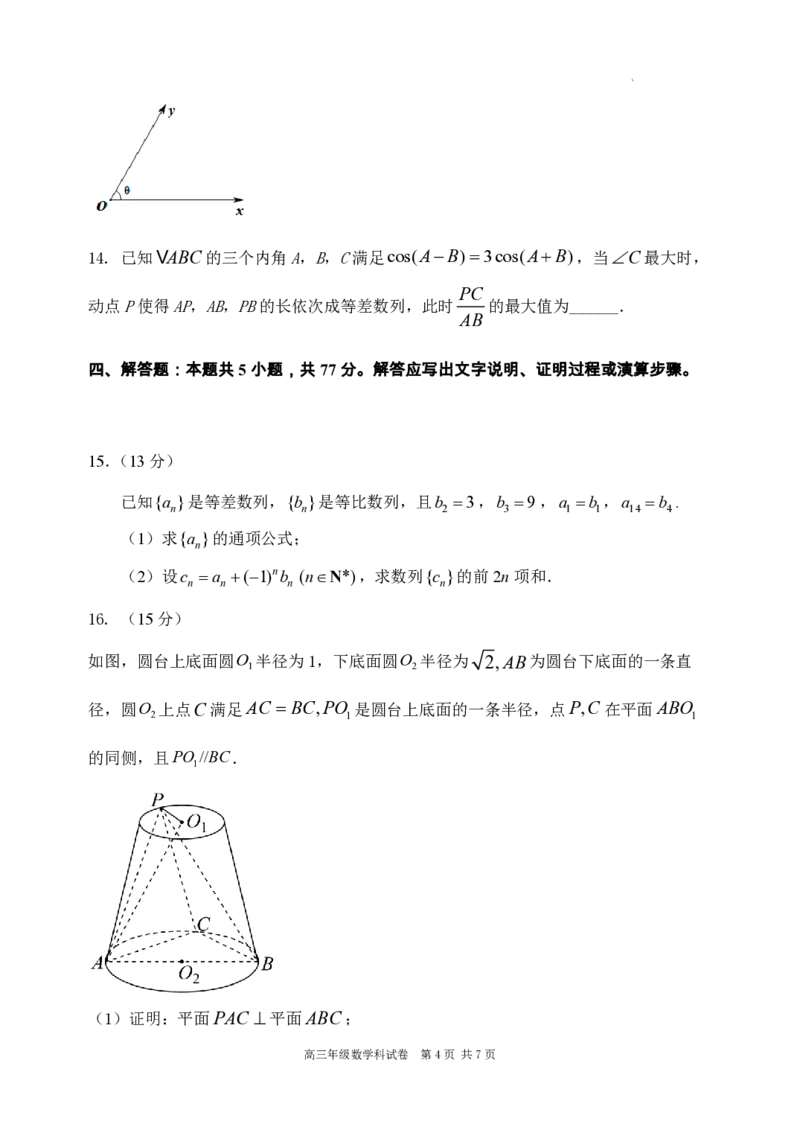 f(n)1620 n1 三、填空题：本题共3小题，每小题5分，共15分． 5 12．若复数z  （其中i表示虚数单位），则Imz ____________． 12i 13.如图，在平面斜坐标系xOy中，xOy 60，平面上任意一点P关于斜坐标系的斜 uuur ur uur ur uur 坐标这样定义：若OP xe  ye （其中e ，e 分别是x轴， y轴正方向的单位向量）， 1 2 1 2 uuur uuuur uuur 则P点的斜坐标为x,y，向量OP的斜坐标为x,y，OM 3,1，ON 1,3，则 △OMN 的面积为______. 高三年级数学科试卷 第3页 共7页 学科网（北京）股份有限公司14. 已知VABC的三个内角A，B，C满足cos(AB)3cos(AB)，当C最大时， PC 动点P使得AP，AB，PB的长依次成等差数列，此时 的最大值为______． AB 四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 15．（13分） 已知{a }是等差数列，{b }是等比数列，且b 3，b 9，a b ，a b . n n 2 3 1 1 14 4 （1）求{a }的通项公式； n （2）设c a (1)nb (nN*)，求数列{c }的前2n项和． n n n n 16. 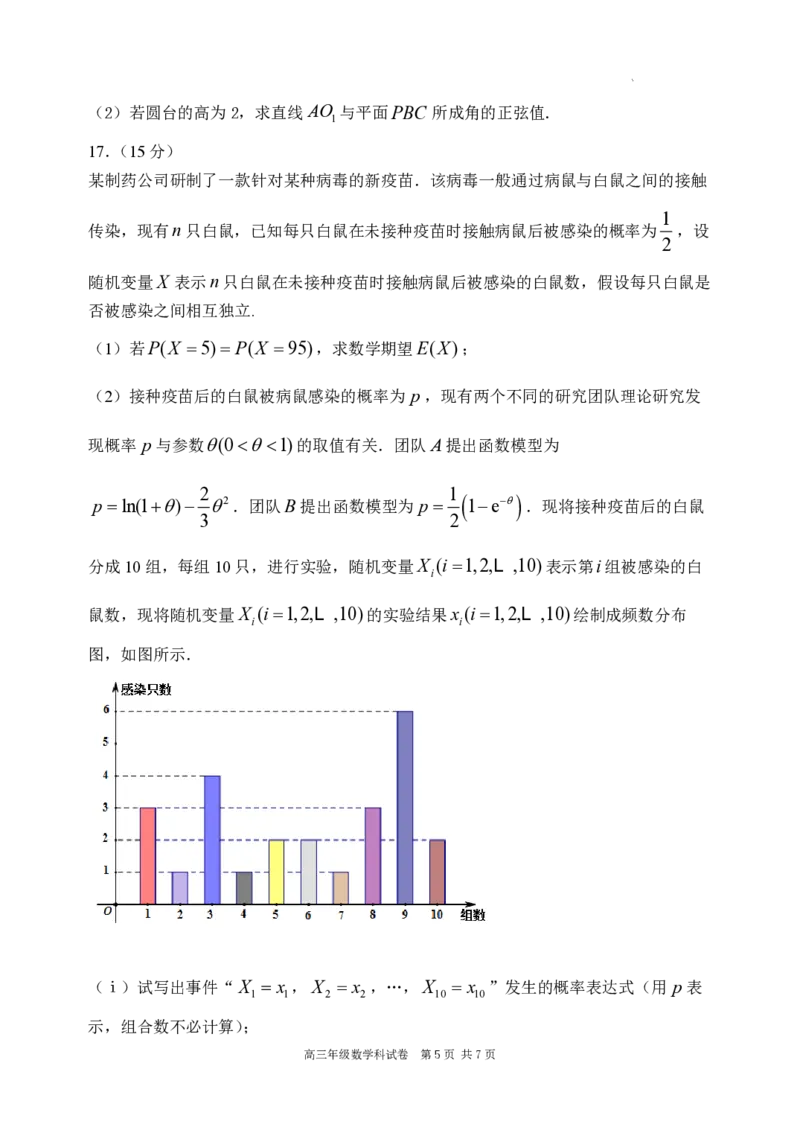（15分） 如图，圆台上底面圆O 半径为1，下底面圆O 半径为 2,AB为圆台下底面的一条直 1 2 径，圆O 上点C满足AC  BC,PO 是圆台上底面的一条半径，点P,C 在平面ABO 2 1 1 的同侧，且PO //BC. 1 （1）证明：平面PAC 平面ABC； 高三年级数学科试卷 第4页 共7页 学科网（北京）股份有限公司（2）若圆台的高为2，求直线AO 与平面PBC 所成角的正弦值. 1 17．（15分） 某制药公司研制了一款针对某种病毒的新疫苗．该病毒一般通过病鼠与白鼠之间的接触 1 传染，现有n只白鼠，已知每只白鼠在未接种疫苗时接触病鼠后被感染的概率为 ，设 2 随机变量X 表示n只白鼠在未接种疫苗时接触病鼠后被感染的白鼠数，假设每只白鼠是 否被感染之间相互独立. 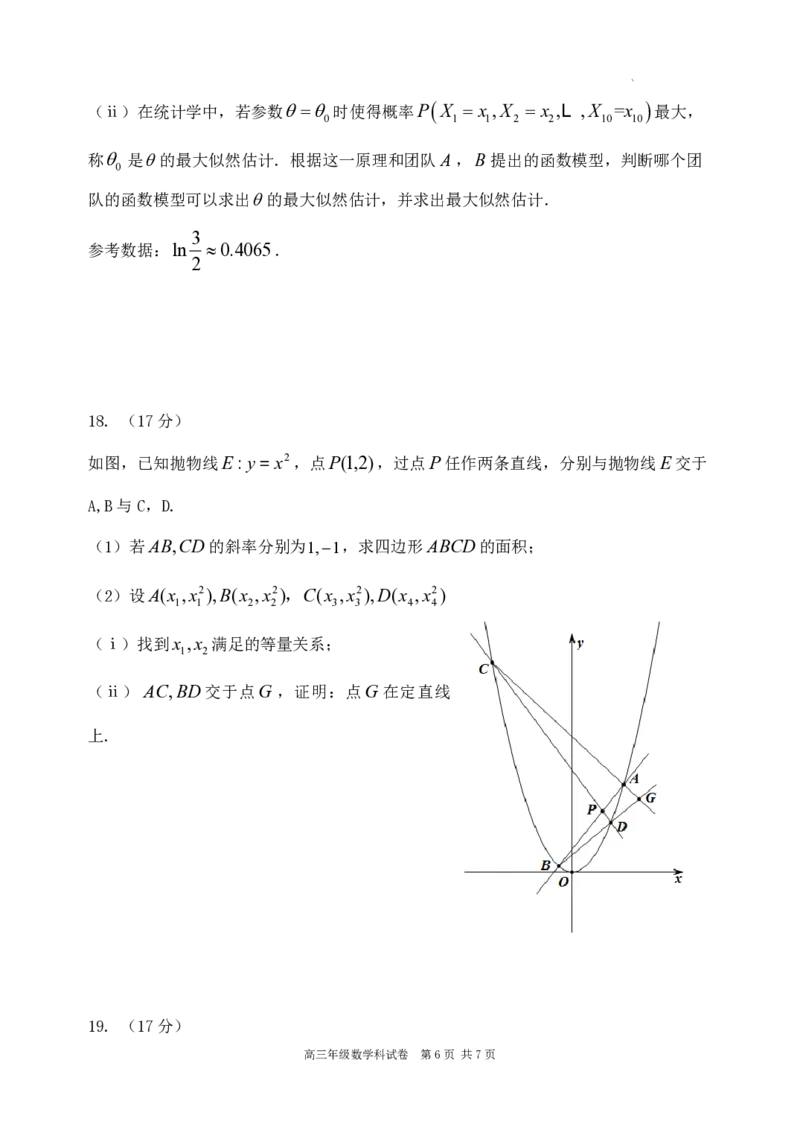（1）若P(X 5) P(X 95)，求数学期望E(X)； （2）接种疫苗后的白鼠被病鼠感染的概率为 p，现有两个不同的研究团队理论研究发 现概率 p与参数(01)的取值有关．团队A提出函数模型为 2 1 p ln(1) 2．团队B提出函数模型为 p   1e ．现将接种疫苗后的白鼠 3 2 分成10组，每组10只，进行实验，随机变量X (i 1,2,L ,10)表示第i组被感染的白 i 鼠数，现将随机变量X (i 1,2,L ,10)的实验结果x (i 1,2,L ,10)绘制成频数分布 i i 图，如图所示． （ⅰ）试写出事件“X  x ，X  x ，…，X  x ”发生的概率表达式（用 p表 1 1 2 2 10 10 示，组合数不必计算）； 高三年级数学科试卷 第5页 共7页 学科网（北京）股份有限公司（ⅱ）在统计学中，若参数 时使得概率PX  x ,X  x ,L ,X =x 最大， 0 1 1 2 2 10 10 称 是的最大似然估计．根据这一原理和团队A，B 提出的函数模型，判断哪个团 0 队的函数模型可以求出的最大似然估计，并求出最大似然估计． 3 参考数据：ln 0.4065． 2 18. （17分） 如图，已知抛物线E: y=x2，点P(1,2)，过点P任作两条直线，分别与抛物线E交于 A,B与C，D. （1）若AB,CD的斜率分别为1,1，求四边形ABCD的面积； （2）设A(x ,x2),B(x ,x2)，C(x ,x2),D(x ,x2) 1 1 2 2 3 3 4 4 （ⅰ）找到x ,x 满足的等量关系； 1 2 （ⅱ） AC,BD交于点G，证明：点G在定直线 上. 19. （17分） 高三年级数学科试卷 第6页 共7页 学科网（北京）股份有限公司已知函数 f(x)lnxax2． （1）讨论函数 f(x)的单调性： （2）若x,x 是方程 f(x)0的两不等实根，求证： 1 2 （i）x2 x2 2e； 1 2 e （ii）x x  ． 1 2 2a 高三年级数学科试卷 第7页 共7页 学科网（北京）股份有限公司