物理答案_6月_240630浙江省台州市2023-2024学年高二下学期6月期末试题

台州市 2023 学年第二学期高二年级期末质量评估试题 物理参考答案及评分标准 2024.06 一、选择题Ⅰ（本题共 13小题，每小题 3分，共 39分。每小题列出的四个备选项中只有一 个是符合题目要求的，不选、多选、错选均不得分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 13 答案 A B C D C B B A B D C B D 二、选择题Ⅱ（本题共 2小题，每小题 3分，共 6分，每小题列出的四个备选项中至少有一 个是符合题目要求的。全部选对的得 3分，选对但不选全的得 2分，有选错的得0分） 题号 14 15 答案 BD AC 三、非选择题（本题共5小题，共 55分） 2 16-Ⅰ.（1）BC （2） （3）0.60 k 16-Ⅱ.（1）AC （2）C （3）2 gL 0 16-Ⅲ.乙 0.6k 增加 17.（1）不变 减小 （2）甲状态时，P  P 4cmHg80cmHg 甲 0 乙状态时，P  P 4cmHg72cmHg 乙 0 根据玻意耳定律PV P V 可知：P L P L 解得：L 30cm 甲 甲 乙 乙 甲 甲 乙 乙 乙 （3）当空气柱长度恢复到27cm时，由盖·吕萨克定律可知： V V 30 27 甲  乙 ，即  解得：T 270K 乙 T T 300K T 甲 乙 乙 mv2 18.（1）小球恰能过C点，则有mg  C R mv2 mv2 小球由B运动到C点过程中，由机械能守恒可知，mg2R C  B 2 2 mv2 小球运动到B点时有，F mg  B ，由此可得，F 6N N R N mv2 （2）若小球恰能过圆轨道最高点，则有mg  h2R  C ，解得h1m 2 若小球恰能运动到圆轨道圆心等高位置，则有mg  hR 0，解得h0.4m 学科网（北京）股份有限公司综上可知，要使小球不脱离竖直圆轨道，则高度h满足0h≤0.4m或h≥1m mv2 （3）①当h1.8m时，小球通过圆轨道到达E点时，速度满足mgh  a ， 2 小球与小物块发生弹性碰撞，射小球碰后速度变为v ，小物块碰后速度为v ， a b mv2 mv2 mv2 则有mv mv mv ， a  a  b a a b 2 2 2 解得v 0，v v 6m/s a b a 当小物块与长木板达到共速时，满足mv  mM  v ，解得v 1m/s b 共 共 ②小物块在长木板上运动过程中，小物块与长木板有两次达到共速，第一次是弹簧被压缩到最短的时候， 第二次是小物块恰好返回到长木板最左端的时候。 方法一、设小物块相对长木板位移位x时，弹簧被压缩到最短，弹性势能大小为E ， P mv2  mM  v2 由能量守恒可知，当二者第一次达共速时， b  E mgx 共 2 P 2 当二者再次达到共速时，E mgx， P mv2  mM  v2 由此可知，2E  b  共 1.5J即E 0.75J P 2 2 P 方法二、对小物块和长木板组成的系统，二者相对滑动过程中因摩擦力做功损失的机械能为 mv2  mM  v2 E  b  共 1.5J 2 2 E 两次共速时系统的总动能相等，由此可知弹簧被压缩到最短时的弹性势能大小为E  0.75J P 2 19.（1）①此时棒ab产生的电动势大小为E  BLv 0 0 E 电路中的电流大小为I  0 解得：I 0.2A 0 R R 0 1 2 ②以水平向右为正方向，由动量定理得BILt 0mv ，q  It 解得：q1C 1 0 （2）①设稳定时棒ab、cd 的速度大小分别为v 和v ，此时电路中的电流为0，即两棒的电动势相等： 1 2 BLv  BLv 1 2 以水平向右为正方向，由动量定理得 棒ab：BILt mv mv 1 1 1 0 学科网（北京）股份有限公司棒cd ：BILt m v 0 2 2 1 解得：v  m/s 2 3 ②方法一：棒ab：W E ，棒cd ：W E 克A1 kab A2 kcd 根据能量守恒定律得：棒ab的动能减少量等于棒ab、cd 的焦耳热与棒cd 的动能增加量之和， E Q E 即W Q W ，所以P  P P kab 总 kcd 克 A1 总 A2 1 R 2 方法二：设此时棒ab、cd 的速度大小分别为v和v BLvBLv 电路中的电流为I  ，P  BILv，P  I2 R R ，P  BILv R R 1 R 1 2 2 1 2 整理得：P  P P 1 R 2 1 2EqL 20.（1）当x2L时， y L，由动能定理得：EqL  mv2解得：v 2 m 进入磁场后，粒子的运动轨迹如图所示，做圆周运动的半径为x2L， mv2 mE 即qvB  解得：B 2L 2qL （2）当x 2L时， y  L，则最后打在y轴上的坐标为 y  y x 3L 1 1 min 1 1 21 当x 3L时，同理可得， y  y x  L 2 max 2 2 4 9 故长度为l  y  y  L max min 4 x2 （3）由（2）同理得，从任意x位置进入电场的粒子打在 y轴上的位置坐标为：y  x 4L  xx 2 从x轴上xx位置进入电场的粒子打在 y轴上的位置坐标为：yy  xx 4L 学科网（北京）股份有限公司2xxx2 2xx xx 两式相减可得：y  x x x 4L 4L 2L n x 1 x2 1 n 0  n ，又 y  x解得：n n y x 0 4L y 0 1 1 2L L  45  （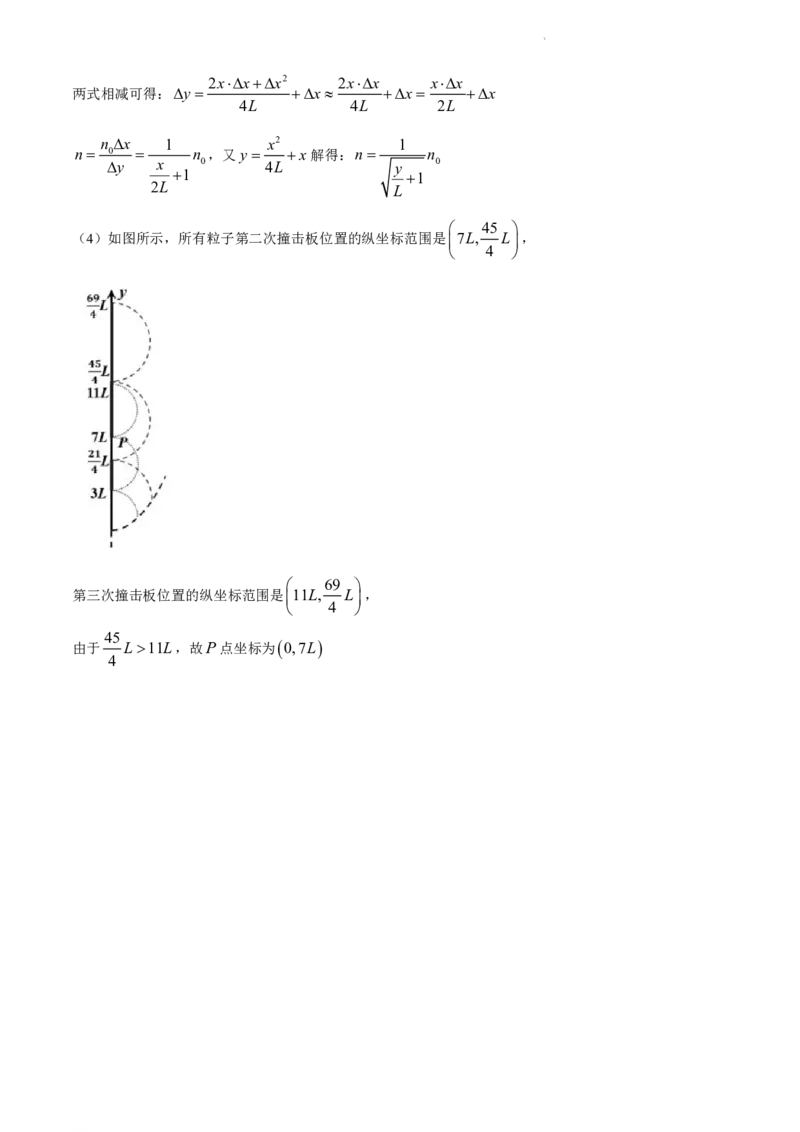4）如图所示，所有粒子第二次撞击板位置的纵坐标范围是7L, L，  4   69  第三次撞击板位置的纵坐标范围是11L, L，  4  45 由于 L11L，故P点坐标为 0,7L  4 学科网（北京）股份有限公司