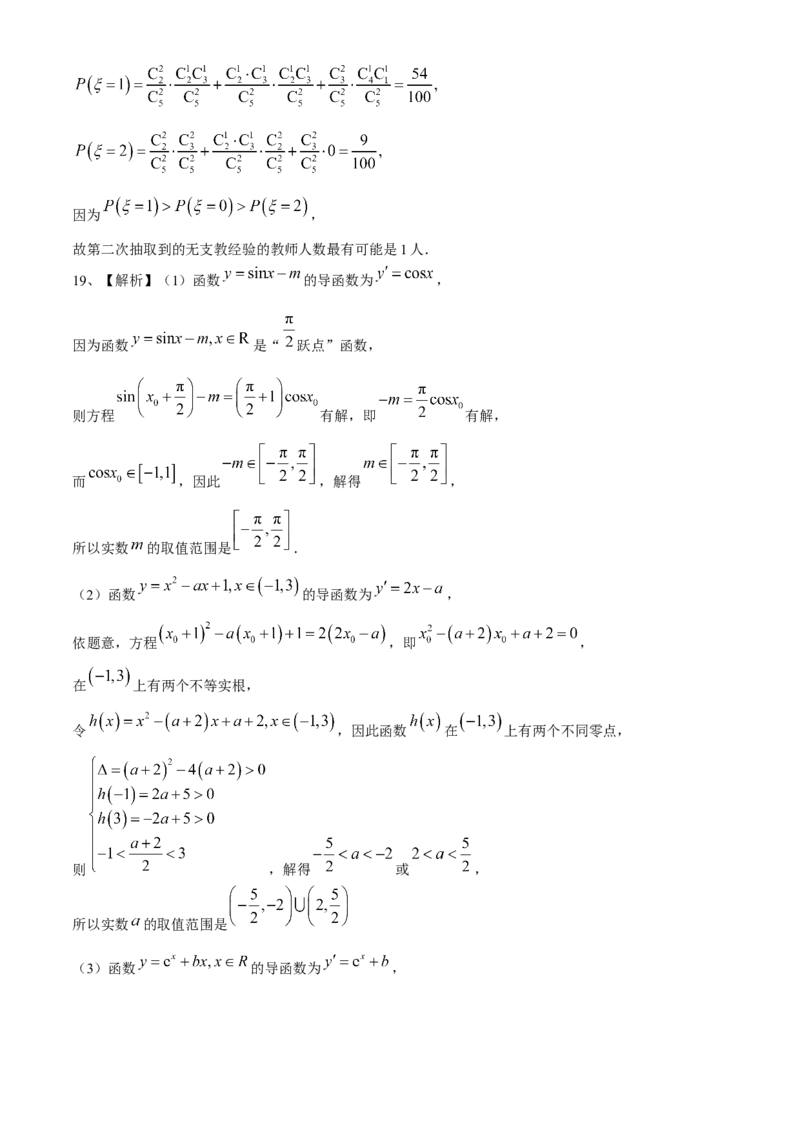文档内容
兰州一中 2023—2024-2 学期 5 月月考试题
高二数学
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分
钟.
2.答卷前,考生务必将自己的姓名、班级填写在答题卡上.
3.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号框涂黑.
如需改动,用橡皮擦干净后,再选涂其它答案标号框.回答非选择题时,将答案写在答题卡
上,写在本试卷上无效.
第Ⅰ卷(选择题)
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.)
1. ,若 共面,则实数 为( )
A.1 B.2 C.3 D.4
2.某学生的 密码是由前两位是大写字母,第三位是小写字母,后六位是数字共九个符号组成.该生
在登录 时,忘记了密码的最后一位数字,如果该生记住密码的最后一位是奇数,则不超过两次就输对
密码的概率为( )
A. B. C. D.
3.水平相当的甲、乙、丙三人举行羽毛球比赛.规则为:每局两人比赛,另一人担任裁判.每局比赛结
束时,负方在下一局比赛中担任裁判.如果第1局甲担任裁判,则第3局甲还担任裁判的概率为( )
A. B. C. D.
4.两平行平面 分别经过坐标原点 和点 ,且两平面的一个法向量 ,则两平面
间的距离是( )
A. B. C. D.
5.袋子中装有5个形状和大小相同的球,其中3个标有字母 个标有字母 .甲先从袋中随机摸一个球,
摸出的球不再放回,然后乙从袋中随机摸一个球,若甲、乙两人摸到标有字母 的球的概率分别为 .
则( )A. B.
C. D.
6.已知事件 互斥,它们都不发生的概率为 ,且 ,则 ( )
A. B. C. D.
7.在四棱锥 中,底面 是边长为3的正方形, 底面 ,点 在侧棱
上.且满足 ,则异面直线 和 的距离为( )
A. B. C. D.
8.托马斯•贝叶斯在研究“逆向概率”的问题中得到了一个公式: ,
这个公式被称为贝叶斯公式(贝叶斯定理),其中 称为 的全概率.春夏换季是流行
性感冒爆发期,已知 三个地区分别有 的人患了流感,且这三个地区的人口数之比是
,现从这三个地区中任意选取1人,若选取的这人患了流感,则这人来自 地区的概率是( )
A.0.25 B.0.27 C.0.48 D.0.52
二、多选题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求,全部选对得6分,部分选对得部分分,有选错的得0分.)
9.对于函数 ,下列说法错误的是( )
A. 有最小值但没有最大值
B.对于任意的 ,恒有
C. 有两个零点
D. 有两个极值点
10.“新高考”后,普通高考考试科目实行“3+1+2”模式,其中“2”就是考生在思想政治、地理、化学、
生物学这4门科目中选择2门作为再选科目.甲、乙两名同学各自从这4门科目中任意挑选2门科目学习.记事件 表示“甲、乙两人中恰有一人选择生物学”,事件 表示“甲、乙两人都选择了生物学”,事件
表示“甲、乙两人所选科目完全相同”,事件 表示“甲、乙两人所选科目不完全相同”,则( )
A. 与 相互独立 B.
C. D.
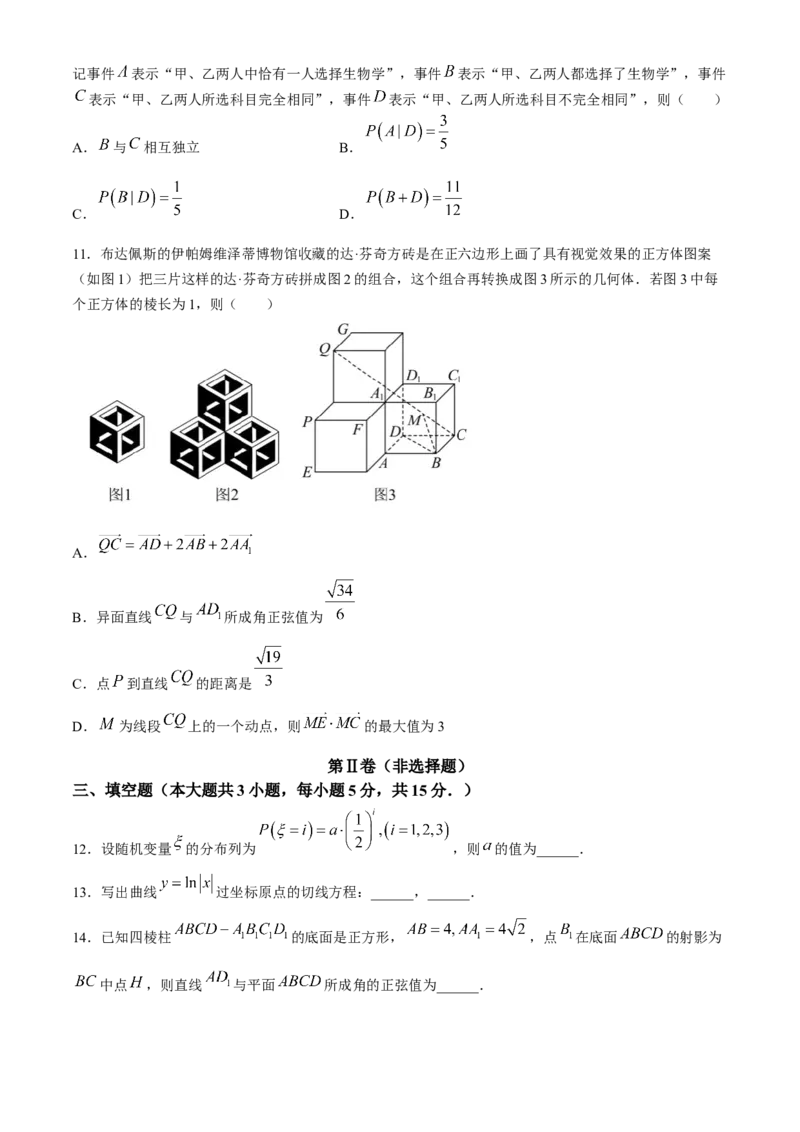
11.布达佩斯的伊帕姆维泽蒂博物馆收藏的达·芬奇方砖是在正六边形上画了具有视觉效果的正方体图案
(如图1)把三片这样的达·芬奇方砖拼成图2的组合,这个组合再转换成图3所示的几何体.若图3中每
个正方体的棱长为1,则( )
A.
B.异面直线 与 所成角正弦值为
C.点 到直线 的距离是
D. 为线段 上的一个动点,则 的最大值为3
第Ⅱ卷(非选择题)
三、填空题(本大题共3小题,每小题5分,共15分.)
12.设随机变量 的分布列为 ,则 的值为______.
13.写出曲线 过坐标原点的切线方程:______,______.
14.已知四棱柱 的底面是正方形, ,点 在底面 的射影为
中点 ,则直线 与平面 所成角的正弦值为______.四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步
骤.)
15.(本题满分13分)
已知口袋中有2个白球和4个红球,现从中随机抽取两次,每次抽取1个.
(1)若采取放回的方法连续抽取两次,求两次都取得白球的概率;
(2)若采取不放回的方法连续抽取两次,求两次至少有一次取得白球的概率;
(3)若采取不放回的方法连续抽取两次,求在第一次取出红球的条件下,第二次取出的是红球的概率
16.(本题满分15分)
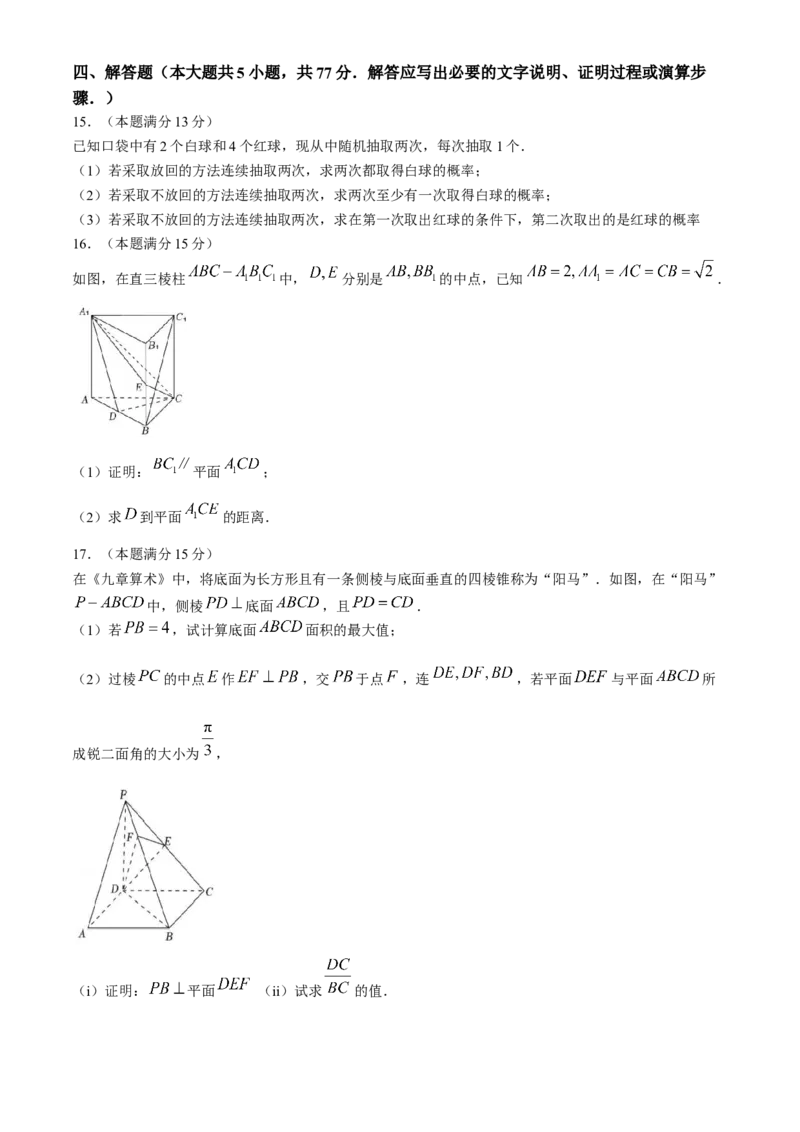
如图,在直三棱柱 中, 分别是 的中点,已知 .
(1)证明: 平面 ;
(2)求 到平面 的距离.
17.(本题满分15分)
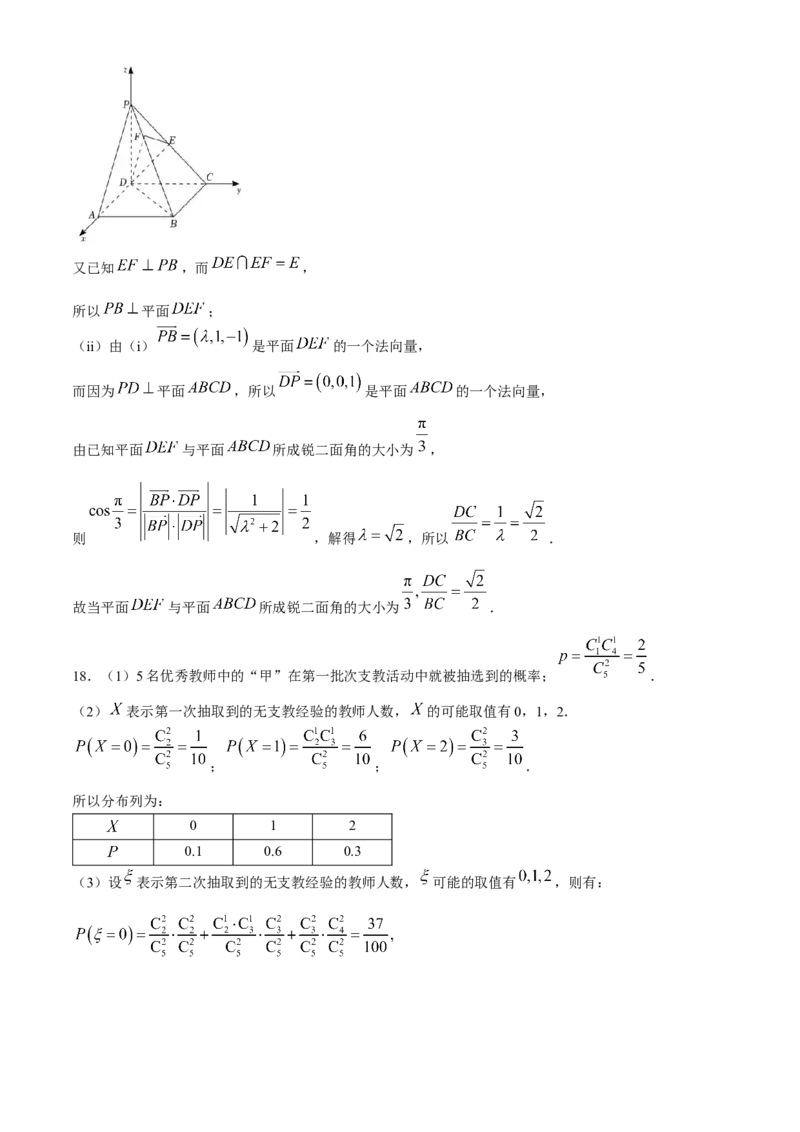
在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称为“阳马”.如图,在“阳马”
中,侧棱 底面 ,且 .
(1)若 ,试计算底面 面积的最大值;
(2)过棱 的中点 作 ,交 于点 ,连 ,若平面 与平面 所
成锐二面角的大小为 ,
(i)证明: 平面 (ii)试求 的值.18.(本题满分17分)
教育是阻断贫困代际传递的根本之策.补齐贫困地区义务教育发展的短板,让贫困家庭子女都能接受公平
而有质量的教育,是夯实脱贫攻坚根基之所在.治贫先治愚,扶贫先扶智.为了解决某贫困地区教师资源
匮乏的问题,某市教育局拟从5名优秀教师中抽选人员分批次参与支教活动.支教活动共分3批次进行,
每次支教需要同时派送2名教师,且每次派送人员均从这5人中随机抽选.已知这5名优秀教师中,2人有
支教经验,3人没有支教经验.
(1)求5名优秀教师中的“甲”,在第一批次支教活动中就被抽选到的概率;
(2)求第一次抽取到无支教经验的教师人数 的分布列;
(3)求第二次抽选时,选到没有支教经验的教师的人数最有可能是几人?请说明理由.
19.(本题满分17分)
对于函数 的导函数 ,若在其定义域内存在实数 和 ,使得
成立,则称 是“跃点”函数,并称 是函数 的“ 跃点”.
(1)若函数 是“ 跃点”函数,求实数 的取值范围;
(2)若函数 是定义在 上的“1跃点”函数,且在定义域内存在两个不同的“1跃
点”,求实数 的取值范围;
(3)若函数 是“1跃点”函数,且在定义域内恰存在一个“1跃点”,求实数 的取
值范围.兰州一中 2023—2024—2 学期 5 月月考试题参考答案
高二数学
一、选择题(本大题共8小题,每小题5分,共40分.)
题号 1 2 3 4 5 6 7 8
答案 D C C B A B A C
二、多选题(本大题共3小题,每小题6分,共18分.全部选对的得6分,部分选对的得部
分分,第10题答对一个选项得2分;第9、11题答对一个选项得3分,有选错的得0分.)
题号 9 10 11
答案 CD BCD BD
三、填空题(本大题共3小题,每小题5分,共15分.)
12. ; 13. ; 14.
四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步
骤.)
15.(1)采取放回的方法,两次都取得白球的概率 ;
(2)采取不放回的方法,两次至少有一次取得白球的概率 ;
(3)记事件 :第一次取出的是红球;事件 :第二次取出的是红球,
则 ,
利用条件概率的计算公式,可得 .
16.(1)证明:连接 交 于点 ,则 为 中点,连接 ,又 是 中点,则 ,平面 平面 ,
平面 ;
(2)如图,以点 为原点,射线 分别为 轴, 轴, 轴的正半轴,
建立空间直角坐标系,
平面 的一个法向量为
D到平面 的距离 .
17.(1)设 ,
由已知可知 ,而底面 的面积为 ,
则由均值不等式,可知 ,
当且仅当 时等号成立;
(2)如图,以点 为原点,射线 分别为 轴, 轴, 轴的正半轴,
建立空间直角坐标系,
(i)设 ,则 ,
所以 ,由于 是 的中点,则 ,故 ,
于是 ,即 ,又已知 ,而 ,
所以 平面 ;
(ii)由(i) 是平面 的一个法向量,
而因为 平面 ,所以 是平面 的一个法向量,
由已知平面 与平面 所成锐二面角的大小为 ,
则 ,解得 ,所以 .
故当平面 与平面 所成锐二面角的大小为 .
18.(1)5名优秀教师中的“甲”在第一批次支教活动中就被抽选到的概率; .
(2) 表示第一次抽取到的无支教经验的教师人数, 的可能取值有0,1,2.
; ; .
所以分布列为:
0 1 2
0.1 0.6 0.3
(3)设 表示第二次抽取到的无支教经验的教师人数, 可能的取值有 ,则有:因为 ,
故第二次抽取到的无支教经验的教师人数最有可能是1人.
19、【解析】(1)函数 的导函数为 ,
因为函数 是“ 跃点”函数,
则方程 有解,即 有解,
而 ,因此 ,解得 ,
所以实数 的取值范围是 .
(2)函数 的导函数为 ,
依题意,方程 ,即 ,
在 上有两个不等实根,
令 ,因此函数 在 上有两个不同零点,
则 ,解得 或 ,
所以实数 的取值范围是
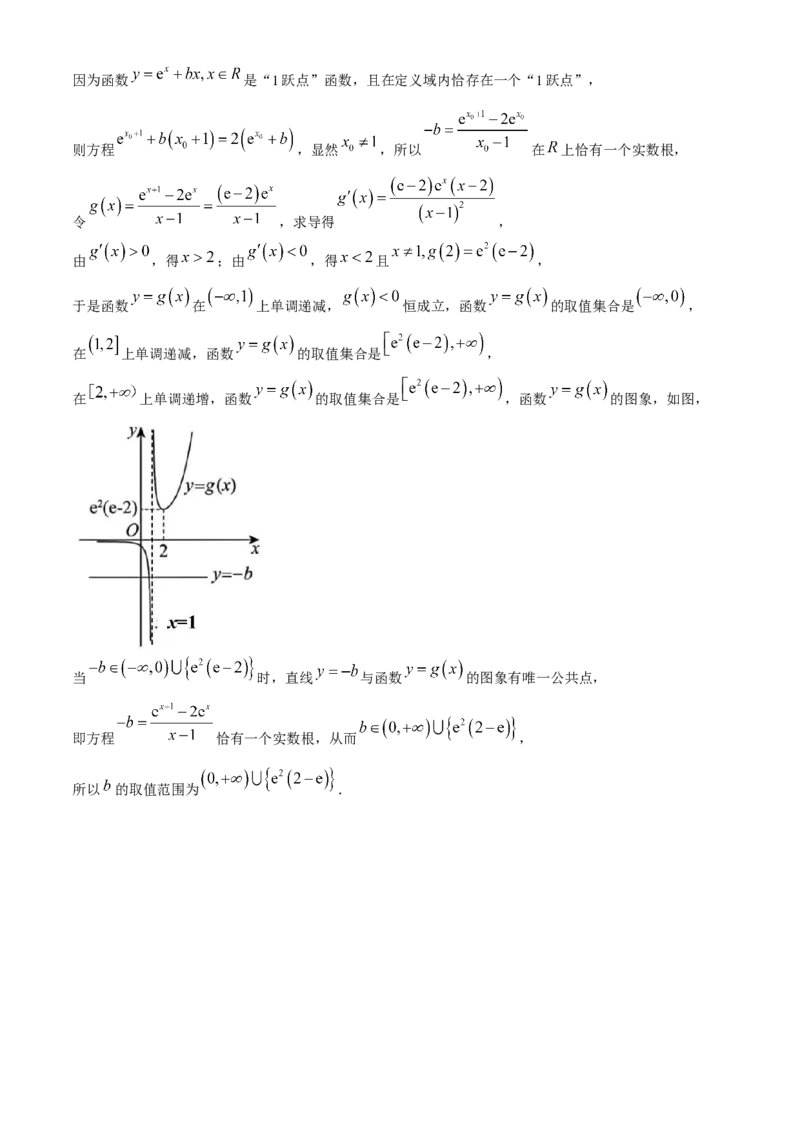
(3)函数 的导函数为 ,因为函数 是“1跃点”函数,且在定义域内恰存在一个“1跃点”,
则方程 ,显然 ,所以 在 上恰有一个实数根,
令 ,求导得 ,
由 ,得 ;由 ,得 且 ,
于是函数 在 上单调递减, 恒成立,函数 的取值集合是 ,
在 上单调递减,函数 的取值集合是 ,
在 上单调递增,函数 的取值集合是 ,函数 的图象,如图,
当 时,直线 与函数 的图象有唯一公共点,
即方程 恰有一个实数根,从而 ,
所以 的取值范围为 .