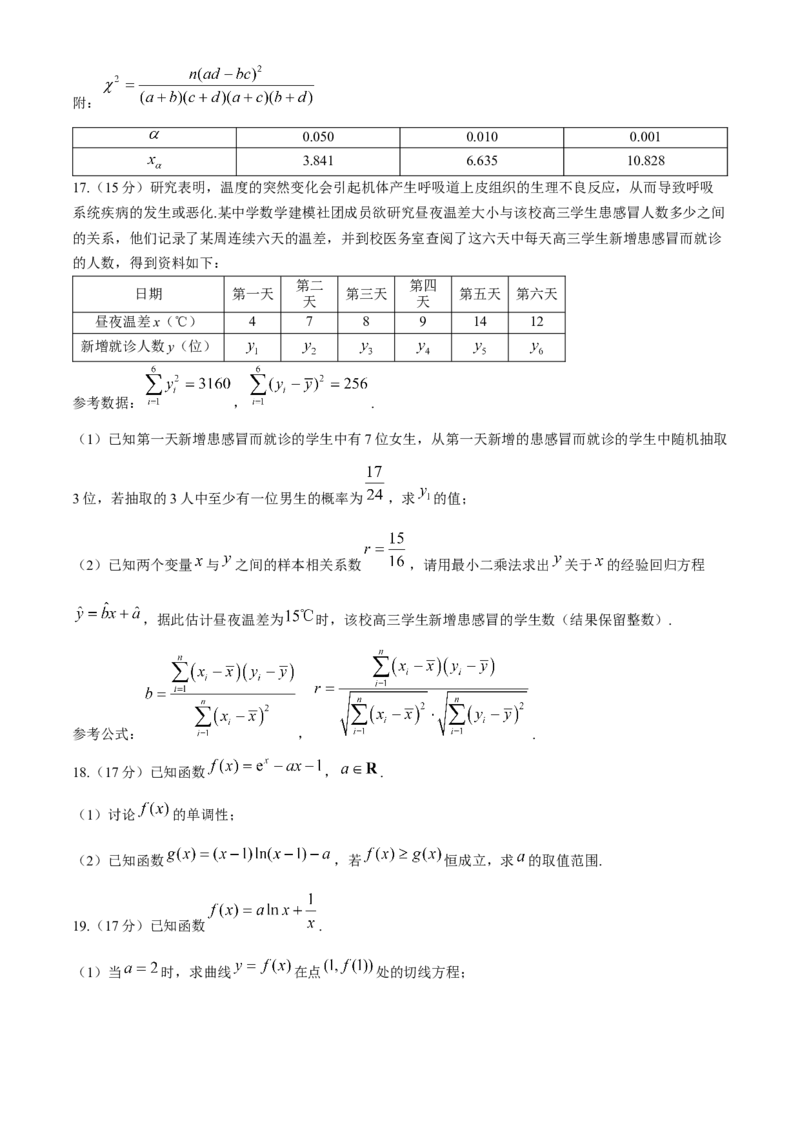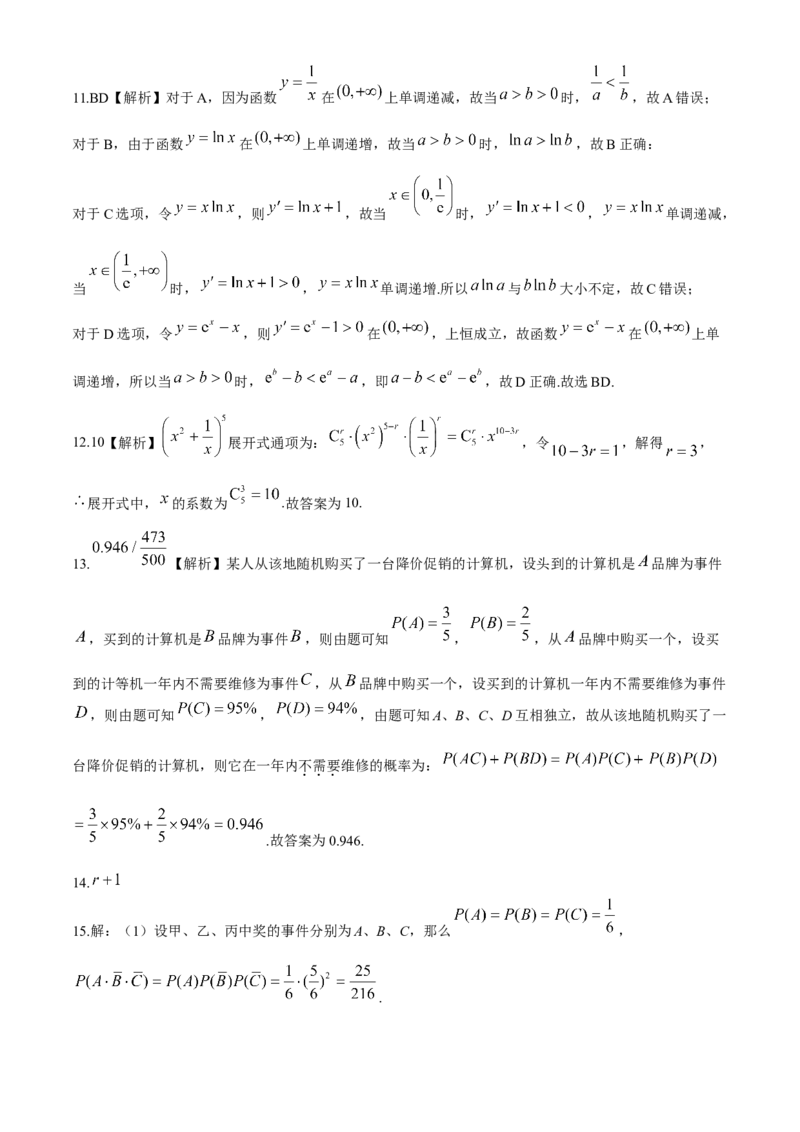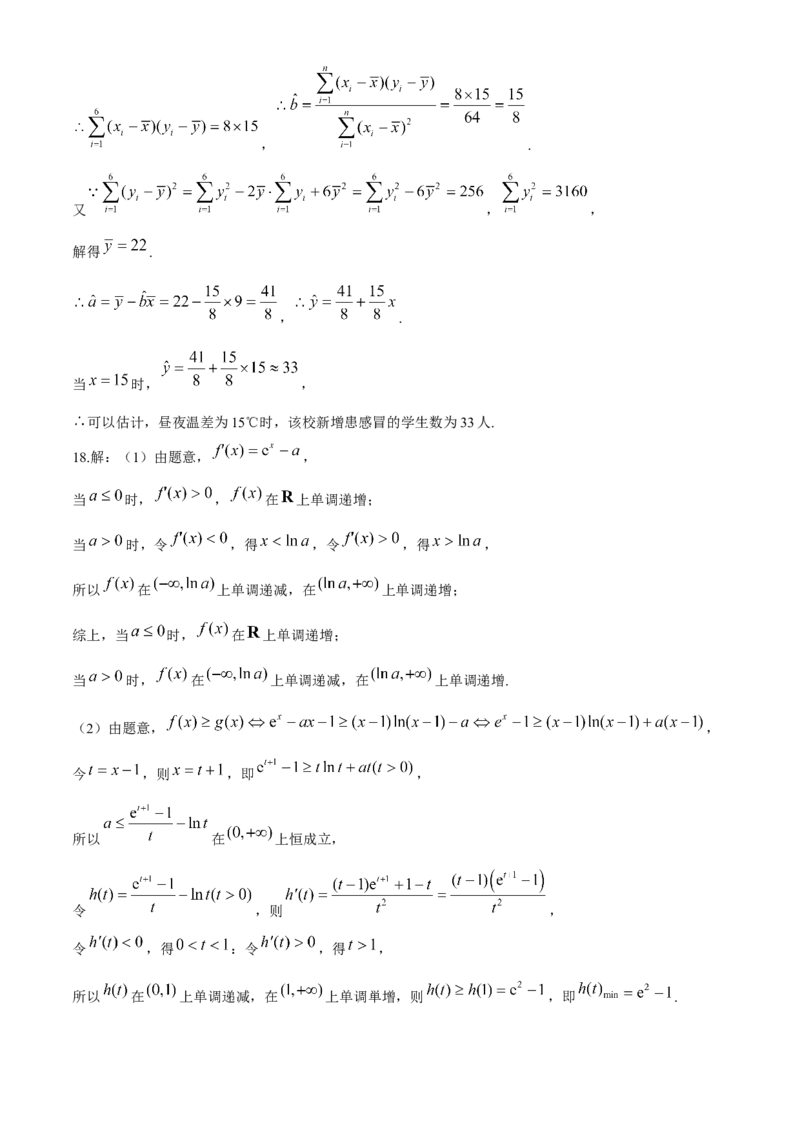文档内容
2023—2024 学年高二期末联考
数学试题
1.答卷前,考生务必将自己的姓名、考场号、座位号、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改
动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在
本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
考试时间为120分钟,满分150分
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项
是符合题目要求的。
1.篮球运动员在比赛中每次罚球得分的规则是:命中得1分,不命中得0分.已知某篮球运动员罚球命中的
概率为0.8,设其罚球一次的得分为X,则( )
A. , B. ,
C. , D. ,
2.函数 的单调递减区间是( )
A. B. C. D.
3.已知有7件产品,其中4件正品,3件次品,每次从中随机取出1件产品,抽出的产品不再放回,那么在
第一次取得次品的条件下,第二次取得正品的概率为( )
A. B. C. D.
4.已知随机变量 服从正态分布 ,且 ,则 ( )
A.0.3 B.0.4 C.0.6 D.0.8
5.有6名男生和5名女生共11名大学生报名参加某社区服务,现从6名男生中选出2名组成一个小组,从5
名女生中选出2名组成一个小组,在周日的上午和下午各安排一个小组值班,则不同的排班种数为( )
A.75 B.150 C.300 D.600
6.已知今天是星期日,则经过 天后是( )
A.星期一 B.星期二 C.星期三 D.星期四
7.一道考题有4个答案,要求学生将其中的一个正确答案选择出来.某考生知道正确答案的概率为 ,在乱
猜时,4个答案都有机会被他选择,若他答对了,则他确实知道正确答案的概率是( )A. B. C. D.
8.已知函数 ,则下面对函数 的描述正确的是( )
A. , B. ,
C. , D.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题
目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.下列说法正确的是( )
A.已知随机变量 ,若 , ,则
B.两位男生和两位女生随机排成一列,则两位女生不相邻的概率是
C.已知 ,则
D.以一批含有10件正品、4件次品的产品中任取3件,则取得2件次品的概率为
10.若 ,则( )
A. B.
C. D.
11.若a,b为正实数,且 ,则下列不等式成立的是( )
A. B.
C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.在 的展开式中,x的系数为________.
13.已知某地只有A,B两个品牌的计算机在进行降价促销活动,售后保修期为1年,它们在市场的占有率
之比为3:2.根据以往数据统计,这两个品牌的计算机在使用一年内,A品牌有5%需要维修,B品牌有6%需要维修.若某人从该地随机购买了一台降价促销的计算机,则它在一年内不需要维修的概率为________.
________.
14.将杨辉三角中的每一个数 都换成分数 ,可得到如图所示的分数三角形,成为“莱布尼茨三
角形”,从莱布尼茨三角形可以看出,存在x使得 ,则x的值是_________.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内
印有“奖励一瓶”字样即为中奖,中奖概率为 .甲、乙、丙三位同学每人购买了一瓶该饮料。
(1)求甲中奖且乙、丙都没有中奖的概率;
(2)求中奖人数 的分布列及数学期望 .
16.(15分)某数学兴趣小组为研究本校学生数学成绩与语文成绩的关系,采取有放回的简单随机抽样,
从学校抽取样本容量为200的样本,将所得数学成绩与语文成绩的样本观测数据整理如下:
语文成绩
合计
优秀 不优秀
优秀 50 30 80
数学成绩 不优 40 80 120
秀
合计 90 110 200
(1)根据 的独立性检验,能否认为数学成绩与语文成绩有关联?
(2)在人工智能中常用 表示在事件A发生的条件下事件B发生的优势,在统计中称
为似然比,现从该校学生中任选一人,A表示“选到的学生语文成绩不优秀”,B表示“选到的学生数学
成绩不优秀”请利用样本数据,估计 的值.附:
0.050 0.010 0.001
3.841 6.635 10.828
17.(15分)研究表明,温度的突然变化会引起机体产生呼吸道上皮组织的生理不良反应,从而导致呼吸
系统疾病的发生或恶化.某中学数学建模社团成员欲研究昼夜温差大小与该校高三学生患感冒人数多少之间
的关系,他们记录了某周连续六天的温差,并到校医务室查阅了这六天中每天高三学生新增患感冒而就诊
的人数,得到资料如下:
第二 第四
日期 第一天 第三天 第五天 第六天
天 天
昼夜温差x(℃) 4 7 8 9 14 12
新增就诊人数y(位)
参考数据: , .
(1)已知第一天新增患感冒而就诊的学生中有7位女生,从第一天新增的患感冒而就诊的学生中随机抽取
3位,若抽取的3人中至少有一位男生的概率为 ,求 的值;
(2)已知两个变量 与 之间的样本相关系数 ,请用最小二乘法求出 关于 的经验回归方程
,据此估计昼夜温差为 时,该校高三学生新增患感冒的学生数(结果保留整数).
参考公式: , .
18.(17分)已知函数 , .
(1)讨论 的单调性;
(2)已知函数 ,若 恒成立,求 的取值范围.
19.(17分)已知函数 .
(1)当 时,求曲线 在点 处的切线方程;(2)当 时,求函数 的零点个数;
(3)若对任意的 ,都有 ,求实数 的最大值.2023-2024学年高二期末联考
数学参考答案及评分意见
1.D【解析】由题意, 服从两点分布,所以 , .故选D.
2.C【解析】 ,令 ,解得 ,所以函数 在区间 上单调
递增.故选C.
3.B【解析】设事件A表示“第一次取的次品”,事件B表示“第二次取得正品”,则 ,
, ,故选B.
4.A【解析】由题意,随机变量服从正态分布 ,所以 ,即图象的对称轴为 ,又由
,则 ,则 ,所以
,故选A.
5.C【解析】由题意,其有 (种),故选C.
6.C【解析】
.
由于 能被7整除.
故 除以7余3,今天是星期日,则 天后是星期三.故选C.
7.B【解析】设事件 表示“考生答对”.事件 表示“考生知道正确䈶案”,由全概率公式得
.
学科网(北京)股份有限公司又由贝叶斯公式得 .故选B.
8.B【解析】将 代入 ,得 ,故排除A,D,又因为 .所
以 ,导函数 在 上是增函数.又 ,
,所以 在 上有唯一的实根,设为 ,且 ,则
为 的最小值点,且 ,即 .故
,又 , ,
,即对 , .故选B.
9.BC
10.BCD【解析】对于A,令 ,则 ;令 ,则 ,所以
,故A错误;对于B,令 ,则 ,
又 ,以上两式相加可得 ,所以 ,
所以 ,故B正确;对于C,因为
,所以选4个 ,1个1或者
选2个 ,3个 即可求出展开式中 的系数为 ,则 ,故C正确;对
于D,因为 是 的展开式的系数和,所以令 ,则
,故D正确.故选BCD.
学科网(北京)股份有限公司11.BD【解析】对于A,因为函数 在 上单调递减,故当 时, ,故A错误;
对于B,由于函数 在 上单调递增,故当 时, ,故B正确:
对于C选项,令 ,则 ,故当 时, , 单调递减,
当 时, , 单调递增.所以 与 大小不定,故C错误;
对于D选项,令 ,则 在 ,上恒成立,故函数 在 上单
调递增,所以当 时, ,即 ,故D正确.故选BD.
12.10【解析】 展开式通项为: ,令 ,解得 ,
展开式中, 的系数为 .故答案为10.
13. 【解析】某人从该地随机购买了一台降价促销的计算机,设头到的计算机是 品牌为事件
,买到的计算机是 品牌为事件 ,则由题可知 , ,从 品牌中购买一个,设买
到的计等机一年内不需要维修为事件 ,从 品牌中购买一个,设买到的计算机一年内不需要维修为事件
,则由题可知 , ,由题可知A、B、C、D互相独立,故从该地随机购买了一
台降价促销的计算机,则它在一年内不需要维修的概率为:
.故答案为0.946.
14.
15.解:(1)设甲、乙、丙中奖的事件分别为A、B、C,那么 ,
.
学科网(北京)股份有限公司(2) 的可能值为 ,
所以中奖人数 的分布列为
0 1 2 3
P
故 ,故数学期望 为 .
16.解:(1)零假设 :数学成绩与语文成绩无关联.
据表中数据计筫得
根据小概率值 的 的独立性检验,我们推断 不成立,故认为数学成绩与语文成绩有关联;
(2) .
估计 的值为 .
17.解:(1) , ,
又 , ,
(2) , ,
.
,
学科网(北京)股份有限公司, .
又 , ,
解得 .
, .
当 时, ,
可以估计,昼夜温差为15℃时,该校新增患感冒的学生数为33人.
18.解:(1)由题意, ,
当 时, , 在 上单调递增;
当 时,令 ,得 ,令 ,得 ,
所以 在 上单调递减,在 上单调递增;
综上,当 时, 在 上单调递增;
当 时, 在 上单调递减,在 上单调递增.
(2)由题意, ,
今 ,则 ,即 ,
所以 在 上恒成立,
令 ,则 ,
令 ,得 :令 ,得 ,
所以 在 上单调递减,在 上单调単增,则 ,即 .
学科网(北京)股份有限公司,此时, 在 上恒成立,即 恒成立.
故实数 的取值范围为 .
19.解:(1)当 时,函数 ,可得 ,
所以 且 ,即切线的斜率为 且切点坐标为 ,
所以切线方程为 ,即 .
(2)当 时,函数 ,可得 , ,
当 时, , 单调递减;
当 时, , 单调递增,
所以当 时,函数 取得极小值,也为最小值 ,
所以 ,所以函数 没有零点,即函数 的零点个数为0.
(3)由对任意的 ,都有 成立,即 成立,
令 , ,可得 ,
因为 ,要使得 恒成立,则满足 ,即 ,故 .
下面证明:当 时,符合题意,
此时 , ,令 , ,
可得 ,所以 为单调递减函数,
学科网(北京)股份有限公司因为 ,所以 ,即 ,
所以 恒成立,
即当 时,对任意的 ,都有 成立,即 .
综上可得,实数a的最大值为2.
学科网(北京)股份有限公司