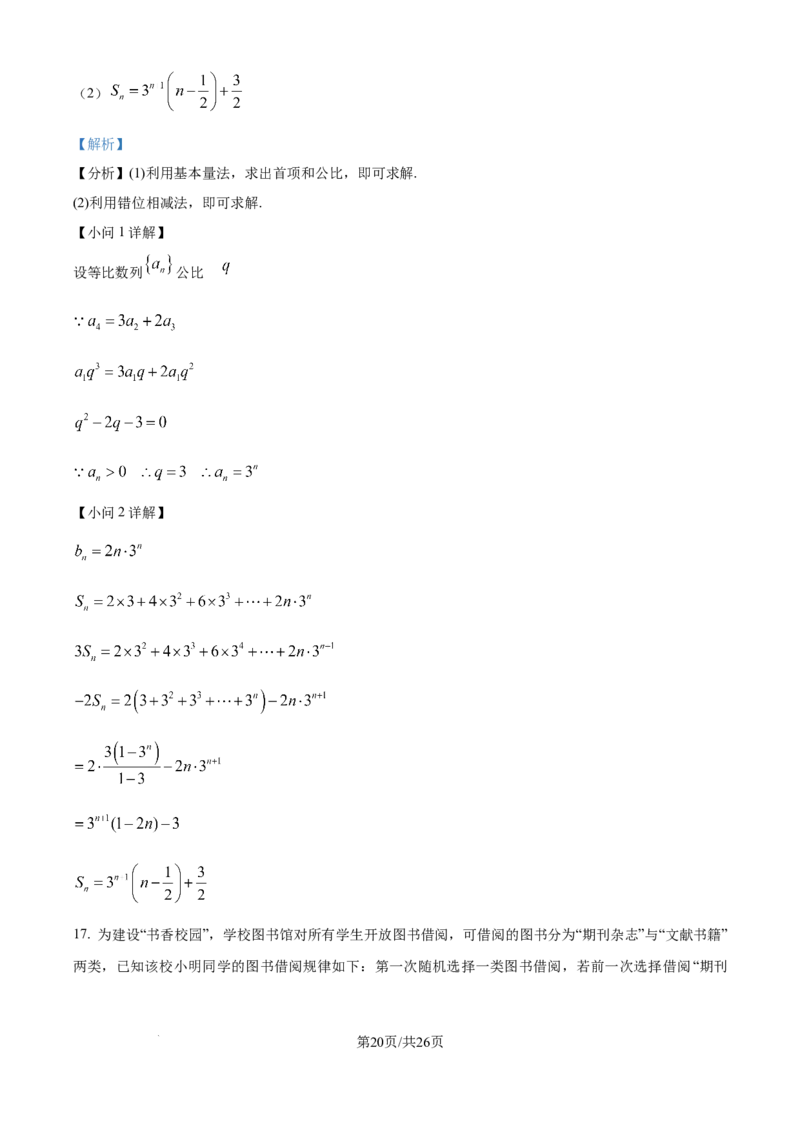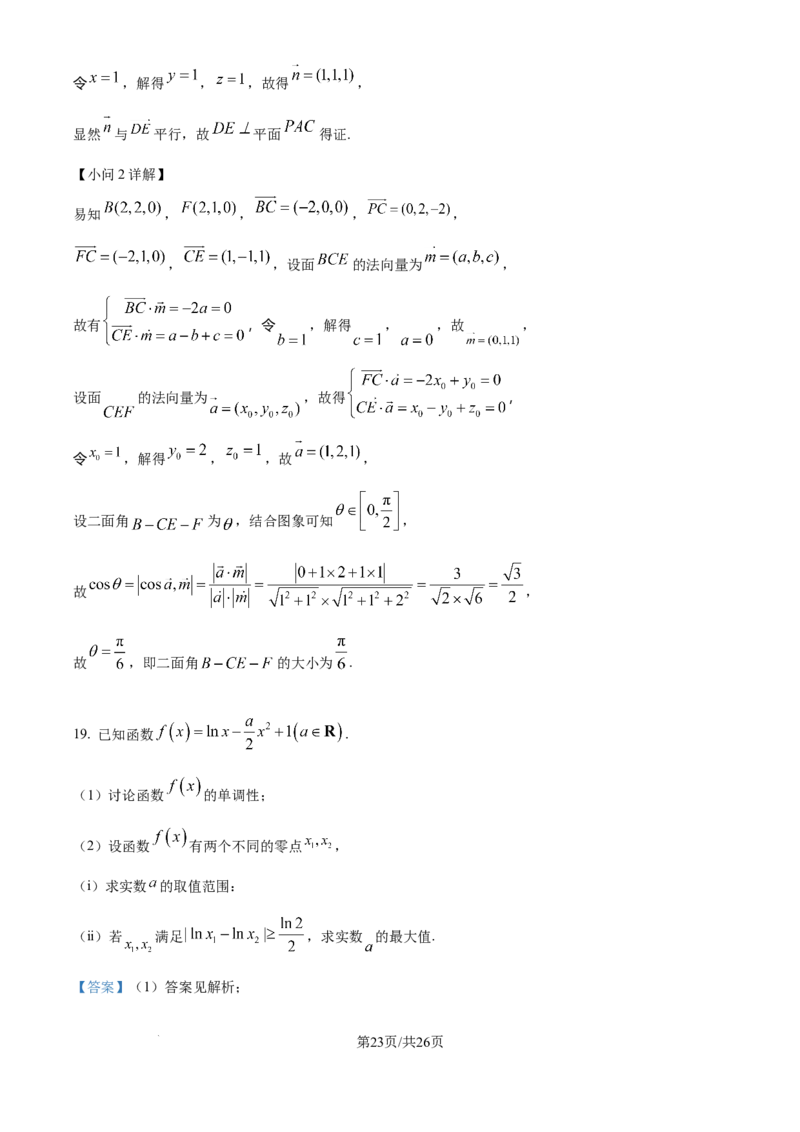文档内容
衡阳市一中 2022 级 2023-2024 学年下学期期末考试
高二数学
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 函数 在 上的单调性是( ).
A. 单调递增
B. 单调递减
C. 在 上单调递减,在 上单调递增
D. 在 上单调递增,在 上单调递减
【答案】C
【解析】
【分析】利用导数判断函数 在 上的单调性.
【详解】 ,令 ,得 ;
令 ,得 ,
∴函数 在 上单调递减,在 上单调递增.
故选:C
第1页/共26页
学科网(北京)股份有限公司2. 已知数列 是由正数组成的等比数列, 为其前 项和.已知 ,则 ( )
A. 15 B. 17 C. 31 D. 33
【答案】C
【解析】
【分析】先判断 ,再求出首项和公比,注意各项均为正数,再求 即可.
【详解】解:设公比为 ,显然 ,
则 ,所以 ,
所以 ,
故选:C
【点睛】考查等比数列的有关计算,基础题.
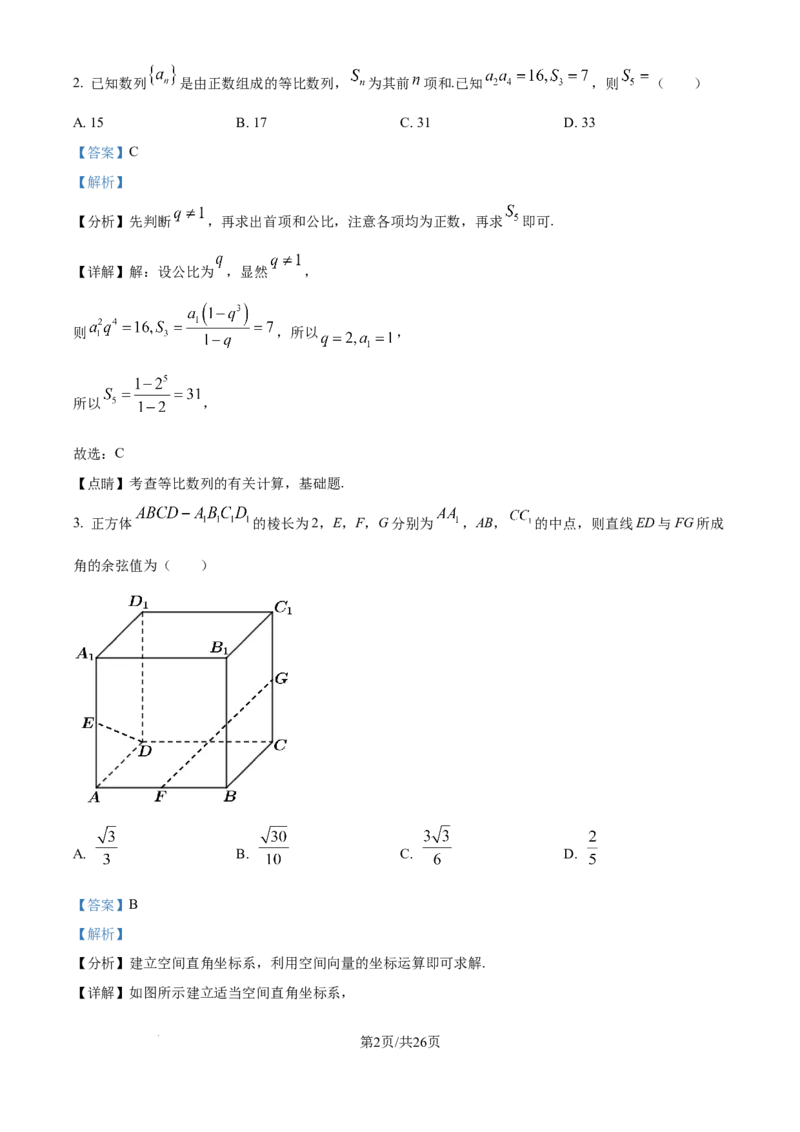
3. 正方体 的棱长为2,E,F,G分别为 ,AB, 的中点,则直线ED与FG所成
角的余弦值为( )
A. B. C. D.
【答案】B
【解析】
【分析】建立空间直角坐标系,利用空间向量的坐标运算即可求解.
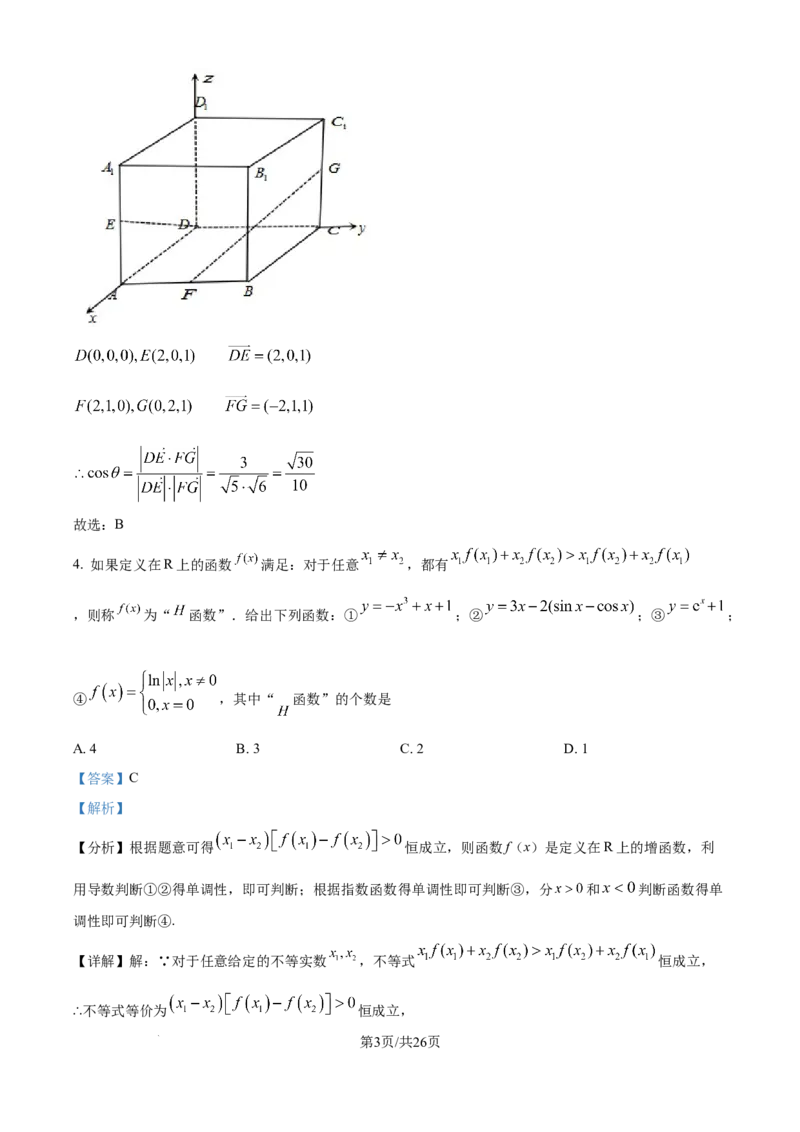
【详解】如图所示建立适当空间直角坐标系,
第2页/共26页
学科网(北京)股份有限公司故选:B
4. 如果定义在R上的函数 满足:对于任意 ,都有
,则称 为“ 函数”.给出下列函数:① ;② ;③ ;
④ ,其中“ 函数”的个数是
A. 4 B. 3 C. 2 D. 1
【答案】C
【解析】
【分析】根据题意可得 恒成立,则函数f(x)是定义在R上的增函数,利
用导数判断①②得单调性,即可判断;根据指数函数得单调性即可判断③,分 和 判断函数得单
调性即可判断④.
【详解】解:∵对于任意给定的不等实数 ,不等式 恒成立,
∴不等式等价为 恒成立,
第3页/共26页
学科网(北京)股份有限公司即函数f(x)是定义在R上的增函数,
① , ,当 或 时, ,
所以函数 在 和 上递减,故不满足条件;
② ; ,
所以函数单调递增,满足条件;
③ 为增函数,满足条件;
④ ,当x>0时,函数单调递增,当x<0时,函数单调递减,不满足条件,
综上满足“H函数”的函数为②③.
故选:C.
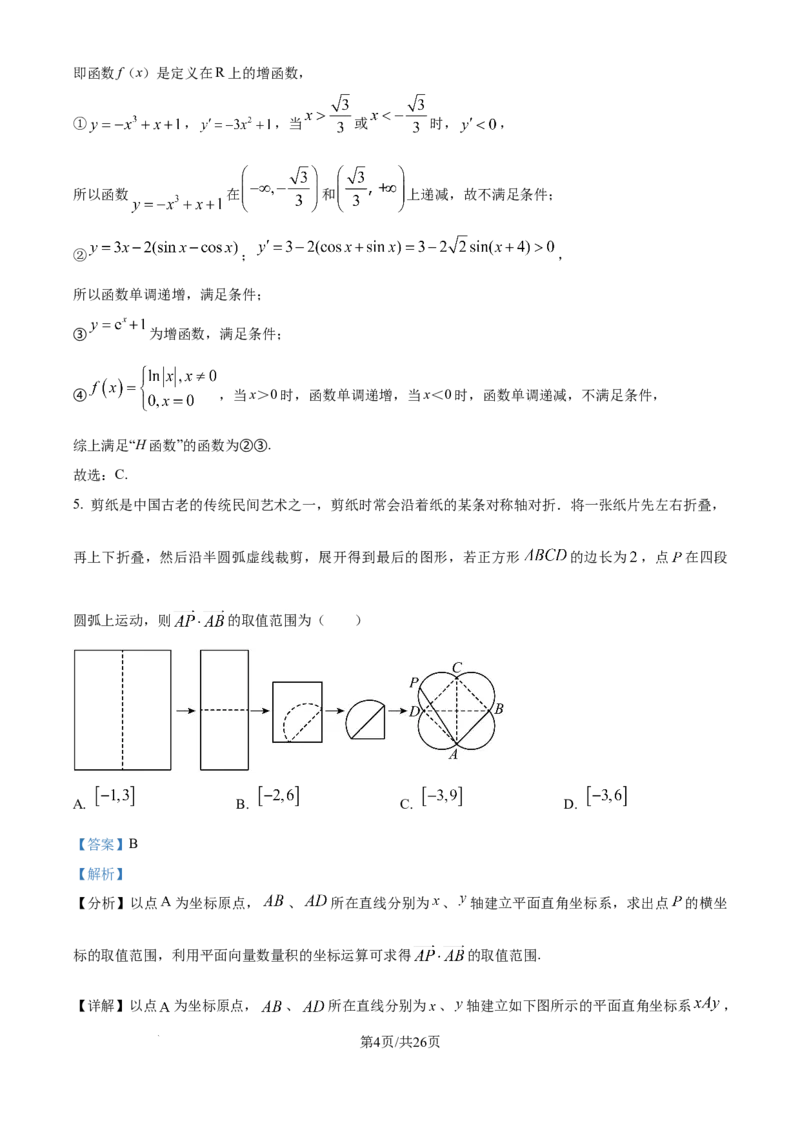
5. 剪纸是中国古老的传统民间艺术之一,剪纸时常会沿着纸的某条对称轴对折.将一张纸片先左右折叠,
再上下折叠,然后沿半圆弧虚线裁剪,展开得到最后的图形,若正方形 的边长为 ,点 在四段
圆弧上运动,则 的取值范围为( )
A. B. C. D.
【答案】B
【解析】
【分析】以点 为坐标原点, 、 所在直线分别为 、 轴建立平面直角坐标系,求出点 的横坐
标的取值范围,利用平面向量数量积的坐标运算可求得 的取值范围.
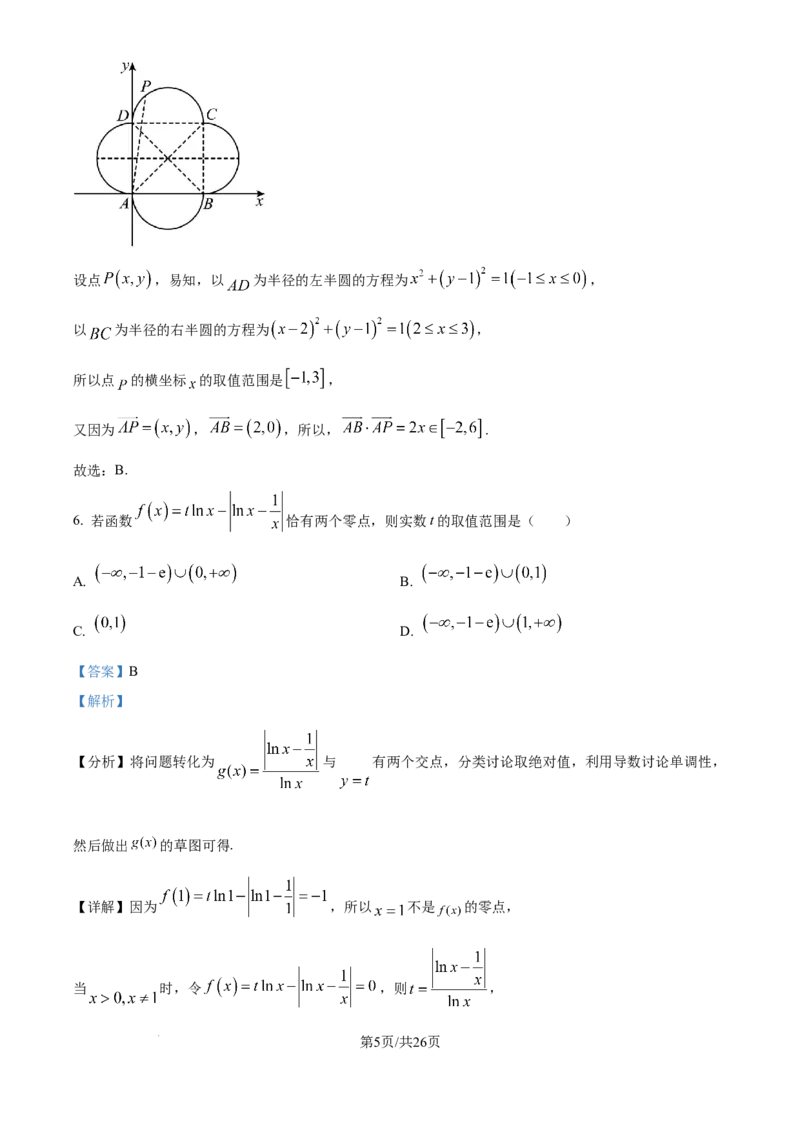
【详解】以点 为坐标原点, 、 所在直线分别为 、 轴建立如下图所示的平面直角坐标系 ,
第4页/共26页
学科网(北京)股份有限公司设点 ,易知,以 为半径的左半圆的方程为 ,
以 为半径的右半圆的方程为 ,
所以点 的横坐标 的取值范围是 ,
又因为 , ,所以, .
故选:B.
6. 若函数 恰有两个零点,则实数t的取值范围是( )
A. B.
C. D.
【答案】B
【解析】
【分析】将问题转化为 与 有两个交点,分类讨论取绝对值,利用导数讨论单调性,
然后做出 的草图可得.
【详解】因为 ,所以 不是 的零点,
当 时,令 ,则 ,
第5页/共26页
学科网(北京)股份有限公司记 ,
则问题转化为 与 有两个交点,
易知 在 上单调递增,
又 ,
所以 的零点 ,当 时 ,当 时 ,
当 且 时, ,
令 ,得
当 时, , 单调递增,当 或 时, , 单调递减,
当 时, ,则 , 单调递增,
且当x趋近于0或从左趋近于1时, 趋近于 ,当x从右趋近于1时, 趋近于 ,当x趋近于
时, 趋近于1.
又 ,
所以可作 的草图如下:
第6页/共26页
学科网(北京)股份有限公司由图可知,当 或 时, 与 有两个交点,即 有两个零点.
故选:B
7. 已知点 ,若圆 上存在点 ,使得线段 的中点也在圆 上,则 的取值范围是
( )
A. B. C. D.
【答案】B
【解析】
【分析】
根据已知用相关点法,求出 中点 的轨迹方程,又有 点在圆上,可得 点轨迹与圆有公共点,求
出 的范围.
【详解】设 , 的中点 ,
由已知有 解得 ,
即 的中点的轨迹为圆 ,
又线段 的中点也在圆 上,∴两圆有公共点,
第7页/共26页
学科网(北京)股份有限公司∴ ,解得 .
故选:B.
【点睛】本题考查动点轨迹方程的求法,以及圆与圆的位置关系,属于中档题.
8. 若 , , ,则( )
.
A B.
C. D.
【答案】B
【解析】
【分析】利用对数运算结合对数函数单调性可得 ,并与 比较大小,再构造函数
,可得 ,即可与c比较大小作答.
【详解】依题意, ,
令函数 ,求导得
,
函数 在 上单调递减, ,即当 时,
,
,
第8页/共26页
学科网(北京)股份有限公司,即 ,因此 ,
所以 .
故选:B
【点睛】思路点睛:某些数或式大小关系问题,看似与函数的单调性无关,细心挖掘问题的内在联系,抓
住其本质,构造函数,分析并运用函数的单调性解题,它能起到化难为易、化繁为简的作用.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知平行六面体 如图所示,其中 , ,
,线段AC,BD交于点O,点E是线段 上靠近 的三等分点,则下列说法正确的是(
)
A. B.
C. D.
【答案】AD
【解析】
【分析】由向量的线性运算和数量积的定义,化简求值.
【详解】依题意, ,
, ,
第9页/共26页
学科网(北京)股份有限公司,故A正确;
,故B错误;
,
则 ,故C错误;
,故D正确;
故选:AD.
10. 设函数 ,且 ,下列命题:其中正确的命题是( )
.
A 若 ,则 ;
B. 存在 , ,使得 ;
C. 若 , ,则 ;
D. 对任意的 , ,都有 .
【答案】BCD
【解析】
第10页/共26页
学科网(北京)股份有限公司【分析】
结合割线与切线斜率的大小关系即可判断选项A、B、C,根据中位线与函数值的大小比较可判断选项D,
进而可得正确选项.
【详解】
由 可得 ,
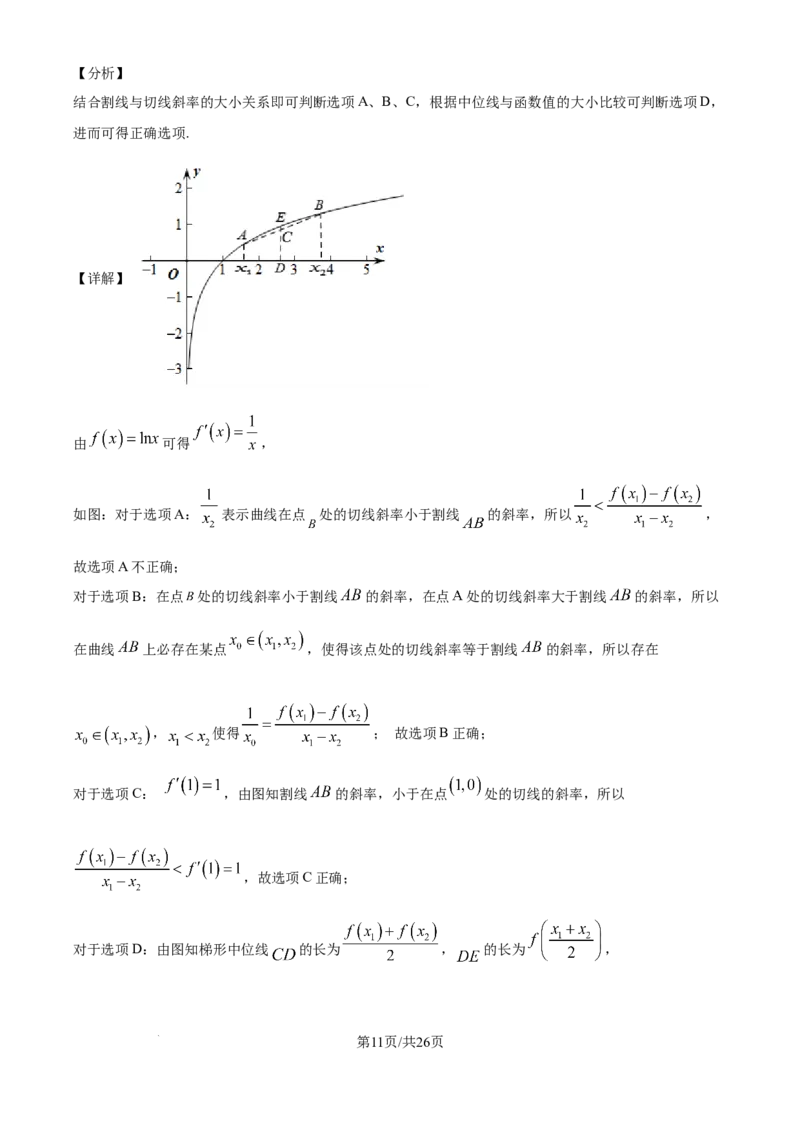
如图:对于选项A: 表示曲线在点 处的切线斜率小于割线 的斜率,所以 ,
故选项A不正确;
对于选项B:在点 处的切线斜率小于割线 的斜率,在点 处的切线斜率大于割线 的斜率,所以
在曲线 上必存在某点 ,使得该点处的切线斜率等于割线 的斜率,所以存在
, 使得 ; 故选项B正确;
对于选项C: ,由图知割线 的斜率,小于在点 处的切线的斜率,所以
,故选项C正确;
对于选项D:由图知梯形中位线 的长为 , 的长为 ,
第11页/共26页
学科网(北京)股份有限公司因为 ,所以 ,故选项D正确;
故选:BCD公众号:高中试卷君
【点睛】关键点点睛:本题解题的关键点是利用导数的几何意义,数形结合比较切线和割线的斜率,理解
凸函数的性质.
11. 已知函数 ,则下列结论正确的是( )
A. 函数 存在三个不同的零点
B. 函数 的极小值为 ,极大值为
C. 若 时, ,则t的最大值为2
D. 若方程 有两个实根,则
【答案】BCD
【解析】
【分析】解方程求出零点判断A;利用导数求出函数 的极值判断B;求出函数单调区间,数形结合判
断CD.
【详解】对于A,由 ,得 ,解得 ,函数 只有两个零点,A错误;
对于B,函数 定义域为R,求导得 ,
当 或 时, ,当 时, ,
函数 的极小值为 ,极大值为 ,B正确;
对于C,函数 在 上单调递减,在 上单调递增,
第12页/共26页
学科网(北京)股份有限公司当 时, 单调递减,值域为 ,而 ,
则 ,函数 在 上的值域为 ,
当 时, 恒成立,函数 在 上的值域为 ,
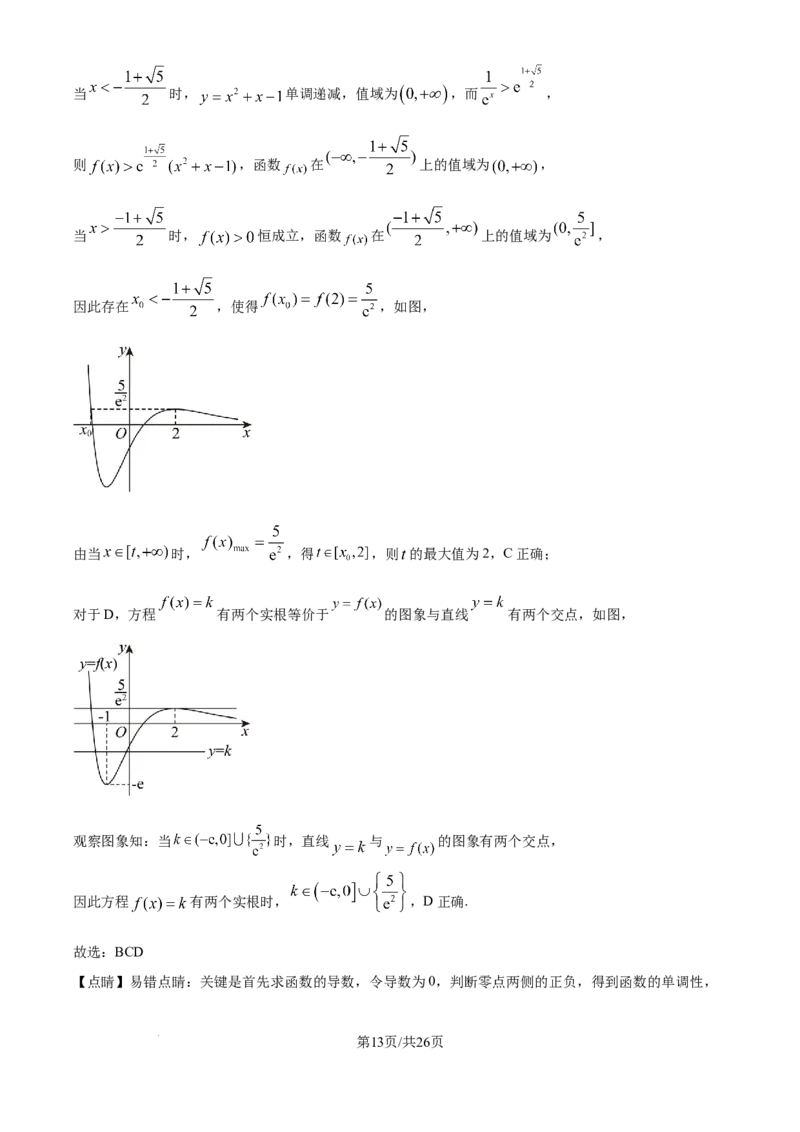
因此存在 ,使得 ,如图,
由当 时, ,得 ,则 的最大值为2,C正确;
对于D,方程 有两个实根等价于 的图象与直线 有两个交点,如图,
观察图象知:当 时,直线 与 的图象有两个交点,
因此方程 有两个实根时, ,D正确.
故选:BCD
【点睛】易错点睛:关键是首先求函数的导数,令导数为0,判断零点两侧的正负,得到函数的单调性,
第13页/共26页
学科网(北京)股份有限公司要注意 是函数的单调递减区间,且 恒成立,图象是无限接近 轴,如果这里判断错了,
那选项就容易判断错了.
三、填空题:本题共3小题,每小题5分,共15分
12. “中国剩余定理”又称“孙子定理”.“中国剩余定理”讲的是关于带余除法的问题,现有这样一个问题:将
2至2019这2018个整数中被5除余1且被7除余1的数按由小到大的顺序排成一列,构成数列 ,则此
数列的项数为_______.
【答案】57
【解析】
【分析】由题意可得 ,令 ,求出n的最大值即可得解.
【详解】被5除余1且被7除余1的数就是被35除余1的数,故 .
由 可得 可取的最大整数为57,故此数列最后一项的项数为57.
故答案为:57.
【点睛】本题考查了数列通项公式的应用,属于基础题.
13. 已知 为坐标原点,抛物线 的焦点为 ,过 的直线交 于A,B两点,A,B
中点 在 轴上方且其横坐标为1, ,则直线 的斜率为______.
【答案】
【解析】
【分析】设出直线 的方程为: ,将直线方程与抛物线方程联立,利用韦达定理和
弦长公式,以及中点坐标即可求解.
【详解】由题意可知:直线 的斜率存在且大于零,
则设直线 的方程为: , ,
第14页/共26页
学科网(北京)股份有限公司联立方程组 ,整理可得: ,
则 , ,又因为A,B中点 的横坐标为1,
所以 ,则 ,
由弦长公式可得: ,
又因为 ,则有 ,
化简整理可得: ,即 ,解得: ,
因为 ,所以 ,
故答案为: .
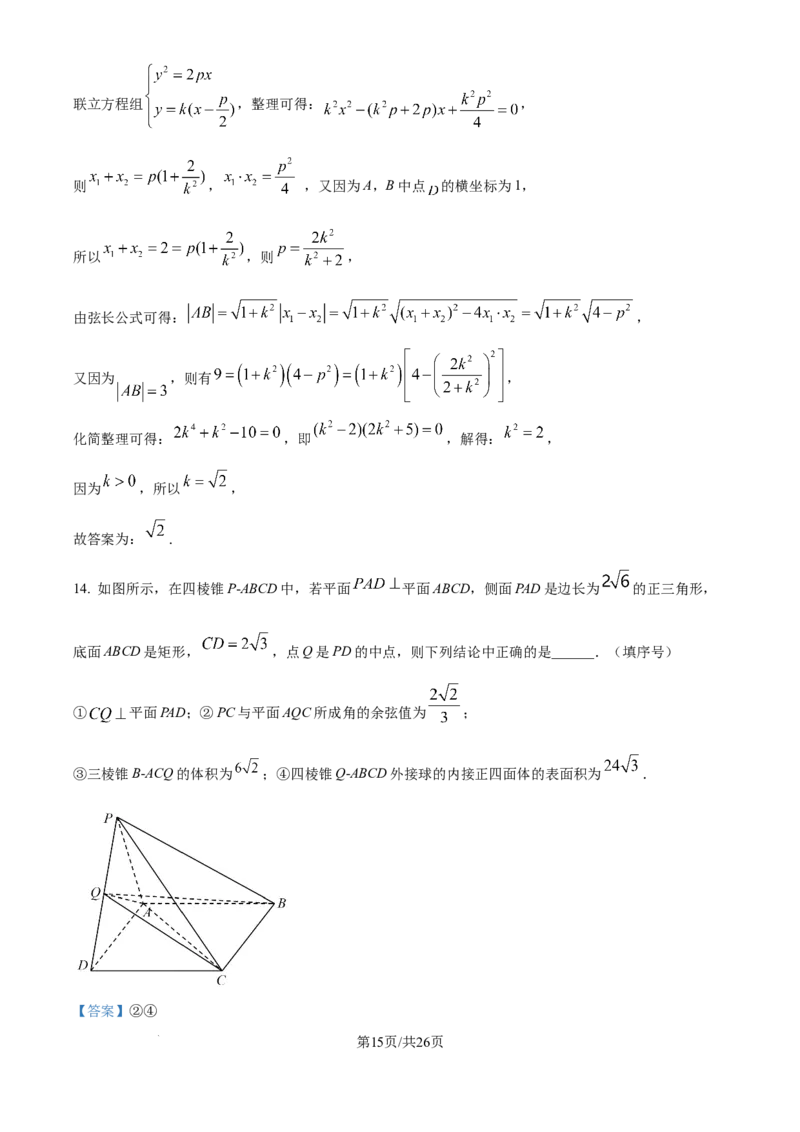
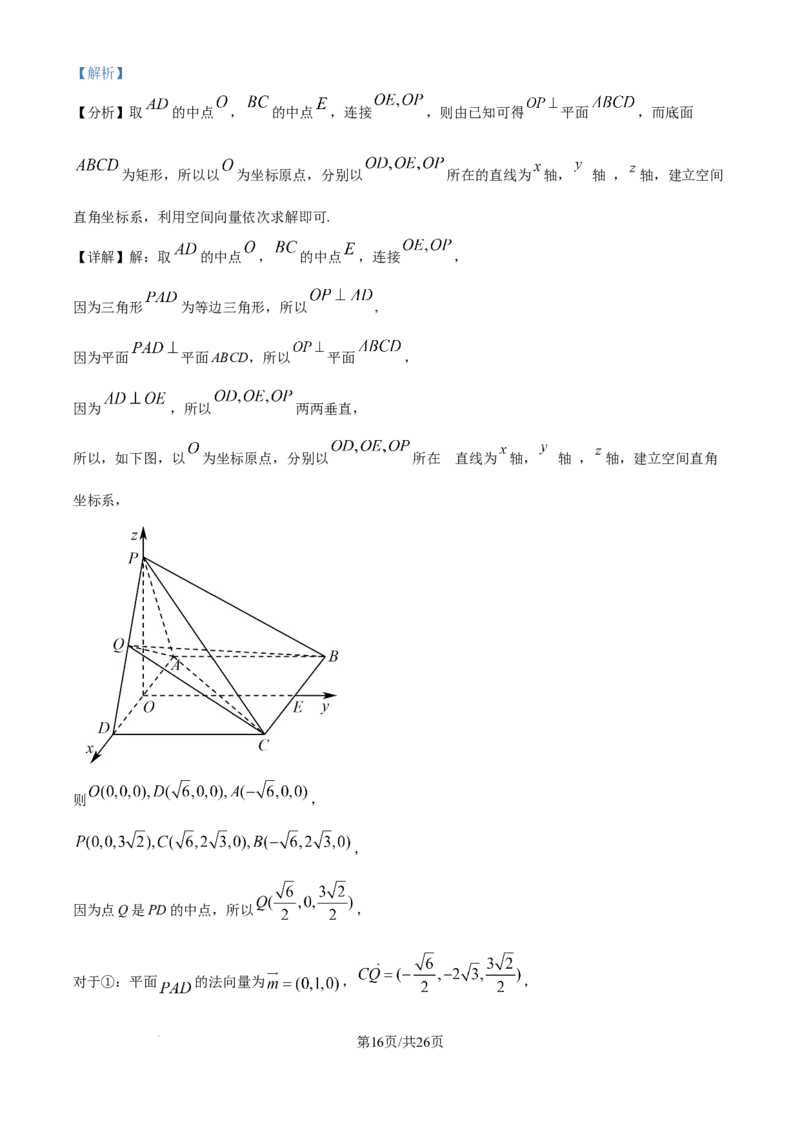
14. 如图所示,在四棱锥P-ABCD中,若平面 平面ABCD,侧面PAD是边长为 的正三角形,
底面ABCD是矩形, ,点Q是PD的中点,则下列结论中正确的是______.(填序号)
① 平面PAD;②PC与平面AQC所成角的余弦值为 ;
③三棱锥B-ACQ的体积为 ;④四棱锥Q-ABCD外接球的内接正四面体的表面积为 .
【答案】②④
第15页/共26页
学科网(北京)股份有限公司【解析】
【分析】取 的中点 , 的中点 ,连接 ,则由已知可得 平面 ,而底面
为矩形,所以以 为坐标原点,分别以 所在的直线为 轴, 轴 , 轴,建立空间
直角坐标系,利用空间向量依次求解即可.
【详解】解:取 的中点 , 的中点 ,连接 ,
因为三角形 为等边三角形,所以 ,
因为平面 平面ABCD,所以 平面 ,
因为 ,所以 两两垂直,
的
所以,如下图,以 为坐标原点,分别以 所在 直线为 轴, 轴 , 轴,建立空间直角
坐标系,
则 ,
,
因为点Q是PD的中点,所以 ,
对于①:平面 的法向量为 , ,
第16页/共26页
学科网(北京)股份有限公司所以 与 不共线,所以 与平面 不垂直,故①不正确;
对于②: ,
设平面 的法向量为 ,则
,
令 ,则 ,
所以 ,
设PC与平面AQC所成角为 ,
则 ,
所以 ,所以②正确;
对于③:三棱锥 的体积为
,所以③不正确;
对于④:设四棱锥 外接球的球心为 ,则 ,
所以 ,
解得 ,即 为矩形 对角线的交点,
所以四棱锥 外接球的半径为 ,
设四棱锥 外接球的内接正四面体的棱长为 ,
第17页/共26页
学科网(北京)股份有限公司将四面体拓展成正方体,其中正四面体棱为正方体面的对角线,
故正方体的棱长为 ,所以 ,得 ,
所以正四面体的表面积为 ,所以④正确.
故选:②④.公众号:高中试卷君
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 春夏之交因昼夜温差大,细菌、病毒等活跃,是流感高发季节.某校高二年级某组团统计了流感暴发
前的半个月与流感暴发后的半个月的学生请假情况,得到如下数据:
因发烧请假 非发烧请假 合计
流感暴发前 10 30
流感暴发后 30
合计 70
(1)完成 列联表,并依据 的独立性检验,判断能否认为流感暴发对请假的同学中发烧的人
数有影响.
(2)后经过了解,在全校因发烧请假的同学中男生占比为 ,且 的因发烧请假的男生需要输液
治疗, 的因发烧请假的女生需要输液治疗.学校随机选择一名因发烧请假在医院输液的同学进行慰问,
求这名同学是女生的概率.
附: .
0.05 0.01 0.001
3.841 6.635 10.828
【答案】(1)表格见解析,有影响
(2)
【解析】
第18页/共26页
学科网(北京)股份有限公司【分析】(1)根据题意完成 列联表,计算 ,再与临界值比较即可;(2)利用条件概率公式求解.
【小问1详解】
零假设为 :流感暴发与请假的同学中发烧的人数之间相互独立.
完成列联表如下所示.
因发烧请假 非发烧请假 合计
流感暴发前 10 20 30
流感暴发后 30 10 40
合计 40 30 70
根据列联表中的数据,经计算得
.
所以我们推断 不成立,即可以认为流感暴发对请假的同学中发烧的人数有影响.
【小问2详解】
设 事件表示请假的同学为女生, 事件表示需要输液治疗,
, ,
则 .
所以这名同学是女生的概率为 .
16. 已知 为各项均为正数的等比数列,且 , .
(1)求数列 的通项公式;
(2)令 ,求数列 前n项和 .
【答案】(1)
第19页/共26页
学科网(北京)股份有限公司(2)
【解析】
【分析】(1)利用基本量法,求出首项和公比,即可求解.
(2)利用错位相减法,即可求解.
【小问1详解】
设等比数列 公比 为
【小问2详解】
17. 为建设“书香校园”,学校图书馆对所有学生开放图书借阅,可借阅的图书分为“期刊杂志”与“文献书籍”
两类,已知该校小明同学的图书借阅规律如下:第一次随机选择一类图书借阅,若前一次选择借阅“期刊
第20页/共26页
学科网(北京)股份有限公司杂志”,则下次也选择借阅“期刊杂志”的概率为 ,若前一次选择借阅“文献书籍”,则下次选择借阅“期刊
杂志”的概率为 .
(1)求小明同学在两次借阅过程中恰有一次借阅“期刊杂志”的概率;
(2)求小明同学在两次借阅过程中,第二次借阅的是“文献书籍”的概率.
【答案】(1)
(2)
【解析】
【分析】(1)利用互斥事件的概率公式与条件概率的乘法公式即可得解;
(2)利用全概率公式求解.
【小问1详解】
用 , 分别表示第一次、第二次借阅“期刊杂志”,用 , 表示第一次、第二次借阅“文献书籍”.
则 , , , , .
记两次借阅过程中恰有一次借阅“期刊杂志”为事件 ,则
.
【小问2详解】
设第二次借阅“文献书籍”为事件 ,则:
.
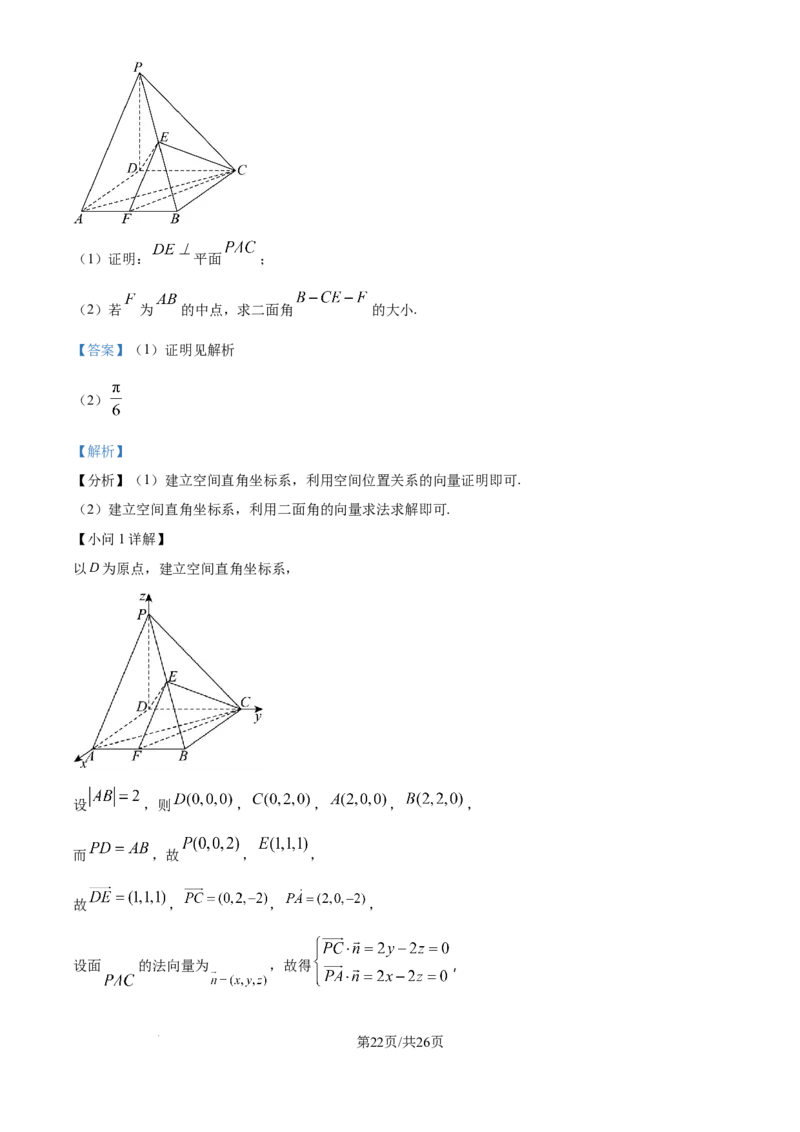
18. 如图,四棱锥 的底面是正方形, 平面 , , 为 的中点.
第21页/共26页
学科网(北京)股份有限公司(1)证明: 平面 ;
(2)若 为 的中点,求二面角 的大小.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)建立空间直角坐标系,利用空间位置关系的向量证明即可.
(2)建立空间直角坐标系,利用二面角的向量求法求解即可.
【小问1详解】
以 为原点,建立空间直角坐标系,
设 ,则 , , , ,
而 ,故 , ,
故 , , ,
设面 的法向量为 ,故得 ,
第22页/共26页
学科网(北京)股份有限公司令 ,解得 , ,故得 ,
显然 与 平行,故 平面 得证.
【小问2详解】
易知 , , , ,
, ,设面 的法向量为 ,
故有 ,令 ,解得 , ,故 ,
设面 的法向量为 ,故得 ,
令 ,解得 , ,故 ,
设二面角 为 ,结合图象可知 ,
故 ,
故 ,即二面角 的大小为 .
19. 已知函数 .
(1)讨论函数 的单调性;
(2)设函数 有两个不同的零点 ,
(i)求实数 的取值范围:
(ⅱ)若 满足 ,求实数 的最大值.
【答案】(1)答案见解析;
第23页/共26页
学科网(北京)股份有限公司(2)(i) ;(ⅱ) .
【解析】
【分析】(1)求导 ,分类讨论参数 和 时,函数的单调性即可.
(2)(ⅰ)利用参数分离可得 ,令 ,利用导数研究函数的单调性,极值,数
形结合即可;
(ⅱ)由已知 ,设 ,可得 ,设 ,利用
导数研究函数的单调性,可求额 ,再利用 的单调性可求得 ,
进而求得结果.
【小问1详解】
函数 的定义域为 ,求导得 ,
当 时, 恒成立,函数 在 上单调递增;
当 时,由 ,得 ,由 ,得 ,
即函数 在 上单调递增,在 上单调递减,
所以当 时, 的递增区间是 ,无递减区间;
当 时, 的递增区间是 ,递减区间是 .
【小问2详解】
第24页/共26页
学科网(北京)股份有限公司(ⅰ)由 ,得 ,令 ,求导得 ,
当 时, ,当 时, ,
则函数 在 上单调递增,在 上单调递减, ,
而当 时, 恒成立,且 ,
由 有两个零点,即方程 有两个不等的正根,亦即直线 与 的图象有两个公共点,
因此 ,即 ,
所以实数 的取值范围是 .
(ⅱ)由 ,得 ,且 ,
不妨设 ,将 代入 ,
得 ,即 ,
令 ,求导得 ,令 ,
求导得 ,则函数 在 上单调递减,
有 ,即 ,函数 在 上单调递减,
由 ,得 ,则 ,
第25页/共26页
学科网(北京)股份有限公司因此函数 在 上单调递减,即 ,
于是 ,有 ,则 ,
又 ,令 , ,
由(ⅰ)知, 在 上递增,而 ,因此 在 上递增,
则 ,即 ,解得 ,
所以a的最大值是 .
【点睛】思路点睛:已知函数的零点或方程的根的情况,求解参数的取值范围问题的本质都是研究①转化,
即通过构造函数,把问题转化成所构造函数的零点问题;
②列式,即根据函数的零点存在定理或结合函数的图象列出关系式;
③得解,即由列出的式子求出参数的取值范围.
第26页/共26页
学科网(北京)股份有限公司