文档内容
5.3.1 函数的单调性与导数
基础练
一、单选题
1.下列函数中,在其定义域上为增函数的是( )
A. B. C. D.
2.函数 的单调递减区间为( )
A. B. C. D.
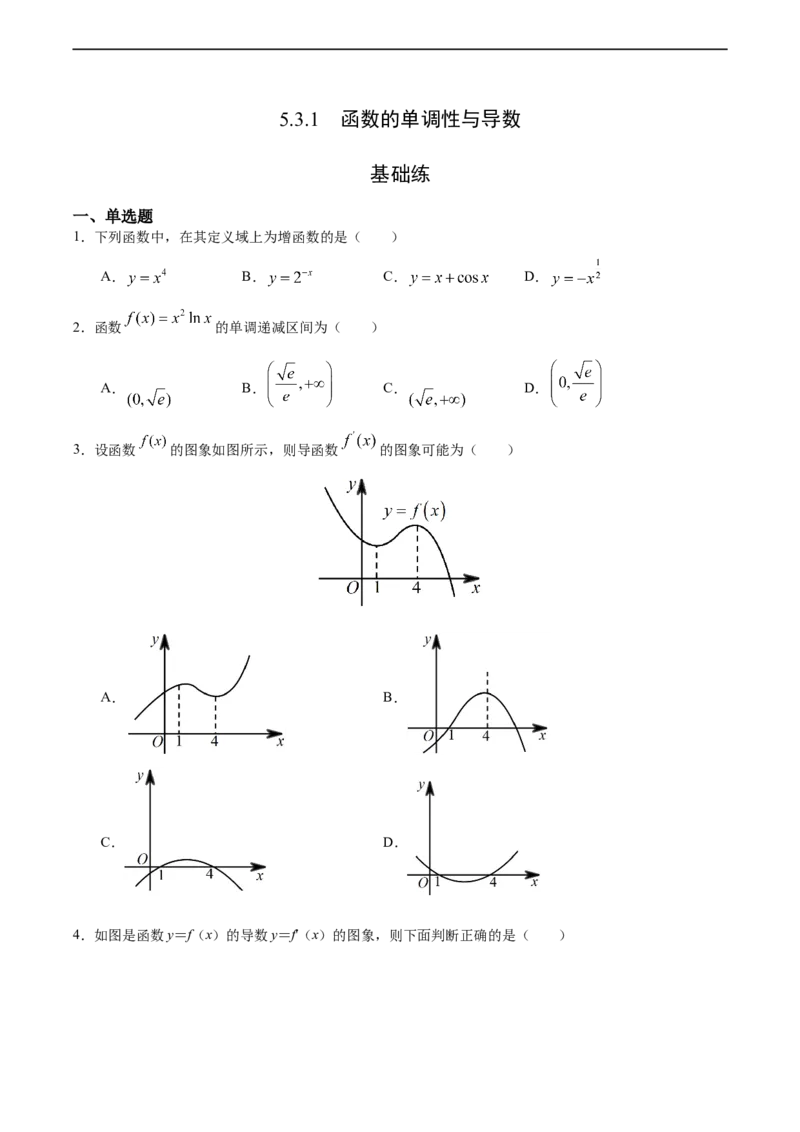
3.设函数 的图象如图所示,则导函数 的图象可能为( )
A. B.
C. D.
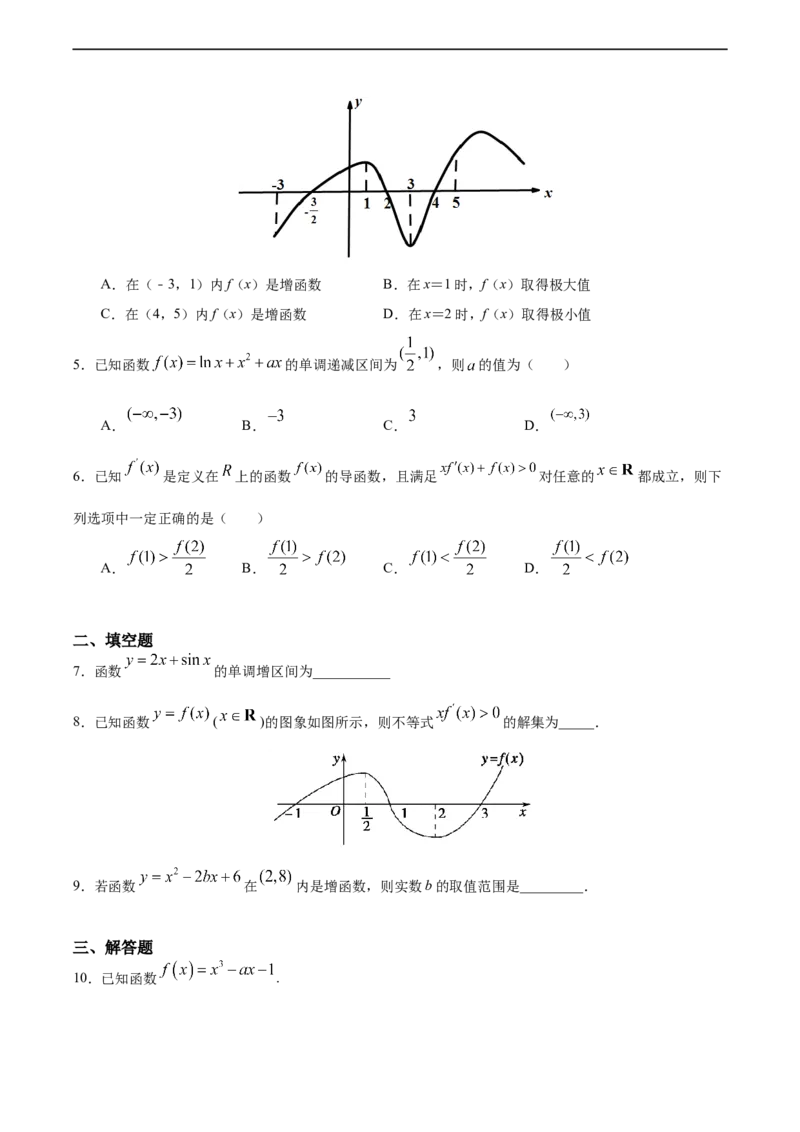
4.如图是函数y=f(x)的导数y=f'(x)的图象,则下面判断正确的是( )A.在(﹣3,1)内f(x)是增函数 B.在x=1时,f(x)取得极大值
C.在(4,5)内f(x)是增函数 D.在x=2时,f(x)取得极小值
5.已知函数 的单调递减区间为 ,则 的值为( )
A. B. C. D.
6.已知 是定义在 上的函数 的导函数,且满足 对任意的 都成立,则下
列选项中一定正确的是( )
A. B. C. D.
二、填空题
7.函数 的单调增区间为___________
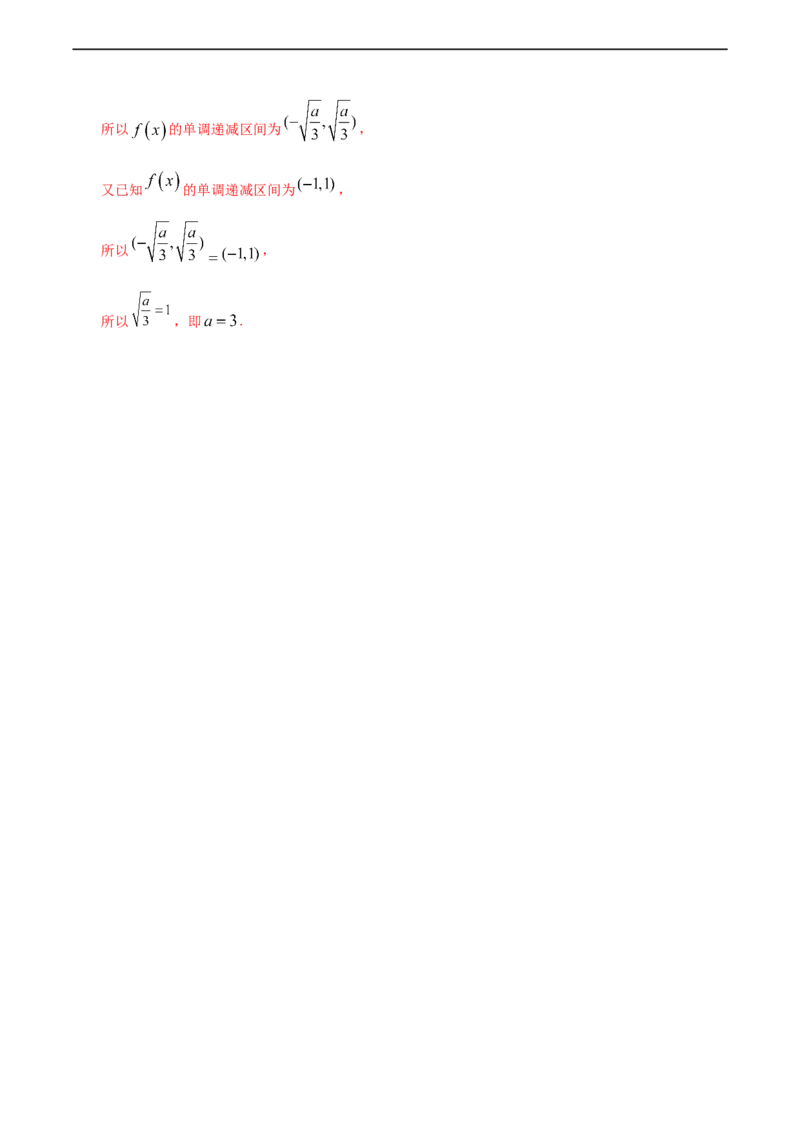
8.已知函数 ( )的图象如图所示,则不等式 的解集为_____.
9.若函数 在 内是增函数,则实数b的取值范围是_________.
三、解答题
10.已知函数 .(1)若 在区间 上为增函数,求a的取值范围.
(2)若 的单调递减区间为 ,求a的值.参考答案
1.【答案】C
【解析】对于A选项,函数 为偶函数,在 上递增,在 上递减;
对于B选项,函数 在 上递减;
对于C选项, 在 上恒成立,则函数 在其定义域 上递增;
对于D选项,函数 在 上递减.
故选C.
2.【答案】D
【解析】由题意得,函数 的定义域为 ,
.
令 ,得 ,解得 ,
故函数 的单调递减区间为 .
故选D
3.【答案】C
【解析】∵ 在 , 上为减函数,在 上为增函数,
∴当 或 时, ;当 时, .
故选C.
4.【答案】C
【解析】根据题意,依次分析选项:
对于A,在(﹣3, )上,f′(x)<0,f(x)为减函数,A错误;对于B,在( ,2)上,f′(x)>0,f(x)为增函数,x=1不是f(x)的极大值点,B错误;
对于C,在(4,5)上,f′(x)>0,f(x)为增函数,C正确;
对于D,在( ,2)上,f′(x)>0,f(x)为增函数,在(2,4)上,f′(x)<0,f(x)为减函
数,则在x=2时f(x)取得极大值,D错误;
故选C.
5.【答案】B
【解析】由题得 的解集为 ,
所以不等式 的解集为 ,
所以
故选B
6.【答案】D
【解析】令 ,则 ,故 为 上的增函数,
所以 即 ,
故选D.
7.【答案】
【解析】 , ,
∴ 在 上恒成立,所以函数的单调增区间为 ,
故填
8.【答案】【解析】由 的图象可知 在 和 上单调递增,在 上单调递减,
所以 的解集为 , 的解集为 ,
由 得 或 ,
所以 的解集为 ,
故填
9.【答案】
【解析】由题意得 在 内恒成立,
即 在 内恒成立,
所以 .
故填
10.【答案】(1) ;(2)3.
【解析】(1)因为 ,且 在区间 上为增函数,
所以 在 上恒成立,即 在(1,+∞)上恒成立,
所以 在 上恒成立,所以 ,即a的取值范围是
(2)由题意知 .因为 ,所以 .
由 ,得 ,所以 的单调递减区间为 ,
又已知 的单调递减区间为 ,
所以 ,
所以 ,即 .