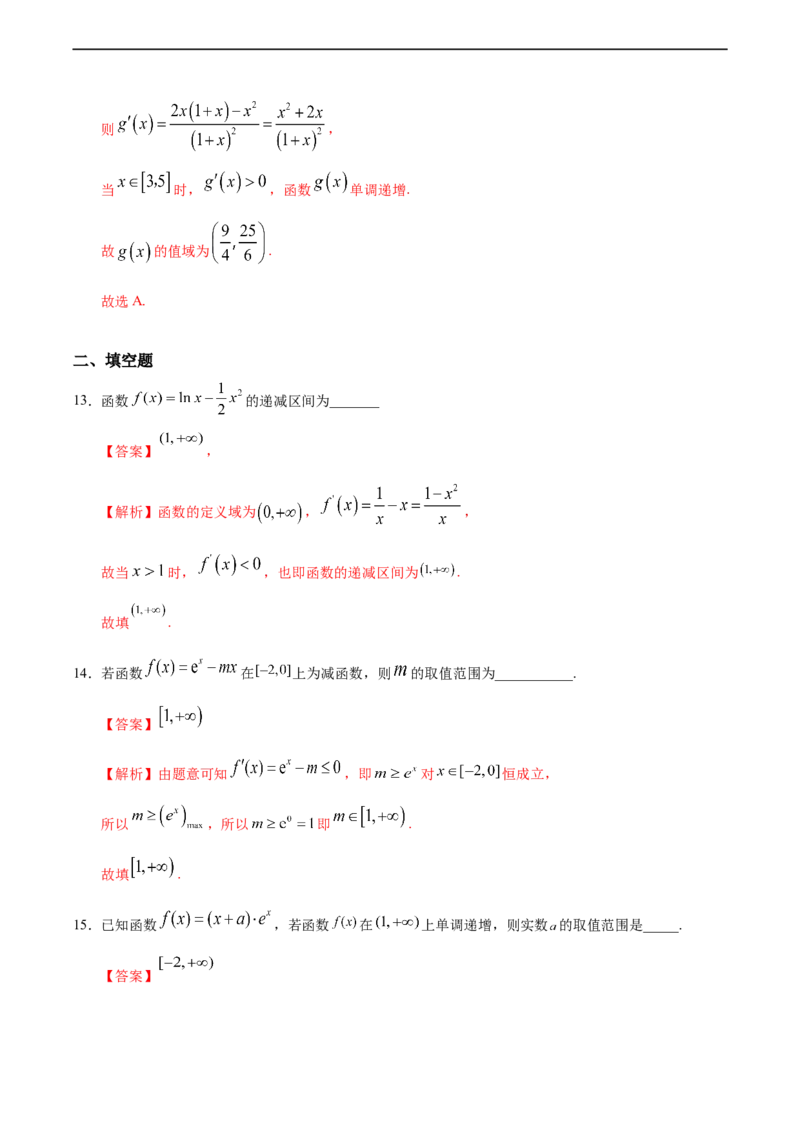文档内容
111公式章 1 节 1课时同步练
5.3.1 函数的单调性与导数
一、单选题
1.下列函数在区间 上是增函数的是( )
A. B. C. D.
【答案】A
【解析】根据题意,依次分析选项,
对于A, ,其导数 ,当 时,有 恒成立,则函数
在 上为增函数,符合题意;
对于B, ,其导数为 ,在 上, ,则函数 在 上
为减函数,不符合题意;
对于C, ,其导数为 ,当 时,有 恒成立,则函数
在 上为减函数,不符合题意;
对于D, ,为二次函数,在 上为减函数,不符合题意;
故选A.
2.函数 的单调递减区间是( )
A. B. C. D.
【答案】C
【解析】由题意,可得 ,
令 ,即 ,解得 ,即函数的递减区间为 .故选C
3.已知函数 ,则 ( )
A.在 上递增 B.在 上递增
C.在 上递减 D.在 上递减
【答案】A
【解析】依题意,
当 时, ,函数 单调递增;
当 时, ,函数 单调递减.
对照选项可知:函数 在 上递增.
故选A.
4.函数 的单调减区间是( )
A. B. C. D.
【答案】D
【解析】由题,对 函数定义域 ,
求导可得 ,
令 ,可得 .
故选D.
5.函数 的单调递增区间( )
A. B. C. D.【答案】C
【解析】由题得 ,
解不等式 ,
所以 .
所以函数的单调增区间为 .
故选C
6.函数 的单调递增区间是( )
A. B. C.(1,4) D.(0,3)
【答案】B
【解析】 , ,解不等式 ,解得 ,
因此,函数 的单调递增区间是 ,
故选B.
7.若函数 ,则函数 的单调递减区间为( )
A. B.
C.(0,3) D.
【答案】C
【解析】函数 的定义域为: ,
因为 ,
令 并且 ,得: ,
所以函数 的单调递减区间为(0,3).故选C.
8.若函数 在区间 上单调递增,则实数 的取值范围是( )
A. B. C. D.
【答案】D
【解析】 函数 在区间 单调递增,
在区间 上恒成立,则 ,而 在区间 上单调递减,
, 的取值范围是
故选D.
9.已知函数 在 上不单调,则 的取值范围是( )
A. B. C. D.
【答案】C
【解析】 .因为 在 上不单调.
所以 在 上有解,
又 在 上单调递减,
所以 , ,
故 .
故选C
10.如果函数y=f(x)在区间I上是增函数,且函数 在区间I上是减函数,那么称函数y=f(x)是区
间I上的“缓增区间”,区间I叫做“缓增区间”.若函数 是区间I上的“缓增区间”,
则“缓增区间”I为( )A.[1,+∞) B.[0, ] C.[0,1] D.[1, ]
【答案】D
【解析】因为函数 的对称轴为x=1,
所以函数y=f(x)在区间[1,+∞)上是增函数,
又当x≥1时, ,
令 (x≥1),则 ,
由g′(x)≤0得 ,
即函数 在区间 上单调递减,
故“缓增区间”I为 ,
故选D.
11.已知函数 对于任意的 满足 ,其中 是函数
的导函数,则下列不等式成立的是( )
A. B.
C. D.
【答案】B
【解析】由题意构造函数 ,
则
.对于任意的 满足 ,
故 ,当 时, ,
当 时, ,
因此 在 单调递减,在 单调递增.
又因为 ,因此 ,
因此有 ,
化简得 .
故选B
12.若函数 在区间 上不是单调函数,则实数 的取值范围是( )
A. B. C. D.
【答案】A
【解析】因为函数 在区间 上不是单调函数,
所以 在区间 上有解,且不是重解.
即 可得 ,
令 , ,则 ,
当 时, ,函数 单调递增.
故 的值域为 .
故选A.
二、填空题
13.函数 的递减区间为_______
【答案】 ,
【解析】函数的定义域为 , ,
故当 时, ,也即函数的递减区间为 .
故填 .
14.若函数 在 上为减函数,则 的取值范围为___________.
【答案】
【解析】由题意可知 ,即 对 恒成立,
所以 ,所以 即 .
故填 .
15.已知函数 ,若函数 在 上单调递增,则实数 的取值范围是_____.
【答案】【解析】因为 ,所以 ,
函数 在 上单调递增,可知 在 上恒成立,
即 ,所以 ,即 ,则实数 的取值范围是 .
故填 .
16.定义域为 的函数 满足 ,且 的导函数 ,则不等式 的解集
为 _____________.
【答案】 .
【解析】令 ,因为 ,所以 .
所以 为单调增函数.因为 ,所以 .
所以当 时, ,即 ,得 ,解集为
故填
17.已知函数 ( 为自然对数的底数),若 ,则实数 的取值
范围是___________.
【答案】
【解析】令 ,则 为奇函数,且为增函数,所以
故填
18.已知函数 在区间 上是单调函数,则实数t的取值范围______.【答案】
【解析】函数 的定义域为 , .
令 ,可得 或 ;令 ,可得 .
所以,函数 的单调增区间为 和 ,单调递减区间为 .
由于函数 在 上单调,则 为以上三个区间的子集.
①若 ,可得 ;
②若 ,可得 ,解得 ;
③若 ,则 .
因此,实数 的取值范围是 .
故填 .
三、解答题
19.已知函数 .
(1)求在 处的切线的方程;
(2)求函数的单调区间.【解析】(1)函数 ,则 ,故在 处的切线的斜率 ,故切
线的方程是 ,即 ;
(2)令 ,得 或 ,令 ,得 ,
故函数的单调增区间是 ,单调减区间是 .
20.已知函数 的导函数 的一个零点为 .
(1)求a的值;
(2)求函数 的单调区间.
【解析】(1) ,
由 ,得 .
(2)由(1)得 ,
则 .
令 ,得 或 .
当 时, ;
当 时, 或 .
因此 的单调递增区间是 ,单调递减区间是 .
21.已知函数 , .
(1)若 与 在 处相切,求 的表达式;
(2)若 在 上是减函数,求实数 的取值范围.【解析】(1) ,
,
又 与 在 处相切,
,
解得: ,
,
即 ,
解得: ,
;
(2) 在 上是减函数,
即 在 上是减函数,
在 上恒成立,
即 在 上恒成立,
则 在 上恒成立,
又 在 上单调递增,
,
,
解得: ,即实数 的取值范围是 .
22.已知函数 .
(1)若函数 在区间 上是单调函数,求实数a的取值范围;
(2)讨论函数 的单调性.
【解析】(1)由题意得, .
①当 时, ,函数 单调递减.
②当 时,令 ,
∵函数 在区间 上是单调函数,
∴ 在区间 上恒成立,
∴ 在区间 上恒成立.
令 ,
∵ ,当且仅当 时取等号,∴ ,
∴当 时,函数 单调递增,
∴实数a的取值范围是 .
(2)由(1)可知,①当 时, ,函数 在 上单调递减,
②当 时,函数 在 上单调递增,
③当 时,由 ,解得 或 ,
∴函数 在 , 上单调递增,
在 上单调递减.