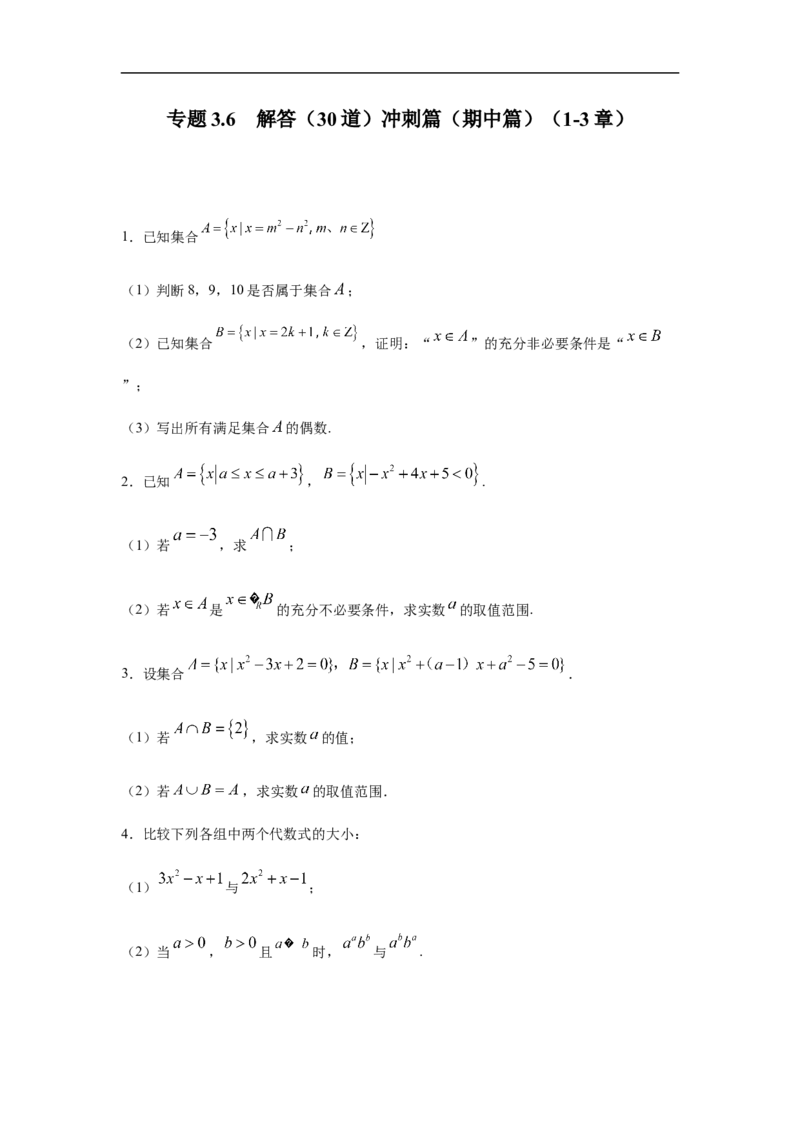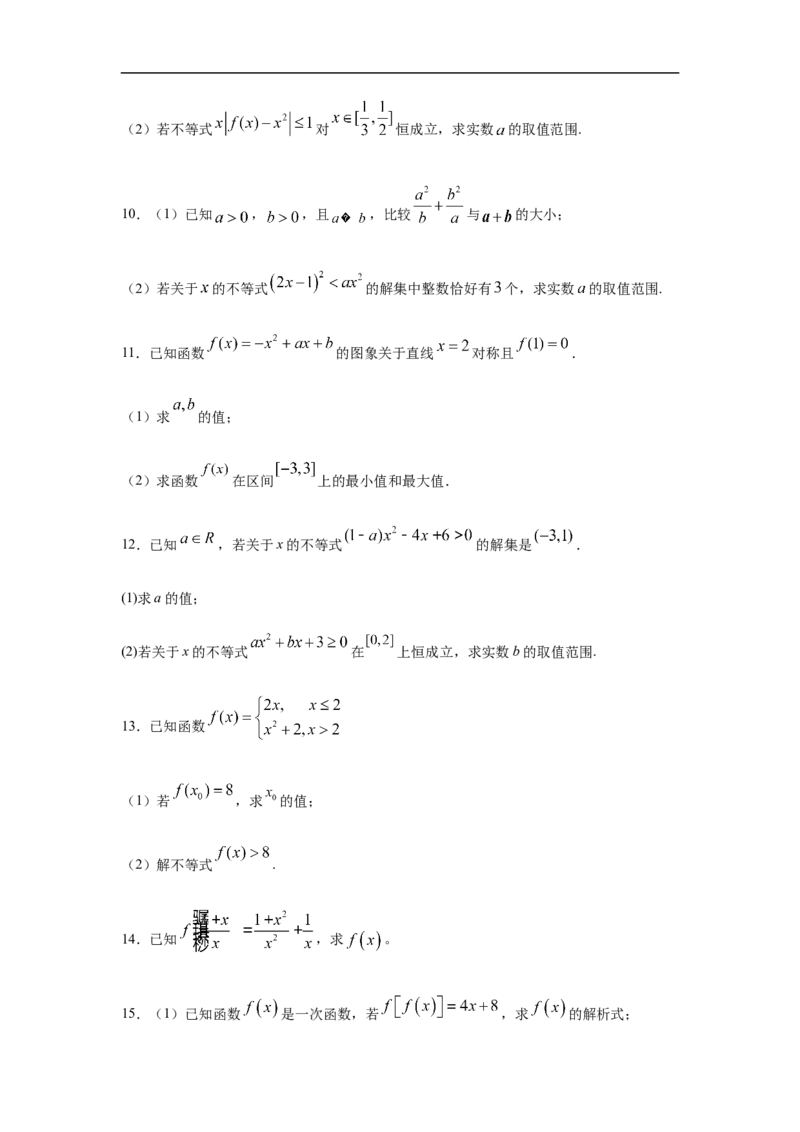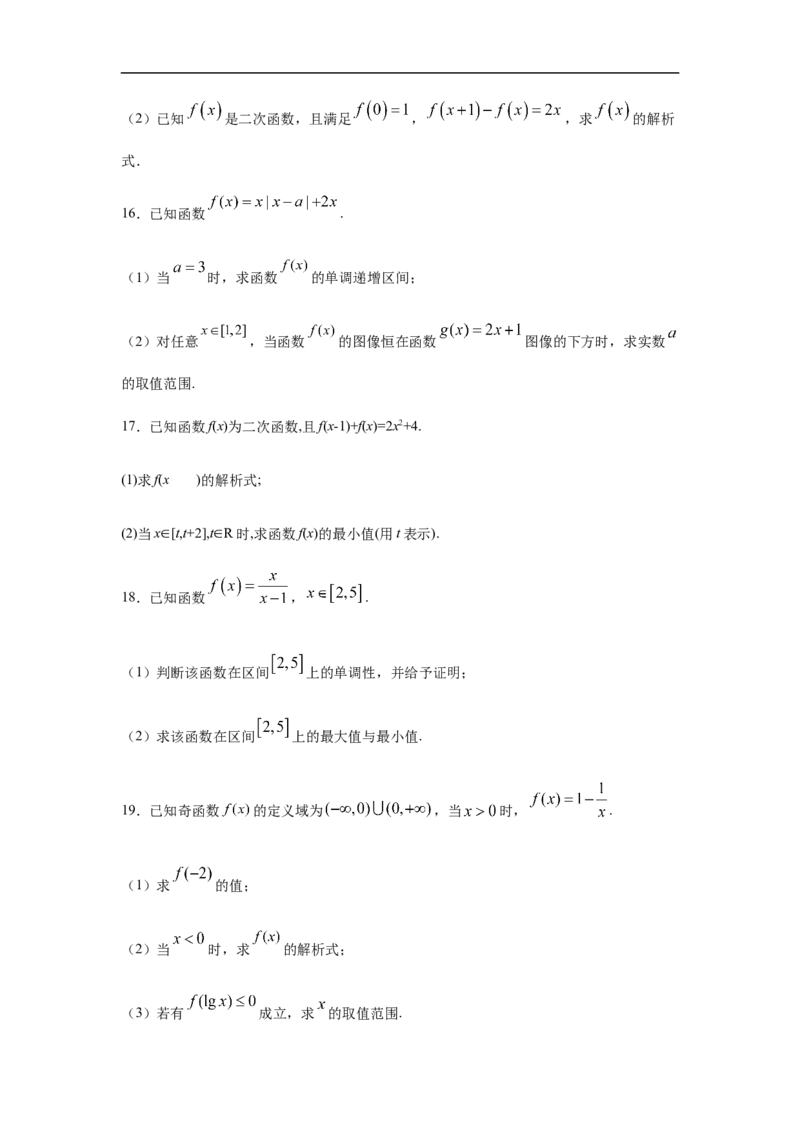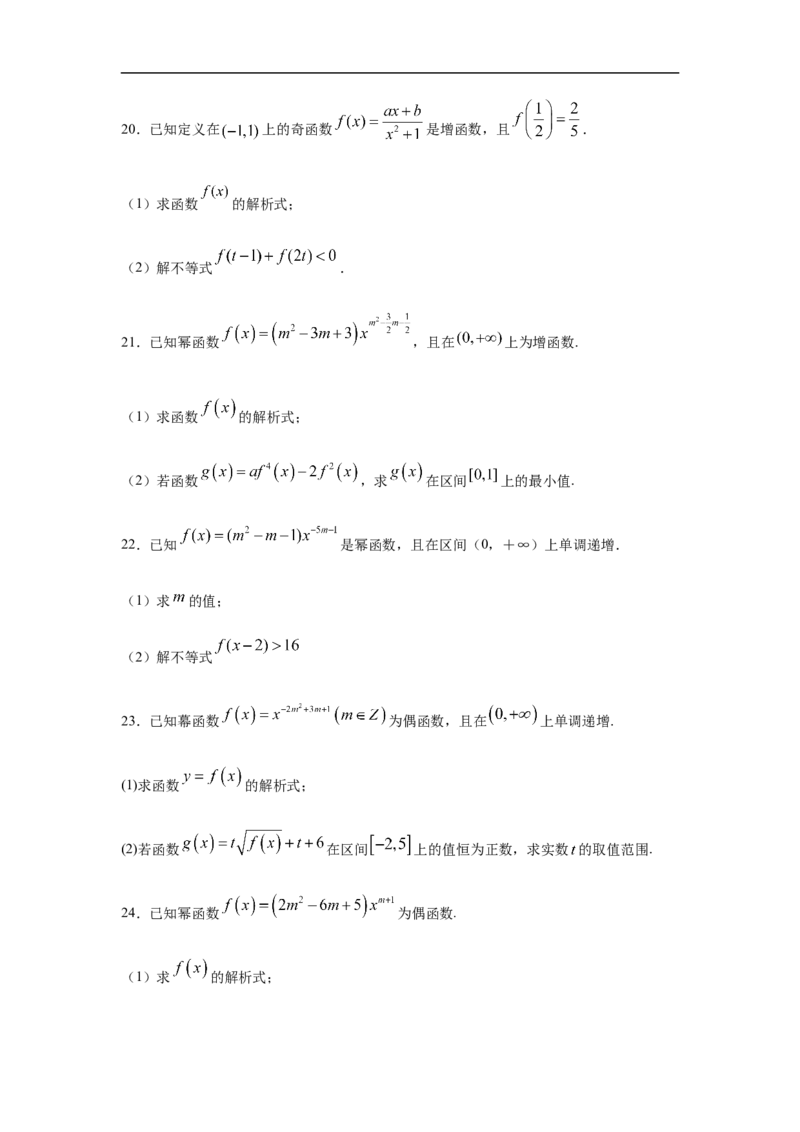文档内容
专题3.6 解答(30道)冲刺篇(期中篇)(1-3 章)
1.已知集合
(1)判断8,9,10是否属于集合 ;
(2)已知集合 ,证明:“ ”的充分非必要条件是“
”;
(3)写出所有满足集合 的偶数.
2.已知 , .
(1)若 ,求 ;
(2)若 是 的充分不必要条件,求实数 的取值范围.
3.设集合 .
(1)若 ,求实数 的值;
(2)若 ,求实数 的取值范围.
4.比较下列各组中两个代数式的大小:
(1) 与 ;
(2)当 , 且 时, 与 .5.已知 , .
(1)求证: ;
(2)若 ,求ab的最小值.
6.已知 , , 为正实数,且 ,证明:
(1) ;
(2) .
7.已知函数 .
(1)求不等式 的解集;
(2)正数 满足 ,证明: .
8.已知函数 .
(1)求不等式 的解集 ;
(2)若 为集合 中的最大元素,且 ,求 的最小值.
9.已知 ,函数 .
(1)若 ,且函数 的定义域和值域均为 ,求实数 的值;(2)若不等式 对 恒成立,求实数 的取值范围.
10.(1)已知 , ,且 ,比较 与 的大小;
(2)若关于 的不等式 的解集中整数恰好有 个,求实数 的取值范围.
11.已知函数 的图象关于直线 对称且 .
(1)求 的值;
(2)求函数 在区间 上的最小值和最大值.
12.已知 ,若关于x的不等式 的解集是 .
(1)求a的值;
(2)若关于x的不等式 在 上恒成立,求实数b的取值范围.
13.已知函数
(1)若 ,求 的值;
(2)解不等式 .
14.已知 ,求 。
15.(1)已知函数 是一次函数,若 ,求 的解析式;(2)已知 是二次函数,且满足 , ,求 的解析
式.
16.已知函数 .
(1)当 时,求函数 的单调递增区间;
(2)对任意 ,当函数 的图像恒在函数 图像的下方时,求实数
的取值范围.
17.已知函数f(x)为二次函数,且f(x-1)+f(x)=2x2+4.
(1)求f(x )的解析式;
(2)当x∈[t,t+2],t∈R时,求函数f(x)的最小值(用t表示).
18.已知函数 , .
(1)判断该函数在区间 上的单调性,并给予证明;
(2)求该函数在区间 上的最大值与最小值.
19.已知奇函数 的定义域为 ,当 时, .
(1)求 的值;
(2)当 时,求 的解析式;
(3)若有 成立,求 的取值范围.20.已知定义在 上的奇函数 是增函数,且 .
(1)求函数 的解析式;
(2)解不等式 .
21.已知幂函数 ,且在 上为增函数.
(1)求函数 的解析式;
(2)若函数 ,求 在区间 上的最小值.
22.已知 是幂函数,且在区间(0,+∞)上单调递增.
(1)求 的值;
(2)解不等式
23.已知幕函数 为偶函数,且在 上单调递增.
(1)求函数 的解析式;
(2)若函数 在区间 上的值恒为正数,求实数 的取值范围.
24.已知幂函数 为偶函数.
(1)求 的解析式;(2)若函数 在区间(2,3)上为单调函数,求实数a的取值范围.
25.已知幂函数 满足:
(1)在区间 上为增函数;
(2)对任意的 都有 .
求同时满足(1)(2)的幂函数 的解析式,并求当 时, 的值域.
26.已知幂函数
(1)求 的解析式;
(2)(i)若 图像不经过坐标原点,直接写出函数 的单调区间.
(ii)若 图像经过坐标原点,解不等式 .
27.已知幂函数 为偶函数.
(1)求 的解析式;
(2)若 ,求实数a的取值范围.
28.已知幂函数 在 上单调递增.
(1)求实数 的值;
(2)若 ,求实数 的取值范围.29.定义在 上的函数 ,满足 ,且当
时, .
(1)求 的值.
(2)求证: .
(3)求证: 在 上是增函数.
(4)若 ,解不等式 .
(5)比较 与 的大小.
30.函数 的定义域为 ,且对一切 ,都有 ,
当 时,总有 .
(1)求 的值;
(2)判断 单调性并证明;
(3)若 ,解不等式 .