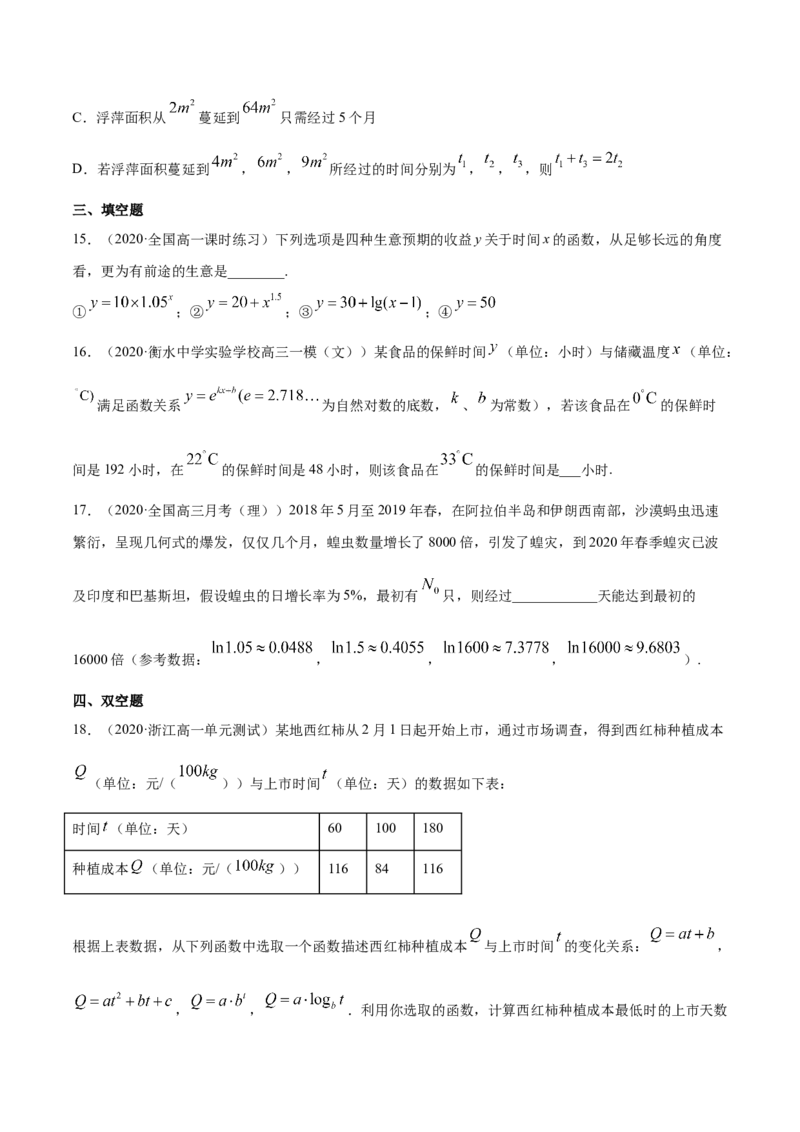文档内容
建立数学模型解决实际问题
主要命题方向
1. 函数模型的增长差异;2. 巧用图象比较大小;3. 几种函数模型的应用;4. 一次函数与分段函数模型
问题;5. 二次函数模型问题;6. 指数型、对数型函数模型应用问题;7. 建模思想——函数模型的确定;
8. 指数、对数函数型实际应用问题.
配套提升训练
一、单选题
1.(2020·全国高三课时练习(理))在新冠肺炎疫情防控期间,某超市开通网上销售业务,每天能完成
1200份订单的配货,由于订单量大幅增加,导致订单积压.为解决困难,许多志愿者踊跃报名参加配货工
作.已知该超市某日积压500份订单未配货,预计第二天的新订单超过1600份的概率为0.05,志愿者每人
每天能完成50份订单的配货,为使第二天完成积压订单及当日订单的配货的概率不小于0.95,则至少需要
志愿者( )
A.10名 B.18名 C.24名 D.32名
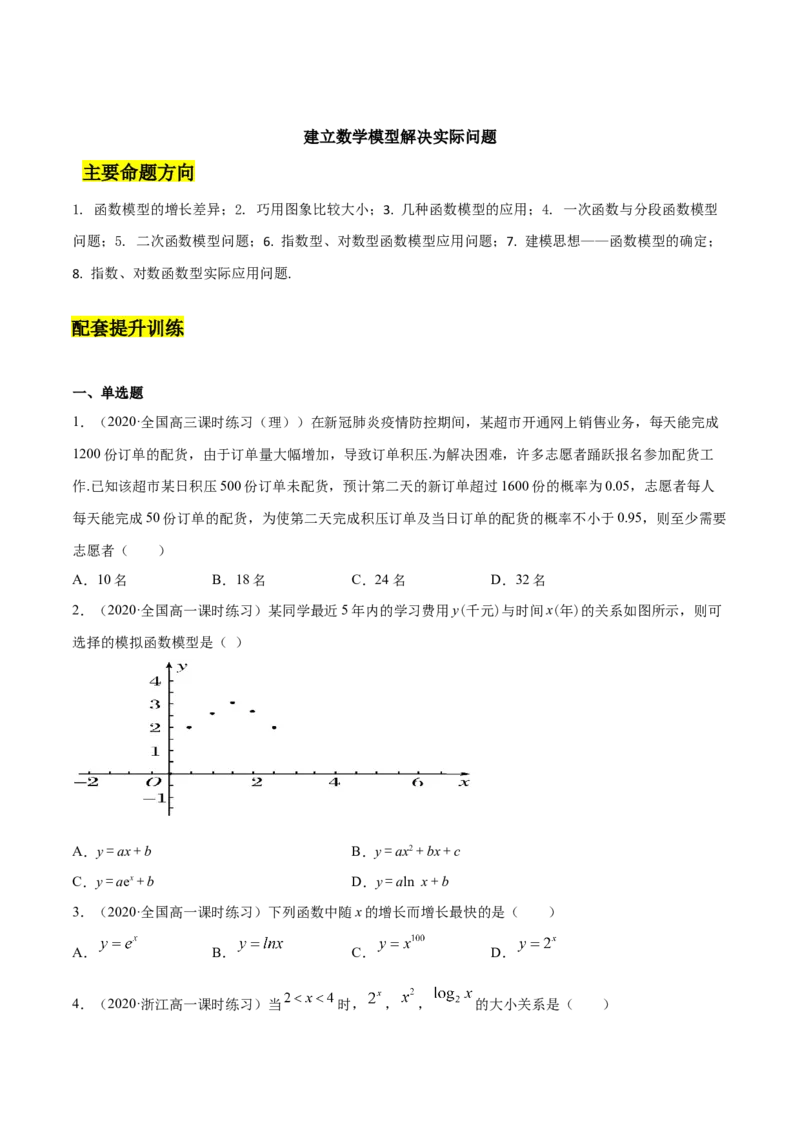
2.(2020·全国高一课时练习)某同学最近5年内的学习费用y(千元)与时间x(年)的关系如图所示,则可
选择的模拟函数模型是( )
A.y=ax+b B.y=ax2+bx+c
C.y=aex+b D.y=aln x+b
3.(2020·全国高一课时练习)下列函数中随x的增长而增长最快的是( )
A. B. C. D.
4.(2020·浙江高一课时练习)当 时, , , 的大小关系是( )A. B.
C. D.
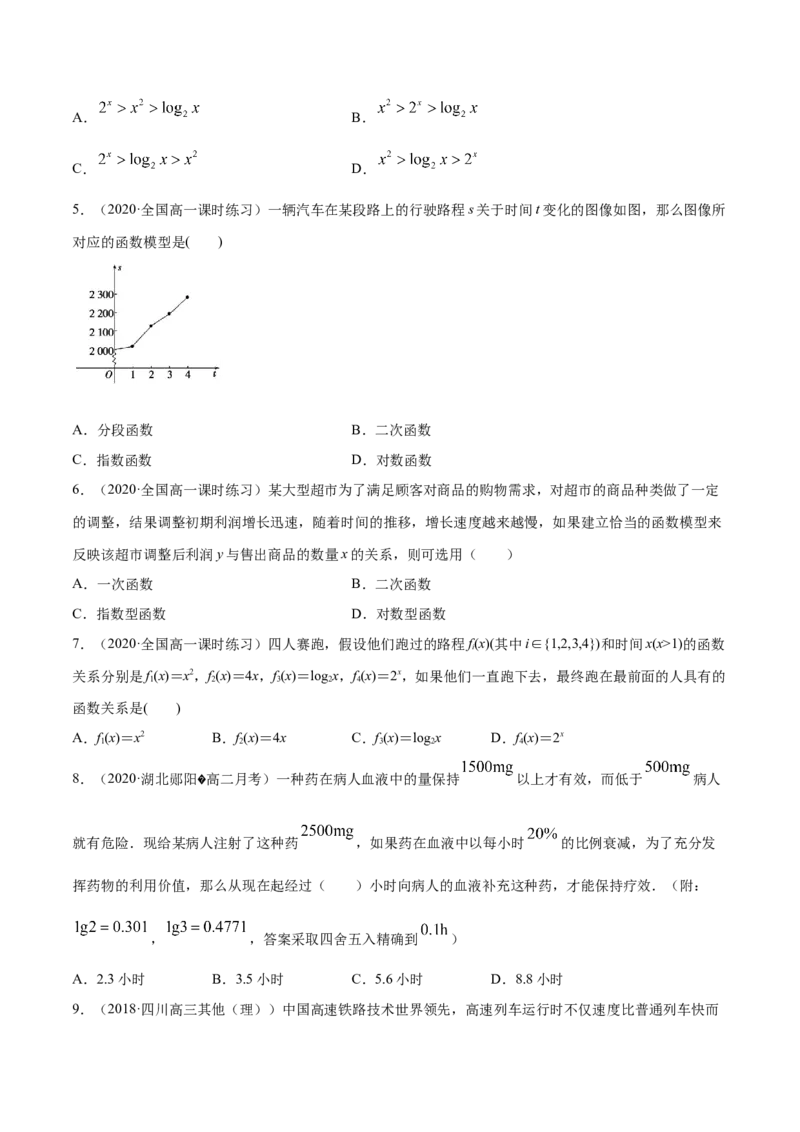
5.(2020·全国高一课时练习)一辆汽车在某段路上的行驶路程s关于时间t变化的图像如图,那么图像所
对应的函数模型是( )
A.分段函数 B.二次函数
C.指数函数 D.对数函数
6.(2020·全国高一课时练习)某大型超市为了满足顾客对商品的购物需求,对超市的商品种类做了一定
的调整,结果调整初期利润增长迅速,随着时间的推移,增长速度越来越慢,如果建立恰当的函数模型来
反映该超市调整后利润y与售出商品的数量x的关系,则可选用( )
A.一次函数 B.二次函数
C.指数型函数 D.对数型函数
7.(2020·全国高一课时练习)四人赛跑,假设他们跑过的路程f(x)(其中i∈{1,2,3,4})和时间x(x>1)的函数
i
关系分别是f(x)=x2,f(x)=4x,f(x)=log x,f(x)=2x,如果他们一直跑下去,最终跑在最前面的人具有的
1 2 3 2 4
函数关系是( )
A.f(x)=x2 B.f(x)=4x C.f(x)=log x D.f(x)=2x
1 2 3 2 4
8.(2020·湖北郧阳�高二月考)一种药在病人血液中的量保持 以上才有效,而低于 病人
就有危险.现给某病人注射了这种药 ,如果药在血液中以每小时 的比例衰减,为了充分发
挥药物的利用价值,那么从现在起经过( )小时向病人的血液补充这种药,才能保持疗效.(附:
, ,答案采取四舍五入精确到 )
A.2.3小时 B.3.5小时 C.5.6小时 D.8.8小时
9.(2018·四川高三其他(理))中国高速铁路技术世界领先,高速列车运行时不仅速度比普通列车快而且噪声更小.我们用声强I(单位:W/m2)表示声音在传播途径中每1平方米面积上声能流密度,声强级
L(单位:dB)与声强I的函数关系式为: .若普通列车的声强级是95dB,高速列车的
1
声强级是45dB,则普通列车的声强是高速列车声强的( )
A. 倍 B. 倍 C. 倍 D. 倍
10.(2020·沙坪坝�重庆一中高三月考(理))为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯在公
元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大它的光就越暗.到了
1850年,由于光度计在天体光度测量的应用,英国天文学家普森又提出了亮度的概念,天体的明暗程度可
以用星等或亮度来描述.两颗星的星等与亮度满足 ,其中星等为 的星的亮度
为 .已知“心宿二”的星等是1.00,“天津四”的星等是1.25,则“心宿二”的亮度大约是“天津四”的
( )倍.(当 较小时, )
A.1.27 B.1.26 C.1.23 D.1.22
二、多选题
11.(2019·全国高一课时练习)在某种金属材料的耐高温试验中,温度 随着时间 变化的情况由计算机
记录后显示的图像如图所示给出下列说法,其中正确的是( )
A.前5min温度增加的速度越来越快
B.前5min温度增加的速度越来越慢
C.5min以后温度保持匀速增加
D.5min以后温度保持不变
E.温度随时间的变化情况无法判断
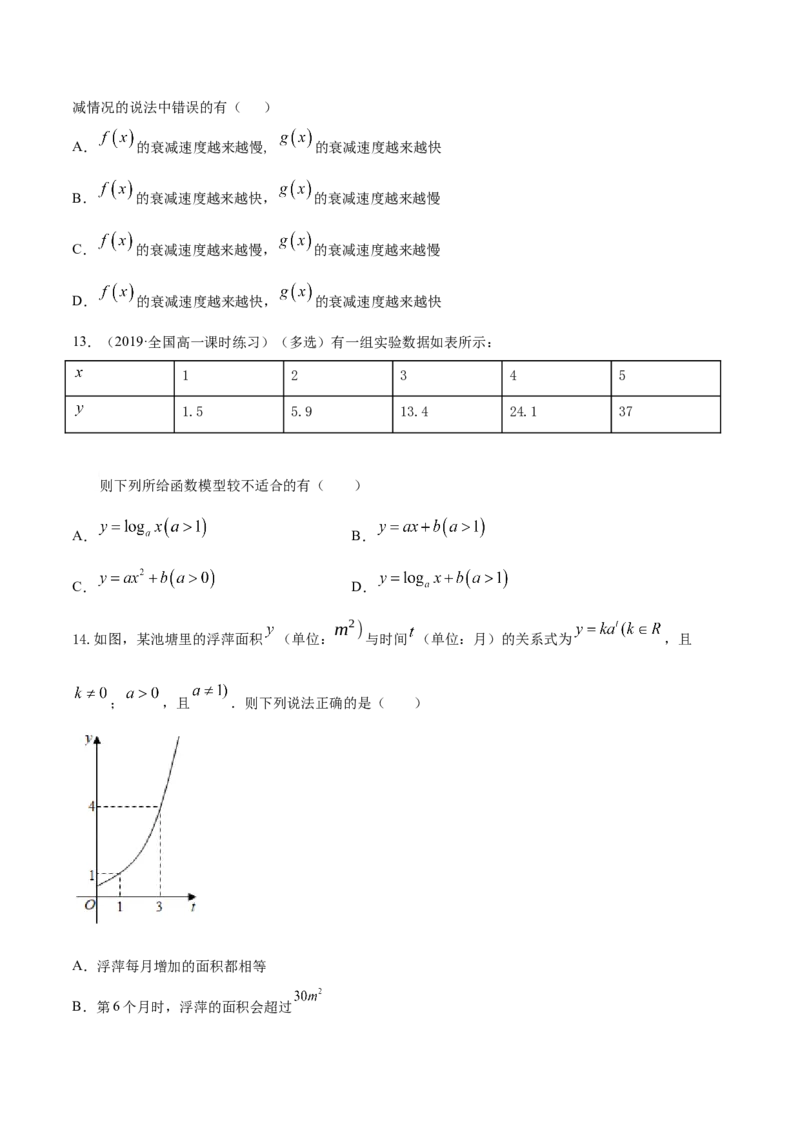
12.(2019·全国高一课时练习)(多选)下面对函数 与 在区间 上的衰减情况的说法中错误的有( )
A. 的衰减速度越来越慢, 的衰减速度越来越快
B. 的衰减速度越来越快, 的衰减速度越来越慢
C. 的衰减速度越来越慢, 的衰减速度越来越慢
D. 的衰减速度越来越快, 的衰减速度越来越快
13.(2019·全国高一课时练习)(多选)有一组实验数据如表所示:
1 2 3 4 5
1.5 5.9 13.4 24.1 37
则下列所给函数模型较不适合的有( )
A. B.
C. D.
m2
)
14.如图,某池塘里的浮萍面积 (单位: 与时间 (单位:月)的关系式为 ,且
; ,且 .则下列说法正确的是( )
A.浮萍每月增加的面积都相等
B.第6个月时,浮萍的面积会超过C.浮萍面积从 蔓延到 只需经过5个月
D.若浮萍面积蔓延到 , , 所经过的时间分别为 , , ,则
三、填空题
15.(2020·全国高一课时练习)下列选项是四种生意预期的收益y关于时间x的函数,从足够长远的角度
看,更为有前途的生意是________.
① ;② ;③ ;④
16.(2020·衡水中学实验学校高三一模(文))某食品的保鲜时间 (单位:小时)与储藏温度 (单位:
满足函数关系 为自然对数的底数, 、 为常数),若该食品在 的保鲜时
间是192小时,在 的保鲜时间是48小时,则该食品在 的保鲜时间是___小时.
17.(2020·全国高三月考(理))2018年5月至2019年春,在阿拉伯半岛和伊朗西南部,沙漠蚂虫迅速
繁衍,呈现几何式的爆发,仅仅几个月,蝗虫数量增长了8000倍,引发了蝗灾,到2020年春季蝗灾已波
及印度和巴基斯坦,假设蝗虫的日增长率为5%,最初有 只,则经过____________天能达到最初的
16000倍(参考数据: , , , ).
四、双空题
18.(2020·浙江高一单元测试)某地西红柿从2月1日起开始上市,通过市场调查,得到西红柿种植成本
(单位:元/( ))与上市时间 (单位:天)的数据如下表:
时间 (单位:天) 60 100 180
种植成本 (单位:元/( )) 116 84 116
根据上表数据,从下列函数中选取一个函数描述西红柿种植成本 与上市时间 的变化关系: ,
, , .利用你选取的函数,计算西红柿种植成本最低时的上市天数是________;最低种植成本是________元/( ).
19.(2019·山东黄岛�高三期中)声强级 (单位: )由公式 给出,其中 为声强
(单位: ).
(1)平时常人交谈时的声强约为 ,则其声强级为______ ;
(2)一般正常人听觉能忍受的最高声强为 ,能听到的最低声强为 ,则正常人听觉的
声强级范围为______ .
20.(2020·全国高三专题练习(理)) 年 月,中国良渚古城遗址获准列入世界遗产名录,标志着
中华五千年文明史得到国际社会认可.良渚古城遗址是人类早期城市文明的范例,实证了中华五千年文明
史.考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳 的
质量 随时间 (单位:年)的衰变规律满足 ( 表示碳 原有的质量),则经过
年后,碳 的质量变为原来的________;经过测定,良渚古城遗址文物样本中碳 的质量是原来的 至
,据此推测良渚古城存在的时期距今约在________年到 年之间.(参考数据:
)
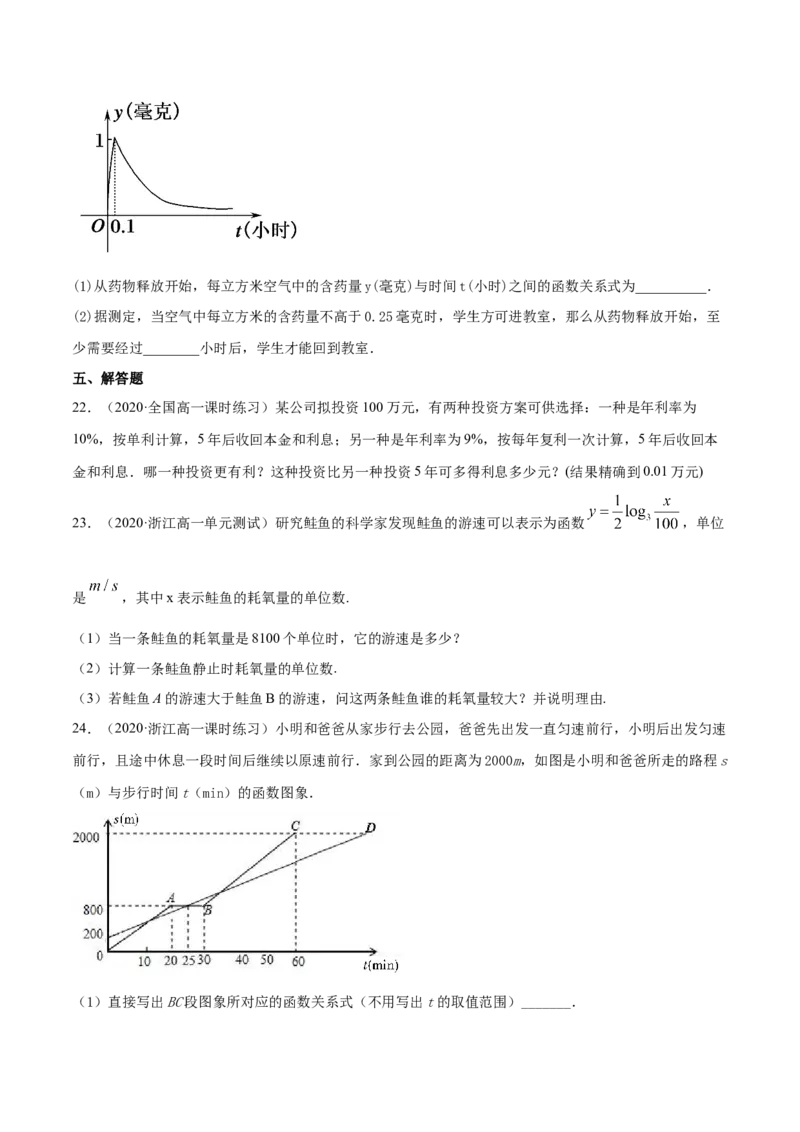
21.(2020·全国高一课时练习)为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程
中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式
y= (a为常数),如图所示,根据图中提供的信息,回答下列问题:(1)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为__________.
(2)据测定,当空气中每立方米的含药量不高于0.25毫克时,学生方可进教室,那么从药物释放开始,至
少需要经过________小时后,学生才能回到教室.
五、解答题
22.(2020·全国高一课时练习)某公司拟投资100万元,有两种投资方案可供选择:一种是年利率为
10%,按单利计算,5年后收回本金和利息;另一种是年利率为9%,按每年复利一次计算,5年后收回本
金和利息.哪一种投资更有利?这种投资比另一种投资5年可多得利息多少元?(结果精确到0.01万元)
23.(2020·浙江高一单元测试)研究鲑鱼的科学家发现鲑鱼的游速可以表示为函数 ,单位
是 ,其中x表示鲑鱼的耗氧量的单位数.
(1)当一条鲑鱼的耗氧量是8100个单位时,它的游速是多少?
(2)计算一条鲑鱼静止时耗氧量的单位数.
(3)若鲑鱼A的游速大于鲑鱼B的游速,问这两条鲑鱼谁的耗氧量较大?并说明理由.
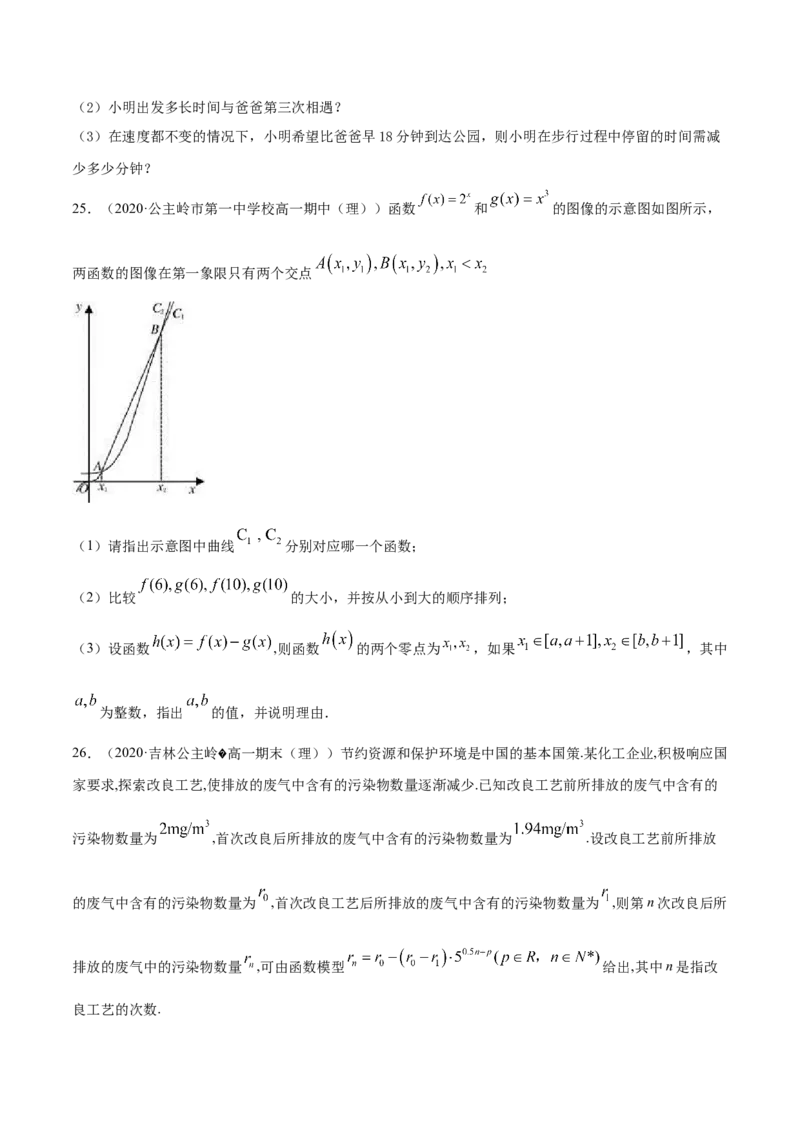
24.(2020·浙江高一课时练习)小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发匀速
前行,且途中休息一段时间后继续以原速前行.家到公园的距离为2000m,如图是小明和爸爸所走的路程s
(m)与步行时间t(min)的函数图象.
(1)直接写出BC段图象所对应的函数关系式(不用写出t的取值范围)_______.(2)小明出发多长时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早18分钟到达公园,则小明在步行过程中停留的时间需减
少多少分钟?
25.(2020·公主岭市第一中学校高一期中(理))函数 和 的图像的示意图如图所示,
两函数的图像在第一象限只有两个交点
(1)请指出示意图中曲线 分别对应哪一个函数;
(2)比较 的大小,并按从小到大的顺序排列;
(3)设函数 ,则函数 的两个零点为 ,如果 ,其中
为整数,指出 的值,并说明理由.
26.(2020·吉林公主岭�高一期末(理))节约资源和保护环境是中国的基本国策.某化工企业,积极响应国
家要求,探索改良工艺,使排放的废气中含有的污染物数量逐渐减少.已知改良工艺前所排放的废气中含有的
污染物数量为 ,首次改良后所排放的废气中含有的污染物数量为 .设改良工艺前所排放
的废气中含有的污染物数量为 ,首次改良工艺后所排放的废气中含有的污染物数量为 ,则第n次改良后所
排放的废气中的污染物数量 ,可由函数模型 给出,其中n是指改
良工艺的次数.(1)试求改良后所排放的废气中含有的污染物数量的函数模型;
(2)依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过 ,试问至少进行多少次
改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.
(参考数据:取 )
27.(2020·山东莱州一中高二月考)某种出口产品的关税税率t,市场价格x(单位:千元)与市场供应
量p(单位:万件)之间近似满足关系式:p ,其中k,b均为常数.当关税税率为75%时,若
市场价格为5千元,则市场供应量均为1万件;若市场价格为7千元,则市场供应量约为2万件.
(1)试确定k、b的值;
(2)市场需求量q(单位:万件)与市场价格x近似满足关系式:q=2﹣x.p=q时,市场价格称为市场平
衡价格.当市场平衡价格不超过4千元时,试确定关税税率的最大值.