文档内容
2.5.1直线与圆的位置关系 -B提高练
一、选择题
1.(2020上海高二课时练习)若直线 与圆 有两个不同的公共点,那么点 与
圆 的位置关系是( ).
A.点在圆外 B.点在圆内 C.点在圆上 D.不能确定
2.(2020湖南衡阳二中高二月考)已知过点P(2,2) 的直线与圆 相切, 且与直线
垂直, 则 ( )
A. B.1 C.2 D.
3.直线x+y+2=0分别与x轴、y轴交于A,B两点,点P在圆(x-2)2+y2=2上,则△ABP面积的取值范围是( )
A.[2,6] B.[4,8] C.[√2,3√2] D.[2√2,3√2]
4.(2020全国高二课时练习)点 在直线 上, , 与圆 分别相切于
A,B两点, O为坐标原点,则四边形PAOB面积的最小值为 ( )
A.24 B.16 C.8 D.4
5.(多选题)(2020·江苏连云港高二期末)瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重
心、垂心位于同一直线上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC,AB=
AC=4,点B(-1,3),点C(4,-2),且其“欧拉线”与圆M: 相切,则下列结论正确
的是( )
A.圆M上点到直线 的最小距离为2
B.圆M上点到直线 的最大距离为3
C.若点(x,y)在圆M上,则 的最小值是D.圆 与圆M有公共点,则a的取值范围是
6.(多选题)(2020江苏省响水中学高二月考)在平面直角坐标系 中,圆 的方程为
.若直线 上存在一点 ,使过 所作的圆的两条切线相互垂直,则实数 的
取可以是( )
A. B. C. D.
二、填空题
7.(2020全国高二课时练习)直线l与圆 相交于A,B两点,若弦AB的
中点为 ,则直线l的方程为____________.
8.(2020·浙江温州高二月考)已知 ,则直线 过定点__________;若直线
与圆 恒有公共点,则半径r的取值范围是__________.
9.(2020·上海高二课时练习)若直线 与圆 相交于 两点,且
(其中 为原点),则 的值为__________.
10.(2020湖北襄阳三中高二月考)如图,正方形ABCD的边长为20米,圆O的半径为1米,圆心是正方形的
中心,点P、Q分别在线段AD、CB上,若线段PQ与圆O有公共点,则称点Q在点P的“盲区”中,已知点P
以1.5米/秒的速度从A出发向D移动,同时,点Q以1米/秒的速度从C出发向B移动,则在点P从A移动到D
的过程中,点Q在点P的盲区中的时长约 秒(精确到0.1).
三、解答题
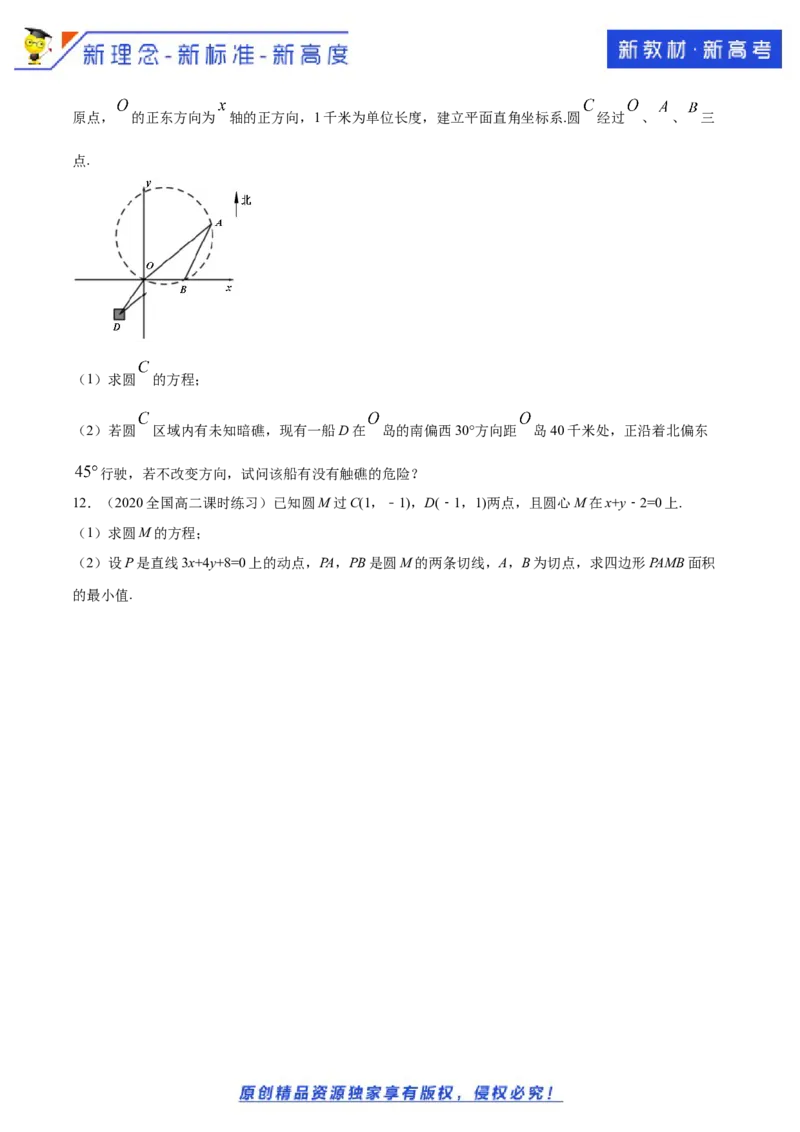
11.(2020·上海市金山中学高二期末)如图,某海面上有 、 、 三个小岛(面积大小忽略不计),
岛在 岛的北偏东 方向距 岛 千米处, 岛在 岛的正东方向距 岛20千米处.以 为坐标原点, 的正东方向为 轴的正方向,1千米为单位长度,建立平面直角坐标系.圆 经过 、 、 三
点.
(1)求圆 的方程;
(2)若圆 区域内有未知暗礁,现有一船D在 岛的南偏西30°方向距 岛40千米处,正沿着北偏东
行驶,若不改变方向,试问该船有没有触礁的危险?
12.(2020全国高二课时练习)已知圆M过C(1,﹣1),D(﹣1,1)两点,且圆心M在x+y﹣2=0上.
(1)求圆M的方程;
(2)设P是直线3x+4y+8=0上的动点,PA,PB是圆M的两条切线,A,B为切点,求四边形PAMB面积
的最小值.