文档内容
3.1.2椭圆的简单几何性质(2) -B提高练
一、选择题
1.(2020·江苏省镇江中学开学考试)设椭圆 的左、右焦点分别为 , ,上
顶点为 ,若 则该椭圆的方程为( )
A. B. C. D.
【答案】A
【解析】因为 ,所以 ,由 可得 ,
所以椭圆方程是: .
2.(2020·安徽省太和中学开学考试)“ ”是“直线 与椭圆 有公共点”的
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
【答案】A
【解析】由 ,得直线 过点 .又点 在椭圆 内部,故
直线 与椭圆 有公共点,而直线 与椭圆 有公共点不一
定 .所以“ ”是“直线 与椭圆 有公共点”的充分不必要条件.故
选:A.
3.(2020·辽宁大连月考)2020年3月9日,我国在西昌卫星发射中心用长征三号运载火箭,成功发
射北斗系统第54颗导航卫星.第54颗导航卫星的运行轨道是以地心为一个焦点的椭圆.设地球半径为 ,若其近地点、远地点离地面的距离大约分别是 , ,则第54颗导航卫星运行轨道(椭
圆)的离心率是( )
A. B. C. D.
【答案】D
【解析】以运行轨道的中心为原点,长轴所在直线为 轴建立平面直角坐标系,
令地心 为椭圆的右焦点,设标准方程为 ( ),
则地心 的坐标为( ,0),其中 .由题意,得 , ,
解得 , ,所以 .
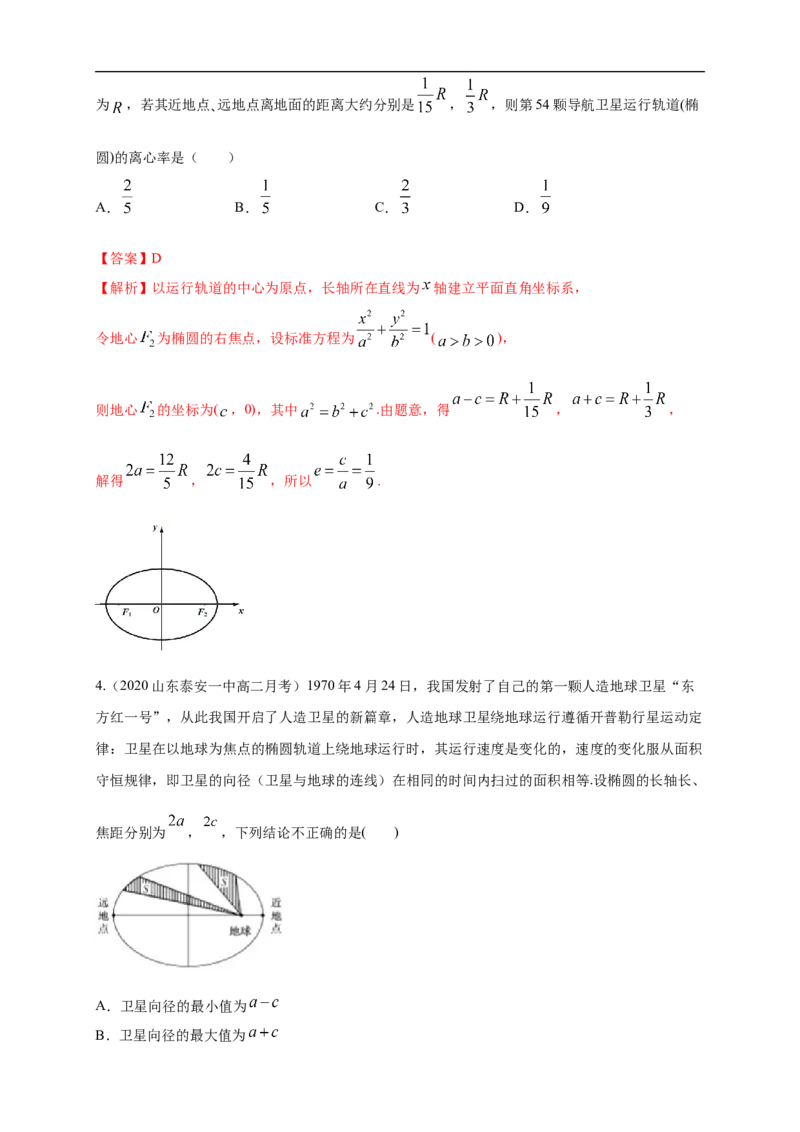
4.(2020山东泰安一中高二月考)1970年4月24日,我国发射了自己的第一颗人造地球卫星“东
方红一号”,从此我国开启了人造卫星的新篇章,人造地球卫星绕地球运行遵循开普勒行星运动定
律:卫星在以地球为焦点的椭圆轨道上绕地球运行时,其运行速度是变化的,速度的变化服从面积
守恒规律,即卫星的向径(卫星与地球的连线)在相同的时间内扫过的面积相等.设椭圆的长轴长、
焦距分别为 , ,下列结论不正确的是( )
A.卫星向径的最小值为
B.卫星向径的最大值为C.卫星向径的最小值与最大值的比值越小,椭圆轨道越扁
D.卫星运行速度在近地点时最小,在远地点时最大
【答案】D
【解析】根据题意:向径为卫星与地球的连线,即椭圆上的点与焦点的连线的距离.
根据椭圆的几何性质有:卫星向径的最小值为 ,卫星向径的最大值为 ,所以A, B正确.
当卫星向径的最小值与最大值的比值越小时,由 ,可得 越大,椭圆越扁,
所以C正确.卫星运行速度在近地点时,其向径最小,由卫星的向径在相同的时间内扫过的面积相等.
则卫星运行速度在近地点时最大,同理在远地点时最小,所以D不正确.故选:D
5.(多选题)设椭圆 的右焦点为F,直线 与椭圆交于A,B两点,
则( )
A. 为定值 B. 的周长的取值范围是
C.当 时, 为直角三角形 D.当 时, 的面积为
【答案】ACD
【解析】设椭圆的左焦点为 ,则 ∴ 为定值,A正确;
的周长为 ,因为 为定值6,∴ 的范围是 ,
∴ 的周长的范围是 ,B错误;将 与椭圆方程联立,可解得 ,
,又∵ ,∴ ,
∴ 为直角三角形,C正确;将 与椭圆方程联立,解得 , ,
∴ ,D正确.故选:ACD6. (多选题)(2020江苏扬州中学月考)已知椭圆 的左、右焦点分别
为 , 且 ,点 在椭圆内部,点 在椭圆上,则以下说法正确的是( )
A. 的最小值为
B.椭圆 的短轴长可能为2
C.椭圆 的离心率的取值范围为
D.若 ,则椭圆 的长轴长为
【答案】ACD
【解析】A. 因为 ,所以 ,所以
,当 ,三点共线时,取等号,故正确;B.若椭圆
的短轴长为2,则 ,所以椭圆方程为 , ,则点 在椭圆外,故
错误;C. 因为点 在椭圆内部,所以 ,又 ,所以 ,所以
,即 ,解得 ,所以 ,
所以 ,所以椭圆 的离心率的取值范围为 ,故正确;D. 若
,则 为线段 的中点,所以 ,所以 ,又 ,即,解得 ,所以 ,所以
椭圆 的长轴长为 ,故正确.故选:ACD
二、填空题
7. (2020·广西南宁高二月考)已知O为坐标原点,点 , 分别为椭圆 的左、
右焦点,A为椭圆C上的一点,且 , 与y轴交于点B,则 ________.
【答案】
【解析】因为 ,所以 的长度是椭圆 通径的一半,即 ,因
为 ,所以 是三角形 的中位线,即 .
8. (2020南昌县莲塘第一中学月考)已知 、 是椭圆 的左,右焦点,
点 为 上一点, 为坐标原点, 为正三角形,则 的离心率为__________.
【答案】
【解析】如图,因为 为正三角形,所以 ,所以 是直角三角形.
因为 , ,所以 ,所以
,所以 ,因为 ,所以
,即 ,所以 .
9.(2020·山东泰安实验中学期末)直线 交椭圆 于 两点,若 ,
则 的值为__________.
【答案】12
【解析】解法一:由椭圆 ,则顶点为 ,而直线 也过 ,
所以 为直线与椭圆的一个交点,设 ,
则 = ,解得: ,
所以 或 (不合,舍去),把 代入椭圆方程得: ,故 .
解法二:由 得 ,所以 ,
又 ,
所以 = ,因为 ,所以 ,故 .
10.(2020·河南南阳中学高二月考)过椭圆 右焦点的直线交于 两点, 为 的中点,且 的斜率为 ,则椭圆 的方程为
__________.
【答案】
【解析】设 ,则 , , ,
由此可得: ,因为 , , ,所
以 .又由题意知, 的右焦点为 ,故 ,因此 ,所以
的方程为: .
三、解答题
11.(2020·贵港市高级中学期中)已知平面内两定点 ,动点 满足
.
(1)求动点 的轨迹 的方程;
(2)若直线 与曲线C交于不同的两点 、 ,求 .
【解析】(1)由椭圆的定义知, 点的轨迹为椭圆,其中 ,所以所求动点
的轨迹 的方程为 .
(2)设 , ,联立直线与椭圆的方程 消 整理得: ,
所以 , ,
.
12.(2020天津实验中学高二月考)已知椭圆 的左焦点为 ,左顶点为 ,
上顶点为 .已知 ( 为原点)
(1)求椭圆的离心率;
(2)设经过点 且斜率为 的直线 与椭圆在 轴上方的交点为 ,圆 同时与 轴和直线 相
切,圆心 在直线 上,且 ,求椭圆的方程.
【解析】(1)由题意可得 , ,设 ,
因为 ,所以 ,
所以椭圆离心率为 ;
(2)由(1)得 , ,
所以椭圆方程可设为 ,直线 ,
设圆心 ,由 ,消去y整理得 即,
所以 或 ,当 时, ;当 时, ;
又 在 轴上方,所以 ,
因为 ,所以 ,
因为 , ,
所以 ,所以 ,所以 ,
由圆 同时与 轴和直线 相切,可得圆 的半径为2,
所以点 到直线 的距离 ,解得 (负值舍去),
所以 , ,所以椭圆方程为 .