文档内容
3.2.2双曲线的简单几何性质 (2)-A基础练
一、选择题
1.(2020·河南太康高二月考)双曲线 的离心率为 ,则其渐近线方程是( )
A. B. C. D.
【答案】D
【解析】双曲线 ,即 ,所以 ,由离心率为 ,所以
,解得 ,所以双曲线 ,则渐近线方程为
,故选:D.
2.(2020·珠海市斗门区第一中学高二月考)直线 与双曲线 的交
点个数是( )
A.1 B.2 C.1或2 D.0
【答案】A
【解析】由题意,双曲线 ,可得其渐近线方程为 ,因为直线
与双曲线的一条渐近线 平行,所以它与双曲线只有1个交点.故选:A.
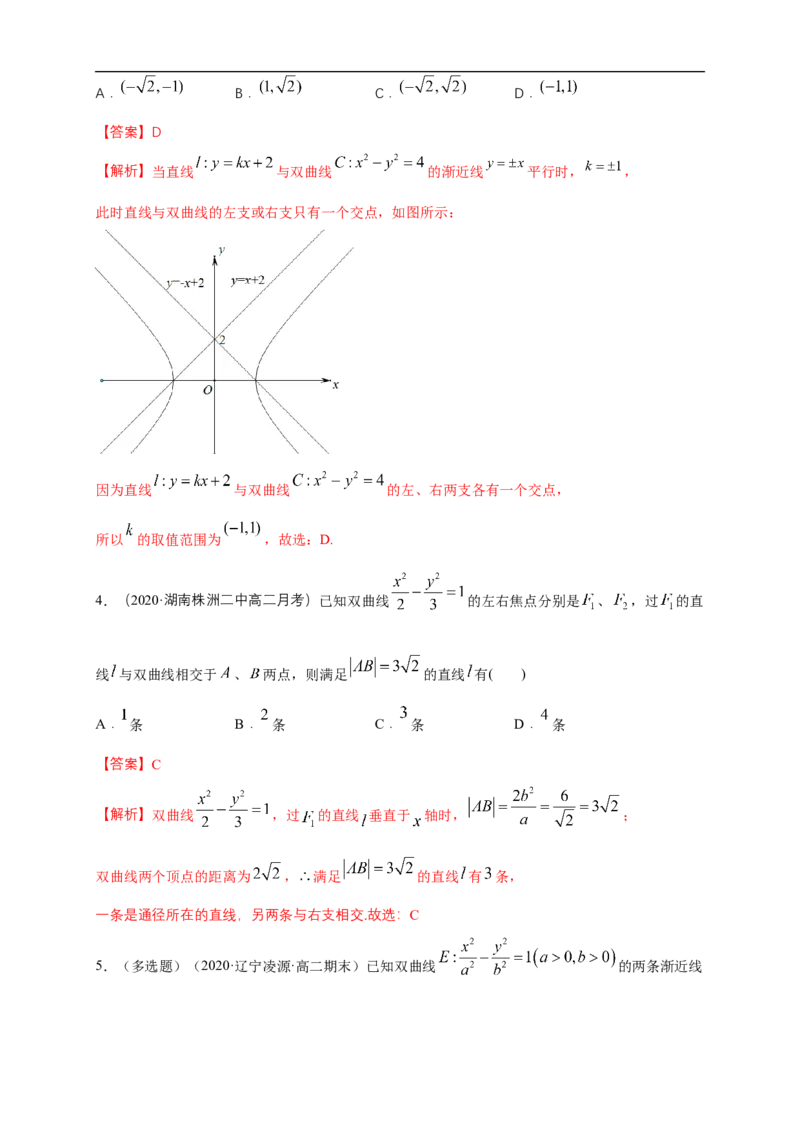
3.(2020·全国高二课时练)若直线 与双曲线 的左、右两支各有一个
交点,则实数 的取值范围是( )A. B. C. D.
【答案】D
【解析】当直线 与双曲线 的渐近线 平行时, ,
此时直线与双曲线的左支或右支只有一个交点,如图所示:
因为直线 与双曲线 的左、右两支各有一个交点,
所以 的取值范围为 ,故选:D.
4.(2020·湖南株洲二中高二月考)已知双曲线 的左右焦点分别是 、 ,过 的直
线 与双曲线相交于 、 两点,则满足 的直线 有( )
A. 条 B. 条 C. 条 D. 条
【答案】C
【解析】双曲线 ,过 的直线 垂直于 轴时, ;
双曲线两个顶点的距离为 , 满足 的直线 有 条,
一条是通径所在的直线,另两条与右支相交.故选:C
5.(多选题)(2020·辽宁凌源·高二期末)已知双曲线 的两条渐近线分别为直线 , ,则下列表述正确的有( )
A. B.
C.双曲线 的离心率为
D.在平面直角坐标系 中,双曲线 的焦点在 轴上
【答案】CD
【解析】因为双曲线 的两条渐近线方程分别为 , ,所以 ,所以 ,
故AB不正确;所以双曲线 的离心率 ;在平面直角坐标系中,双曲线 的焦
点在 轴上.故CD正确 .故选:CD.
6.(多选题)(2020·湖南益阳高二月考)已知双曲线 过点 ,则下列结论正
确的是( )
A.C的焦距为4 B.C的离心率为
C.C的渐近线方程为 D.直线 与C有两个公共点
【答案】AC
【解析】由双曲线 过点 ,可得 ,则双曲线 的标准方程为:
;
所以 ,因为椭圆C的焦距为 ,所以选项A正确;因为椭圆C的离心率为 ,所以选项B不正确;因为椭圆C的渐近线方程为 ,所以
选项C正确;将直线 与双曲线 联立消 可得: ,
,所以直线 与双曲线C没有公共点,所以选项D
不正确;故选:AC.
二、填空题
7.(2020·宁夏石嘴山高二月考)已知双曲线 ( )的离心率为 ,则该双曲线
的渐近线方程为________.
【答案】
【解析】依题意有 ,即 ,解得 ,所以渐近线的方程为
.
8.(2020·安徽宣城高二期末)设双曲线 的左,右焦点分别为 , ,直线 与双
曲线的其中一条渐近线交于点P,则 的面积是________.
【答案】
【解析】由双曲线方程知其渐近线方程为: ,焦点 , ,
则直线 与双曲线的渐近线交于点 , ,不妨设 ,
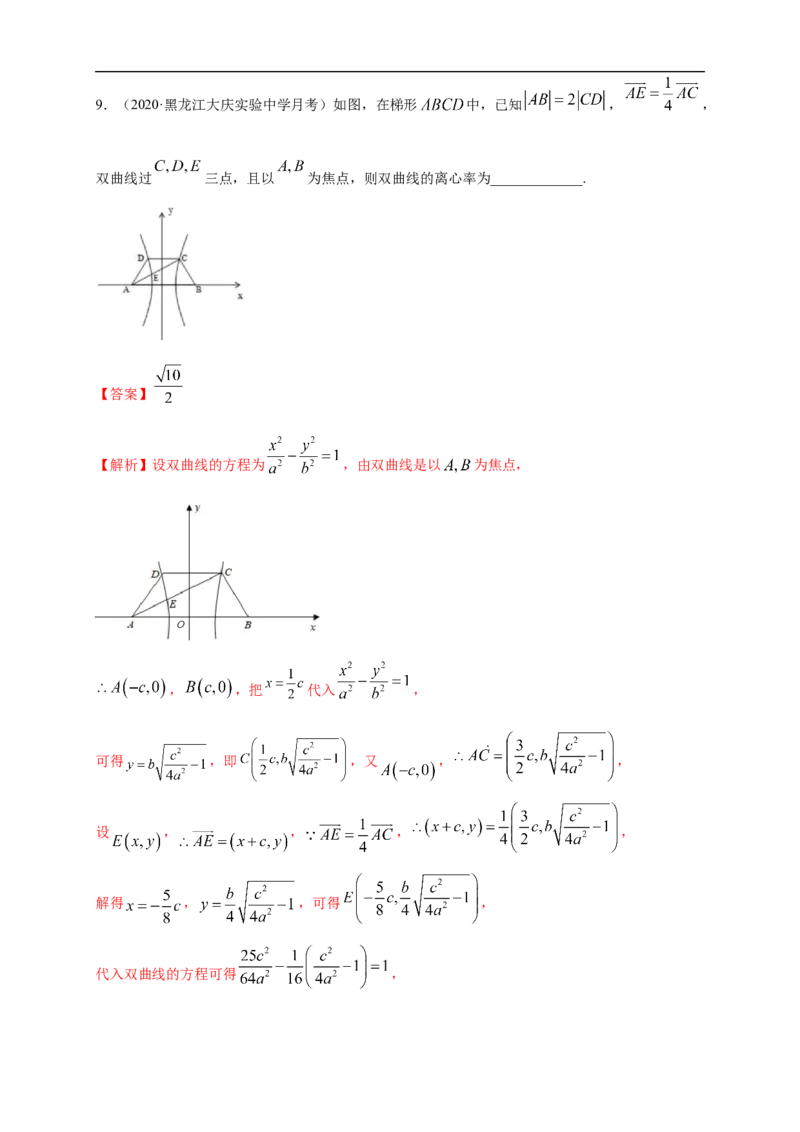
则 .9.(2020·黑龙江大庆实验中学月考)如图,在梯形 中,已知 , ,
双曲线过 三点,且以 为焦点,则双曲线的离心率为_____________.
【答案】
【解析】设双曲线的方程为 ,由双曲线是以 为焦点,
, ,把 代入 ,
可得 ,即 ,又 , ,
设 , , , ,
解得 , ,可得 ,
代入双曲线的方程可得 ,即 ,解得 ,所以 .
10.(2020·西南大学附中高二月考)斜率存在的直线 点 且与双曲线 : 有且只
有一个公共点,则直线 斜率为_____________.
【答案】 或
【解析】由题意,设直线 的方程为 ,代入双曲线方程化简可得 ,
当 即 时, 只有一解,满足直线 与双曲线有且只有一个公共
点;当 时,令 ,解得 ,此时方程有两个相等实数根,
满足直线 与双曲线有且只有一个公共点;所以 或 .
三、解答题
11.(2020·全国高二课时练习)由甲导弹驱逐舰、乙导弹驱逐舰、丙综合补给舰组成的护航编队奔
赴某海域执行护航任务,对商船进行护航。某日,甲舰在乙舰正东方向 处,丙舰在乙舰北偏
西 方向,相距 处,某时刻甲舰发现商船的求救信号,由于乙、丙两舰比甲舰距商船远,因
此 后乙、丙两舰才同时发现这一信号,此信号的传播速度为 ,若甲舰赶赴救援,行进的
方向角应是多少?
【解析】设 分别表示甲舰、乙舰、丙舰和商船.如图所示,以直线 为 轴,线
段 的垂直平分线为 轴建立直角坐标系,则点 在线段 的垂直平分线上,
又易知 ,线段 的中点 ,
∴直线 的方程为 ①
又 ,
∴点 在以 焦点的双曲线的右支上,
∴双曲线方程为 ②
联立①②,得 点坐标为 ,
,因此甲舰行进的方向角为北偏东 .
12.(2020·四川树德中学高二月考)已知双曲线 : 的离心率为 ,点
是双曲线的一个顶点.
(1)求双曲线的方程;
(2)经过双曲线右焦点 作倾斜角为30°的直线,直线与双曲线交于不同的两点 , ,求 .
【解析】(1)由题可得 ,解得 , ,所以双曲线的方程为 ;(2)双曲线 的右焦点为
所以经过双曲线右焦点 且倾斜角为30°的直线的方程为 .
联立 得 .
设 , ,则 , .
所以 .