文档内容
3.3.1 抛物线及其标准方程 -A基础练
一、选择题
1.(2020·江西九江市三中期中)抛物线 的焦点坐标是( )
A.(0,1) B.(1,0) C.(0,2) D.(0, )
【答案】D
【解析】抛物线 的标准方程为 ,故 ,即 ,故焦点坐标是 ,
即 .故选:D.
2.(2020·无锡市第一中学高二期中)在平面内,到直线 与到定点 的距离相等的点
的轨迹是( )
A.抛物线 B.双曲线 C.椭圆 D.直线
【答案】A
【解析】动点 到定点 的距离与到定直线 的距离相等,所以 的轨迹是以点
为焦点,直线 为准线的抛物线,故选: .
3.(2020·南京市天印高级中学高二月考)抛物线 的准线方程为( )
A. B.
C. D.
【答案】C
【解析】因为抛物线 ,所以 ,所以准线方程为 ,故选:C
5
4. (2020·宁夏石嘴山高二月考)已知抛物线C:y2=x的焦点为F,A(x,y)是C上一点,|AF|= x,则x
0 0 0 0
4等于( )
A.4 B.2 C.1 D.8
【答案】C
【解析】如图,F(1
,0
),过A作AA'⊥准线l,∴|AF|=|AA'|,∴5x
0
=x
0
+p=x
0
+1,∴x
0
=1.
4 4 2 4
5.(多选题)(2020·全国高二课时练)对抛物线x2=4y,下列描述不正确的是( )
A.开口向上,焦点为(0,1) B.开口向上,焦点为( 1 )
0,
16
C.开口向右,焦点为(1,0) D.开口向右,焦点为( 1 )
,0
16
【答案】BCD
p
【解析】∵抛物线的标准方程为x2=4y,∴2p=4,p=2,解得 =1,因此抛物线的焦点为(0,1),准线为y=-1,
2
可得该抛物线的开口向上.
6.(多选题)(2020·湖北黄石一中高二期末)经过点 的抛物线的标准方程为( )
A. B. C. D.
【答案】AC
【解析】若抛物线的焦点在x轴上,设抛物线的方程为 ,又因为抛物线经过点
,所以 ,解得 ,所以抛物线的方程为 .若抛物线的焦点在y轴
上,设抛物线的方程为 ,又因为抛物线经过点 ,所以 ,
解得 ,所以抛物线的方程为 .故选:AC.二、填空题
7.若抛物线y2=4x上的点M到焦点的距离为10,则M到y轴的距离是 .
【答案】9
【解析】抛物线y2=4x的焦点F(1,0),准线为x=-1.由M到焦点的距离为10,可知M到准线x=-1的距
离也为10,故M的横坐标满足x +1=10,解得x =9,所以点M到y轴的距离为9.
M M
8.(2020·南京师范大学附中高二月考)若抛物线 的焦点恰好是双曲线
的右焦点,则 .
【答案】 6
【解析】抛物线 的焦点坐标为 , ,双曲线 中, , ,
, 双曲线 的右焦点为 ,则 ,得 .
9.(2020·唐山市第十一中学高二期末)已知点M(1,2)在抛物线C:y2=2px(p>0)上,则点
M到抛物线C焦点的距离是______.
【答案】2
【解析】由点M(1,2)在抛物线C:y2=2px(p>0)上,可得4=2p,p=2, 抛物线C:y2=4x,
焦点坐标F(1,0), 则点M到抛物线C焦点的距离是:1+1=2,
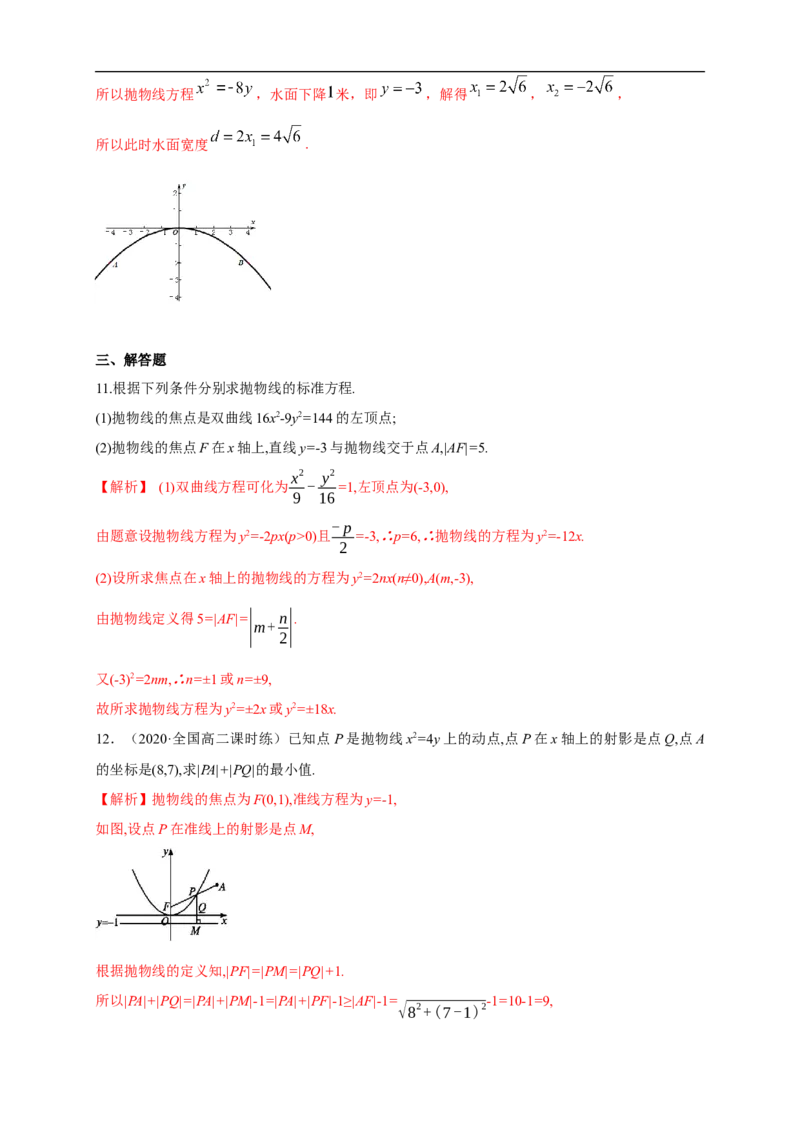
10.(2020·江苏启东中学高二)中国古代桥梁的建筑艺术,有不少是世界桥梁史上的创举,充分显
示了中国劳动人民的非凡智慧.一个抛物线型拱桥,当水面离拱顶2m时,水面宽8m.若水面下降
1m,则水面宽度为______.
【答案】 m
【解析】由题意,以拱桥顶点为原点,建立直角坐标系,设抛物线方程 ,
由题意知,抛物线经过点 和点 ,代入抛物线方程解得, ,所以抛物线方程 ,水面下降 米,即 ,解得 , ,
所以此时水面宽度 .
三、解答题
11.根据下列条件分别求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,|AF|=5.
x2 y2
【解析】 (1)双曲线方程可化为 - =1,左顶点为(-3,0),
9 16
-p
由题意设抛物线方程为y2=-2px(p>0)且 =-3,∴p=6,∴抛物线的方程为y2=-12x.
2
(2)设所求焦点在x轴上的抛物线的方程为y2=2nx(n≠0),A(m,-3),
由抛物线定义得5=|AF|=| n|.
m+
2
又(-3)2=2nm,∴n=±1或n=±9,
故所求抛物线方程为y2=±2x或y2=±18x.
12.(2020·全国高二课时练)已知点P是抛物线x2=4y上的动点,点P在x轴上的射影是点Q,点A
的坐标是(8,7),求|PA|+|PQ|的最小值.
【解析】抛物线的焦点为F(0,1),准线方程为y=-1,
如图,设点P在准线上的射影是点M,
根据抛物线的定义知,|PF|=|PM|=|PQ|+1.
所以|PA|+|PQ|=|PA|+|PM|-1=|PA|+|PF|-1≥|AF|-1= -1=10-1=9,
√82+(7-1)2当且仅当A,P,F三点共线时,等号成立.
故|PA|+|PQ|的最小值为9.