文档内容
3.3.2 抛物线的简单几何性质(2) -B提高练
一、选择题
1.(2020·江西宜春高二期中)已知点A ,抛物线C: 的焦点F.射线FA与抛物线
C相交于点M,与其准线相交于点N,则 =( )
A. B. C. D.
2.(2020·辽宁大连高二月考)已知点P是抛物线 上的一个动点,则点P到点A(0,2)
的距离与P到该抛物线准线的距离之和的最小值为( )
A. B. C. D.
3.已知拋物线y2=8x的焦点为F,过点F的直线与该抛物线交于A,B两点,且16≤|AB|≤24,O为坐标原点,
1 1
+
记直线OA,OB的斜率分别为k,k,则 的取值范围是( )
1 2 k k
1 2
A.[-2,-√2]∪[√2,2] B.[-√2,-1]∪[1,√2] C.[-2,-1]∪[1,2] D.[-√2,√2]
4.(2020·河南洛阳高二月考)已知抛物线y2=16x的焦点为F,过点F作直线l交抛物线于M,N两点,
|NF| 4
则 - 的最小值为( )
9 |MF|
2 2 1 1
A. B.- C.- D.
3 3 3 3
5.(多选题)(2020·江苏如皋高二月考)已知抛物线 的焦点为 , ,
是抛物线上两点,则下列结论正确的是( )
A.点 的坐标为
B.若 , , 三点共线,则
C.若直线 与 的斜率之积为 ,则直线 过点D.若 ,则 的中点到 轴距离的最小值为2
6. (多选题)已知抛物线C:y2=4x的焦点为F,准线为l,过点F的直线与抛物线交于P(x,y),Q(x,y)两
1 1 2 2
点,点P在l上的射影为P,则下列结论中正确的是( )
1
A.若x+x =6,则|PQ|=8
1 2
B.以PQ为直径的圆与准线l相切
C.设M(0,1),则|PM|+|PP |≥ √2
1
D.过点M(0,1)与抛物线C有且只有一个公共点的直线至多有2条
二、填空题
7.(2020·博兴第三中学高二月考)以抛物线 的焦点为圆心,且与抛物线的准线相切的圆
的方程为______________.
8.已知M,N是过抛物线C:y2=2px(p>0)的焦点F的直线l与抛物线C的交点,O是坐标原点,且满足
=3 ,S = |MN|,则p的值为 .
⃗MF ⃗FN
△OMN
√3
9.(2020·华南师大附中高二月考)已知抛物线 在第一象限内的一点 到抛
物线焦点F的距离为4,若P为抛物线准线上任意一点,则当 的周长最小时,点P到直线
的距离为______.
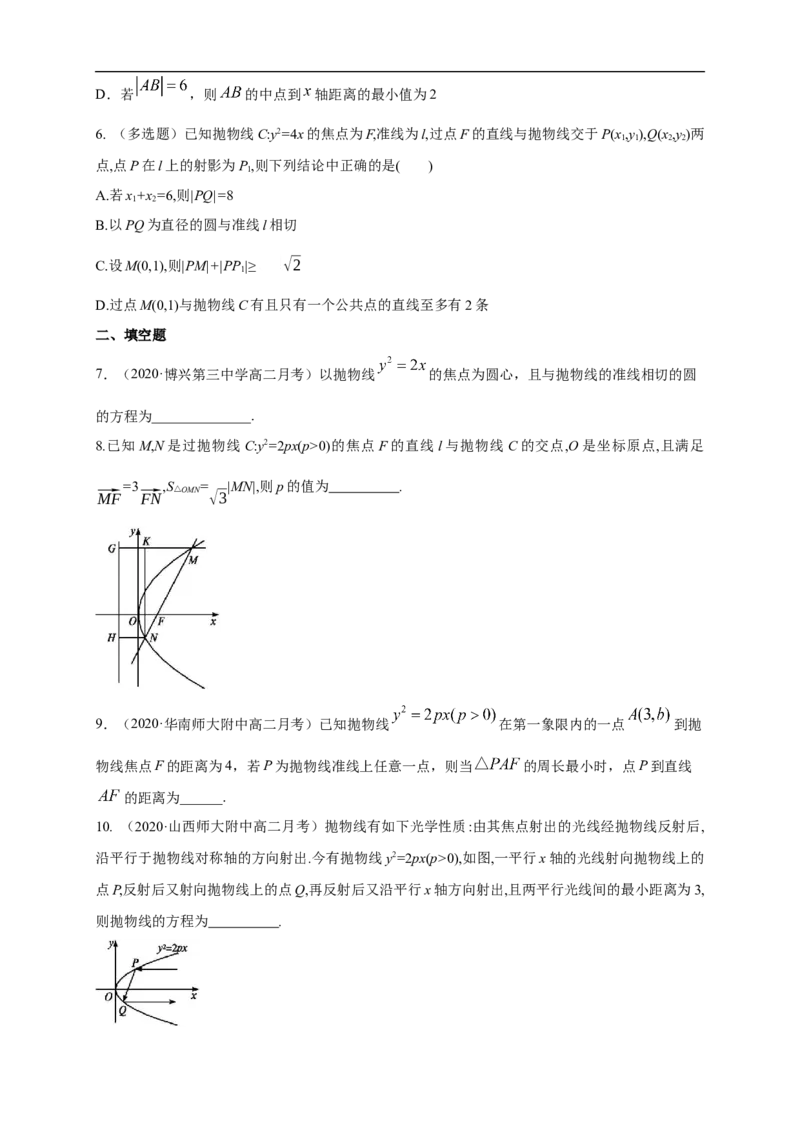
10. (2020·山西师大附中高二月考)抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,
沿平行于抛物线对称轴的方向射出.今有抛物线y2=2px(p>0),如图,一平行x轴的光线射向抛物线上的
点P,反射后又射向抛物线上的点Q,再反射后又沿平行x轴方向射出,且两平行光线间的最小距离为3,
则抛物线的方程为 .三、解答题
11. (2020·利川市第五中学高二期中)已知动点 在抛物线 上,过点 作 轴的垂线,
垂足为 ,动点 满足 .
(1)求动点 的轨迹 的方程;
(2)点 ,过点 且斜率为 的直线交轨迹 于 两点,设直线 的斜率
分别为 ,求 的值.
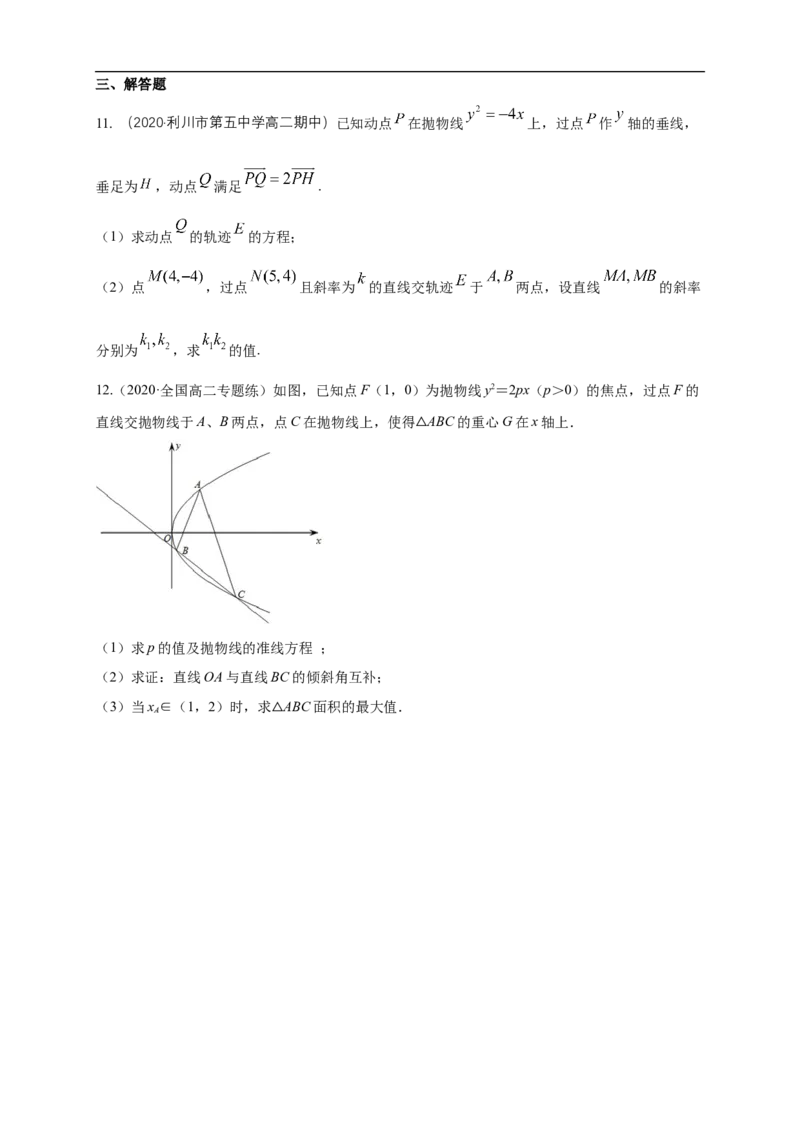
12.(2020·全国高二专题练)如图,已知点F(1,0)为抛物线y2=2px(p>0)的焦点,过点F的
直线交抛物线于A、B两点,点C在抛物线上,使得 ABC的重心G在x轴上.
△
(1)求p的值及抛物线的准线方程 ;
(2)求证:直线OA与直线BC的倾斜角互补;
(3)当x ∈(1,2)时,求 ABC面积的最大值.
A
△