文档内容
格致课堂
8.4.2 空间点、直线、平面之间的位置关系
(用时45分钟)
【选题明细表】
知识点、方法 题号
空间中直线之间的位置关系 1,2,5,8
直线与平面之间的位置关系 3,6,7,9
平面与平面之间的位置关系 4,10,11,12
基础巩固
1.一条直线与两条平行线中的一条成为异面直线,则它与另一条( )
A.相交 B.异面 C.相交或异面 D.平行
【答案】C
【解析】一条直线与两条平行线中的一条异面,则它与另一条可能相交,也可能异面.故选C.
2.已知异面直线a,b分别在平面α,β内,且α∩β=c,那么直线c一定( )
A.与a,b都相交
B.只能与a,b中的一条相交
C.至少与a,b中的一条相交
D.与a,b都平行
【答案】C
【解析】如图,a′与b异面,但a′∥c,故A错;a与b异面,且都与c相交,故B错;若a∥c,b∥c,则a∥b,与a,b异面
矛盾,故D错.
3.下列命题中正确的个数是( )
①若直线l上有无数个点不在平面α内,则l∥α ②若直线l与平面α平行,则l与平面α内的任意一条直线平
行 ③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行 ④若直线l与平面α平
行,则l与平面α内的任意一条直线都没有公共点
A.0 B.1C.2 D.3
【答案】B
【解析】对于①,当直线l与α相交时,直线l上有无数个点不在平面α内,故①不正确;对于②,直线l与平面α格致课堂
平行时,l与平面α内的直线平行或异面,故②不正确:对于③,当两条平行直线中的一条与一个平面平行时,另
一条与这个平面可能平行,也有可能在这个平面内,故③不正确;对于④,由线面平行的定义可知④正确.
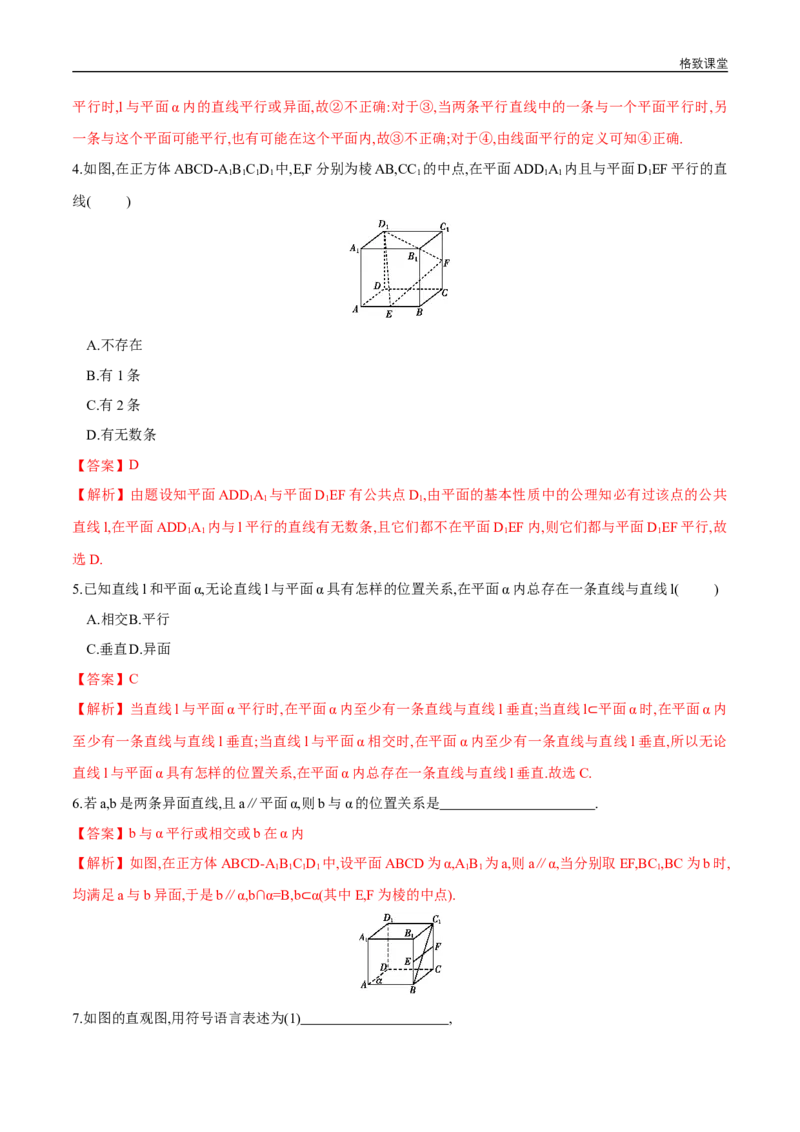
4.如图,在正方体ABCD-A B C D 中,E,F分别为棱AB,CC 的中点,在平面ADDA 内且与平面DEF平行的直
1 1 1 1 1 1 1 1
线( )
A.不存在
B.有1条
C.有2条
D.有无数条
【答案】D
【解析】由题设知平面ADDA 与平面DEF有公共点D,由平面的基本性质中的公理知必有过该点的公共
1 1 1 1
直线l,在平面ADDA 内与l平行的直线有无数条,且它们都不在平面DEF内,则它们都与平面DEF平行,故
1 1 1 1
选D.
5.已知直线l和平面α,无论直线l与平面α具有怎样的位置关系,在平面α内总存在一条直线与直线l( )
A.相交B.平行
C.垂直D.异面
【答案】C
【解析】当直线l与平面α平行时,在平面α内至少有一条直线与直线l垂直;当直线l 平面α时,在平面α内
至少有一条直线与直线l垂直;当直线l与平面α相交时,在平面α内至少有一条直线与⊂直线l垂直,所以无论
直线l与平面α具有怎样的位置关系,在平面α内总存在一条直线与直线l垂直.故选C.
6.若a,b是两条异面直线,且a∥平面α,则b与α的位置关系是 .
【答案】b与α平行或相交或b在α内
【解析】如图,在正方体ABCD-A B C D 中,设平面ABCD为α,A B 为a,则a∥α,当分别取EF,BC ,BC为b时,
1 1 1 1 1 1 1
均满足a与b异面,于是b∥α,b∩α=B,b α(其中E,F为棱的中点).
⊂
7.如图的直观图,用符号语言表述为(1) ,格致课堂
(2) .
【答案】(1)a∩b=P,a∥平面M,b∩平面M=A;(2)平面M∩平面N=l,a∩平面N=A,a∥平面M
【解析】(1)a∩b=P,a∥平面M,b∩平面M=A(2)平面M∩平面N=l,a∩平面N=A,a∥平面M
8.如图,正方体ABCD AB C D 中,M,N分别是AB ,B C 的中点,问
1 1 1 1 1 1 1 1
(1)AM和CN是否是异面直线?
(2)D B和CC 是否是异面直线?说明理由.
1 1
【答案】(1) 不是异面直线;(2)是异面直线,证明见解析.
【解析】由于M,N分别是AB 和B C 的中点,可证明MN∥AC,因此AM与CN不是异面直线.
1 1 1 1
由空间图形可感知DB和CC 为异面直线的可能性较大,判断的方法可用反证法.
1 1
(1)不是异面直线.理由:
因为M,N分别是AB ,B C 的中点,
1 1 1 1
所以MN∥AC .
1 1
又因为AA C C,
1 1
所以AACC 为平行四边形.
1 1
所以AC ∥AC,得到MN∥AC,
1 1
所以A,M,N,C在同一个平面内,
故AM和CN不是异面直线.
(2)是异面直线,证明如下:
假设DB与CC 在同一个平面CC DD内,则
1 1 1 1
B∈平面CC DD,C∈平面CC DD.
1 1 1 1
所以BC 平面CC DD,
1 1
这与AB⊂CD AB C D 是正方体相矛盾.
1 1 1 1
所以假设不成立,格致课堂
故DB与CC 是异面直线.
1 1
能力提升
9.若平面α∥β,直线a α,点B∈β,则在β内过点B的所有直线中( )
A.不一定存在与a平⊂行的直线
B.只有两条直线与a平行
C.存在无数条直线与a平行
D.存在唯一一条与a平行的直线
【答案】D
【解析】因为α∥β,B∈β,所以B α.
因为a α,所以B,a可确定平面γ且∉ γ∩α=a,
设γ与⊂β交过点B的直线为b,则a∥b.
因为a,B在同一平面γ内.
所以b唯一,即存在唯一一条与a平行的直线.
10.已知下列说法:
①若两个平面α∥β,a α,b β,则a∥b;
②若两个平面α∥β,a⊂α,b⊂β,则a与b是异面直线;
③若两个平面α∥β,a⊂α,b⊂β,则a与b一定不相交;
④若两个平面α∥β,a⊂α,b⊂β,则a与b平行或异面;
⑤若两个平面α∩β=b⊂,a α⊂,则a与β一定相交.
其中正确的序号是 ⊂ .(将你认为正确的序号都填上)
【答案】③④
【解析】①错.a与b也可能异面.
②错.a与b也可能平行.
③对.因为α∥β,
所以α与β无公共点.
又因为a α,b β,
所以a与⊂b无⊂公共点.
④对.由③知a与b无公共点,那么a∥b或a与b异面.
⑤错.a与β也可能平行.
11.如图,平面α,β,γ满足α∥β,α∩γ=a,β∩γ=b,判断a与b,a与β的关系并证明你的结论.格致课堂
【答案】a,b无公共点, a∥β,证明见解析.
【解析】a∥b,a∥β,理由:
由α∩γ=a知a α且a γ,
由β∩γ=b知b⊂β且b⊂γ,
因为α∥β,a α⊂,b β, ⊂
所以a,b无公⊂共点⊂.
又因为a γ,且b γ,所以a∥b.
因为α∥⊂β,所以α⊂与β无公共点,
又a α,所以a与β无公共点,所以a∥β.
⊂ 素养达成
12.如图所示,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,且A l,B l,C l,直线AB与l不平行,那么平面ABC与
平面β的交线与l有什么关系?证明你的结论. ∉ ∉ ∉
【答案】平面ABC与β的交线与l相交,证明见解析.
【解析】平面ABC与β的交线与l相交.
证明:因为AB与l不平行,且AB α,l α,
所以AB与l一定相交,设AB∩l=⊂P,则⊂P∈AB,P∈l.
又因为AB 平面ABC,l β,所以P∈平面ABC,P∈β.
所以点P是⊂平面ABC与⊂β的一个公共点,
而点C也是平面ABC与β的一个公共点,且P,C是不同的两点,所以直线PC就是平面ABC与β的交线.
即平面ABC∩β=PC,而PC∩l=P,
所以平面ABC与β的交线与l相交.