文档内容
格致课堂
8.5.1 直线与直线平行
(用时45分钟)
【选题明细表】
知识点、方法 题号
基本事实4及其应用 1,2,4,5,10
等角定理及其应用 3,6,7,8
综合问题 9,11,12
基础巩固
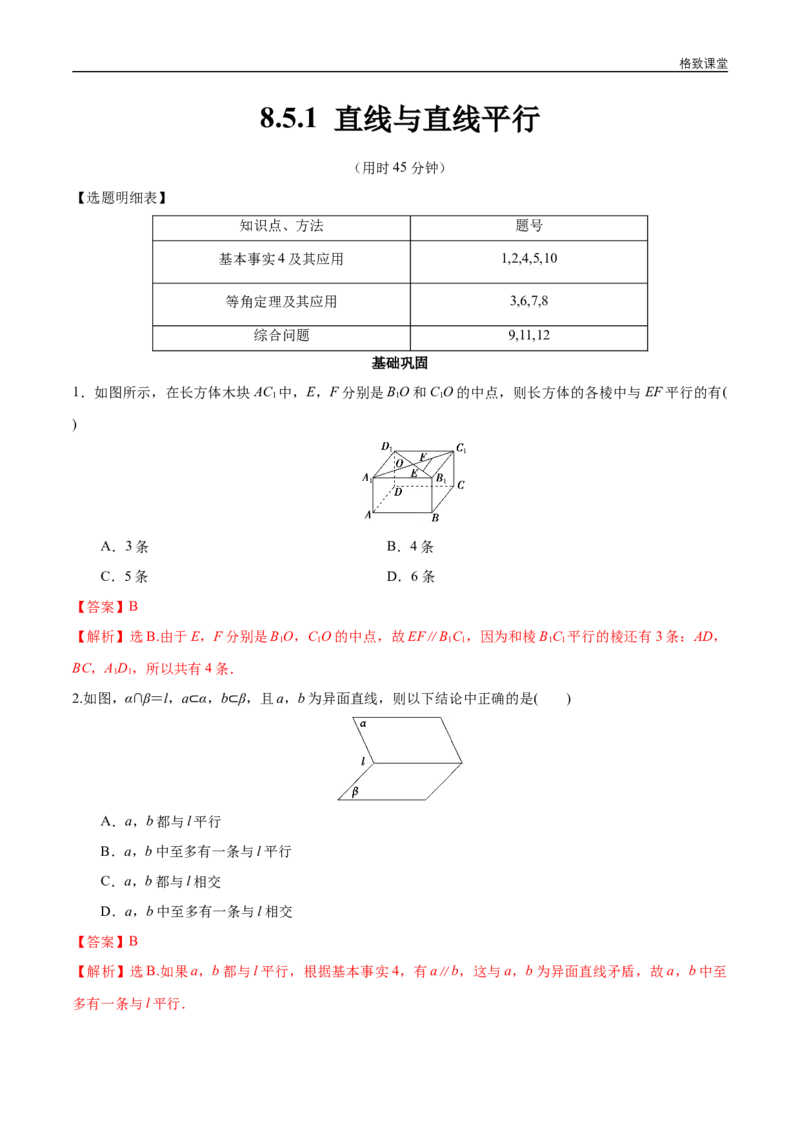
1.如图所示,在长方体木块AC 中,E,F分别是BO和C O的中点,则长方体的各棱中与EF平行的有(
1 1 1
)
A.3条 B.4条
C.5条 D.6条
【答案】B
【解析】选B.由于E,F分别是BO,C O的中点,故EF∥BC ,因为和棱BC 平行的棱还有3条:AD,
1 1 1 1 1 1
BC,AD,所以共有4条.
1 1
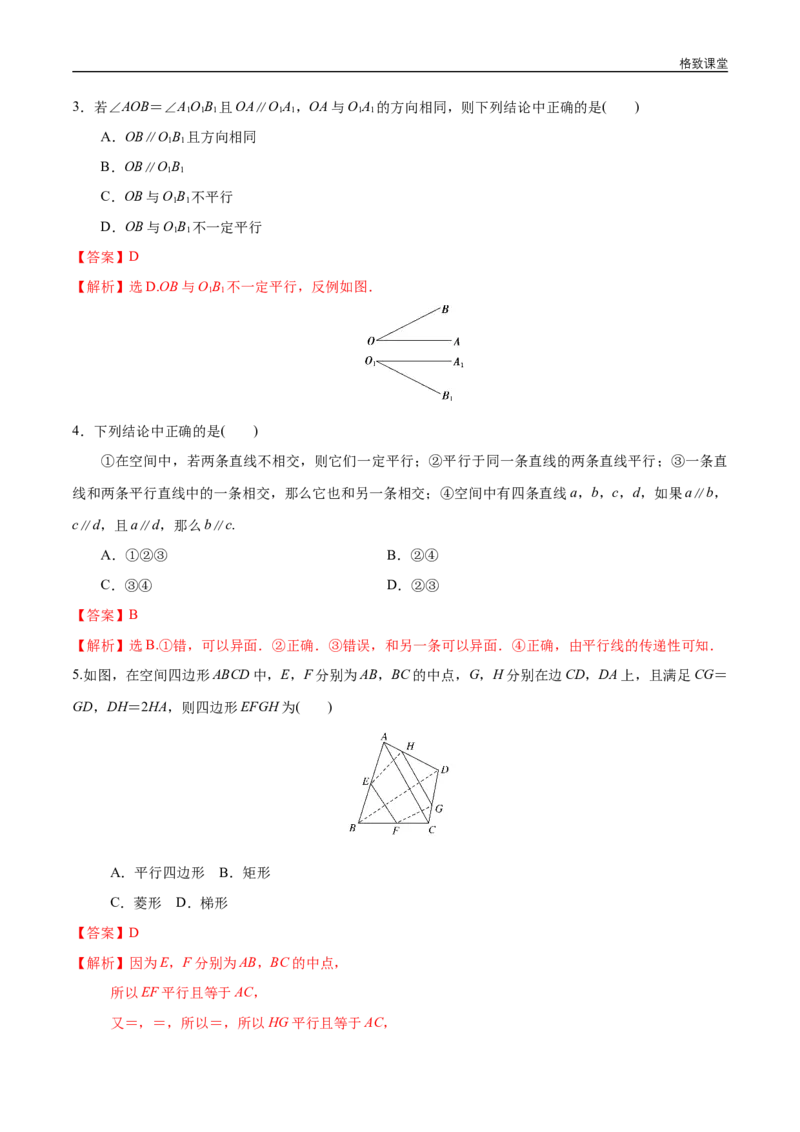
2.如图,α∩β=l,a α,b β,且a,b为异面直线,则以下结论中正确的是( )
⊂ ⊂
A.a,b都与l平行
B.a,b中至多有一条与l平行
C.a,b都与l相交
D.a,b中至多有一条与l相交
【答案】B
【解析】选B.如果a,b都与l平行,根据基本事实4,有a∥b,这与a,b为异面直线矛盾,故a,b中至
多有一条与l平行.格致课堂
3.若∠AOB=∠AOB 且OA∥OA,OA与OA 的方向相同,则下列结论中正确的是( )
1 1 1 1 1 1 1
A.OB∥OB 且方向相同
1 1
B.OB∥OB
1 1
C.OB与OB 不平行
1 1
D.OB与OB 不一定平行
1 1
【答案】D
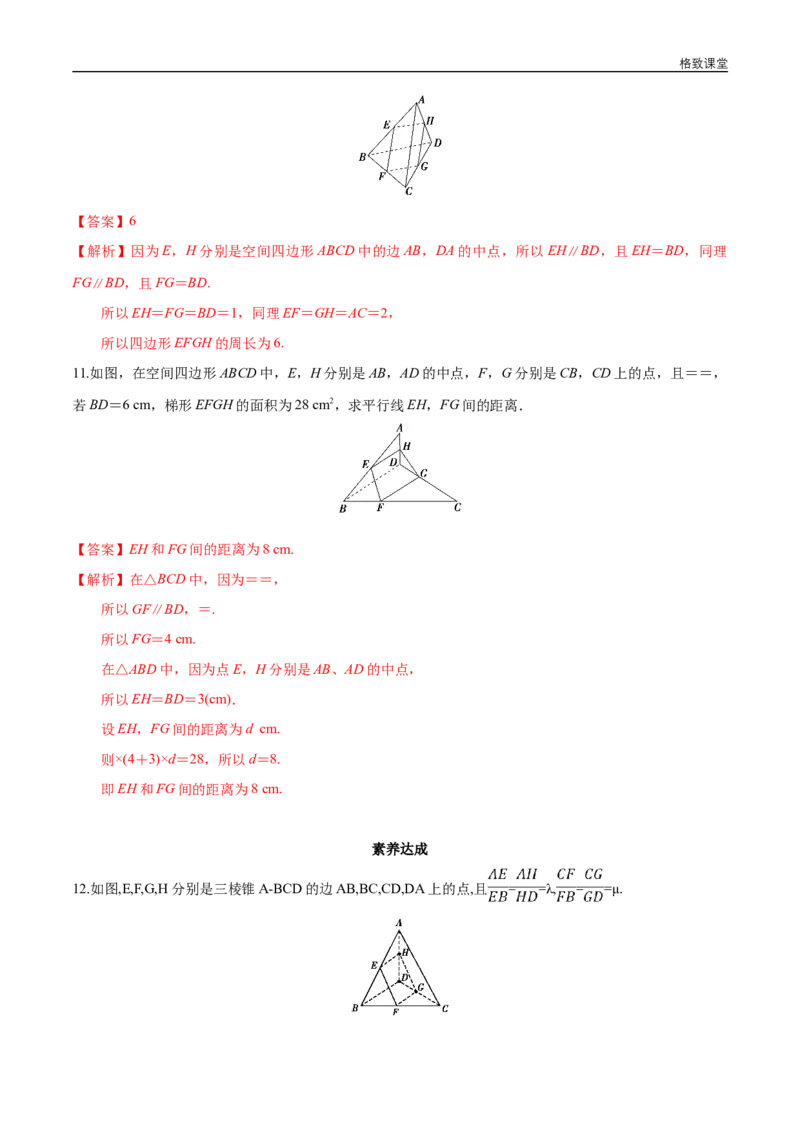
【解析】选D.OB与OB 不一定平行,反例如图.
1 1
4.下列结论中正确的是( )
①在空间中,若两条直线不相交,则它们一定平行;②平行于同一条直线的两条直线平行;③一条直
线和两条平行直线中的一条相交,那么它也和另一条相交;④空间中有四条直线a,b,c,d,如果a∥b,
c∥d,且a∥d,那么b∥c.
A.①②③ B.②④
C.③④ D.②③
【答案】B
【解析】选B.①错,可以异面.②正确.③错误,和另一条可以异面.④正确,由平行线的传递性可知.
5.如图,在空间四边形ABCD中,E,F分别为AB,BC的中点,G,H分别在边CD,DA上,且满足CG=
GD,DH=2HA,则四边形EFGH为( )
A.平行四边形 B.矩形
C.菱形 D.梯形
【答案】D
【解析】因为E,F分别为AB,BC的中点,
所以EF平行且等于AC,
又=,=,所以=,所以HG平行且等于AC,格致课堂
所以EF∥HG且EF≠HG,
所以四边形EFGH为梯形.
6.空间中有两个角α,β,且角α、β的两边分别平行.若α=60°,则β=________.
【答案】60°或120°
【解析】因为α与β两边对应平行,但方向不确定,
所以α与β相等或互补.
答案:60°或120°
7.如图,在正方体ABCDABC D 中,BD和BD 分别是正方形ABCD和ABC D 的对角线,
1 1 1 1 1 1 1 1 1 1
(1)∠DBC的两边与________的两边分别平行且方向相同;
(2)∠DBC的两边与________的两边分别平行且方向相反.
【答案】(1)∠DBC (2)∠BDA
1 1 1 1 1 1
【解析】(1)因为BD∥BD,BC ∥BC且方向相同,所以∠DBC的两边与∠DBC 的两边分别平行且方向
1 1 1 1 1 1 1
相同.
(2)BD∥BD,DA∥BC且方向相反,所以∠DBC的两边与∠BDA 的两边分别平行且方向相反.
1 1 1 1 1 1 1
8.如图,已知在棱长为a的正方体ABCDABC D 中,M,N分别是棱CD,AD的中点.
1 1 1 1
求证:(1)四边形MNA C 是梯形;
1 1
(2)∠DNM=∠DAC .
1 1 1
【答案】证明见解析
【解析】(1)如图,连接AC,因为在△ACD中,M,N分别是CD,AD的中点,所以MN是△ACD的中位
线,格致课堂
所以MN∥AC,MN=AC.
由正方体的性质得:
AC∥AC ,AC=AC .
1 1 1 1
所以MN∥AC ,且MN=AC ,即MN≠AC ,
1 1 1 1 1 1
所以四边形MNA C 是梯形.
1 1
(2)由(1)可知MN∥AC .
1 1
又因为ND∥AD,所以∠DNM与∠DAC 相等或互补.
1 1 1 1 1
而∠DNM与∠DAC 均为锐角,
1 1 1
所以∠DNM=∠DAC .
1 1 1
能力提升
9.如图所示,在四面体ABCD中,M,N,P,Q,E分别是AB,BC,CD,AD,AC的中点,则下列说法
不正确的是( )
A.M,N,P,Q四点共面
B.∠QME=∠CBD
C.△BCD∽△MEQ
D.四边形MNPQ为矩形
【答案】D
【解析】选D.由条件易得MQ∥BD,ME∥BC,QE∥CD,NP∥BD,所以MQ∥NP.对于A,由MQ∥NP,
得M,N,P,Q四点共面,故A正确;对于B,根据定理,得∠QME=∠CBD,故B正确;对于C,由定
理知∠QME=∠CBD,∠MEQ=∠BCD,则△BCD∽△MEQ,故C正确;对于D,没有充分理由推证四
边形MNPQ为矩形,故D不正确.
10.如图所示,E,F,G,H分别是空间四边形ABCD各边AB,BC,CD,DA的中点,若BD=2,AC=
4,则四边形EFGH的周长为________.格致课堂
【答案】6
【解析】因为E,H分别是空间四边形ABCD中的边AB,DA的中点,所以EH∥BD,且EH=BD,同理
FG∥BD,且FG=BD.
所以EH=FG=BD=1,同理EF=GH=AC=2,
所以四边形EFGH的周长为6.
11.如图,在空间四边形ABCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD上的点,且==,
若BD=6 cm,梯形EFGH的面积为28 cm2,求平行线EH,FG间的距离.
【答案】EH和FG间的距离为8 cm.
【解析】在△BCD中,因为==,
所以GF∥BD,=.
所以FG=4 cm.
在△ABD中,因为点E,H分别是AB、AD的中点,
所以EH=BD=3(cm).
设EH,FG间的距离为d cm.
则×(4+3)×d=28,所以d=8.
即EH和FG间的距离为8 cm.
素养达成
12.如图,E,F,G,H分别是三棱锥A-BCD的边AB,BC,CD,DA上的点,且 = =λ, = =μ.格致课堂
(1)若λ=μ,判断四边形EFGH的形状;
(2)若λ≠μ,判断四边形EFGH的形状;
(3)若λ=μ= ,且EG⊥HF,求 的值.
【答案】(1)λ=μ时,四边形EFGH为平行四边形.
(2)λ≠μ时,四边形EFGH为梯形.
(3) = .
【解析】(1)因为 = =λ,
所以EH∥BD,且EH= BD. ①
又因为 = =μ.
所以FG∥BD,且FG= BD. ②
又λ=μ,所以EHFG(公理4).
因此λ=μ时,四边形EFGH为平行四边形.
(2)若λ≠μ,由①②,知EH∥FG,但EH≠FG,
因此λ≠μ时,四边形EFGH为梯形.
(3)因为λ=μ,
所以四边形EFGH为平行四边形.
又因为EG⊥HF,
所以四边形EFGH为菱形.
所以FG=HG.
所以AC=(λ+1)HG= HG= FG,
又BD= FG=3FG,
所以 = .