文档内容
宣城市 2023—2024学年度第二学期期末调研测试
高一数学参考答案
一、选择题:
题 号 1 2 3 4 5 6 7 8
答 案 C D B A A C B D
二、多选题:
题 号 9 10 11
答 案 AC BC ACD
三、填空题:
2槡21 4槡3
1260 13 14
7 3
四、解答题:
2π 槡3
15(1)因为c=2bcosB,则由正弦定理可得sinC=2sinBcosB,所以sin2B=sin = ,
3 2
2π ( π) ( 2π)
又C= ,所以B∈ 0, ,2B∈ 0, ,
3 3 3
π π
故2B= ,解得B= ;……………………………………………………………… 5分
3 6
π
(2)由(1)可得A= ,即a=b,
6
则S =
1
absinC=
1
a2×
槡3
=
3槡3
,解得a=槡3,……………………………… 8分
△ABC 2 2 2 4
则由余弦定理可得BC边上的中线AD长度为:
AD=槡b2+
(a)2
-2×b×
a
×cos
2π
=槡3+
3
+槡3×
槡3
=
槡21
…………… 13分
2 2 3 4 2 2
(其它解法可根据情况适当给分)
16(1)因为|a→|=2,|b→|=3,(a→ +b→)·b→ =8,
所以(a→ +b→)·b→ =a→·b→ +b→2=a→·b→ +9=8,a→·b→ =-1,
则 a→ +b→ =槡(a→ +b→)2=槡a→2+2a→·b→ +b→2=槡4-2+9=槡11…………… 5分
(2)因为ka→ -2b→与a→ +2b→垂直,
所以(ka→ -2b→)·(a→ +2b→)=ka→2+(2k-2)·a→·b→ -4b→2=4k-(2k-2)-36=
2k-34=0,解得k=17 …………………………………………………………… 10分
(3)因为ka→ -b→与4a→ -kb→反向,
所以存在λ<0,使得ka→ -b→ =λ(4a→ -kb→)=4λa→ -λkb→,
宣城市高一数学参考答案第1页(共3页)
{#{QQABSYCEggggAIJAAQgCUQFYCgOQkBEACQgOhFAMoAAAAAFABAA=}#}{k=-2 {k=2
{k=4λ
因为a→,b→不共线,所以 ,解得 1或 1(舍去),
-1=-λk λ=- λ=
2 2
所以k=-2 ……………………………………………………………………… 15分
17(1)由题可知PA⊥PE,PE=DE=1,BE=槡EC2+BC2=槡5,
π
因为AP=AB,∠PAB= ,所以△PAB为等边三角形,所以PB=2,
3
所以PB2+PE2=5=BE2,所以PB⊥PE
因为PB∩PA=P,PB,PA平面PAB,所以PE⊥平面PAB
又PE平面PBE,所以平面PBE⊥平面PAB…………………………………… 5分
(2)由(1)得PE⊥平面PAB,所以V =V ,
P-ABE E-PAB
1 π
由三角形面积公式得S = PA×PB×sin =槡3,
△PAB 2 3
1 1 槡3
故V =V = ×S ×PE= ×槡3×1= ………………………… 10分
P-ABE E-PAB 3 △PAB 3 3
1 1
由(1)得PE⊥PB,PE⊥PA,PA=PB=2,所以S =S = PB×PE= ×2×1=1,
△PAE △PBE 2 2
1 π
由三角形面积公式得S = PA×PB×sin =槡3,S =2,
△PAB 2 3 △EAB
故三棱锥E-PAB的表面积为S=S +S +S +S =1+1+2+槡3=4+槡3
△PAE △PEB △EAB △PAB
…………………………………………………………………………………… 15分
18(1)由0005×20×2+00075×20+002×20+a×20+00025×20=1,
可得a=001 ……………………………………………………………………… 5分
(2)由(1)知样本数据中数学考试成绩90分以下学生所占比例为01+01+015=035,
110分以下学生所占比例为035+04=075,
05-035
因此,中位数一定位于[90,110)内,所以中位数=90+ =975,
002
根据率分布直方图,设平均数为 —x,
则
—x=40×01+60×01+80×015+100×04+120×02+140×005=93(分);
据此可以估计该校高一上学期期末数学考试成绩的中位数约为975分,平均数约为
93分 ……………………………………………………………………………… 10分
(3)由题意[50,70)分数段的人数为100×01=10,[70,90)分数段的人数为100×015=
15,用按比例分配的分层随机抽样的方法抽取5名学生,则需在[50,70)分数段内抽取
2人,分别记为A,A,[70,90)分数段内抽取3人,分别记为B,B,B
1 2 1 2 3
设“从这5名学生中任取2人,至少有1人成绩在[50,70)内”为事件A,
则样本空间 Ω={AA,AB,AB,AB,AB,AB,AB,BB,BB,BB},共包含
1 2 1 1 1 2 1 3 2 1 2 2 2 3 1 2 1 3 2 3
7
10个样本点,而事件A包含7个样本点,所以P(A)= ,故抽取的这2名学生至少有
10
7
1人成绩在[50,70)内的概率为 ……………………………………………… 17分
10
宣城市高一数学参考答案第2页(共3页)
{#{QQABSYCEggggAIJAAQgCUQFYCgOQkBEACQgOhFAMoAAAAAFABAA=}#}19(1)因为PA⊥平面ABCD,而AD平面ABCD,所以PA⊥AD,又AD⊥PB,PB∩PA=P,
PB,PA平面PAB,所以AD⊥平面PAB,而AB平面PAB,所以AD⊥AB
因为BC2+AB2=AC2,所以BC⊥AB,根据平面知识可知AD∥BC,再由前面推导知,
→ →
可知BC⊥平面PAB,所以BC⊥PB,所以向量CP在向量DA上的投影向量的模即为向量
→ → →
CB的模长1(或由上述推导知CP和DA的夹角是∠PCB。在Rt△PBC中,PB=槡7,
BC 1
BC=1,PC=2槡2,cos∠PCB= = ,
PC 2槡2
→ → →
故向量CP在DA上的投影向量的模为|CP|cos∠PCB=1)………………………… 5分
(2)“当AD⊥PB,且AD=1时”,则四边形 ABCD是长方形,可将四棱锥 P-ABCD补成一
个长、宽、高分别为槡3、1、2的长方体,则该长方体的外接球即为四棱锥 P-ABCD的外
接球,所以四棱锥P-ABCD有外接球,且该外接球半径为槡2,表面积S=8π;………
…………………………………………………………………………………… 10分
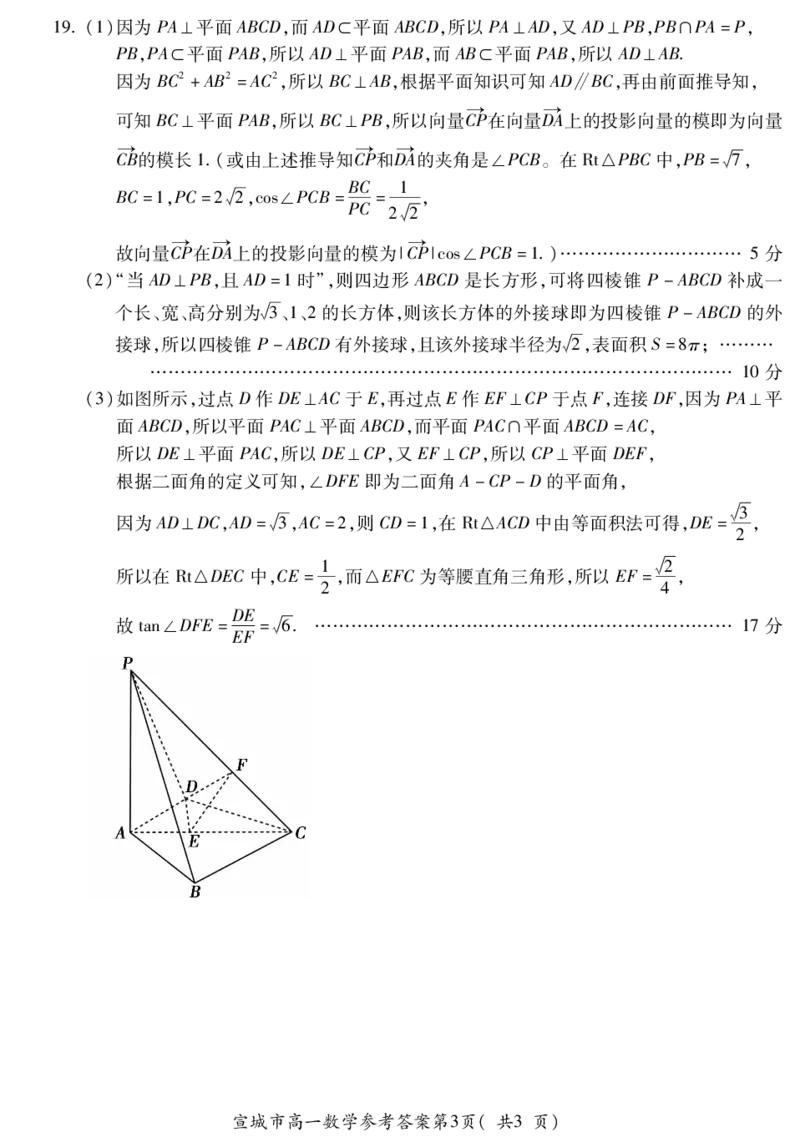
(3)如图所示,过点D作DE⊥AC于E,再过点E作EF⊥CP于点F,连接DF,因为PA⊥平
面ABCD,所以平面PAC⊥平面ABCD,而平面PAC∩平面ABCD=AC,
所以DE⊥平面PAC,所以DE⊥CP,又EF⊥CP,所以CP⊥平面DEF,
根据二面角的定义可知,∠DFE即为二面角A-CP-D的平面角,
槡3
因为AD⊥DC,AD=槡3,AC=2,则CD=1,在Rt△ACD中由等面积法可得,DE= ,
2
1 槡2
所以在Rt△DEC中,CE= ,而△EFC为等腰直角三角形,所以EF= ,
2 4
DE
故tan∠DFE= =槡6…………………………………………………………… 17分
EF
宣城市高一数学参考答案第3页(共3页)
{#{QQABSYCEggggAIJAAQgCUQFYCgOQkBEACQgOhFAMoAAAAAFABAA=}#}