文档内容
格致课堂
绝密★启用前
2019-2020学年度第二学期期中考试试卷(提升卷)
考试时间:120分钟;考试总分:150分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(每题5分,总分60分.)
1.已知 , 是虚数单位,若 与 互为共轭复数,则 ( )
a,b∈R i a-i 2+bi (a-bi) 2=
A.3+4i B.3-4i C.5-4i D.5+4i
【答案】B
【解析】依题意得 ,所以 .
a=2,b=1 (2-i) 2=3-4i
2.已知平面向量 ,则向量 ( )
A.平行于第一、三象限的角平分线 B.平行于y轴
C.平行于第二、四象限的角平分线 D.平行于x轴
【答案】B
【解析】由题:平面向量 ,
则向量 ,所以平行于y轴.
故选:B
3.若复数 (i为虚数单位),则 为( )
A. B.120° C.240° D.210°
【答案】C
【解析】由 ,得复数z对应的点在第三象限,格致课堂
且 ,
所以 .
故选:C.
4.在△ABC中,角 对边分别为 .若 , ,则 ( )
A. B. C. D.
【答案】C
【解析】根据正弦定理 , ,故选
C.
5.已知 , 是不共线的非零向量,则下列各式中 与 不共线的是( )
A. , B. ,
C. , D. ,
【答案】D
【解析】选项A中, ,则 与 共线.不符合题意,排除选项A.
选项B中, ,则 与 共线. 不符合题意,排除选项B.
选项C中, ,则 与 共线. 不符合题意,排除选项C.
选项D中,假设 与 共线,则 , 为实数,则 ,
∴格致课堂
∴ ,这样的 不存在,因此假设不成立,所以 与 不共线.符合题意.
故选:D
6.已知平面向量 , 夹角为 ,且 , ,则 与 的夹角是( )
A. B. C. D.
【答案】A
【解析】由题意可知: ,
则: ,
且: ,
设所求向量的夹角为 ,
有: ,则 与 的夹角是 .
本题选择A选项.
7.欧拉公式eix=cos x+isin x(i为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大
到复数,建立了三角函数和指数函数的关系,它在复变函数论里非常重要,被誉为“数学中的天桥”.根
据欧拉公式可知,e2i表示的复数在复平面中对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
【解析】由题意得,e2i=cos 2+isin 2,
∴复数在复平面内对应的点为(cos 2,sin 2).
∵2∈ ,
∴cos 2∈(-1,0),sin 2∈(0,1),格致课堂
∴e2i表示的复数在复平面中对应的点位于第二象限,
故选B.
8.设 为虚数单位, ,则实数
A.2 B.1
C.0 D.−1
【答案】C
【解析】由 ,得 ,所以 ,故选C.
9.在 中, ,其面积 ,则 夹角的取值范围为( )
A. B. C. D.
【答案】B
【解析】设| 与 的夹角为
.
故选B.
c
10.在 ABC 中,内角 B,C 对的边分别为 b, c .若C 2B ,则b的取值范围为( )
1
( ,1)
A. [2,2] B. 2 C. (0,2) D. (1,2)格致课堂
【答案】D
【解析】由正弦定理得 ,又由题意知 ,则 ,即
.故选D.
11.在 中, 是 的重心,且 ,其中 , , 分别是角 , ,
的对边,则 ( )
A.30° B.60° C.120° D.150°
【答案】A
【解析】在 中, 是 的重心,根据三角形重心性质有 ,
由题: ,所以 ,
由余弦定理得 ,
在 中,
故选:A
12.已知点 是边长为2的正方形 所在平面内一点,若 ,则 的最大值是(
)
A. B. C. D.
【答案】C
【解析】由 , ,得 ,即
点 在以点 为圆心,1为半径的圆周上运动,所以 的最大值为 ,
故选:C.格致课堂
第II卷(非选择题)
二、填空题(每题5分,总分20分.)
13.已知三点 , , 共线,则x为________.
7
【答案】
2
【解析】设 ,
所以
所以 ,
所以 , ,所以 .
14.不共线向量 , 满足 ,且 ,则 与 的夹角为________.
【答案】
【解析】由垂直可知 =0,即 , , ,又因为
,所以 .填 (或 ).
15. _______________.
【答案】
【解析】
=格致课堂
故答案为: .
16.在 中,角 , , 的对边分别为 , , ,已知 ,
若 的面积为 ,则当 的值最小时 的周长为____________.
【答案】
【解析】由 及正弦定理可得 ,
所以由余弦定理的推论可得 ,因为 ,所以 .
因为 的面积为 ,所以 ,即 ,
所以 ,当且仅当 时取等号,所以 的最小值为 ,
此时 , ,所以△ABC是等边三角形,故 的值最小时△ABC的周长为 .
三、解答题(17题10分,18-22题各12分,总分70分.)
17.已知向量 与 的夹角为60°,| |=1,| |=2格致课堂
(1)求(2 ﹣ )• ;
(2)求:|2 + |.
【答案】(1)1;
(2) .
【解析】(1)
(2) = .
18.已知复数 (其中 是虚数单位, ).
(1)若复数 是纯虚数,求 的值;
(2)求 的取值范围.
【答案】(1) ;(2) .
【解析】(1)
,
若复数 是纯虚数,则 ,所以 .
(2)由(1)得 , ,
,
因为 是开口向上的抛物线,有最小值 ;格致课堂
所以 .
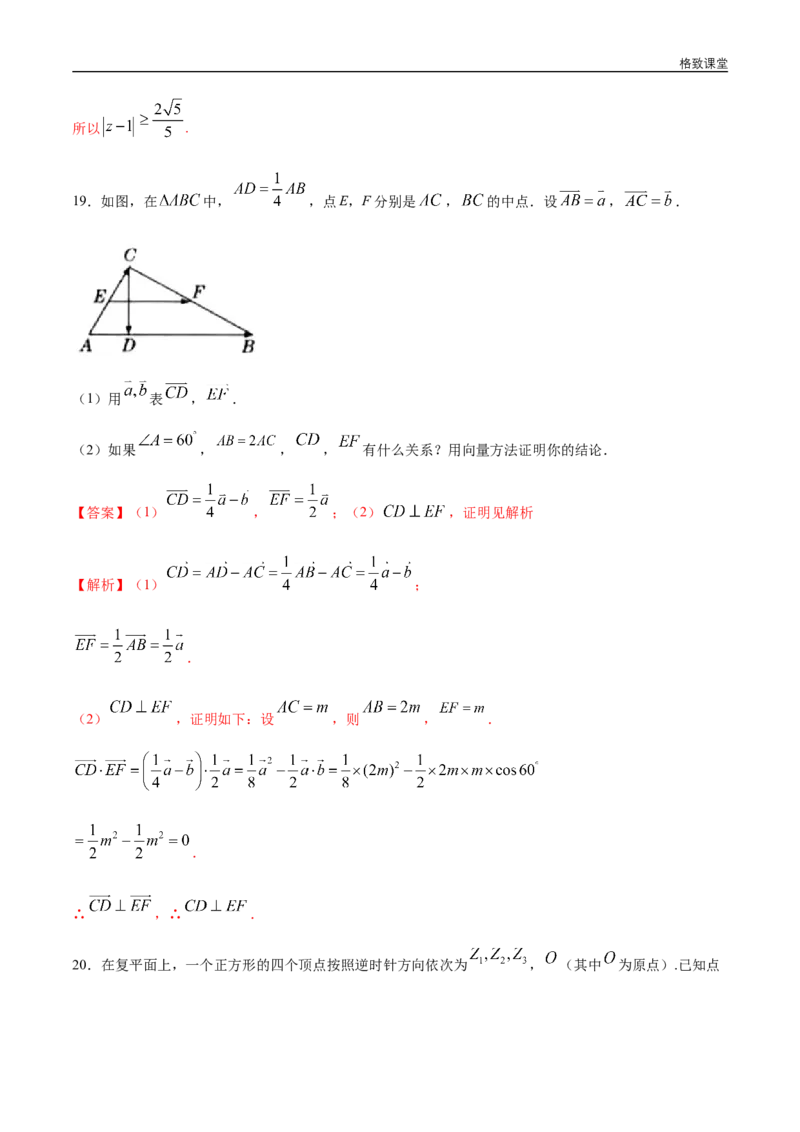
19.如图,在 中, ,点E,F分别是 , 的中点.设 , .
(1)用 表 , .
(2)如果 , , , 有什么关系?用向量方法证明你的结论.
【答案】(1) , ;(2) ,证明见解析
【解析】(1) ;
.
(2) ,证明如下:设 ,则 , .
.
∴ ,∴ .
20.在复平面上,一个正方形的四个顶点按照逆时针方向依次为 , (其中 为原点).已知点格致课堂
对应的复数 ,求 和 分别对应的复数 .
【答案】 , .
【解析】根据题意画出草图,如图所示.
由复数运算的几何意义知
,
.
21.在 中, 、 、 分别是角 、 、 的对边,且 .
(1)若 ,求 ;
(2) , ,求 的面积.格致课堂
【答案】(1) ;(2) .
【解析】(1)根据余弦定理及 ,得 ,
,即 , .
, , ,即 , ;
(2) , , ,
,则 , ,即 ,
, 的面积 .
22.在海岸A处,发现北偏东 方向,距离A为 n mile的B处有一艘走私船,在A处北偏西
方向,距离A为2 n mile的C处有一艘缉私艇奉命以 n mile / h的速度追截走私船,此时,走私船
正以10 n mile / h的速度从B处向北偏东 方向逃窜,问缉私艇沿什么方向行驶才能最快追上走私船?并
求出所需时间.(本题解题过程中请不要使用计算器,以保证数据的相对准确和计算的方便)格致课堂
【答案】缉私艇沿北偏东60°方向行驶才能最快追上走私船,这需 小时
【解析】
设缉私艇追上走私船需t小时,
则BD=10 t n mile CD= t n mile
∵∠BAC=45°+75°=120°
∴在△ABC中,由余弦定理得
即
由正弦定理得
∴ ∠ABC=45°,
∴BC为东西走向
∴∠CBD=120°
在△BCD中,由正弦定理得
∴ ∠BCD=30°,∴ ∠BDC=30°
∴
即
∴ (小时)
答:缉私艇沿北偏东60°方向行驶才能最快追上走私船,这需 小时.格致课堂