文档内容
期末模拟卷3
一.选择题(共8小题)
1.复数z满足z(1+i)=1﹣i,则z的虚部等于( )
A.﹣i B.﹣1 C.0 D.1
【分析】推导出z= = =﹣i,由此能求出z的虚部.
【解答】解:∵复数z满足z(1+i)=1﹣i,
∴z= = = =﹣i,
∴z的虚部为﹣1.
故选:B.
2.在一个随机试验中,彼此互斥的事件A,B,C,D发生的概率分别为0.1,0.1,0.4,
0.4,则下列说法正确的是( )
A.A与B+C是互斥事件,也是对立事件
B.B+C与D是互斥事件,也是对立事件
C.A+B与C+D是互斥事件,但不是对立事件
D.A+C与B+D是互斥事件,也是对立事件
【分析】根据题意,结合互斥、对立事件的定义分析选项,可得ABC错误,D正确,即
可得答案.
【解答】解:根据题意,依次分析选项:
对于A,事件A,B,C,D彼此互斥,则A与B+C是互斥事件,但P(A)+P(B+C)
≠1,则A与B+C不是对立事件,A错误;
对于B,事件A,B,C,D彼此互斥,则B+C与D是互斥事件,但P(B+C)+P(D)
≠1,则A与B+C不是对立事件,A错误;
对于C,事件A,B,C,D彼此互斥,则A+B与C+D是互斥事件,但P(A+B)+P
(C+D)=1,则A与B+C是对立事件,C错误;
对于D,事件A,B,C,D彼此互斥,则A+C与B+D是互斥事件,但P(A+C)+P
(B+D)=1,则A+C与B+D是对立事件,D正确;
故选:D.3.已知△ABC中,AB=2,BC=3,AC= ,则cosB=( )
A. B. C. D.
【分析】由已知结合余弦定理即可直接求解.
【解答】解:由余弦定理可得,cosB= = = .
故选:C.
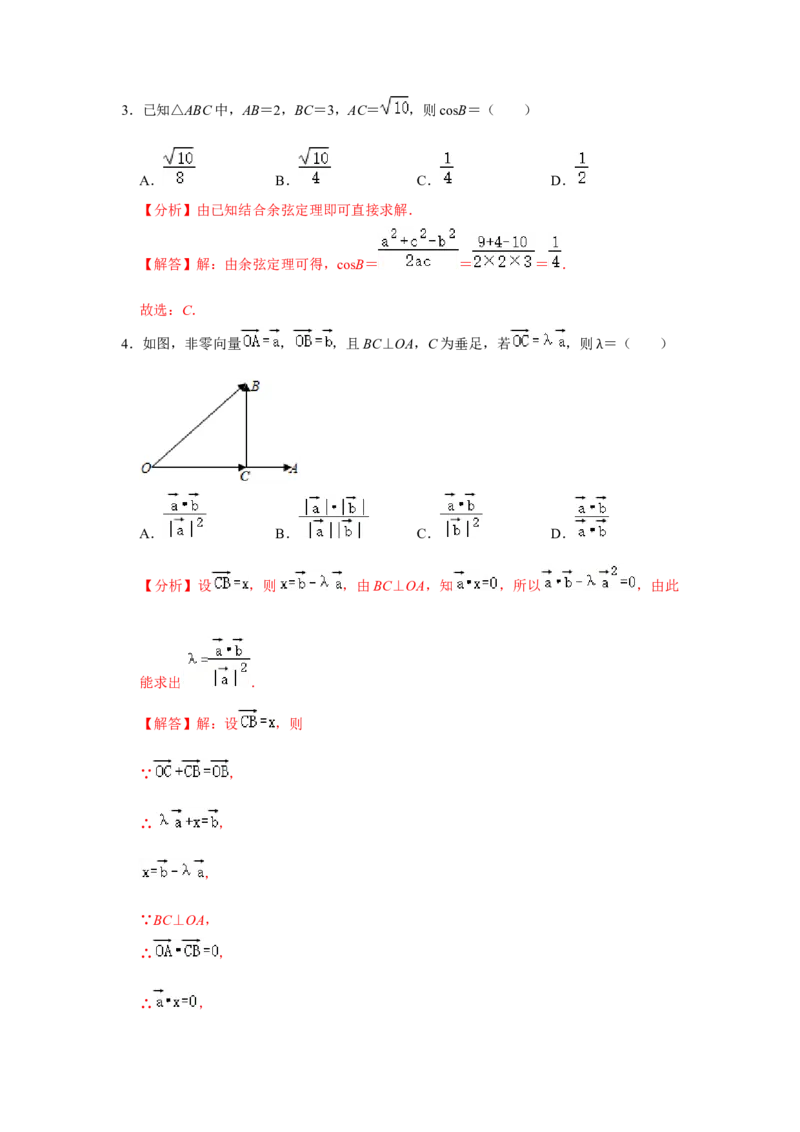
4.如图,非零向量 , ,且BC⊥OA,C为垂足,若 ,则 =( )
λ
A. B. C. D.
【分析】设 ,则 ,由BC⊥OA,知 ,所以 ,由此
能求出 .
【解答】解:设 ,则
∵ ,
∴ ,
,
∵BC⊥OA,
∴ ,
∴ ,∴ ,
∴ .
故选:A.
5.某班统计一次数学测验的平均分与方差,计算完毕以后才发现有位同学的卷子还未登分,
只好重算一次.已知原平均分和原方差分别为 、s2,新平均分和新方差分别为 、
s 2,若此同学的得分恰好为 ,则( )
1
A. = ,s2=s 2 B. = ,s2<s 2
1 1
C. = ,s2>s 2 D. < ,s2=s 2
1 1
【分析】根据平均数和方差的公式计算比较即可.
【解答】解:设这个班有n个同学,数据分别是a ,a ,…a…,a ,
1 2 i n
第i个同学没登录,
第一次计算时总分是(n﹣1) ,
方差是s2= [ +… + +…+ ]
第二次计算时, = = ,
方差 = [ +… + + +…+ ]=
s2,
故s2> ,
故选:C.
6.如图所示,一个水平放置的平面图形的斜二测直观图是等腰梯形 OA'B'C',且直观图
OA'B'C'的面积为2,则该平面图形的面积为( )A.2 B.4 C.4 D.2
【分析】结合S原图 =2 S直观图 ,可得答案.
【解答】解:由已知直观图OA'B'C'的面积为2,
∴原来图形的面积S=2×2 =4 ,
故选:B.
7.某实验单次成功的概率为0.8,记事件A为“在实验条件相同的情况下,重复 3次实验,
各次实验互不影响,则3次实验中至少成功2次”,现采用随机模拟的方法估计事件 A
的概率:先由计算机给出0~9十个整数值的随机数,指定0,1表示单次实验失败,
2,3,4,5,6,7,8,9表示单次实验成功,以3个随机数为组,代表3次实验的结果
经随机模拟产生了20组随机数,如表:
752 029 714 985 034
437 863 694 141 469
037 623 804 601 366
959 742 761 428 261
根据以上方法及数据,估计事件A的概率为( )
A.0.384 B.0.65 C.0.9 D.0.904
【分析】由随机模拟实验结合图表计算即可得解.
【解答】解:由随机模拟实验可得:
“在实验条件相同的情况下,重复3次实验,各次实验互不影响,则3次实验中最多成
功1次”共141,601两组随机数,
则“在实验条件相同的情况下,重复3次实验,各次实验互不影响,则3次实验中至少
成功2次”共20﹣2=18组随机数,
即事件A的概率为 =0.9,
故选:C.
8.已知三棱锥P﹣ABC的各顶点都在同一球面上,且 PA⊥平面ABC,AB=2,AC=1,∠ACB=90°,若该棱锥的体积为 ,则此球的表面积为( )
A.16 B.20 C.8 D.5
【分析π】直接利用锥体的体积π,锥体和球的关系及π勾股定理的应用求出球π的半径,进一
步求出球的表面积.
【解答】解:由∠ACB=90°,PA⊥平面ABC,得PB就是三棱锥外接球的直径,
如图所示:
易得 ,
所以 ,
,
即PA=4,
则 ,
故三棱锥外接球的半径为 .
所以三棱锥外接球的表面积S=4 R2=20 ,
故选:B. π π
二.多选题(共4小题)
9.某公司生产三种型号的轿车,产量分别为1500辆,6000辆和2000辆.为检验该公司的
产品质量,公司质监部要抽取57辆进行检验,则下列说法正确的是( )
A.应采用分层随机抽样抽取
B.应采用抽签法抽取
C.三种型号的轿车依次应抽取9辆,36辆,12辆
D.这三种型号的轿车,每一辆被抽到的概率都是相等的【分析】直接利用分层抽样的应用和比值的应用确定选项 A正确,选项B错误,选项
CD错误.
【解答】解:某公司生产三种型号的轿车,产量分别为 1500辆,6000辆和2000辆为检
验该公司的产品质量,公司质监部要抽取57辆进行检验,
所以该检验采用分层抽样的方法,故选项A正确,选项B错误.
对于选项C:1500+6000+2000=9500,所以抽样为 , ,
,故选项C正确.
对于选项D:对于分层抽样的每一辆轿车被抽到的可能性相等,故选项D正确.
故选:ACD.
10.下列叙述中,正确的是( )
A.若| |=0,则 =0 B.若| |=0,则 ∥
C.若 ∥ , ∥ ,则 ∥ D.若 = , = ,则 =
【分析】由平面向量的定义及零向量的应用可依次对选项判断
【解答】解:对于A:零向量记作 ,其长度是0,因此 = ,故A错误;
对于B:长度为0的向量是零向量,并与任意向量平行,故B正确;
对于C:当 = 时, 与 不一定共线,故C错误;
对于D:向量相等具有传递性,故D正确.
故选:BD.
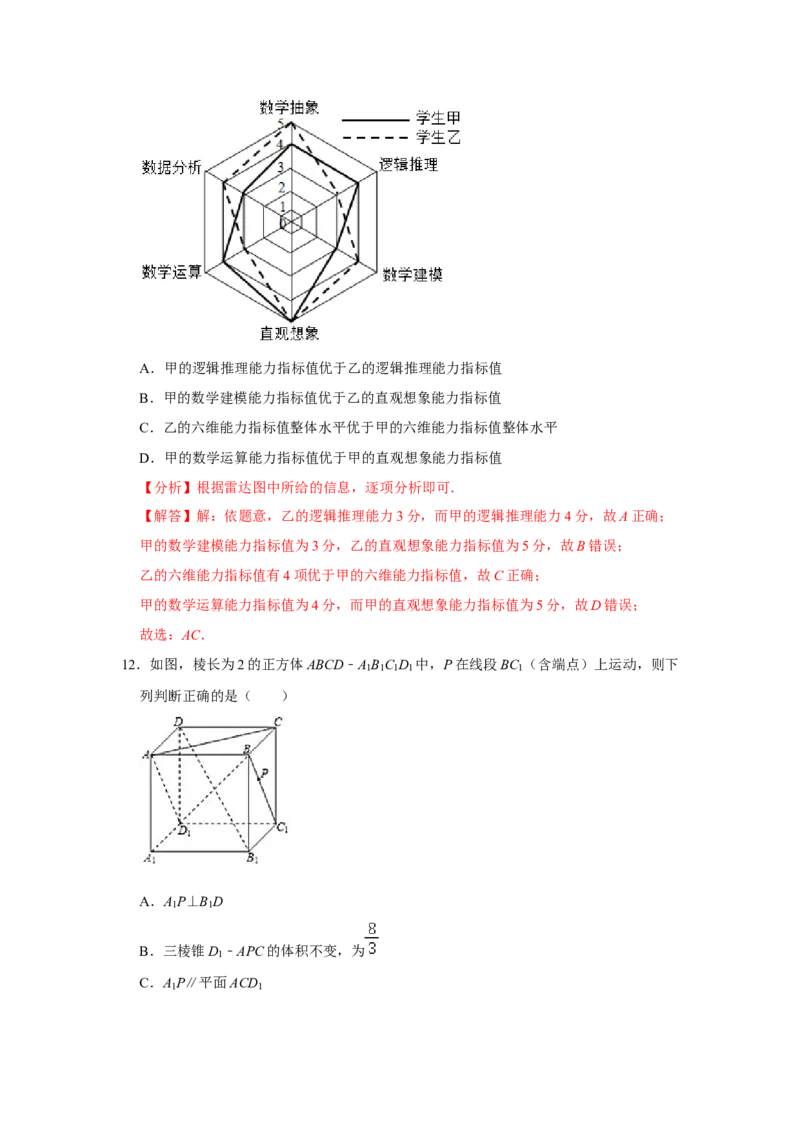
11.雷达图是以从同一点开始的轴上表示的三个或更多个定量变量的二维图表的形式显示
多变量数据的图形方法.为比较甲,乙两名学生的数学学科素养的各项能力指标值(满
分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,例如图中甲的数学抽
象指标值为4,乙的数学抽象指标值为5,则下面叙述正确的是( )A.甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
【分析】根据雷达图中所给的信息,逐项分析即可.
【解答】解:依题意,乙的逻辑推理能力3分,而甲的逻辑推理能力4分,故A正确;
甲的数学建模能力指标值为3分,乙的直观想象能力指标值为5分,故B错误;
乙的六维能力指标值有4项优于甲的六维能力指标值,故C正确;
甲的数学运算能力指标值为4分,而甲的直观想象能力指标值为5分,故D错误;
故选:AC.
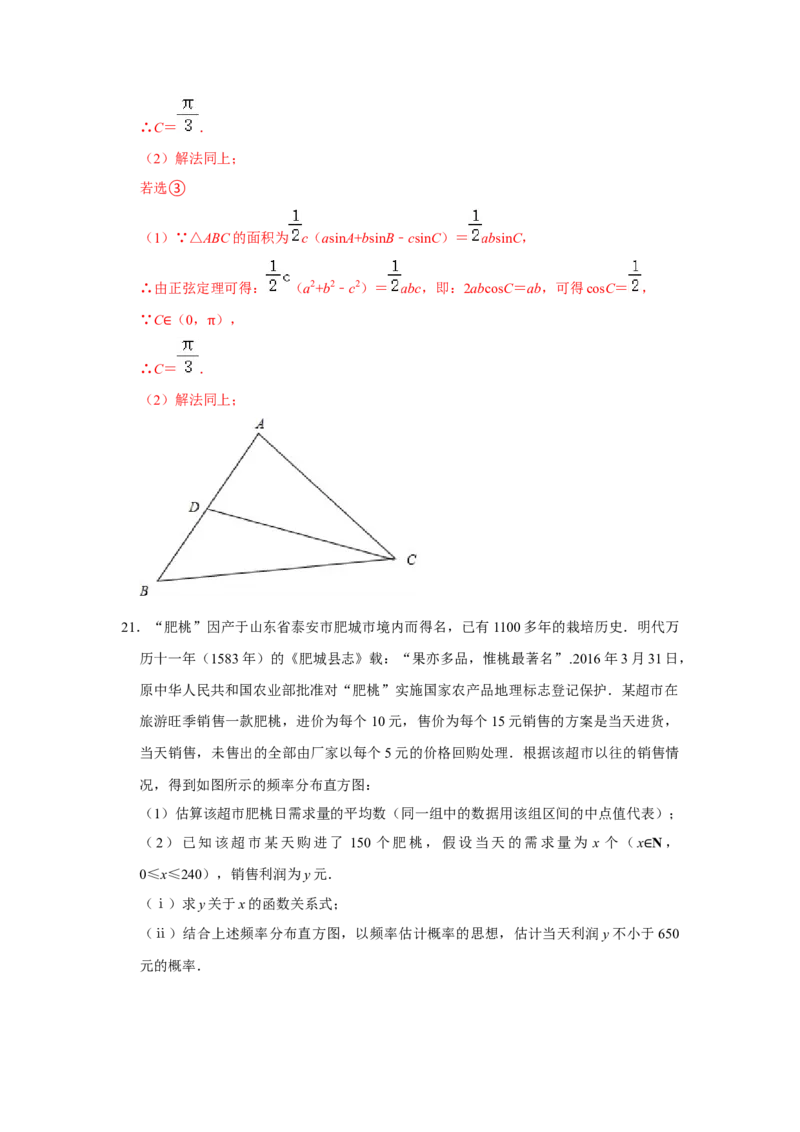
12.如图,棱长为2的正方体ABCD﹣A B C D 中,P在线段BC (含端点)上运动,则下
1 1 1 1 1
列判断正确的是( )
A.A P⊥B D
1 1
B.三棱锥D ﹣APC的体积不变,为
1
C.A P∥平面ACD
1 1D.A P与D C所成角的范围是
1 1
【分析】对于 A,推导出 B D⊥BC ,B D⊥A C ,从而 B D⊥平面 A C B,进而
1 1 1 1 1 1 1 1
A P⊥B D,;对于B,推导出BC ∥平面ACD ,从而P到ACD 的距离是定值,以D
1 1 1 1 1 1
为原点,D A 为x轴,D C 为y轴,D D为z轴,建立空间直角坐标系,利用向量法求
1 1 1 1 1
出三棱锥D ﹣APC的体积为 ;对于C,由AD ∥BC ,CD ∥A B,得平面AD C∥平
1 1 1 1 1 1
面BC A ,从而A P∥平面ACD ;对于D,当P与B重合时,A P与D C所成角为0,
1 1 1 1 1 1
当P与C 重合时,A P与D C所成角为 .
1 1 1
【解答】解:棱长为2的正方体ABCD﹣A B C D 中,P在线段BC (含端点)上运动,
1 1 1 1 1
对于A,B C⊥BC ,CD⊥BC ,B C∩CD=C,B C、CD 平面CDB ,
1 1 1 1 1 1
∴BC 1 ⊥平面CDB 1 ,∵B 1 D 平面CDB 1 ,∴B 1 D⊥BC 1 , ⊂
同理,B
1
D⊥A
1
C
1
,∵A
1
C
1
∩⊂BC
1
=C
1
,A
1
C
1
、BC
1
平面A
1
C
1
B,∴B
1
D⊥平面A
1
C
1
B,
∵A 1 P 平面A 1 C 1 B,∴A 1 P⊥B 1 D,故A正确; ⊂
对于B⊂,∵P在线段BC
1
(含端点)上运动,BC
1
∥AD
1
,BC
1
平面ACD
1
,AD
1
平面
ACD , ⊄ ⊂
1
∴BC ∥平面ACD ,∴P到ACD 的距离是定值,
1 1 1
以D 为原点,D A 为x轴,D C 为y轴,D D为z轴,建立空间直角坐标系,
1 1 1 1 1 1
D (0,0,0),A(2,0,2),C(0,2,2),B(2,2,2),
1
=(2,0,2), =(0,2,2), =(2,2,2),
设平面D AC的法向量 =(x,y,z),
1
则 ,取x=1,得 =(1,1,﹣1),
∴P到平面D AC的距离d= = = ,
1
∴三棱锥D ﹣APC的体积为:
1
= = == ,故B错误;
对于C,∵AD ∥BC ,CD ∥A B,AD ∩CD =D ,BC ∩A B=B,
1 1 1 1 1 1 1 1 1
∴平面AD C∥平面BC A ,∵A P 平面BC A ,∴A P∥平面ACD ,故C正确;
1 1 1 1 1 1 1 1
对于D,∵P在线段BC
1
(含端点)⊂上运动,
∴当P与B重合时,A P与D C所成角为0,
1 1
当P与C 重合时,A P与D C所成角为 ,故D错误.
1 1 1
故选:AC.
三.填空题(共4小题)
13.如表为武汉市2018年月平均降水量:
月份 1 2 3 4 5 6 7 8 9 10 11 12
月平均降水 5.8 4.8 5.3 4.6 5.6 5.6 5.1 7.1 5.6 5.3 6.4 6.6
量/cm
则武汉市2018年月平均降水量的三个四分位数分别为 5.2 cm, 5.6 cm, 6.1
cm.
【分析】根据四分位数的定义即可求出.
【解答】解:将数据从小到大排序:4.6,4.8,5.1,5.3,5.3,5.6,5.6,5.6,5.8,
6.4,6.6,7.1.
第二分位数为: =5.6,
第一分位数为: =5.2,第三分位数为: =6.1,
故答案为:5.2,5.6,6.1.
14.已知i是虚数单位,则 = 1+ 4 i .
【分析】把分子分母同时乘以分母的共轭复数,化简得答案.
【解答】解: = .
故答案为:1+4i.
15.已知等边△ABC,D 为 BC 中点,若点 M 是△ABC 所在平面上一点,且满足
,则 = 0 .
【分析】选择 , 为平面向量的一组基底,由平面向量线性运算及平面向量基本定
理即可得解.
【解答】解:由已知有| |=| |
因为 = •( )
= •( ﹣ )
= •( ﹣ )
= •( )
= ﹣
=
=0,
故答案为:0.
16.某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样大的四面体得
到的(如图).则该几何体共有 14 个面;如果被截正方体的棱长是50cm,那么石凳的表面积是 7500+250 0 cm2.
【分析】由题意知截去的八个四面体,再加上6个正方形,该几何体共有14个面;由
此计算该几何体的表面积.
【解答】解:由题意知,截去的八个四面体是全等的正三棱锥,8个底面三角形,再加
上6个小正方形,
所以该几何体共有14个面;
如果被截正方体的棱长是50cm,那么石凳的表面积是
S表面积 =8× ×25 ×25 ×sin60°+6×25 ×25 =(7500+2500 )(cm2).
故答案为:14,7500+2500 .
四.解答题(共6小题)
17.设 =(2,0), =(1, ).
(1)若( ﹣ )⊥ ,求实数 的值;
λ λ
(2)若 =x +y (x,y R),且| |=2 , 与 的夹角为 ,求x,y的值.
【分析】(1)由题可知,∈ ﹣ =(2﹣ ,﹣ ),于是推出( ﹣ )• =(2﹣
λ λ λ λ
,﹣ )•(1, )=0,结合平面向量数量积的坐标运算解之即可;
λ λ
(2) =(2x+y, y),由| |=2 ,可得x2+xy+y2=3①,由 与 的夹角为 ,
可得x+2y=3②,联合①②解方程组即可.
【解答】解:(1)∵ =(2,0), =(1, ),∴ ﹣ =(2﹣ ,﹣ ),
λ λ λ
∵( ﹣ )⊥ ,
λ
∴( ﹣ )• =(2﹣ ,﹣ )•(1, )=2﹣ ﹣3 =0,
λ λ λ λ λ
解得 = .
(2)λ =x +y =x(2,0)+y(1, )=(2x+y, y),
∵| |=2 ,∴ =12,即x2+xy+y2=3①,
∵ 与 的夹角为 ,
∴cos = = = ,即x+2y=3②,
由①②解得x=1,y=1或x=﹣1,y=2.
18.甲,乙,丙三名射击运动员分别对一目标射击1次,甲射中的概率为0.90,乙射中的
概率为0.95,丙射中的概率为0.95.求:
(1)三人中恰有一人没有射中的概率;
(2)三人中至少有两人没有射中的概率.(精确到0.001)
【分析】(1)利用相互独立事件乘法公式和互斥事件概率加法公式能求出三人中恰有
一人没有射中的概率;
(2)利用相互独立事件乘法公式和互斥事件概率加法公式能求出三人中至少有两人没
有射中的概率.
【解答】解:(1)甲,乙,丙三名射击运动员分别对一目标射击1次,
甲射中的概率为0.90,乙射中的概率为0.95,丙射中的概率为0.95.
∴三人中恰有一人没有射中的概率为:
P=0.9×0.95×0.05+0.9×0.05×0.95+0.1×0.95×0.95=0.17575≈0.176.
(2)三人中至少有两人没有射中的概率为:
P=0.9×0.05×0.05+0.1×0.95×0.05+0.1×0.05×0.95+0.1×0.05×0.05=0.012.
19.如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC= ,O,M分别为AB,VA的中点.
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB.
【分析】(1)利用三角形的中位线得出OM∥VB,利用线面平行的判定定理证明VB∥
平面MOC;
(2)证明:OC⊥平面VAB,即可证明平面MOC⊥平面VAB.
【解答】证明:(1)∵O,M分别为AB,VA的中点,∴OM∥VB,
∵VB 平面MOC,OM 平面MOC,
∴VB⊄∥平面MOC. ⊂
(2)∵AC=BC,O为AB的中点,
∴OC⊥AB,
∵平面VAB⊥平面ABC,OC 平面ABC,
∴OC⊥平面VAB, ⊂
∵OC 平面MOC,
∴平面⊂MOC⊥平面VAB.
20.请从下面三个条件中任选一个,补充在下面的横线上,并作答.
① = ;
②2ccosC=acosB+bcosA;
③△ABC的面积为 c(asinA+bsinB﹣csinC).
已知△ABC的内角A,B,C的对边分别为a,b,c,且_____.
(1)求C;
(2)若D为AB中点,且c=2,CD= ,求a,b.
【分析】若选①,(1)由已知利用正弦定理可得 a2+b2﹣c2=ab,利用余弦定理可得cosC= ,结合C的范围即可求解C的值.(2)由题意利用三角形的中线定理可得:
b2+a2=8,又由余弦定理可得4=a2+b2﹣ab,联立方程可求a,b的值.
若选②,(1)由正弦定理化简已知等式可得:2sinCcoC=sinC,结合sinC≠0,可求
cosC= ,结合范围C (0, ),可求C的值.(2)解法同上;
∈ π
若选③,(1)由已知利用三角形的面积公式,正弦定理可得cosC= ,结合C的范围,
可求C的值.(2)解法同上;
【解答】解:若选①,
(1)∵ = ,
∴由正弦定理可得: = ,整理可得:a2+b2﹣c2=ab,
∴cosC= = ,
∵C (0, ),
∈ π
∴C= .
(2)∵C= ,D为AB中点,且c=2,CD= ,
∴AD=BD=1,
∴由三角形的中线定理可得:b2+a2=2(AD2+CD2),即b2+a2=2(1+3)=8,①
又∵由余弦定理c2=a2+b2﹣2abcosC,可得:4=a2+b2﹣ab,②
∴由①②可得ab=4,进而解得a=b=2.
若选②
(1)∵2ccosC=acosB+bcosA,
∴由正弦定理可得:2sinCcoC=sinAcosB+sinBcosA=sin(A+B)=sinC,
∵sinC≠0,
∴可得cosC= ,
∵C (0, ),
∈ π∴C= .
(2)解法同上;
若选③
(1)∵△ABC的面积为 c(asinA+bsinB﹣csinC)= absinC,
∴由正弦定理可得: (a2+b2﹣c2)= abc,即:2abcosC=ab,可得cosC= ,
∵C (0, ),
∈ π
∴C= .
(2)解法同上;
21.“肥桃”因产于山东省泰安市肥城市境内而得名,已有1100多年的栽培历史.明代万
历十一年(1583年)的《肥城县志》载:“果亦多品,惟桃最著名”.2016年3月31日,
原中华人民共和国农业部批准对“肥桃”实施国家农产品地理标志登记保护.某超市在
旅游旺季销售一款肥桃,进价为每个10元,售价为每个15元销售的方案是当天进货,
当天销售,未售出的全部由厂家以每个5元的价格回购处理.根据该超市以往的销售情
况,得到如图所示的频率分布直方图:
(1)估算该超市肥桃日需求量的平均数(同一组中的数据用该组区间的中点值代表);
(2)已知该超市某天购进了 150 个肥桃,假设当天的需求量为 x 个(x N,
0≤x≤240),销售利润为y元. ∈
(ⅰ)求y关于x的函数关系式;
(ⅱ)结合上述频率分布直方图,以频率估计概率的思想,估计当天利润y不小于650
元的概率.【分析】(1)先利用各组频率之和为1,求出a的值,再利用每组区间的中点值乘以该
组的频率依次相加,即可估算出平均数;
(2)( i)分情况讨论,得到y关于x的分段函数的函数关系式即可;( ii)利润
y≥650,当且仅当日需求量x [140,240]. 由频率分布直方图求出x [140,240]的频
率,以频率估计概率的思想,∈能估计当天利润y不小于650元的概率.∈
【解答】解:(1)由题意可知:(0.00125+a+0.0075+0.00625+a+0.0025)×40=1,
解得a=0.00375;
所 以 平 均 数 =
(20×0.00125+60×0.00375+100×0.0075+140×0.00625+180×0.00375+220×0.0025)×40
=0.05×20+0.15×60+0.3×100+0.25×140+0.15×180+0.1×220=124;
(2)( i)当x [150,240]时,y=150×(20﹣15)=750,
当x [0,150)时∈,y=(20﹣15)x﹣(150﹣x)(15﹣10)=10x﹣750,
∈
故y= ,(x N);
∈
( ii)由( i)可知,利润y≥650,当且仅当日需求量x [140,240].
由频率分布直方图可知,日需求量x [140,240]的频率约∈为 0.125+0.15+0.1=0.375,
以频率估计概率的思想,估计当天利∈润y不小于650元的概率为0.375.
22.《九章算术》是中国古代的一部数学专著,是《算经十书》中最重要的一部,成于公
元一世纪左右.它是一本综合性的历史著作,是当时世界上最简练有效的应用数学,它
的出现标志着中国古代数学形成了完整的体系.《九章算术》中将由四个直角三角形组
成的四面体称为“鳖臑”,已知在三棱锥P﹣ABC中,PA⊥平面ABC.
(1)从三棱锥P﹣ABC中选择合适的两条棱填空: BC ⊥ AB ,则三棱锥P﹣ABC为“鳖臑”;
(2)如图,已知AD⊥PB,垂足为D,AE⊥PC,垂足为E,∠ABC=90°.
(ⅰ)证明:平面ADE⊥平面PAC;
(ⅱ)设平面ADE与平面ABC的交线为l,若PA=2 ,AC=2,求二面角E﹣l﹣C的
大小.
【分析】(1)利用题中所给定义,直接写出答案即可;
(2)(i)先证明BC⊥平面PAB,再证AD⊥平面PBC,由此可得PC⊥平面ADE,再
根据面面垂直的判定得证;
(ii)设DE∩BC=F,连接AF,可知∠EAC即为二面角E﹣l﹣C的一个平面角,再转
化到△PAC中解三角形即可.
【解答】解:(1)由题意,四个直角三角形组成的四面体称为“鳖臑”,而 PA⊥平面
ABC,
要使三棱锥P﹣ABC为“鳖臑”,则只需BC⊥AB或BC⊥AC或BC⊥PB或BC⊥PC;
(2)(i)证明:∵PA⊥平面ABC,BC 平面ABC,
∴PA⊥BC, ⊂
又∠ABC=90°,即BC⊥AB,PA∩AB=A,PA,AB 平面PAB,
∴BC⊥平面PAB, ⊂
又AD 平面PAB,
∴BC⊥⊂AD,
又AD⊥PB,PB∩BC=B,PB,BC 平面PBC,
∴AD⊥平面PBC, ⊂
又PC 平面PBC,
⊂∴AD⊥PC,
又AE⊥PC,AD∩AE=A,AD,AE 平面ADE,
∴PC⊥平面ADE, ⊂
又PC 平面PAC,
∴平面⊂PAC⊥平面ADE;
(ii)由题意知,在平面PBC中,直线DE与直线BC相交,
如图所示,
设DE∩BC=F,连接AF,则AF即为l,
∵PC⊥平面AED,l 平面AED,
∴PC⊥l, ⊂
∵PA⊥平面ABC,l 平面ABC,
∴PA⊥l, ⊂
又PA∩PC=P,PA,PC 平面PAC,
∴l⊥平面PAC, ⊂
又AE,AC 平面APAC,
∴AE⊥l,A⊂C⊥l,
∴∠EAC即为二面角E﹣l﹣C的一个平面角,
在△PAC中,PA⊥AC, ,
∴PC=4,
又AE⊥PC,
∴ ,
∴ ,
∴∠EAC=30°,即二面角E﹣l﹣C的大小为30°.