文档内容
安徽六校教育研究会 2024 级高一新生入学素质测试
数学试题参考答案
一、单选题(共 10小题,每小题 3分,共 30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C B B A B C B D
二、填空题(共 4小题,每小题 3分,共 12分)
10 8
11.xy(x+2) 12.90 13. , 14.2 10
9 9
三、解答题(共 8小题,共 58分)
a+2 a+2
15.解:原式= ÷ 2分
a+3 (a+3)(a−3)
a+2 (a+3)(a−3)
= × =a−3 4分
a+3 a+2
将a =1代入,得:原式=1−3=−2. 5分
16.解:(1)将点A、B的坐标代入反比例函数表达式得:m=2×3=−2a,
解得:a =−3,m=6,
6
即反比例函数的表达式为:y = , 1分
x
2k+b=3 k =1
点B(−3,−2),将点A、B的坐标代入一次函数表达式得: ,解得 ,
−3k+b=−2 b=1
则一次函数的解析式为:y = x+1 3分
(2)设点C ( x,0 ) ,
由点A、B、C的坐标得,AB2 =50,AC2 =(x−2)2 +9,BC2 =(x+3)2 +4, 4分
∠BCA=90°,则AB2 = AC2 +BC2,即50=(x−2)2 +9+(x+3)2 +4
解得:x=3或−4(舍去),即点C(3,0). 6分
17.解:(1)设书架上数学书x本,则语文书(90−x)本,
根据题意得,0.8x+1.2(90−x)=84, 2分
解得x=60,所以90−x=30,
所以书架上数学书60本,语义书30本. 3分
(2)设数学书还可以摆m本,则10×1.2+0.8m≤84, 5分
学科网(北京)股份有限公司解得m≤90,所以数学书最多还可以摆90本. 6分
18.解:(1)本次调查的员工共有48÷30%=160(人),
90
表中x的值为160× =40;
360
故答案为:160,40; 2分
44
(2)360°× =99°,
160
所以在扇形统计图中,“国风古韵观赏线”对应的圆心角度数为99°; 4分
160−44−40−48
(3)200× =385(人),
160
所以估计选择“园艺小清新线”的员工人数为385人. 7分
19.解:在Rt△ABC中,AB=8尺,∠ACB=73.4°,
8 8
∴tan73.4°= ,tan73.4°≈3.35,∴BC ≈ ≈2.4(尺); 2分
BC 3.35
在Rt△ABD中,AB=8尺,∠ADB=26.6°,
8
∴tan26.6°= ,tan26.6°≈0.50,∴BD≈16.0(尺); 4分
BD
∴CD= BD−BC =16.0−2.4=13.6(尺), 5分
观察可知,春分和秋分时日影顶端为CD的中点,
13.6
2.4+ =9.2(尺),
2
∴春分和秋分时日影长度为9.2尺. 7分
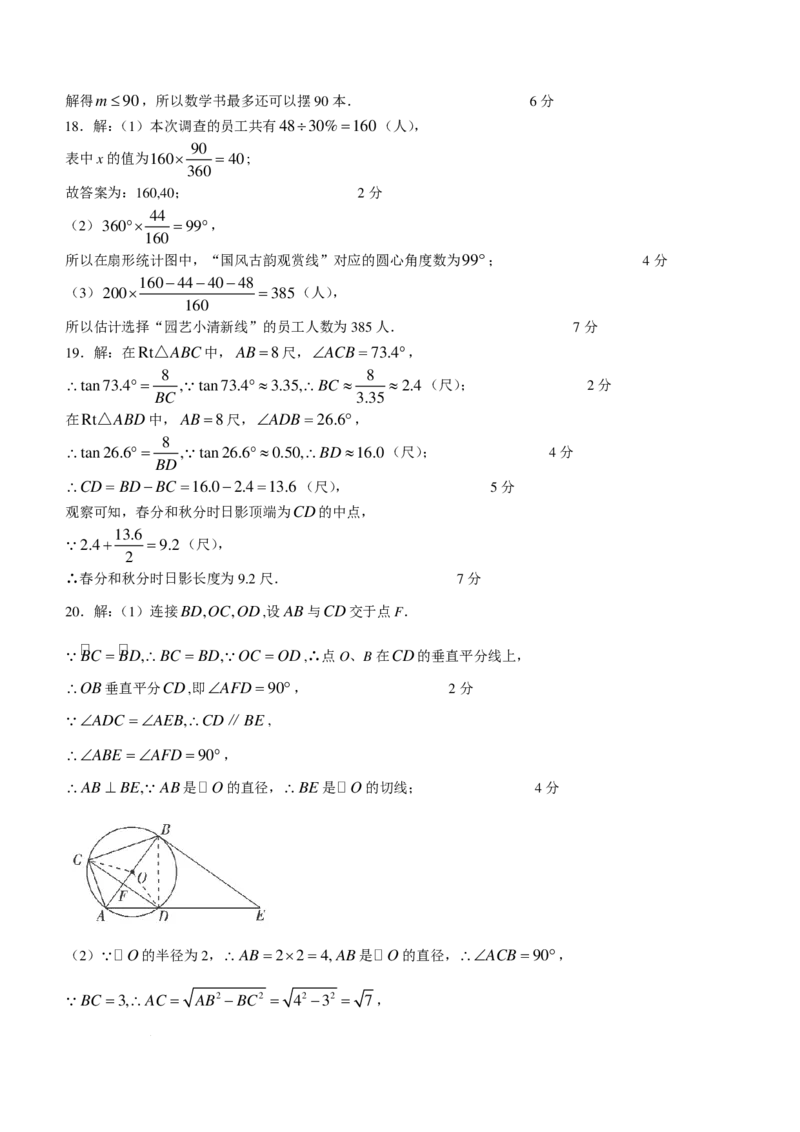
20.解:(1)连接BD,OC,OD,设AB与CD交于点F.
BC = BD,∴BC = BD,OC =OD,∴点O、B在CD的垂直平分线上,
∴OB垂直平分CD,即∠AFD=90°, 2分
∠ADC =∠AEB,∴CD∥BE,
∴∠ABE =∠AFD=90°,
∴AB⊥ BE,AB是 O的直径,∴BE是 O的切线; 4分
(2) O的半径为2,∴AB=2×2=4,AB是 O的直径,∴∠ACB=90°,
BC =3,∴AC = AB2 −BC2 = 42 −32 = 7,
学科网(北京)股份有限公司AC 7
∴tan∠ABC = = , 5分
BC 3
AC = AC,∴∠ADC =∠ABC,∠AEB=∠ADC,∴∠AEB=∠ABC,
7
∴tan∠AEB=tan∠ABC = . 7分
3
21.解:(1)∵点P(2,−3)在二次函数y =ax2 +bx−3的图象上,
∴4a+2b−3=−3,解得b=−2a, 1分
∴抛物线为y =ax2 −2ax−3,
−2a
∴抛物线的对称轴为直线x=− =1,∴m=1; 2分
2a
(2)∵点Q(1,−4)在y =ax2 −2ax−3的图象上,
∴a−2a−3=−4,解得a =1, 3分
∴抛物线为y = x2 −2x−3=(x−1)2 −4, 4分
将该二次函数的图象向上平移5个单位长度,得到新的二次函数为:y =(x−1)2 −4+5=(x−1)2 +1,
5分
0≤ x≤4,
∴当x=1时,函数有最小值为1,当x=4时,函数有最大值为(4−1)2 +1=10,
∴当0≤ x≤4时,新的二次函数的最大值与最小值的和为11; 6分
(3)y =ax2 −2ax−3的图象与x轴交点为( x ,0 ) , ( x ,0 )( x < x )
1 2 1 2
3
∴x +x =2,x x =− 7分
1 2 1 2 a
12 3
∴x −x = ( x +x )2 −4x x = 4+ =2 1+ , 8分
2 1 1 2 1 2 a a
4< x −x <6
2 1
3 3
∴4<2 1+ <6,解得