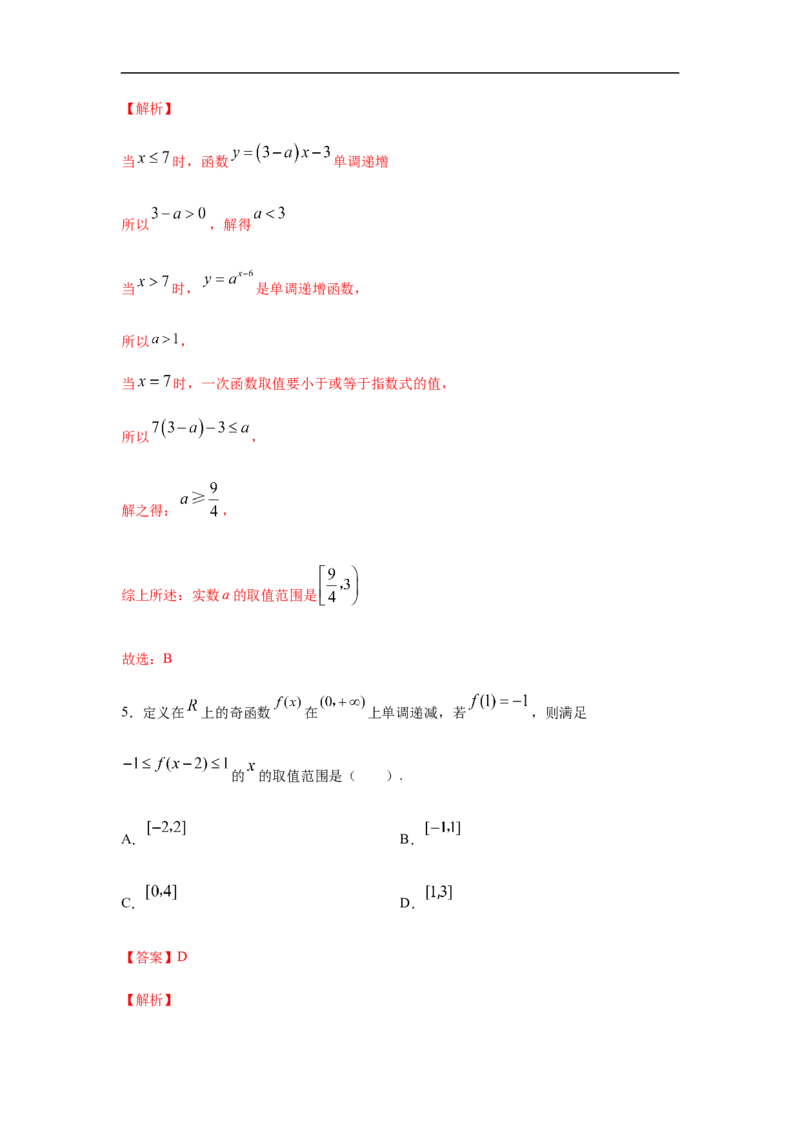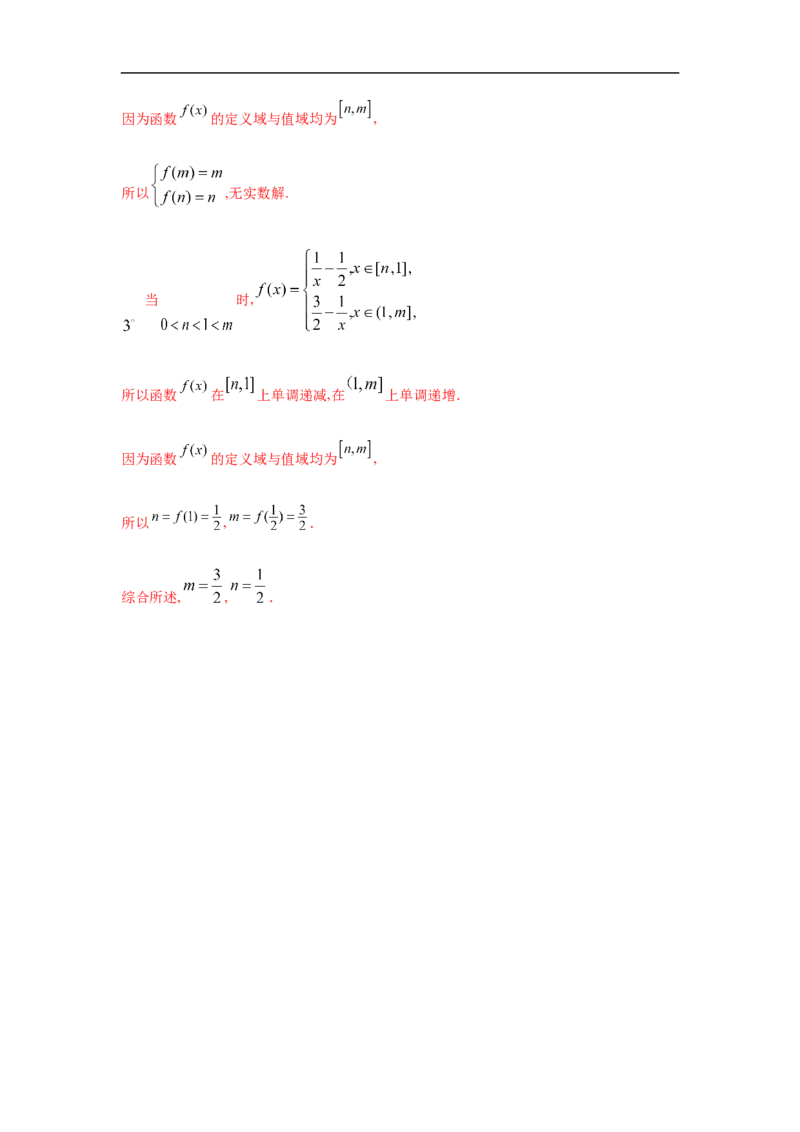文档内容
第3单元 函数概念与性质(基础篇)
基础知识讲解
1.分段函数的解析式求法及其图象的作法
【基础知识】
分段函数是定义在不同区间上解析式也不相同的函数.若函数在定义域的不同子集上
的对应法则不同,可用几个式子来表示函数,这种形式的函数叫分段函数.已知一个分段
函数在某一区间上的解析式,求此函数在另一区间上的解析式,这是分段函数中最常见的
问题.
【技巧方法】
求解函数解析式的几种常用方法
1、待定系数法,如果已知函数解析式的构造时,用待定系数法;
2、换元法或配凑法,已知复合函数f[g(x)]的表达式可用换元法,当表达式较简单时也
可用配凑法;
3、消参法,若已知抽象的函数表达式,则用解方程组消参的方法求解f(x);
另外,在解题过程中经常用到分类讨论、等价转化等数学思想方法.分段函数是一类重要
的函数模型.解决分段函数问题,关键抓住在不同的段内研究问题.
2.函数单调性的性质与判断
【基础知识】
一般地,设函数f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个
自变量x ,x ,
1 2
当x <x 时,都有f(x )<f(x ),那么就说函数f(x)在区间D上是增函数;当x >x
1 2 1 2 1 2
时,都有f(x )<f(x ),那么就说函数f(x)在区间D上是减函数.
1 2若函数f(x)在区间D上是增函数或减函数,则称函数f(x)在这一区间具有(严格
的)单调性,区间D叫做y=f(x)的单调区间.
【技巧方法】
证明函数的单调性用定义法的步骤:①取值;②作差;③变形;④确定符号;⑤下结论.
利用函数的导数证明函数单调性的步骤:
第一步:求函数的定义域.若题设中有对数函数一定先求定义域,若题设中有三次函
数、指数函数可不考虑定义域.
第二步:求函数f(x)的导数f′(x),并令f′(x)=0,求其根.
第三步:利用f′(x)=0的根和不可导点的x的值从小到大顺次将定义域分成若干个
小开区间,并列表.
第四步:由f′(x)在小开区间内的正、负值判断f(x)在小开区间内的单调性;求极
值、最值.
第五步:将不等式恒成立问题转化为f(x)max≤a或f(x)min≥a,解不等式求参数的
取值范围.
第六步:明确规范地表述结论
3.复合函数的单调性
【基础知识】
复合函数就是由两个或两个以上的基本函数构成,这种函数先要考虑基本函数的单调
性,然后再考虑整体的单调性.平常常见的一般以两个函数的为主.
【技巧方法】
求复合函数y=f(g(x))的单调区间的步骤:
(1)确定定义域;
(2)将复合函数分解成两个基本初等函数;
(3)分别确定两基本初等函数的单调性;(4)按“同增异减”的原则,确定原函数的单调区间.
4.奇函数、偶函数
【奇函数】
如果函数f(x)的定义域关于原点对称,且定义域内任意一个x,都有f(﹣x)=
﹣f(x),那么函数f(x)就叫做奇函数,其图象特点是关于(0,0)对称.
【技巧方法】
①如果函数定义域包括原点,那么运用f(0)=0解相关的未知量;
②若定义域不包括原点,那么运用f(x)=﹣f(﹣x)解相关参数;
③已知奇函数大于 0 的部分的函数表达式,求它的小于 0 的函数表达式,如奇函数 f
(x),当x>0时,f(x)=x2+x
那么当x<0时,﹣x>0,有f(﹣x)=(﹣x)2+(﹣x)⇒﹣f(x)=x2﹣x⇒f(x)=﹣
x2+x
【偶函数】
如果函数f(x)的定义域关于原点对称,且定义域内任意一个x,都有
f(﹣x)=f(x),那么函数f(x)就叫做偶函数,其图象特点是关于y轴对称.
【技巧方法】
①运用f(x)=f(﹣x)求相关参数,如y=ax3+bx2+cx+d,那么a+c是多少?
②结合函数图象关于y轴对称求函数与x轴的交点个数或者是某个特定的值,如偶函数 f
(﹣2)=0,周期为2,那么在区间(﹣2,8)函数与x轴至少有几个交点.
5.函数奇偶性的性质与判断
【基础知识】
①如果函数f(x)的定义域关于原点对称,且定义域内任意一个 x,都有f(﹣x)=﹣f
(x),那么函数f(x)就叫做奇函数,其图象特点是关于(0,0)对称.②如果函数f(x)的定义域关于原点对称,且定义域内任意一个x,都有f(﹣x)=f(x),那么函数
f(x)就叫做偶函数,其图象特点是关于y轴对称.
【技巧方法】
①奇函数:如果函数定义域包括原点,那么运用f(0)=0解相关的未知量;
②奇函数:若定义域不包括原点,那么运用f(x)=﹣f(﹣x)解相关参数;
③偶函数:在定义域内一般是用f(x)=f(﹣x)这个去求解;
④对于奇函数,定义域关于原点对称的部分其单调性一致,而偶函数的单调性相反.
6.函数解析式的求解及常用方法
【基础知识】
通过求解函数的解析式中字母的值,得到函数的解析式的过程就是函数的解析式的求解.
【技巧方法】
求解函数解析式的几种常用方法主要有
1、换元法;2、待定系数法;3、凑配法;4、消元法;5、赋值法等.
7.幂函数的单调性、奇偶性及其应用
【基础知识】
1.幂函数定义:
一般地,函数y=xa(a R)叫做幂函数,其中x是自变量,a是常数.
∈
(1)指数是常数;
(2)底数是自变量;
(3)函数式前的系数都是1;
(4)形式都是y=xa,其中a是常数.
8.幂函数的性质【基础知识】
所有的幂函数在(0,+∞)上都有各自的定义,并且图象都过点(1,1).
(1)当a>0时,幂函数y=xa有下列性质:
a、图象都通过点(1,1)(0,0);
b、在第一象限内,函数值随x的增大而增大;
c、在第一象限内,a>1时,图象开口向上;0<a<1时,图象开口向右;
d、函数的图象通过原点,并且在区间[0,+∞)上是增函数.
(2)当a<0时,幂函数y=xa有下列性质:
a、图象都通过点(1,1);
b、在第一象限内,函数值随x的增大而减小,图象开口向上;
c、在第一象限内,当x从右趋于原点时,图象在y轴上方趋向于原点时,图象在y轴右方
无限逼近y轴,当x趋于+∞时,图象在x轴上方无限地逼近x轴.
(3)当a=0时,幂函数y=xa有下列性质:
a、y=x0是直线y=1去掉一点(0,1),它的图象不是直线.
9.五个常用幂函数的图象和性质
(1)y=x; (2)y=x2; (3)y=x3; (4)y= ; (5)y=x﹣1
y=x y=x2 y=x3 y=x﹣1
y=
定义域 R R R [0,+∞) {x|x≠0}
值域 R [0,+∞) R [0,+∞) {y|y≠0}
奇偶性 奇 偶 奇 非奇非偶 奇
单调性 增 x [0,+∞)时,增 增 增 x (0,+∞)时,减
∈ ∈x (﹣∞,0]时, x (﹣∞,0)时,减
减
∈ ∈
公共点 (1,1) (1,1)(0,0) (1,1) (1,1) (1,1)
(0,0) (0,0) (0,0)
10.幂函数的奇偶性
(1)所有的幂函数在(0,+∞)都有定义,并且函数图象都通过点(1,1).
(2)如果a>0,则幂函数的图象过点(0,0),(1,1),并在[0,+∞)上为增函数.
(3)如果a<0,则幂函数的图象过点(1,1),并在(0,+∞)上为减函数.
(4)当a为奇数时,幂函数为奇函数,当a为偶数时,幂函数为偶函数.
11.函数最值的应用
【基础知识】
函数的最值顾名思义就是指函数在某段区间内的最大值和最小值.在日常生活中我们
常常会遇到如何使成本最低,如何用料最少,如何占地最小等等的问题,这里面就可以转
化为求函数的最值问题.另外,最值可分为最大值和最小值.
【技巧方法】
这种题的关键是把现实的问题转化为数学上的问题,具体的说是转化为函数最值问题,
这里面需要同学们要具有转化思维,具有一定的建模能力,在很多高考题中也常常以大题
的形式出现,所以务必引起重视.这里我们以具体的例题来讲解.
12.根据实际问题选择函数类型
【基础知识】
1.实际问题的函数刻画
在现实世界里,事物之间存在着广泛的联系,许多联系可以用函数刻画.用函数的观点看
实际问题,是学习函数的重要内容.【技巧方法】
常用到的五种函数模型:
①直线模型:一次函数模型y=kx+b(k≠0),图象增长特点是直线式上升(x的系数k>
0),通过图象可以直观地认识它,特例是正比例函数模型y=kx(k>0).
②反比例函数模型:y= (k>0)型,增长特点是y随x的增大而减小.
③指数函数模型:y=a•bx+c(b>0,且b≠1,a≠0),其增长特点是随着自变量的增大,函
数值增大的速度越来越快(底数b>1,a>0),常形象地称为指数爆炸.
④对数函数模型,即y=mlog x+n(a>0,a≠1,m≠0)型,增长特点是随着自变量的增大,
a
函数值增大越来越慢(底数a>1,m>0).
⑤幂函数模型,即y=a•xn+b(a≠0)型,其中最常见的是二次函数模型:y=ax2+bx+c
(a≠0),其特点是随着自变量的增大,函数值先减小后增大(a>0).
在以上几种函数模型的选择与建立时,要注意函数图象的直观运用,分析图象特点,分析
变量x的范围,同时还要与实际问题结合,如取整等.
习题演练
一.选择题(共12小题)
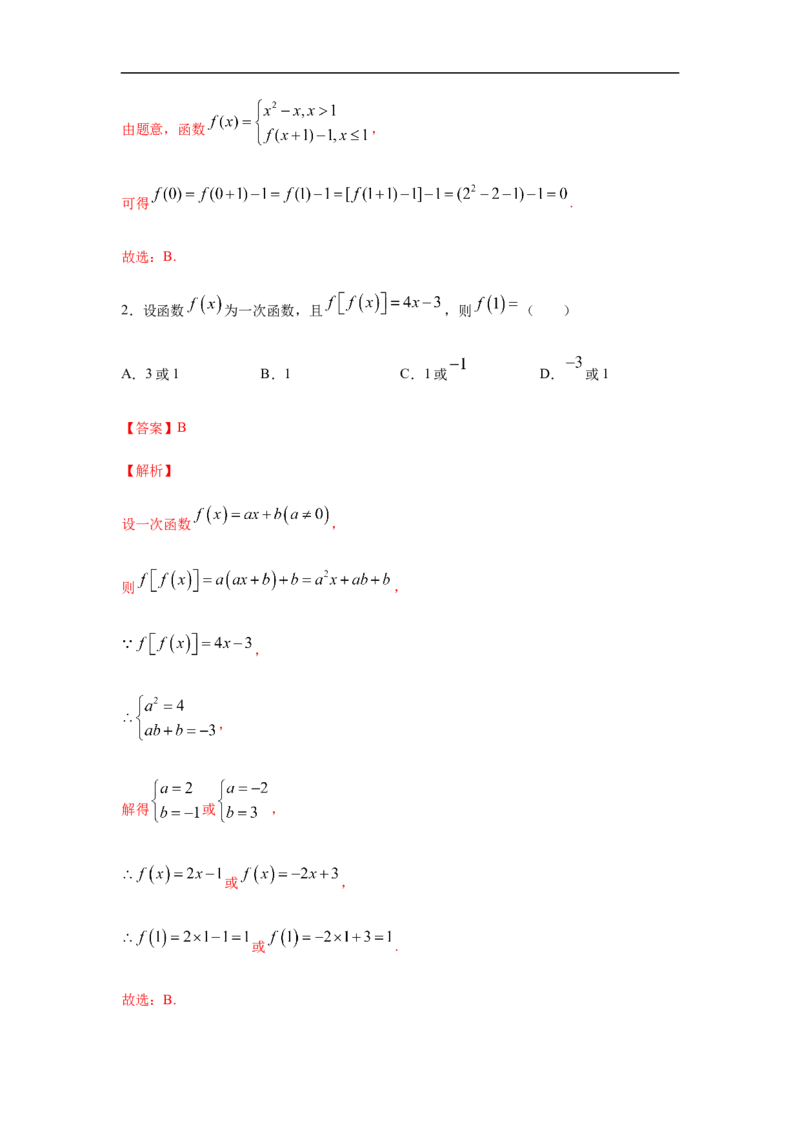
1.若函数 ,则 ( )
A.-1 B.0 C.1 D.2
【答案】B
【解析】由题意,函数 ,
可得 .
故选:B.
2.设函数 为一次函数,且 ,则 ( )
A.3或1 B.1 C.1或 D. 或1
【答案】B
【解析】
设一次函数 ,
则 ,
,
,
解得 或 ,
或 ,
或 .
故选:B.3.若函数 |在区间 上不是单调函数,则实数 的取值范
围是( )
A. B.
C. D.
【答案】B
【解析】
,分 三种情况讨论.
当 时, ,所以 ;
当 时, , 在 上显然单调;
当 时, ,所以 .
综上: 或 .
故选B.
4.若函数 单调递增,则实数a的取值范围是( )
A. B. C. D.
【答案】B【解析】
当 时,函数 单调递增
所以 ,解得
当 时, 是单调递增函数,
所以 ,
当 时,一次函数取值要小于或等于指数式的值,
所以 ,
解之得: ,
综上所述:实数a的取值范围是
故选:B
5.定义在 上的奇函数 在 上单调递减,若 ,则满足
的 的取值范围是( ).
A. B.
C. D.
【答案】D
【解析】由题意,函数 为奇函数且在 单调递减,
因为 ,可得 ,
要使不等式 成立,即 成立,
则实数 满足 ,解得 ,
所以实数 的取值范围为 .
故选:D.
6.若函数 的最小值3,则实数 的值为( )
A.5或8 B. 或5 C. 或 D. 或
【答案】D
【解析】
由题意,①当 时,即 , ,则当 时,
,解得 或 (舍);②当 时,即 , ,则当 时,
,解得 (舍)或 ;③当 时,
即 , ,此时 ,不满足题意,所以 或 ,故选
D.
7.已知定义在 上的奇函数 ,对任意实数 ,恒有 ,且当
时, ,则 ( )
A.6 B.3 C.0 D.
【答案】B
【解析】
由题得 ,所以函数的周期为 .
由题得
,
,,
所以 ,
所以
.
故选:B.
8.满足 的实数m的取值范围是( ).
A. B.
C. D.
【答案】D
【解析】
幂函数 在 为减函数,且函数值为正,
在 为减函数,且函数值为负,
等价于,或 或 ,
解得 或 或 ,
所以不等式的解集为 .
故选:D.
9.已知函数 是幂函数且是 上的增函数,则 的值为(
)
A.2 B.-1 C.-1或2 D.0
【答案】B
【解析】
由题意得 ,
故选:B.
10.已知 ,若 为负数,则 的取值范围是( )
A. B. C. D.
【答案】D
【解析】
,.
故选: .
11.若定义在 的奇函数f(x)在 单调递减,且f(2)=0,则满足 的x的
取值范围是( )
A. B.
C. D.
【答案】D
【解析】
因为定义在 上的奇函数 在 上单调递减,且 ,
所以 在 上也是单调递减,且 , ,
所以当 时, ,当 时, ,
所以由 可得:
或 或
解得 或 ,
所以满足 的 的取值范围是 ,
故选:D.12.已知函数 是定义在 上的奇函数,且 ,当 时,
,则 ( )
A. B. C. D.
【答案】C
【解析】
由题意,函数 是定义在 上的奇函数,且 ,
可得 ,所以 ,
所以函数 是周期为4的周期函数,
又由当 时, ,
则 .
故选:C.
二.填空题(共6小题)
13.函数 ,则 ______.
【答案】1
【解析】根据题意, ,则 ;
故答案为1.
14.已知定义在 上的函数 的导函数为 ,若对于任意 都有
,且 ,则不等式 的解集为________.
【答案】
【解析】
即为 ,设函数 ,
则 ,所以 在 上单调递
减,
又因为 ,所以 ,不等式 可化为 ,
即 ,所以 ,故解集为 .
故答案为: .
15.已知函数 ,函数 ,则函数 的最小值是
_______.【答案】0
【解析】
解:当 时, 为单调增函数,则 ;
当 时, 为单调减函数,所以 ,
所以函数 的最小值是0.
故答案为:0.
16.已知奇函数 在定义域 上递减,且 ,则实数 的
取值范围是______.
【答案】
【解析】
由于 是定义在 上单调递减的奇函数,
所以由 ,得 ,
所以 ,解得 ,
所以实数 的取值范围是 .
故答案为: .17.已知函数 ,则不等式 的解
集是______.
【答案】
【解析】
,故 为奇函数,且单调递减,
则令 ,故 为奇函数且单调递减,故
等价于
,即 ,即
,解得
故答案为
18.已知函数 满足 ,函数 ,若函数
与 的图象共有12个交点,记作 ,则
的值为______.
【答案】72
【解析】因为 ,所以 关于点 成中心对称,又因为
,所以 也关于点 成中心对
称,所以 与 的图象的交点也关于点 成中心对称,不妨认为
,所以有 ,所以
.
三.解析题(共6小题)
19.已知定义在 上的函数 .
(1)若 ,求 的值;
(2)若 对于 恒成立,求实数 的取值范围.
【答案】(1) ,(2) .
【解析】
(1)当 时, ;当 时, ,由 可知:
,即 ,所以有 ,因为 ,解得 ,
故 ;
(2)当 时, ,即 ,
因为 ,故 ,
因为 ,所以 ,则m的取值范围是 .
20.根据下列条件,求f(x)的解析式.
(1)f(x)是一次函数,且满足3f(x+1)-f(x)=2x+9;
(2)f(x+1)=x2+4x+1;
(3) .
【答案】(1)f(x)=x+3;(2)f(x)=x2+2x-2;(3)
【解析】
(1)解由题意,设f(x)=ax+b(a≠0)
∵3f(x+1)-f(x)=2x+9
∴3a(x+1)+3b-ax-b=2x+9,
即2ax+3a+2b=2x+9,
由恒等式性质,得∴a=1,b=3
∴所求函数解析式为f(x)=x+3.
(2)设x+1=t,则x=t-1
f(t)=(t-1)2+4(t-1)+1
即f(t)=t2+2t-2.
∴所求函数解析式为f(x)=x2+2x-2.
(3)解 ,将原式中的x与 互换,得 .
于是得关于f(x)的方程组
解得 .
21.已知定义在 上的函数 对任意实数 都满足 ,且
,当 时, .
(1)证明: 在 上是减函数;
(2)解不等式
【答案】(1)证明见解析;(2) .
【解析】(1)因为任意实数 都满足 ,
令 ,则 ,∵ ,∴
当 时,则 ,∴ ,∵ ,∴
,
即 时, 恒成立,
设任意的 ,且 ,则 ,
∴ ,
即 在 上是减函数,
(2) ,
,
由(1)知 在 上为减函数,
得: ,故不等式的解集为 .
22.已知定义域为R的函数 是奇函数.
(1)求b的值;(2)判断函数 的单调性;
(3)若对任意的 ,不等式 恒成立,求k的取值范围.
【答案】(1)1;(2)减函数;(3) .
【解析】
(1)因为 是奇函数,所以 ,
即 ,∴
(2)由(1)知 ,
设 则
因为函数 在R上是增函数且 ,∴
又 ,∴ 即
∴ 在 上为减函数.
(3)因 是奇函数,从而不等式:
等价于 ,因 为减函数,由上式推得:
.即对一切 有: ,从而判别式 .
23.已知幂函数 为偶函数,且在区间 上是单调增函数
(1)求函数 的解析式;
(2)设函数 ,其中 .若函数 仅在
处有极值,求 的取值范围.
【答案】(1) ;(2)
【解析】
(1) 在区间 上是单调增函数,
即 又
而 时, 不是偶函数, 时, 是偶函数,
.
(2) 显然 不是方程 的根.
为使 仅在 处有极值,必须 恒成立,
即有 ,解不等式,得 .这时, 是唯一极值. .
24.已知函数 .
(1)若 时, ,求 的值;
(2)若 时,函数 的定义域与值域均为 ,求所有 值.
【答案】(1) (2) ,
【解析】
(1)因为 ,所以
所以 ,
所以 或 ,
因为 ,所以 .
(2) 当 时, 在 上单调递减,
因为函数 的定义域与值域均为 ,
所以 ,两式相减得 不合,舍去.
当 时, 在 上单调递增,因为函数 的定义域与值域均为 ,
所以 ,无实数解.
当 时,
所以函数 在 上单调递减,在 上单调递增.
因为函数 的定义域与值域均为 ,
所以 , .
综合所述, , .