文档内容
2023—2024 学年度下期高 2024 届入学考试
理科数学试卷
考试时间:120分钟 满分:150分
一、选择题:本题共 12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. 已知集合 , ,则 的真子集的个数为(
)
A. 9 B. 8 C. 7 D. 6
2. 若函数 是定义在 上的偶函数,则 ( )
A. B. C. D. 2
.
3 已知复数z满足 ,则 ( )
A. B. C. 1 D.
4. 已知 ,则 ( )
A. B. C. 30 D. 60
5. 已知正项等差数列 的前 项和为 ,且 , .则( )
.
A B.
C. D.
6. 已知 , ,则 ( )
A. B. C. D.
第1页/共9页
学科网(北京)股份有限公司7. 对于数列 ,若满足: ,则称 为数列 的“优值”,现已
知数列 的“优值” ,记数列 的前 项和为 ,则 的最大值为( )
A. B. C. D.
8. 在平面直角坐标系 中,已知圆 ,若圆 上存在点
P,由点P向圆C引一条切线,切点为M,且满足 ,则实数a的取值范围为( )
A. B. C. D.
9. 设函数 若存在 且 ,使得 ,
则 的取值范围是( )
A. B.
C. D.
10. 在四面体 中, , ,且 ,则该四面体的
外接球表面积为( )
A. B. C. D.
11. 从0,1,2,3,4,5,6,7,8,9这十个数字中任意取出三个不同的数,若这三个数的和为不小于9
的奇数,则不同的取法有( )种.
A. 54 B. 53 C. 47 D. 46
12. 定义在 上的可导函数 满足 ,当 时, ,若实数a
第2页/共9页
学科网(北京)股份有限公司满足 ,则a的取值范围为( )
A. B.
C. D.
二、填空题:本题共4小题,每小题5分,共20分.
13. 若双曲线 的一条渐近线与直线 平行,则双曲线的右焦点到一条渐近
线的距离为__________.
14. 在正方体 中, ,点 平面 ,点 F 是线段 的中点,若
,则当 的面积取得最小值时, _____________.
15. 设 数 列 满 足 , , , 令
,则数列 的前100项和为___________.
16. 已知函数 , ,若函数 有三个零点
,则 的取值范围是__________.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第 17~21题为必考题,
每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17. 2023年12月25日,由科技日报社主办,部分两院院士和媒体人共同评选出的2023年国内十大科技新
闻揭晓.某高校一学生社团随机调查了本校100名学生对这十大科技的了解情况,按照性别和了解情况分组,
得到如下列联表:
第3页/共9页
学科网(北京)股份有限公司比较了
不太了解 合计
解
男生 20 40 60
女生 20 20 40
合计 40 60 100
(1)判断是否有95%的把握认为对这十大科技的了解存在性别差异;
(2)若把这100名学生按照性别进行分层随机抽样,从中抽取5人,再从这5人中随机抽取2人,记抽取
的2人中女生数为 ,求 的分布列及 .
附:① ,其中 ;
②当 时有95%的把握认为两变量有关联.
18. 在锐角 中,角 所对应的边分别为 ,已知 .
(1)求 的值;
(2)若 ,求 面积的取值范围.
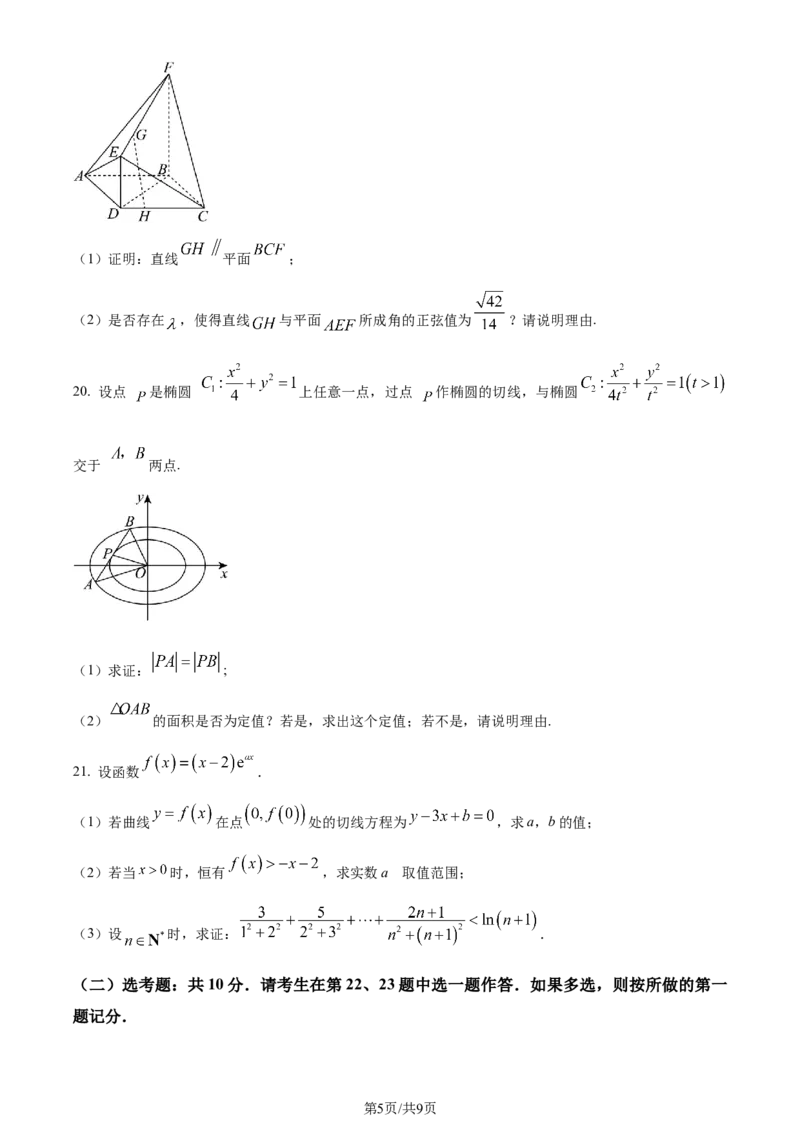
19. 如图,在多面体 中,四边形 为平行四边形,且 平
面 ,且 .点 分别为线段 上的动点,满足
.
第4页/共9页
学科网(北京)股份有限公司(1)证明:直线 平面 ;
(2)是否存在 ,使得直线 与平面 所成角的正弦值为 ?请说明理由.
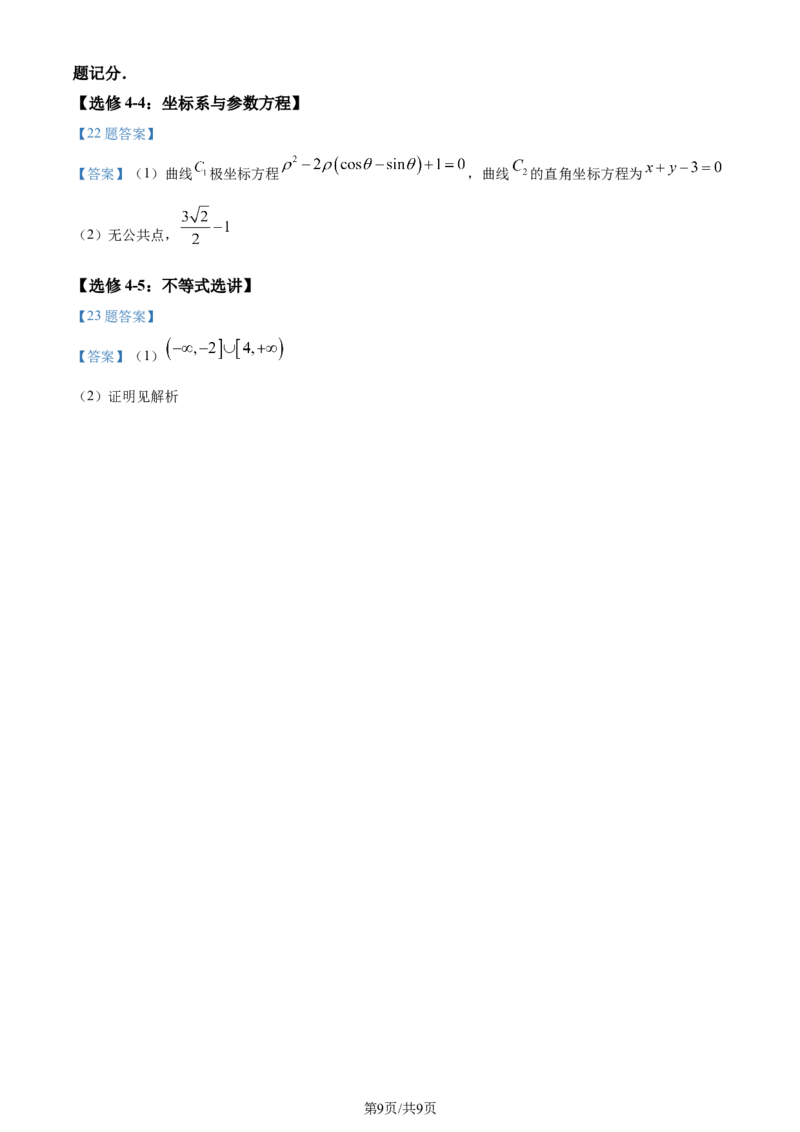
20. 设点 是椭圆 上任意一点,过点 作椭圆的切线,与椭圆
交于 两点.
(1)求证: ;
(2) 的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
21. 设函数 .
(1)若曲线 在点 处的切线方程为 ,求a,b的值;
的
(2)若当 时,恒有 ,求实数a 取值范围;
(3)设 时,求证: .
(二)选考题:共10分.请考生在第22、23题中选一题作答.如果多选,则按所做的第一
题记分.
第5页/共9页
学科网(北京)股份有限公司【选修4-4:坐标系与参数方程】
22. 在平面直角坐标系 中,曲线 的参数方程为 ( 为参数),以坐标原点 为极点,
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为 .
(1)写出曲线 的极坐标方程,曲线 的直角坐标方程;
(2)曲线 与曲线 ,如有公共点,求出公共点坐标;如无公共点,设 分别为曲线 与曲线 上
的动点,求线段 的最小值.
【选修4-5:不等式选讲】
23. 已知函数 .
(1)求不等式 的解集;
(2)设函数 的最小值为 ,若 且 ,求证: .
第6页/共9页
学科网(北京)股份有限公司2023—2024 学年度下期高 2024 届入学考试
理科数学试卷
考试时间:120分钟 满分:150分
一、选择题:本题共 12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
【1题答案】
【答案】C
【2题答案】
【答案】D
【3题答案】
【答案】C
【4题答案】
【答案】D
【5题答案】
【答案】C
【6题答案】
【答案】D
【7题答案】
【答案】D
【8题答案】
【答案】D
【9题答案】
【答案】A
【10题答案】
【答案】B
【11题答案】
【答案】B
【12题答案】
【答案】C
二、填空题:本题共4小题,每小题5分,共20分.
【13题答案】
第7页/共9页
学科网(北京)股份有限公司【答案】 ##0.5
【14题答案】
【答案】 ##
【15题答案】
【答案】
【16题答案】
【答案】
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第 17~21题为必考题,
每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
(一)必考题:共60分.
【17题答案】
【答案】(1)没有 (2)分布列见解析,
【18题答案】
【答案】(1)
(2)
【19题答案】
【答案】(1)证明见解析
(2)存在,理由见解析
【20题答案】
【答案】(1)见解析 (2)是定值,定值为
【21题答案】
【答案】(1)
(2)
(3)证明见解析
(二)选考题:共10分.请考生在第22、23题中选一题作答.如果多选,则按所做的第一
第8页/共9页
学科网(北京)股份有限公司题记分.
【选修4-4:坐标系与参数方程】
【22题答案】
【答案】(1)曲线 极坐标方程 ,曲线 的直角坐标方程为
(2)无公共点,
【选修4-5:不等式选讲】
【23题答案】
【答案】(1)
(2)证明见解析
第9页/共9页
学科网(北京)股份有限公司