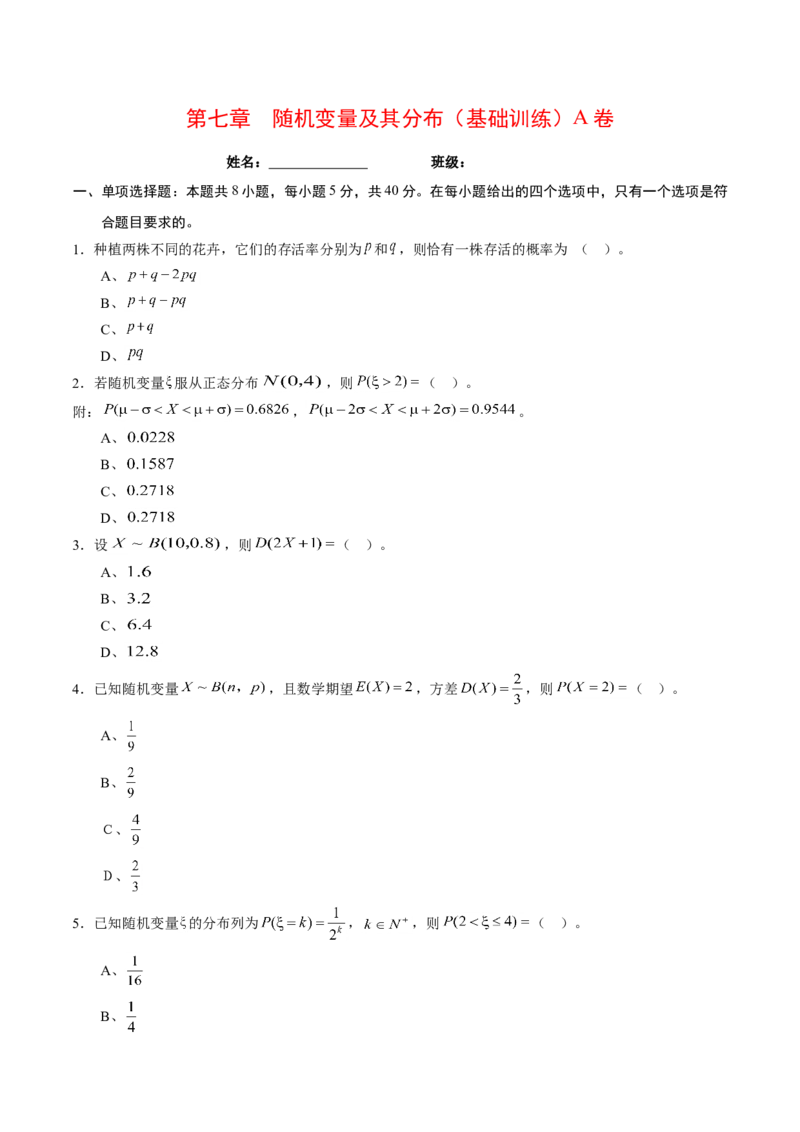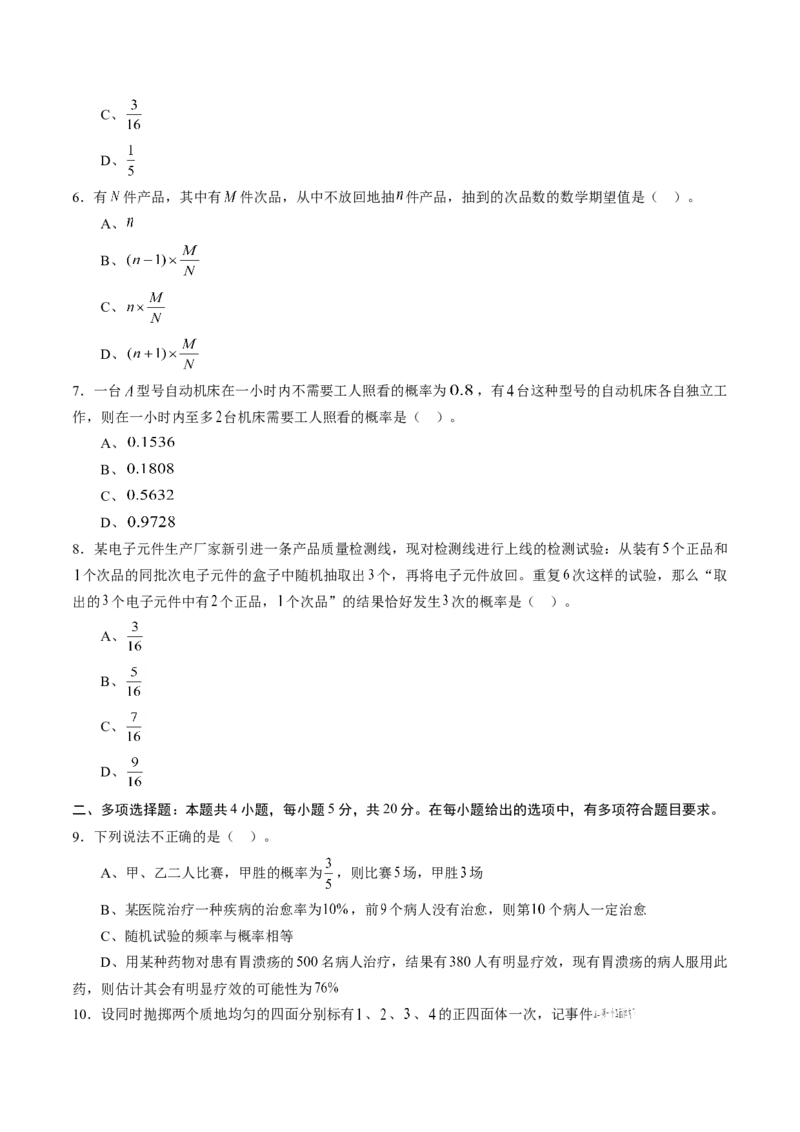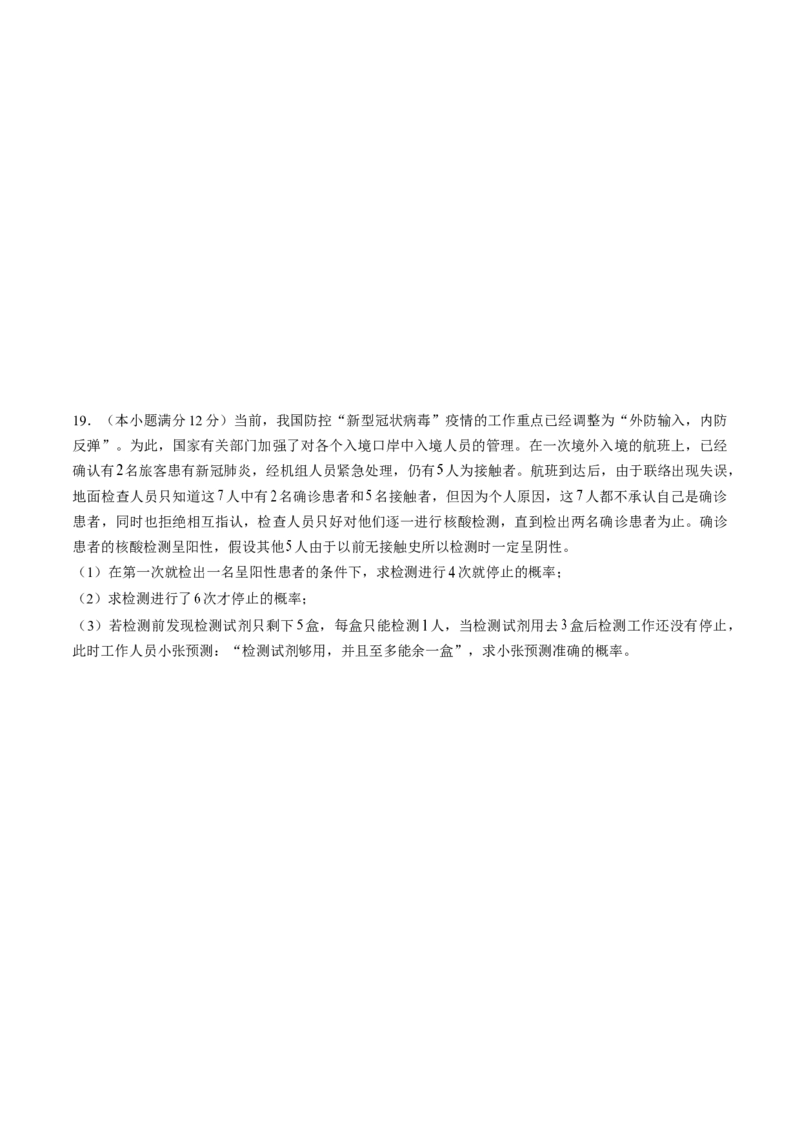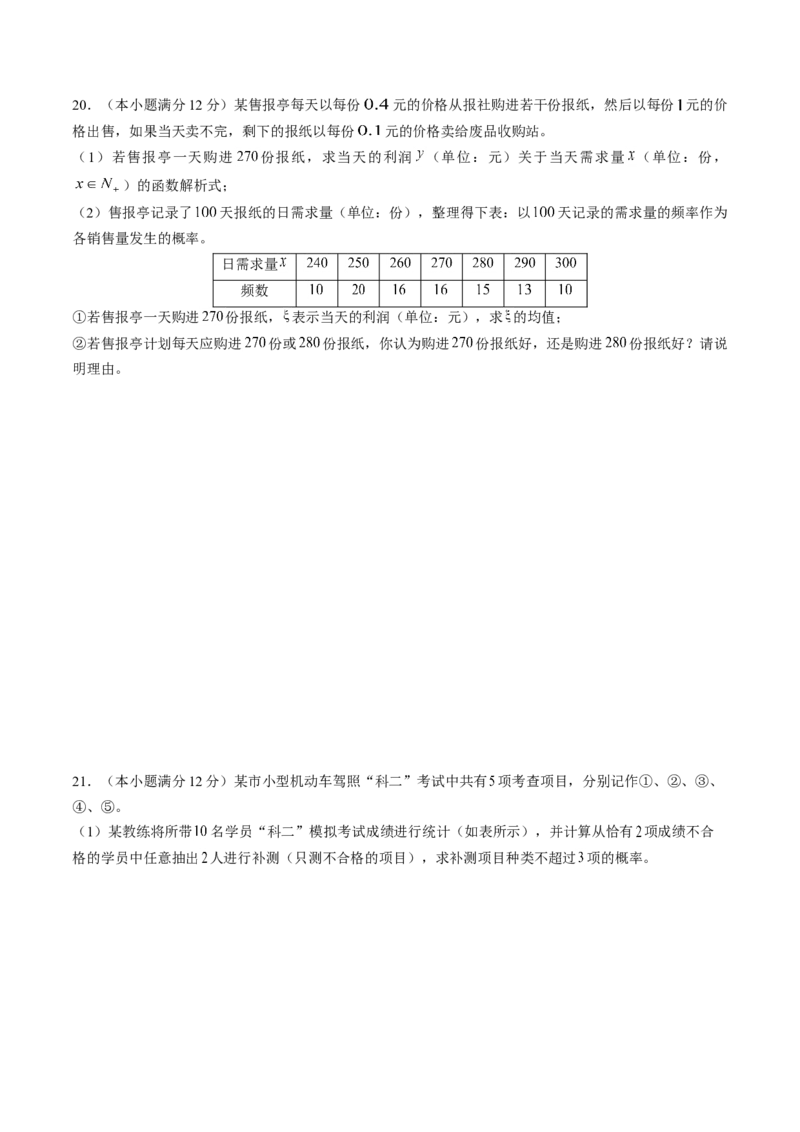文档内容
第七章 随机变量及其分布(基础训练)A 卷
姓名: 班级:
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一个选项是符
合题目要求的。
1.种植两株不同的花卉,它们的存活率分别为 和 ,则恰有一株存活的概率为 ( )。
A、
B、
C、
D、
2.若随机变量 服从正态分布 ,则 ( )。
附: , 。
A、
B、
C、
D、
3.设 ,则 ( )。
A、
B、
C、
D、
4.已知随机变量 ,且数学期望 ,方差 ,则 ( )。
A、
B、
C、
D、
5.已知随机变量 的分布列为 , ,则 ( )。
A、
B、C、
D、
6.有 件产品,其中有 件次品,从中不放回地抽 件产品,抽到的次品数的数学期望值是( )。
A、
B、
C、
D、
7.一台 型号自动机床在一小时内不需要工人照看的概率为 ,有 台这种型号的自动机床各自独立工
作,则在一小时内至多 台机床需要工人照看的概率是( )。
A、
B、
C、
D、
8.某电子元件生产厂家新引进一条产品质量检测线,现对检测线进行上线的检测试验:从装有 个正品和
个次品的同批次电子元件的盒子中随机抽取出 个,再将电子元件放回。重复 次这样的试验,那么“取
出的 个电子元件中有 个正品, 个次品”的结果恰好发生 次的概率是( )。
A、
B、
C、
D、
二、多项选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法不正确的是( )。
A、甲、乙二人比赛,甲胜的概率为 ,则比赛 场,甲胜 场
B、某医院治疗一种疾病的治愈率为 ,前 个病人没有治愈,则第 个病人一定治愈
C、随机试验的频率与概率相等
D、用某种药物对患有胃溃疡的 名病人治疗,结果有 人有明显疗效,现有胃溃疡的病人服用此
药,则估计其会有明显疗效的可能性为
10.设同时抛掷两个质地均匀的四面分别标有 、 、 、 的正四面体一次,记事件,事件 ,事件
,则下列说法正确的是( )。
A、
B、
C、
D、
11.红外线自动测温门能有效避免测温者与被测温者近距离接触,从而降低了潜在的感染风险,为防控新
冠肺炎,某厂家生产了一批红外线自动测温门,其测量体温误差服从正态分布,设 表示其体温误差,且
,则下列结论正确的是( )。
( 附 : 若 随 机 变 量 , 则 ,
)
A、 、
B、
C、
D、
12.骰子通常作为桌上游戏的小道具,最常见的骰子是六面骰,它是一个质地均匀的正方体,六个面上分
别写有数字 、 、 、 、 、 ,现有一款闯关游戏,共有 关,规则如下:在第 关要抛掷六面骰 次,
每次观察向上面的点数并做记录,如果这 次抛掷所出现的点数之和大于 ,则算闯过第 关, 、
、 、 ,假定每次闯关互不影响,则( )。
A、直接挑战第 关并过关的概率为
B、连续挑战前两关并过关的概率为
C、若直接挑战第三关,设 “三个点数之和等于 ”, “至少出现一个 点”,则
D、若直接挑战第 关,则过关的概率是
三、填空题:本题共4小题,每小题5分,共20分。
13.已知随机变量 ,则 。
14.某飞碟运动员每次射击中靶的概率为 ,该运动员连续 次射击,中靶 次的概率是 。
15.由数字 、 、 、 、 、 组成没有重复数字的四位数,定义个位数字比十位数字大、千位数字是偶数、百位数字为奇数的没有重复数字的四位数为“特征数”。从组成的所有没有重复数字的四位数中任取
一个,则这个四位数是“特征数”的概率为 。
16.袋中装有 个大小相同的球,其中 个白球、 个黑球、 个红球。现从中依次取球,每次取 球,且
取后不放回,直到取出的球中有两种不同颜色的球时结束。用 表示终止取球时已取球的次数,则随机变
量 的数学期望 。
四、解答题:本题共6小题,共70分。应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)已知 个乒乓球,其中 个新的, 个旧的,每次取 个,不放回的取两次,求:
(1)第一次取到新球的概率;
(2)第二次取到新球的概率;
(3)在第一次取到新球的条件下第二次取到新球的概率。
18.(本小题满分12分)为发展业务,某调研组对 、 两个公司的产品需求量进行调研,准备从国内
个人口超过 万的超级大城市和 个人口低于 万的小城市中随机抽取若干个城市进行统计。若一次
抽取 个城市,每个城市抽取的可能性均相等。
(1)假设取出小城市的个数为 ,求 的分布列及数学期望 ;
(2)若取出的 个城市是同一类城市,求全为超大城市的概率。19.(本小题满分12分)当前,我国防控“新型冠状病毒”疫情的工作重点已经调整为“外防输入,内防
反弹”。为此,国家有关部门加强了对各个入境口岸中入境人员的管理。在一次境外入境的航班上,已经
确认有 名旅客患有新冠肺炎,经机组人员紧急处理,仍有 人为接触者。航班到达后,由于联络出现失误,
地面检查人员只知道这 人中有 名确诊患者和 名接触者,但因为个人原因,这 人都不承认自己是确诊
患者,同时也拒绝相互指认,检查人员只好对他们逐一进行核酸检测,直到检出两名确诊患者为止。确诊
患者的核酸检测呈阳性,假设其他 人由于以前无接触史所以检测时一定呈阴性。
(1)在第一次就检出一名呈阳性患者的条件下,求检测进行 次就停止的概率;
(2)求检测进行了 次才停止的概率;
(3)若检测前发现检测试剂只剩下 盒,每盒只能检测 人,当检测试剂用去 盒后检测工作还没有停止,
此时工作人员小张预测:“检测试剂够用,并且至多能余一盒”,求小张预测准确的概率。20.(本小题满分12分)某售报亭每天以每份 元的价格从报社购进若干份报纸,然后以每份 元的价
格出售,如果当天卖不完,剩下的报纸以每份 元的价格卖给废品收购站。
(1)若售报亭一天购进 份报纸,求当天的利润 (单位:元)关于当天需求量 (单位:份,
)的函数解析式;
(2)售报亭记录了 天报纸的日需求量(单位:份),整理得下表:以 天记录的需求量的频率作为
各销售量发生的概率。
日需求量
频数
①若售报亭一天购进 份报纸, 表示当天的利润(单位:元),求 的均值;
②若售报亭计划每天应购进 份或 份报纸,你认为购进 份报纸好,还是购进 份报纸好?请说
明理由。
21.(本小题满分12分)某市小型机动车驾照“科二”考试中共有 项考查项目,分别记作①、②、③、
④、⑤。
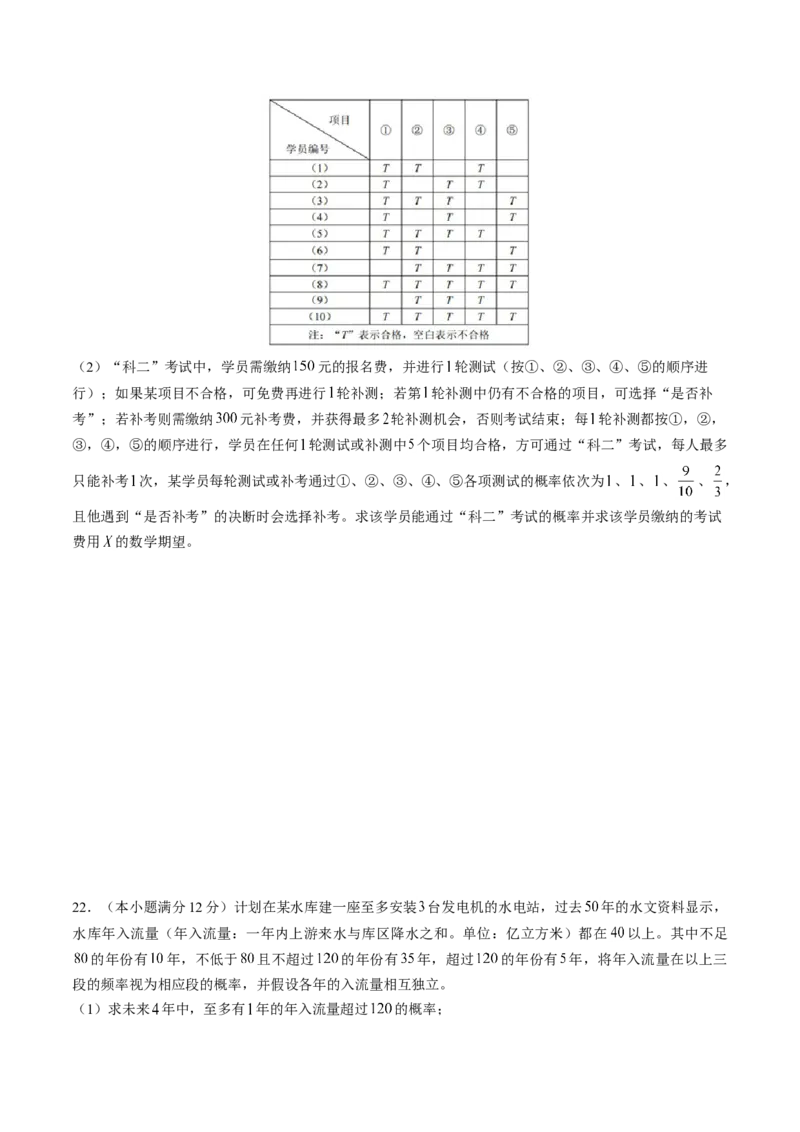
(1)某教练将所带 名学员“科二”模拟考试成绩进行统计(如表所示),并计算从恰有 项成绩不合
格的学员中任意抽出 人进行补测(只测不合格的项目),求补测项目种类不超过 项的概率。(2)“科二”考试中,学员需缴纳 元的报名费,并进行 轮测试(按①、②、③、④、⑤的顺序进
行);如果某项目不合格,可免费再进行 轮补测;若第 轮补测中仍有不合格的项目,可选择“是否补
考”;若补考则需缴纳 元补考费,并获得最多 轮补测机会,否则考试结束;每 轮补测都按①,②,
③,④,⑤的顺序进行,学员在任何 轮测试或补测中 个项目均合格,方可通过“科二”考试,每人最多
只能补考 次,某学员每轮测试或补考通过①、②、③、④、⑤各项测试的概率依次为 、 、 、 、 ,
且他遇到“是否补考”的决断时会选择补考。求该学员能通过“科二”考试的概率并求该学员缴纳的考试
费用 的数学期望。
22.(本小题满分12分)计划在某水库建一座至多安装 台发电机的水电站,过去 年的水文资料显示,
水库年入流量(年入流量:一年内上游来水与库区降水之和。单位:亿立方米)都在 以上。其中不足
的年份有 年,不低于 且不超过 的年份有 年,超过 的年份有 年,将年入流量在以上三
段的频率视为相应段的概率,并假设各年的入流量相互独立。
(1)求未来 年中,至多有 年的年入流量超过 的概率;(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量 限制,并有如下
关系:
年入流量
发电机最多可运行台数
若某台发电机运行,则该台发电机年利润为 万元。若某台发电机为运行,则该台发电机年亏损 万
元。欲使水电站年总利润的均值达到最大,应安发电机多少台?