文档内容
学年度第一学期期末教学质量检测
2023—2024
高三数学试题
注意事项: 审题人 莘县实高 李存才 罗增交
:
答题前 考生务必用 毫米黑色签字笔将自己的姓名 座号 考生号 县区和科类填写
1. , 0.5 、 、 、
到答题卡和试卷规定的位置上
.
第 卷每小题选出答案后 用 铅笔把答题卡上对应题目的答案标号涂黑 如需改动
2. Ⅰ , 2B ; ,
用橡皮擦干净后 再选涂其他答案标号
, .
第 卷必须用 毫米黑色签字笔作答 答案必须写在答题卡各题目指定区域内相应的
3. Ⅱ 0.5 ,
位置 如需改动 先划掉原来的答案 然后再写上新的答案 不能使用涂改液 胶带纸 修正带 不
; , , ; 、 、 .
按以上要求作答的答案无效
.
一、单项选择题:本题共 小题,每小题 分,共 分 在每小题给出的四个选项中,只有一项是
8 5 40 .
符合题目要求的
.
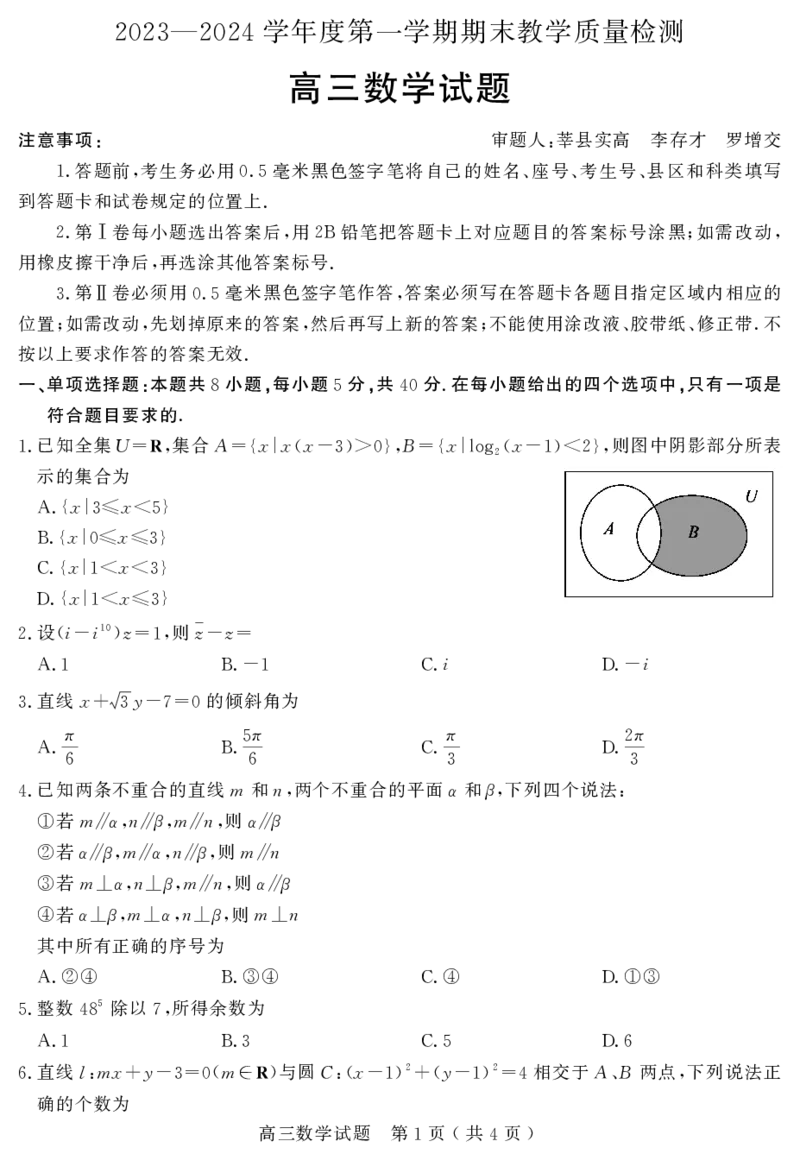
已知全集U R 集合A xxx B x x 则图中阴影部分所表
1. = , ={| ( -3)>0}, ={|log2( -1)<2},
示的集合为
x x
A.{|3≤ <5}
x x
B.{|0≤ ≤3}
x x
C.{|1< <3}
x x
D.{|1< ≤3}
2
.设
(
i
-
i10
)
z
=1,
则z
-
z
=
i i
A.1 B.-1 C. D.-
.直线x y 的倾斜角为
3 + 3 -7=0
π π π π
5 2
A. B. C. D.
6 6 3 3
.已知两条不重合的直线m和n 两个不重合的平面α和
β
下列四个说法
4 , , :
若m αnβm n 则αβ
① ∥ ,∥ , ∥ , ∥
若αβm αnβ 则m n
② ∥ , ∥ ,∥ , ∥
若m αn βm n 则αβ
③ ⊥ ,⊥ , ∥ , ∥
若α βm αn β 则m n
④ ⊥ , ⊥ ,⊥ , ⊥
其中所有正确的序号为
A.②④ B.③④ C.④ D.①③
整数 除以 所得余数为
5
5. 48 7,
A.1 B.3 C.5 D.6
直线lmx y m R 与圆C x 2 y 2 相交于AB两点 下列说法正
6. : + -3=0( ∈ ) : -1 + -1 =4 、 ,
确的个数为
高三数学试题 第 页 共 页
1 ( 4 )
{#{QQABDQSQggAoAAAAAQhCEwGoCgAQkACACAoGgAAIsAAAiQFABAA=}#}直线l过定点
① (0,3)
m 时 弦AB最长
② =2 ,
m 时 ABC为等腰直角三角形
③ =1 ,△
m 3时 弦AB长为
④ = , 23
4
A.3 B.2 C.1 D.4
最优化原理是指要求目前存在的多种可能的方案中 选出最合理的 达到事先规定的最优目标
7. , ,
的方案 这类问题称之为最优化问题 为了解决实际生活中的最优化问题 我们常常需要在数学
, . ,
模型中求最大值或者最小值 下面是一个有关曲线与直线上点的距离的最值问题 请你利用所
. ,
学知识来解答 若点M是曲线y 3x2 x上任意一点 则M到直线x y 的距离的
: = -2ln , - -2=0
2
最小值为
52 52 32 32
A. B. C. D.
2 4 4 2
8. 设等差数列 a n 的前n项和为S n, 已知 :( a 12-1) 3 +2023( a 12-1)=1,
a 3 a 则下列结论正确的是
(2012-1)+2023(2012-1)=-1,
S a a S a a
A.2023=-2023,2012< 12 B.2023=2023,2012> 12
S a a S a a
C.2023=-2023,2012> 12 D.2023=2023,2012< 12
二、多项选择题:本题共 小题,每小题 分,共 分.在每小题给出的四个选项中,有多项符合
4 5 20
题目要求.全部选对的得 分,部分选对的得 分,有选错的得 分.
5 2 0
.尊重自然 顺应自然 保护环境 是全面建设社会主义现代化国家的内在要求 近年来 各地区
9 、 、 , , ,
以一系列卓有成效的有力措施逐步改善生态环境 我国生态文明建设发生了历史性 全局性
, 、
的变化.一地区的科研部门调查某绿色植被培育的株高X 单位 的情况 得出X N
( :cm) , ~
则下列说法正确的是
2
100,10 ,
该地植被株高的均值为
A. 100
该地植被株高的方差为
B. 10
若PX m PX m 则m
C. ( > )= ( <2 -7), =69
随机测量一株植被 其株高在 以上的概率与株高在 以下的概率一样
D. , 120cm 70cm
已知ω 函数fx ωx ωx 2ωx 3的最小正周期为 π
10. >0, =sin cos + 3cos - 2 ,
2
则下列结论正确的是
ω
A.=1
π π
函数fx 在区间 上单调递增
B. [- , ]
1212
π
将函数fx 的图象向左平移 个单位长度可得函数gx x的图象
C. ()=cos
6
π
函数fx 的图象关于直线x 对称
D. =
12
高三数学试题 第 页 共 页
2 ( 4 )
{#{QQABDQSQggAoAAAAAQhCEwGoCgAQkACACAoGgAAIsAAAiQFABAA=}#}.下列说法中正确的是
11
函数y x 4 的最小值为
A. =sin + x 4
sin
若a b 则 a b的最小值为
B. + =2, 2+2 4
若a b a b ab 则ab的最大值为
C. >0,>0,+ + =3, 1
若x y 且满足x y 则1 4的最小值为9
D. >0,>0, + =2, x+y
2
.正方体ABCD ABCD 的棱长为 P为侧面AADD上的点 Q为侧面CCDD上
12 - 1 1 1 1 1, 1 1 , 1 1
的点 则下列判断正确的是
,
直线AC 平面ABD
A. 1⊥ 1
若BQ AC 则Q CD 且直线BQ 平面ABD
B. 1 ⊥ 1, ∈ 1, 1 ∥ 1
若BP 5 则P到直线AD的距离的最小值为 2
C. = , 1
2 4
若P AD 则BP与平面ABD所成角正弦的最小值为 3
D. ∈ 1 , 1 1
3
三、填空题:本题共 个小题,每小题 分,共 分.
4 5 20
.已知向量a t b t 若a与b所成的角为钝角 则实数t的取值范围 .
13 =(3+1,2),=(1,), , :
.每年 月第三个星期六是我国法定的全民国防教育日 同学们积极参与到国防教育之中为
14 9 ,
实现中国梦 强军梦凝聚强大力量.某校国防教育活动中拟将 本不同的国防知识书分给
、 7
甲 乙 丙三个班 其中一个班得 本 另外两个班每班得 本 则共有 种不同的分配
、 、 , 3 , 2 ;
方式.请用数字作答
( )
a x ax fx fx
.函数fx (-3)+4 (≤1)满足对任意x x 都有 1 - 2 成立 则实
15 ()= xx 1≠ 2, x x <0 ,
log a (>1) 1- 2
数a的取值范围是 .
x2
.椭圆C y2 的左右焦点分别为F F O为坐标原点 给出以下四个命题
16 : + =1 1,2, , :
9
过点F 的直线与椭圆C交于AB两点 则 ABF 的周长为
① 2 , , △ 1 12;
椭圆C上存在点P 使得PF→ PF→
② , 1· 2=0;
椭圆C的离心率为1
③ ;
3
x2
P为椭圆C y2 上一点 Q为圆x2 y2 上一点 则点PQ的最大距离为 .
④ : + =1 , + =1 , , 4
9
其中正确的序号有 .
四、解答题:本题共 小题,共 分.解答应写出文字说明,证明过程或演算步骤.
6 70
.本小题满分 分
17 ( 10 )
记 ABC的内角ABC的对边分别为abc已知 C B c b a A B .
△ ,, ,,, sin +sin - = sin -sin
求角C的大小
(1)
设c CA→ CB→ 求ΔABC的周长.
(2) =3, · =1,
高三数学试题 第 页 共 页
3 ( 4 )
{#{QQABDQSQggAoAAAAAQhCEwGoCgAQkACACAoGgAAIsAAAiQFABAA=}#}.本小题满分 分
18 ( 12 )
已知等差数列 a
n
的前n项和为S
n,
且a
2=4,
S
8=72,
n
∈
N*.
求数列a 的通项公式
(1) n ;
记数列 1 的前n项和T 求证 T 11.
(2) S a n, :n<
n+ n 18
.本小题满分 分
19 ( 12 )
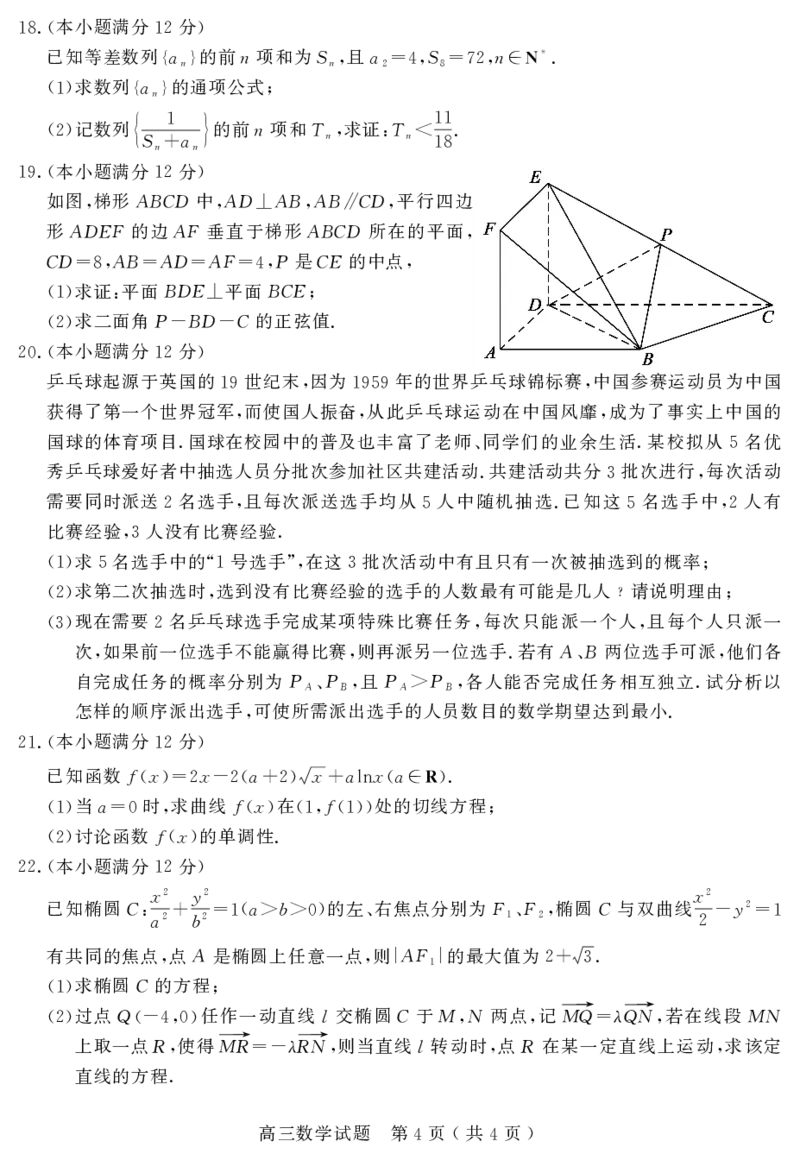
如图 梯形ABCD中 AD ABAB CD 平行四边
, , ⊥ , ∥ ,
形ADEF的边AF垂直于梯形ABCD所在的平面
,
CD AB AD AF P是CE的中点
=8, = = =4, ,
求证 平面BDE 平面BCE
(1) : ⊥ ;
求二面角P BD C的正弦值.
(2) - -
.本小题满分 分
20 ( 12 )
乒乓球起源于英国的 世纪末 因为 年的世界乒乓球锦标赛 中国参赛运动员为中国
19 , 1959 ,
获得了第一个世界冠军 而使国人振奋 从此乒乓球运动在中国风靡 成为了事实上中国的
, , ,
国球的体育项目.国球在校园中的普及也丰富了老师 同学们的业余生活.某校拟从 名优
、 5
秀乒乓球爱好者中抽选人员分批次参加社区共建活动.共建活动共分 批次进行 每次活动
3 ,
需要同时派送 名选手 且每次派送选手均从 人中随机抽选.已知这 名选手中 人有
2 , 5 5 ,2
比赛经验 人没有比赛经验.
,3
求 名选手中的 号选手 在这 批次活动中有且只有一次被抽选到的概率﹔
(1) 5 “1 ”, 3
求第二次抽选时 选到没有比赛经验的选手的人数最有可能是几人﹖请说明理由
(2) , ;
现在需要 名乒乓球选手完成某项特殊比赛任务 每次只能派一个人 且每个人只派一
(3) 2 , ,
次 如果前一位选手不能赢得比赛 则再派另一位选手.若有AB两位选手可派 他们各
, , 、 ,
自完成任务的概率分别为P P 且P P 各人能否完成任务相互独立.试分析以
A、B, A> B,
怎样的顺序派出选手 可使所需派出选手的人员数目的数学期望达到最小.
,
.本小题满分 分
21 ( 12 )
已知函数fx x a x a xa R .
()=2 -2(+2) + ln (∈ )
当a 时 求曲线fx 在 f 处的切线方程
(1) =0 , () (1,(1)) ;
讨论函数fx 的单调性.
(2) ()
.本小题满分 分
22 ( 12 )
x2 y2 x2
已知椭圆C a b 的左 右焦点分别为F F 椭圆C与双曲线 y2
:a2+b2=1(> >0) 、 1、2, - =1
2
有共同的焦点 点A是椭圆上任意一点 则 AF 的最大值为 .
, , | 1| 2+ 3
求椭圆C的方程
(1) ;
过点Q 任作一动直线l交椭圆C于M N 两点 记MQ→ λQN→ 若在线段MN
(2) -4,0 , , = ,
上取一点R 使得MR→ λRN→ 则当直线l转动时 点R在某一定直线上运动 求该定
, =- , , ,
直线的方程.
高三数学试题 第 页 共 页
4 ( 4 )
{#{QQABDQSQggAoAAAAAQhCEwGoCgAQkACACAoGgAAIsAAAiQFABAA=}#}学年度第一学期期末教学质量检测
2023—2024
高三数学试题参考答案
一 单项选择题 本题共 小题 每小题 分 共 分.在每小题给出的四个选项中 只有一项是
、 : 8 , 5 , 40 ,
符合题目要求的.
二 多项选择题 本题共 小题 每小题 分 共 分.在每小题给出的四个选项中 有多项符合
、 : 4 , 5 , 20 ,
题目要求.全部选对的得 分 部分选对的得 分 有选错的得 分.
5 , 2 , 0
题 号
1 2 3 4 5 6 7 8 9 10 11 12
答 案
D C B B D A B D AC BC BCD AB
解析 函数fx x3 x是R上的奇函数 且单调递增
8. : ()= +2023 , ,
由题意fa fa
:(12-1)=1,(2012-1)=-1
两式相加得fa fa
:(12-1)+ (2012-1)=0
fx 是R上的奇函数fa fa f a
∵ () ,(12-1)=- (2012-1)= (1- 2012)
fx 在R上单调递增a a a a
∵ () 12-1=1- 2012,12+ 2012=2
等差数列a 的前n项和为S .
∵ n n
Sn 2023a a 2023a a
= (1+ 2023)= (12+ 2012)=2023
2 2
fa fa fa fa
∵ (12-1)=1,(2012-1)=-1,(12-1)> (2012-1)
fx 在R上单调递增a a 即a a 故选
∵ () 12-1> 2012-1, 12> 2012, D.
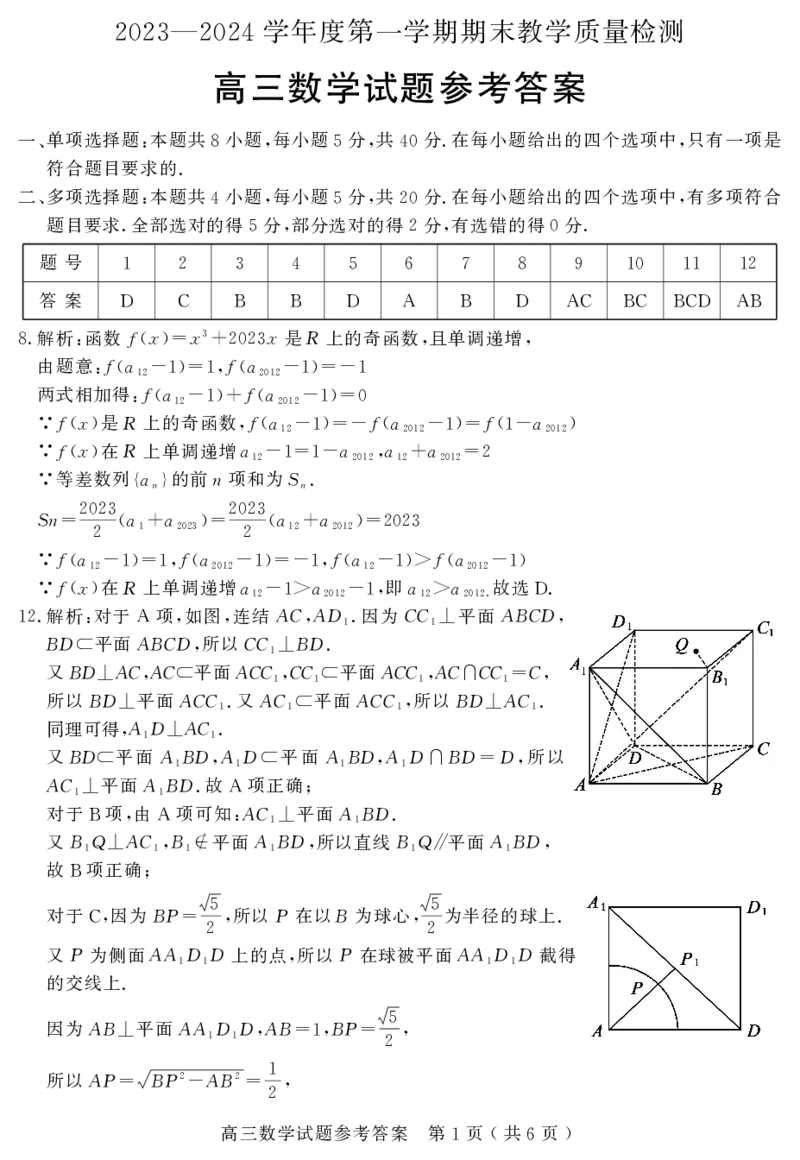
解析 对于 项 如图 连结ACAD .因为CC 平面ABCD
12. : A , , , 1 1⊥ ,
BD 平面ABCD 所以CC BD.
⊂ , 1⊥
又BD ACAC 平面ACC CC 平面ACC AC CC C
⊥ , ⊂ 1, 1⊂ 1, ∩ 1= ,
所以BD 平面ACC .又AC 平面ACC 所以BD AC .
⊥ 1 1⊂ 1, ⊥ 1
同理可得AD AC.
,1 ⊥ 1
又BD 平面ABDAD 平面ABDAD BD D 所以
⊂ 1 , 1 ⊂ 1 , 1 ∩ = ,
AC 平面ABD.故 项正确
1⊥ 1 A ;
对于 项 由 项可知 AC 平面ABD.
B , A : 1⊥ 1
又BQ AC B 平面ABD 所以直线BQ 平面ABD
1 ⊥ 1,1∉ 1 , 1 ∥ 1 ,
故 项正确
B ;
对于 因为BP 5 所以P在以B为球心 5为半径的球上.
C, = , ,
2 2
又P为侧面AADD上的点 所以P在球被平面AADD截得
1 1 , 1 1
的交线上.
因为AB 平面AADDAB BP 5
⊥ 1 1 , =1, = ,
2
所以AP BP2 AB2 1
= - = ,
2
高三数学试题参考答案 第 页 共 页
1 ( 6 )
{#{QQABDQSQggAoAAAAAQhCEwGoCgAQkACACAoGgAAIsAAAiQFABAA=}#}所以P为以A点为圆心 1为半径的圆上.如图 AP AD
, , 1⊥ 1 ,
2
则AP 2P到直线AD的距离的最小值为 2 1 故 项错误
1= , 1 - , C ;
2 2 2
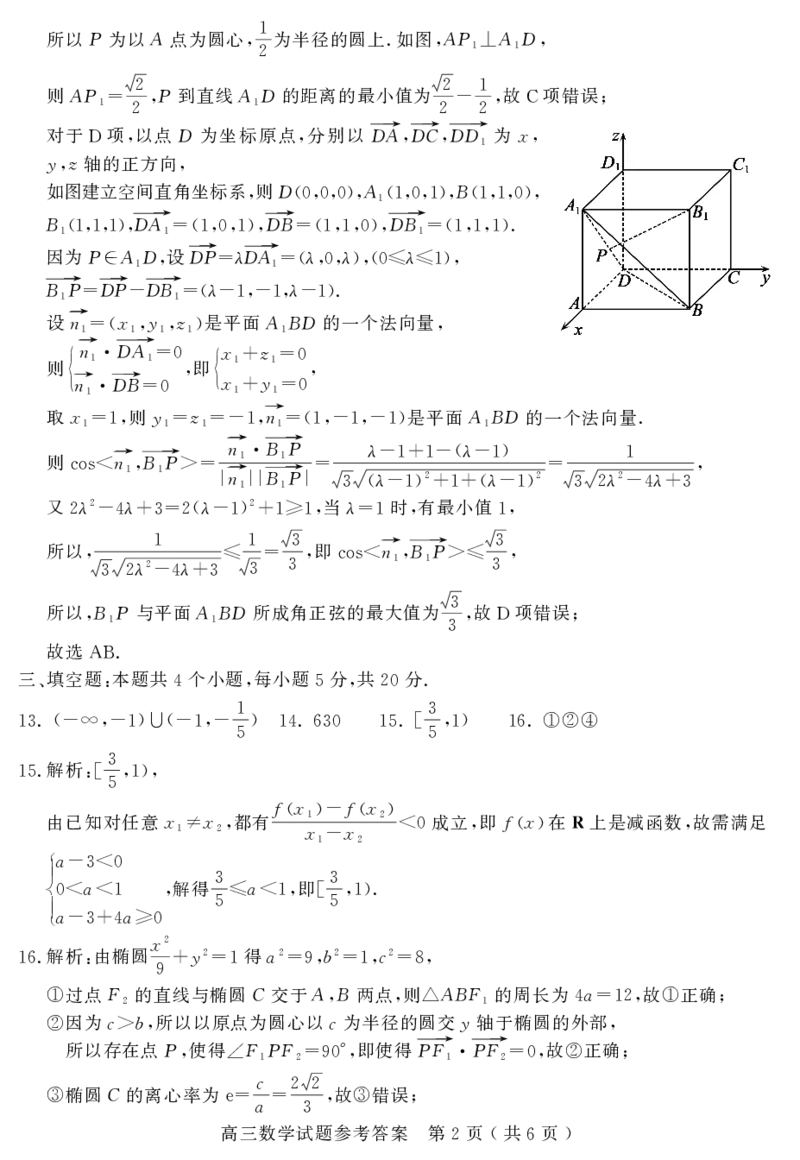
对于 项 以点D为坐标原点 分别以DA→ DC→ DD→ 为x
D , , , , 1 ,
yz轴的正方向
, ,
如图建立空间直角坐标系 则D A B
, (0,0,0),1(1,0,1), (1,1,0),
B DA→ DB→ DB→ .
1(1,1,1), 1=(1,0,1), =(1,1,0), 1=(1,1,1)
因为P AD 设DP→ λDA→ λ λ λ
∈ 1 , = 1=(,0,),(0≤ ≤1),
BP→ DP→ DB→ λ λ .
1 = - 1=(-1,-1,-1)
设n→ x y z 是平面ABD的一个法向量
1=(1,1,1) 1 ,
n→ DA→ x z
则 1· 1=0 即 1+ 1=0
n→ DB→ , x y ,
1· =0 1+ 1=0
取x 则y z n→ 是平面ABD的一个法向量.
1=1, 1= 1=-1,1=(1,-1,-1) 1
n→ BP→ λ λ
则 n→BP→ 1· 1 -1+1-(-1) 1
cos< 1,1 >=n→ BP→ = λ 2 λ 2 = λ2 λ ,
| 1|| 1 | 3 (-1)+1+(-1) 3 2 -4 +3
又 λ2 λ λ 2 当λ 时 有最小值
2 -4 +3=2(-1)+1≥1, =1 , 1,
所以 1 1 3 即 n→BP→ 3
,
3 2
λ2
-4
λ
+3
≤
3
=
3
, cos< 1,1 >≤
3
,
所以 BP与平面ABD所成角正弦的最大值为 3 故 项错误
,1 1 , D ;
3
故选
AB.
三 填空题 本题共 个小题 每小题 分 共 分
、 : 4 , 5 , 20 .
1 3
13.(-∞,-1)∪(-1,- ) 14.630 15.[ ,1) 16.①②④
5 5
.解析 3
15 :[ ,1),
5
fx fx
由已知对任意x x 都有 1 - 2 成立 即fx 在R上是减函数 故需满足
1≠ 2, x x <0 , ,
1- 2
a
-3<0
a
0< <1
a a
-3+4 ≥0
解得3 a 即 3 .
, ≤ <1, [ ,1)
5 5
x2
.解析 由椭圆 y2 得a2 b2 c2
16 : + =1 =9, =1, =8,
9
过点F 的直线与椭圆C交于AB两点 则 ABF 的周长为 a 故 正确
① 2 , , △ 1 4 =12, ① ;
因为c b 所以以原点为圆心以c为半径的圆交y轴于椭圆的外部
② > , ,
所以存在点P 使得 FPF ° 即使得PF→ PF→ 故 正确
, ∠ 1 2=90, 1· 2=0, ② ;
c
椭圆C的离心率为 22 故 错误
③ e=a= , ③ ;
3
高三数学试题参考答案 第 页 共 页
2 ( 6 )
{#{QQABDQSQggAoAAAAAQhCEwGoCgAQkACACAoGgAAIsAAAiQFABAA=}#}x2
因为P为椭圆 y2 上一点 设P α α α π
④ + =1 , (3cos ,sin ),∈[0,2 ),
9
则点P到圆心 的距离为d a2 a2 2a
(0,0) = (3cos )+sin = 1+8cos
则其最大值为 所以 PQ 最大值为 故 正确
3, | | :3+1=4, ④ ;
故填 .
①②④
四 解答题 本题共 小题 共 分.解答应写出文字说明 证明过程或演算步骤.
、 : 6 , 70 ,
.本小题满分 分
17 ( 10 )
解 由 C B c b a A B 及正弦定理
:(1) (sin +sin )(- )= (sin -sin ) ,
得c b c b aa b 即a2 b2 c2 ab 分
(+ )(- )= (- ), + - = , ……………………………………… 2
a2 b2 c2
所以 C + - 1. 分
cos = ab = ……………………………………………………………… 4
2 2
π
因为C π 所以C . 分
∈(0,), = ……………………………………………………………… 5
3
CA→ CB→ ab C ab 分
(2)∵ · =1,∴ cos =1,∴ =2 ……………………………………………… 7
c2 a2 b2 ab C a b2 ab ab a b 分
∵ = + -2 cos ,∴9=(+ )-2 - ,∴ + = 15,…………………… 9
ΔABC的周长为 . 分
∴ 3+ 15 ……………………………………………………………… 10
.本小题满分 分
18 ( 12 )
解 设等差数列a 的公差为d
:(1) n ,
a d
a 1+ =4
2=4
∵S ∴a 8×7d
8=72 8 1+ =72
2
a
解得 1=2 分
d …………………………………………… 4
=2
所以a
n=2
n
,
n
∈
N*
……………………………………………………………………… 5
分
n n
(2)
S
n=
2+2
=
n2
+
n
, ……………………………………………………………… 6
分
2
则 1 1 1 1 1 分
S
n+
a
n
=n2
+3
n=
3
n-n
+3
,…………………………………………………… 8
所以T n = 1 1- 1 + 1 - 1 + 1 - 1 + 1 - 1 +…+ n 1 -n 1
3 4 2 5 3 6 4 7 +3
1 1 1 1 1 1 分
= 1+ + -n -n -n ……………………………………… 10
3 2 3 +1 +2 +3
1 1 1 11 分
< 1+ + = ………………………………………………………… 11
3 2 3 18
所以T 11. 分
n< ……………………………………………………………………………… 12
18
.本小题满分 分
19 ( 12 )
解 平行四边形ADEF的边AF垂直于梯形ABCD所在的平面 而AD在平面ABCD内
:(1)∵ , ,
则AD AF 又因为AD AF ADEF为正方形 分
⊥ , = =4∴ ………………………………… 1
AF垂直于梯形ABCD所在的平面 AF ED ED 平面ABCD
∵ , ∥ ,∴ ⊥
BC 平面ABCD ED BC 分
∵ ⊂ ∴ ⊥ ………………………………………………………… 2
在直角梯形ABCD中 AB AD CD
, = =4, =8,
高三数学试题参考答案 第 页 共 页
3 ( 6 )
{#{QQABDQSQggAoAAAAAQhCEwGoCgAQkACACAoGgAAIsAAAiQFABAA=}#}则BC CD AB 2 AD2 2 2 BD
= ( - )+ = 4+4 =42, =42,
在 BCD中 BD2 BC2 CD2 BC BD 分
△ , + = ,∴ ⊥ …………………………………………… 4
DE BD DDE与BD 平面BDE
∵ ∩ = , ⊂ ,
BC 平面BDE 分
∴ ⊥ ………………………………………………………………………… 5
又 BC 面BEC
∵ ⊂
平面BDE 平面BEC 分
∴ ⊥ ………………………………………………………………… 6
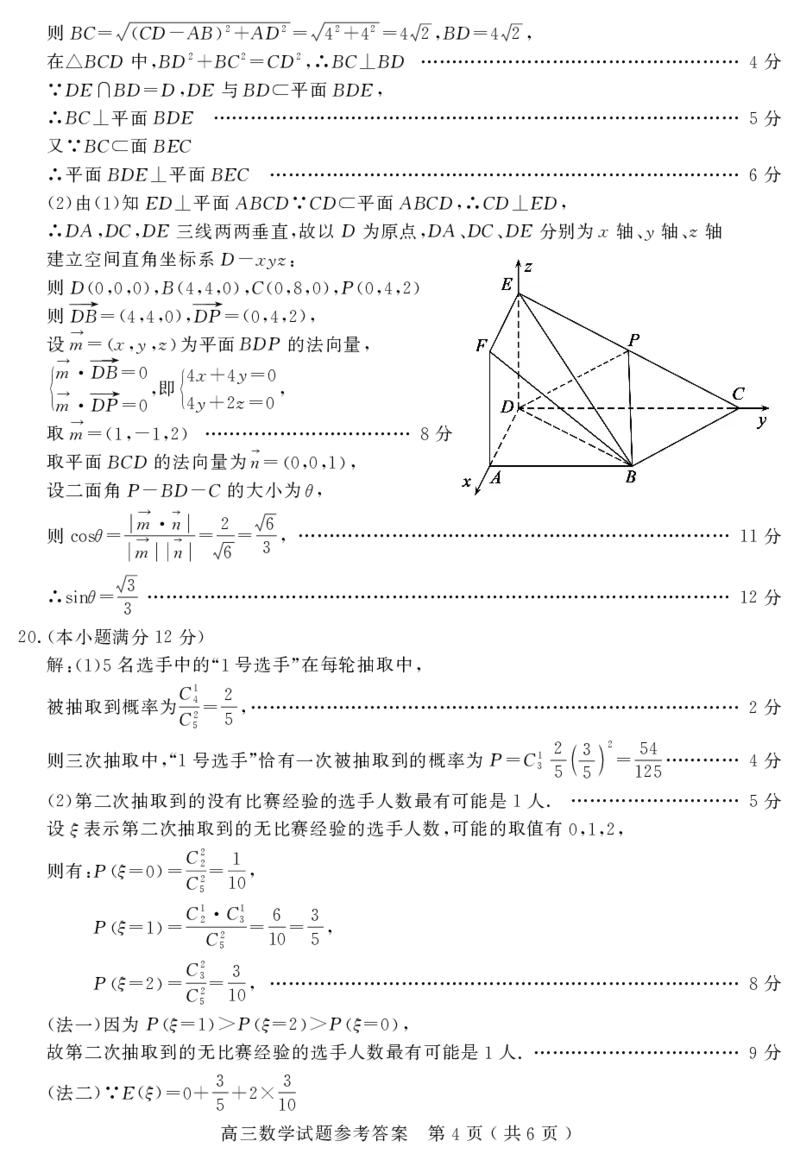
由 知ED 平面ABCD CD 平面ABCD CD ED
(2) (1) ⊥ ∵ ⊂ ,∴ ⊥ ,
DADCDE三线两两垂直 故以D为原点 DADCDE分别为x轴y轴z轴
∴ , , , , 、 、 、 、
建立空间直角坐标系D xyz
- :
则D B C P
(0,0,0), (4,4,0), (0,8,0), (0,4,2)
则DB→ DP→
=(4,4,0), =(0,4,2),
设m xyz 为平面BDP的法向量
= ,, ,
m · DB→
=0 即 4
x
+4
y
=0
m DP→ , y z ,
· =0 4 +2 =0
取m 分
=(1,-1,2) …………………………… 8
取平面BCD的法向量为n
= 0,0,1 ,
设二面角P BD C的大小为θ
- - ,
m n
则 θ · 2 6 分
cos= m n = = ,…………………………………………………………… 11
6 3
θ 3 分
∴sin = ………………………………………………………………………………… 12
3
.本小题满分 分
20 ( 12 )
解 名选手中的 号选手 在每轮抽取中
:(1)5 “1 ” ,
C1
被抽取到概率为 4 2 分
C2= ,…………………………………………………………………… 2
5 5
则三次抽取中 号选手 恰有一次被抽取到的概率为P C1 2 3 2 54 分
,“1 ” = 3 = ………… 4
5 5 125
第二次抽取到的没有比赛经验的选手人数最有可能是 人. 分
(2) 1 ……………………… 5
设 表示第二次抽取到的无比赛经验的选手人数 可能的取值有
ξ
, 0,1,2,
C2
则有 Pξ 2 1
: =0 =C2= ,
5 10
C1 C1
Pξ 2· 3 6 3
=1 = C2 = = ,
5 10 5
C2
Pξ 3 3 分
=2 =C2= ,………………………………………………………………… 8
5 10
法一 因为Pξ Pξ Pξ
( ) =1 > =2 > =0 ,
故第二次抽取到的无比赛经验的选手人数最有可能是 人. 分
1 …………………………… 9
法二 Eξ 3 3
( )∵ ()=0+ +2×
5 10
高三数学试题参考答案 第 页 共 页
4 ( 6 )
{#{QQABDQSQggAoAAAAAQhCEwGoCgAQkACACAoGgAAIsAAAiQFABAA=}#}.
=12
第二次抽取到的无比赛经验的选手人数最有可能是 人. 分
∴ 1 …………………………… 9
按照先A后B的顺序所需人数期望最小.
(3)
由题意 p p
:0< B< A<1
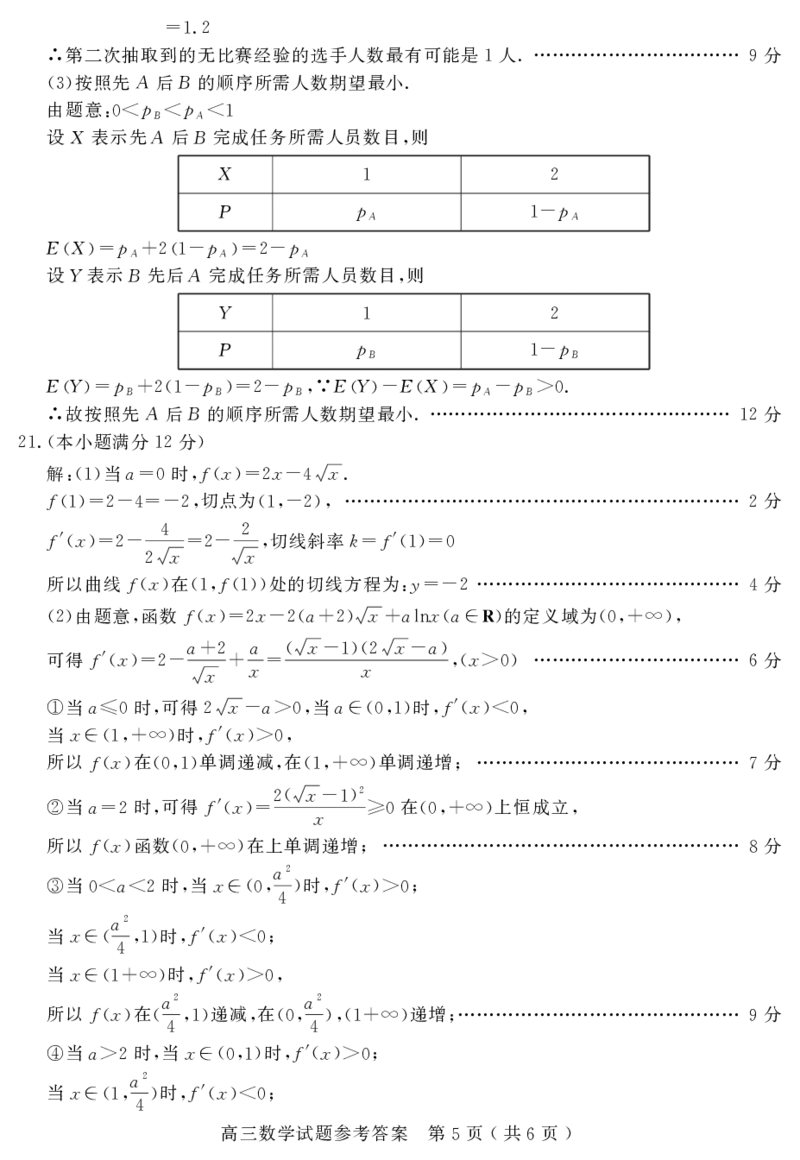
设X表示先A后B完成任务所需人员数目 则
,
X
1 2
P p p
A 1- A
EX p p p
= A+2 1- A =2- A
设Y表示B先后A完成任务所需人员数目 则
,
Y
1 2
P p p
B 1- B
EY p p p EY EX p p .
= B+2(1- B)=2- B,∵ - = A- B>0
故按照先A后B的顺序所需人数期望最小. 分
∴ ………………………………………… 12
.本小题满分 分
21 ( 12 )
解 当a 时fx x x.
:(1) =0 ,()=2 -4
f 切点为 分
(1)=2-4=-2, (1,-2),……………………………………………………… 2
f'x 4 2 切线斜率k f'
()=2- x=2- x , = (1)=0
2
所以曲线fx 在 f 处的切线方程为y 分
() (1,(1)) :=-2…………………………………… 4
由题意 函数fx x a x a xa R 的定义域为
(2) , ()=2 -2(+2) + ln (∈ ) (0,+∞),
a a x x a
可得f'x +2 ( -1)(2 - ) x 分
()=2- x +x= x ,(>0) …………………………… 6
当a 时 可得 x a 当a 时f'x
① ≤0 , 2 - >0, ∈(0,1) , ()<0,
当x 时f'x
∈(1,+∞) , ()>0,
所以fx 在 单调递减 在 单调递增 分
() (0,1) , (1,+∞) ;…………………………………… 7
x 2
当a 时 可得f'x 2( -1) 在 上恒成立
② =2 , ()= x ≥0 (0,+∞) ,
所以fx 函数 在上单调递增 分
() (0,+∞) ;………………………………………………… 8
a2
当 a 时 当x 时f'x
③ 0< <2 , ∈(0, ) , ()>0;
4
a2
当x 时f'x
∈( ,1) , ()<0;
4
当x 时f'x
∈(1+∞) , ()>0,
a2 a2
所以fx 在 递减 在 递增 分
() ( ,1) , (0, ),(1+∞) ;……………………………………… 9
4 4
当a 时 当x 时f'x
④ >2 , ∈(0,1) , ()>0;
a2
当x 时f'x
∈(1, ) , ()<0;
4
高三数学试题参考答案 第 页 共 页
5 ( 6 )
{#{QQABDQSQggAoAAAAAQhCEwGoCgAQkACACAoGgAAIsAAAiQFABAA=}#}a2
当x 时f'x
∈( ,+∞) , ()>0,
4
a2 a2
所以fx 在 递减 在 递增. 分
() (1, ) , (0,1),( ,+∞) …………………………………… 10
4 4
综上 当a 时fx 在 递减 在 递增
, ≤0 ,() (0,1) , (1,+∞) ;
当a 时fx 在 上单调递增
=2 ,() (0,+∞) ;
a2 a2
当 a 时fx 在 递减 在 递增
0< <2 ,() ( ,1) , (0, ),(1,+∞) ;
4 4
a2 a2
当a 时fx 在 递减 在 递增. 分
>2 ,() (1, ) , (0,1),( ,+∞) …………………………… 12
4 4
.本小题满分 分
22 ( 12 )
解 点A是椭圆上任意一点 则 AF 的最大值为 所以a c .
:(1) , | 1| :2+ 3,, + =2+ 3
x2
又与双曲线 –y2 有共同的焦点 所以c
=1 , = 3,
2
x2
所以椭圆C的方程为 y2 . 分
+ =1 …………… 4
4
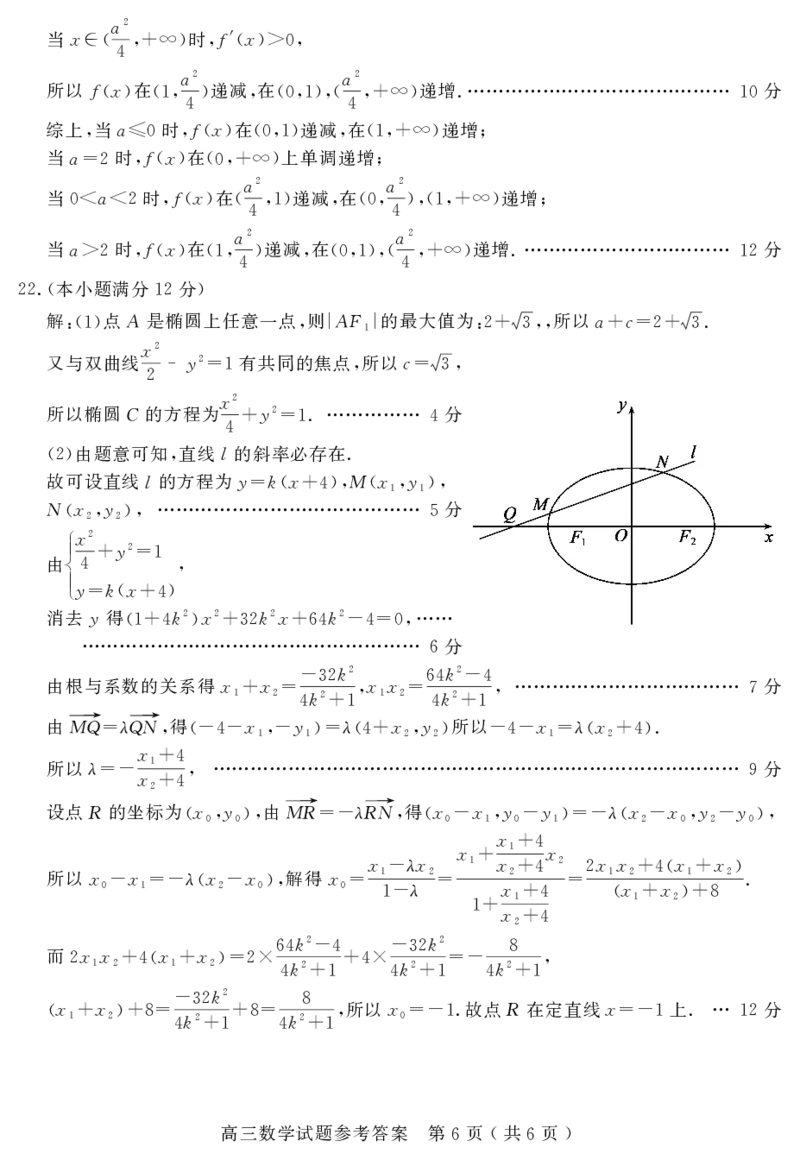
由题意可知 直线l的斜率必存在.
(2) ,
故可设直线l的方程为y kx Mx y
= +4 , 1,1 ,
Nx y 分
2,2 ,…………………………………… 5
x2
y2
由 + =1
4
y kx
= (+4)
,
消去y得 k2 x2 k2x k2
1+4 +32 +64 -4=0,……
分
……………………………………………… 6
k2 k2
由根与系数的关系得x x -32 xx 64 -4 分
1+ 2=k2 ,1 2= k2 ,……………………………… 7
4 +1 4 +1
由MQ→ λQN→ 得 x y λ x y 所以 x λx .
= , -4- 1,- 1 = 4+ 2,2 -4- 1= 2+4
x
所以λ 1+4 分
=-x , ………………………………………………………………………… 9
2+4
设点R的坐标为x y 由MR→ λRN→ 得x x y y λx x y y
0,0 , =- , 0- 1,0- 1 =- 2- 0,2- 0 ,
x
x 1+4x
x λx 1+x 2 xx x x
所以x x λx x 解得x 1- 2 2+4 2 1 2+4 1+ 2 .
0- 1=- 2- 0 , 0= λ = x = x x
1- 1+4 1+ 2 +8
1+x
2+4
k2 k2
而 xx x x 64 -4 -32 8
2 1 2+4 1+ 2 =2× k2 +4×k2 =-k2 ,
4 +1 4 +1 4 +1
k2
x x -32 8 所以x .故点R在定直线x 上. 分
1+ 2 +8=k2 +8=k2 , 0=-1 =-1 … 12
4 +1 4 +1
高三数学试题参考答案 第 页 共 页
6 ( 6 )
{#{QQABDQSQggAoAAAAAQhCEwGoCgAQkACACAoGgAAIsAAAiQFABAA=}#}