文档内容
2024-2025 学年下期高 2024 级
第一次月考数学试题
(总分:150 分 考试时间:120 分钟)
第I卷(选择题共58分)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选
项中,只有一项是符合题目要求的.
1. , 若 ,则实数 为( )
A. B. C. D.
2.复数 = ,则 为( )
A. B. C. D.
3.下列函数中,最小正周期为 ,且在 上单调递减的是( )
A. B. C. D.
4. 在 中, ,则最大角余弦值为
( )
A. B. C. D.
5.向量 、 满足: , , ,则 在 上的投影向
量的模为( )
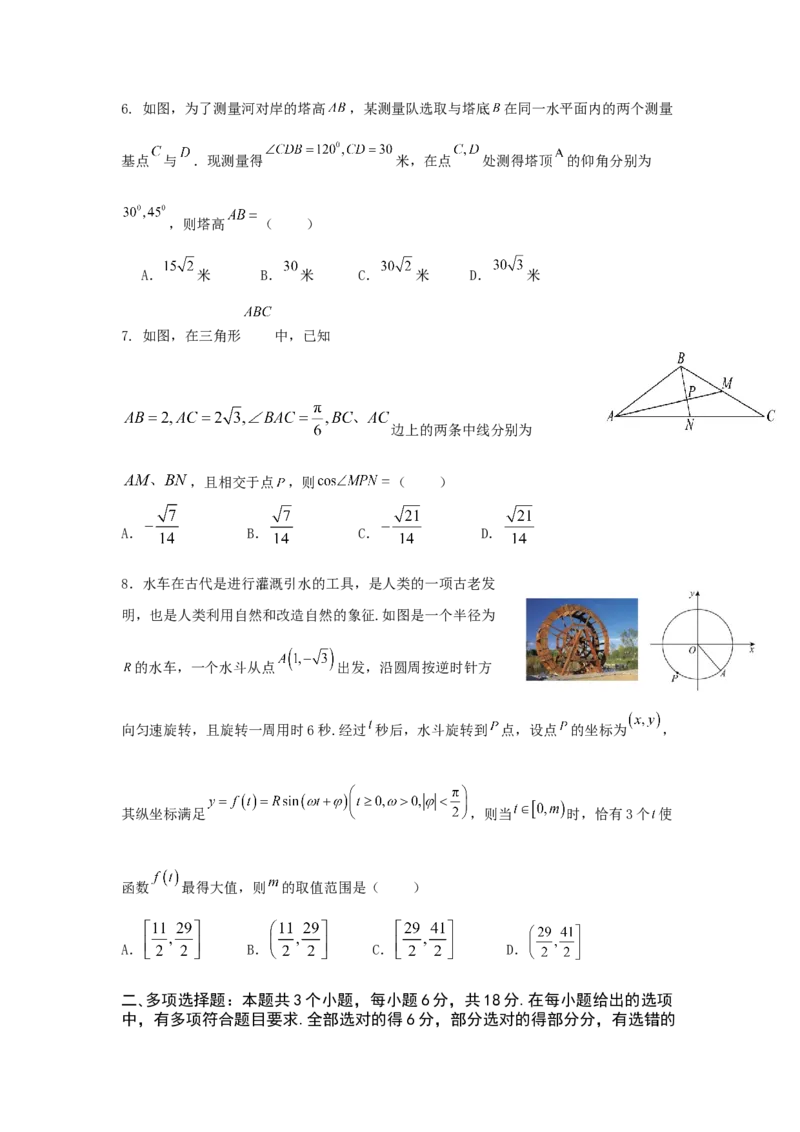
A. B. C. D.6. 如图,为了测量河对岸的塔高 ,某测量队选取与塔底 在同一水平面内的两个测量
基点 与 .现测量得 米,在点 处测得塔顶 的仰角分别为
,则塔高 ( )
A. 米 B. 米 C. 米 D. 米
7. 如图,在三角形 中,已知
边上的两条中线分别为
,且相交于点 ,则 ( )
A. B. C. D.
8.水车在古代是进行灌溉引水的工具,是人类的一项古老发
明,也是人类利用自然和改造自然的象征.如图是一个半径为
的水车,一个水斗从点 出发,沿圆周按逆时针方
向匀速旋转,且旋转一周用时6秒.经过 秒后,水斗旋转到 点,设点 的坐标为 ,
其纵坐标满足 ,则当 时,恰有3个 使
函数 最得大值,则 的取值范围是( )
A. B. C. D.
二、多项选择题:本题共3个小题,每小题6分,共18分.在每小题给出的选项
中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.复数 , , 的共轭复数为 ,则下列结论正确的是( )
A.若 为纯虚数,则
B.若 在复平面内对应的点位于第四象限,则
C.若 ,则
D.若 ,则
10.已知函数 , ,则( )
A.函数 的最小正周期为
B.函数 关于 对称
C.函数 的值域为
D.函数 在 上是减函数
11. 在 中, , , 为 边上及内部的一动点,设
,则下列说法正确的是( )
A.若 为 的重心,则
B.若 为 的外心,则
C.若 为 的内心, ,则
D.若 为 的垂心, 为锐角三角形,则 与 共线
第II卷(非选择题共92分)
三、填空题:本题共3小题,每小题5分,共15分.12. 将函数 的图像向左或者向右平移 个单位,图像关于原点对
称,求 的最小值 .
13. 在 中,内角A,B,C所对的边分别为 ,已知 ,且
,则 外接圆面积为 .
14. 正方形 的边长为3, 是线段 上靠近 的三等分点, 是线段 (含端
点)上的动点, 为线段 的中点,则 的最小值为 .
四、解答题:共5个小题,满分77分.其中15题13分,16,17题分别15分,
18,19题分别17分,解答应写出相应的文字说明,证明过程或演算步骤.
15.已知函数
(1)求 的最小正周期和对称轴;
(2)判断函数 在 的单调性.
16. 已知向量 满足 ,且 .
(1) 求 , ;
(2)若向量 与 的夹角为锐角,求实数 的取值范围.
17. 在锐角 中,角A,B,C的对边分别是 且
.
(1)求角 的大小;
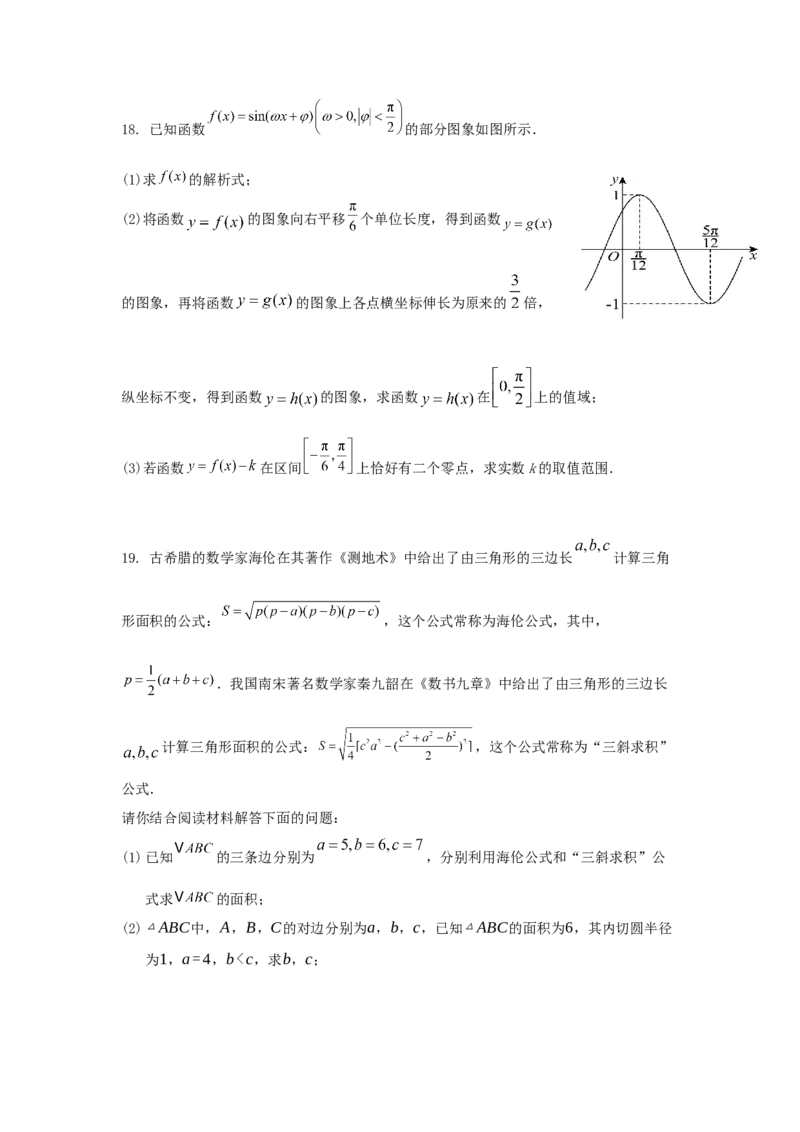
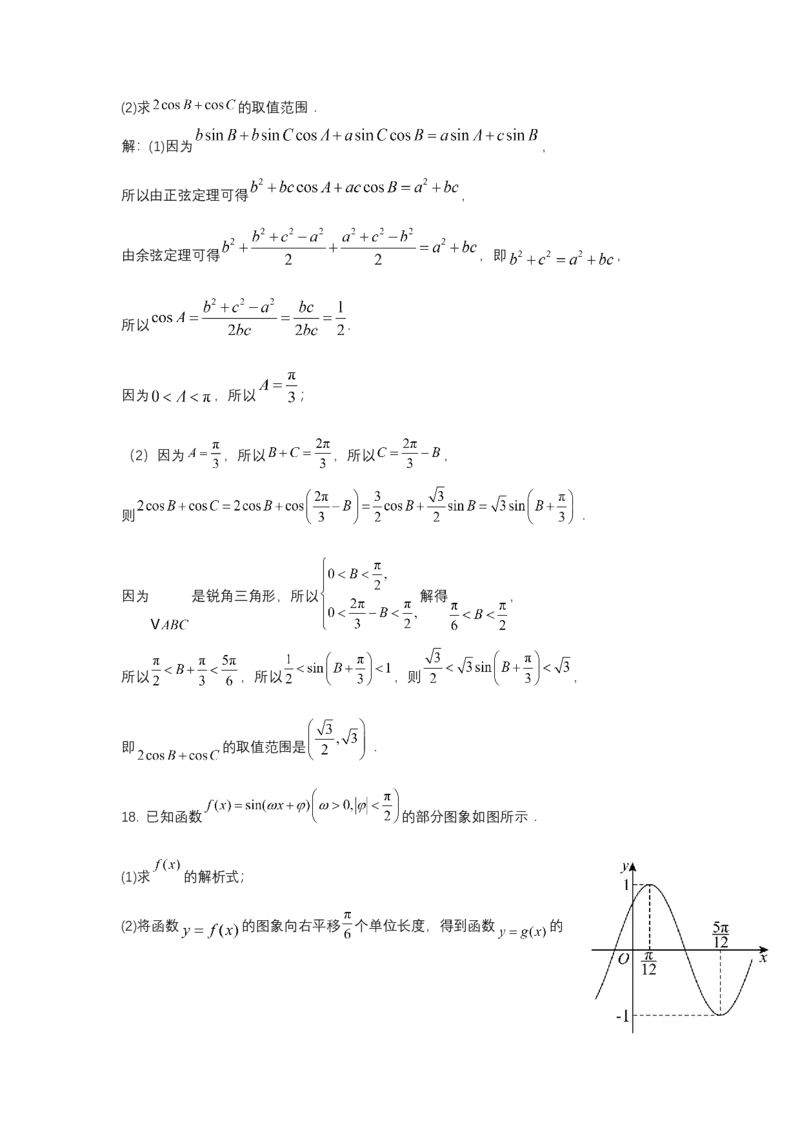
(2)求 的取值范围.18. 已知函数 的部分图象如图所示.
(1)求 的解析式;
(2)将函数 的图象向右平移 个单位长度,得到函数
的图象,再将函数 的图象上各点横坐标伸长为原来的 倍,
纵坐标不变,得到函数 的图象,求函数 在 上的值域;
(3)若函数 在区间 上恰好有二个零点,求实数k的取值范围.
19. 古希腊的数学家海伦在其著作《测地术》中给出了由三角形的三边长 计算三角
形面积的公式: ,这个公式常称为海伦公式,其中,
.我国南宋著名数学家秦九韶在《数书九章》中给出了由三角形的三边长
计算三角形面积的公式: ,这个公式常称为“三斜求积”
公式.
请你结合阅读材料解答下面的问题:
(1)已知 的三条边分别为 ,分别利用海伦公式和“三斜求积”公
式求 的面积;
(2)△ABC中,A,B,C的对边分别为a,b,c,已知△ABC的面积为6,其内切圆半径
为1,a=4,b